基于改进麻雀搜索算法的变电构架优化方法
张迎春, 姜 岚, 唐 波, 陈 曦, 胡 辉
(1.三峡大学 电气与新能源学院,湖北 宜昌 443002; 2.湖北省输电线路工程技术研究中心,湖北 宜昌 443002;3.国网湖北省电力有限公司经济技术研究院,武汉 430000; 4.智方设计股份有限公司,武汉 430000)
近年来,随着新型电力系统概念的提出,输变电工程结构的安全性与可靠性也被广泛关注。由于供电需求的逐步提升与输变电技术的不断发展,高压、特高压输电工程已经成为电网建设的重点。变电站构架是输变电工程中非常重要的工程结构,主要承受导线张力和各种环境荷载。随着电压等级的提升,变电构架承受的荷载更复杂,结构高度、跨度的提高导致用钢量也越来越大。因此,在保证结构稳定性与安全性的前提下,能够通过优化设计减少钢材用量,使得结构更加经济与环保具有重要意义。
将变电构架的三角形格构式梁视为空间桁架结构进行优化分析,目前,桁架结构的优化类型主要分为尺寸优化、形状优化、拓扑优化三种[1-2],所涉及的优化方法主要有最优准则法、数学规划法以及智能优化方法三大类[3-4]。其中,最优准则法对于单约束的优化问题更加有效,难以适应多种形态的约束;数学规划法是一种精确的求解方法,但对于多变量大型复杂结构的优化设计,其计算量过大,通用性差;而智能优化算法近年来发展迅速,遗传算法、粒子群算法、鲸鱼优化算法等被相继提出,因该类算法有着鲁棒性强、通用性好且易于与其他算法相结合等优点[5-6],所以其在结构优化设计方面有着较为广泛的应用。麻雀搜索算法(sparrow search algorithm, SSA)由Xue等[7]于2020年提出,作为一种新型群体智能优化算法,它的优化思想主要来源于麻雀种群的觅食行为和反捕食行为。该算法能够处理连续型以及离散型设计变量,且无需计算灵敏度,对约束条件也没有特殊要求。根据其在测试函数中的结果表明,与粒子群算法、灰狼优化算法等相比,该算法的鲁棒性更强,收敛速度更快,有望在结构优化领域发挥重要作用。
本文在基本麻雀搜索算法的基础上加入Circle混沌映射以及萤火虫扰动策略,对其易陷入局部最优解,收敛速度慢[8]等缺点进行改进,而后建立桁架结构的尺寸优化模型,并将改进麻雀搜索算法(improved sparrow search algorithm, ISSA)用于典型桁架结构以及变电构架的尺寸优化研究,结果表明了该算法在结构优化设计中的有效性。
1 麻雀搜索算法及改进
1.1 麻雀搜索算法
根据麻雀群体的觅食行为及反捕食行为,可以将麻雀种群抽象为探索者-跟随者-预警者模型。其中,探索者在种群中的能量储备最高,具有较好的适应度值,它们为整个种群提供觅食的方向;跟随者会密切关注探索者,从而获得更好的食物来源,以增加自身的适应度值;预警者会在遇到危险时发出警报,此时,处于种群边缘的麻雀会移动到安全区域,处于中间位置的麻雀则会随机游走,靠近其他麻雀[9]。
将SSA用于优化问题,若在D维搜索空间中存在着N只麻雀,则第i只麻雀在空间中的位置为Xi=[xi1,…,xid,…,xiD],相对应的适应度值为Fx=[f(xi1),…,f(xid),…,f(xiD)],其中,i=1,2,…,N,表示种群中的麻雀个数;d=1,2,…,D,表示待优化问题的设计变量维数。
在SSA中,探索者有着更广泛的搜索范围,因此会在搜索过程中优先获得食物来源,在每次的迭代过程中,探索者的位置更新描述如下
(1)
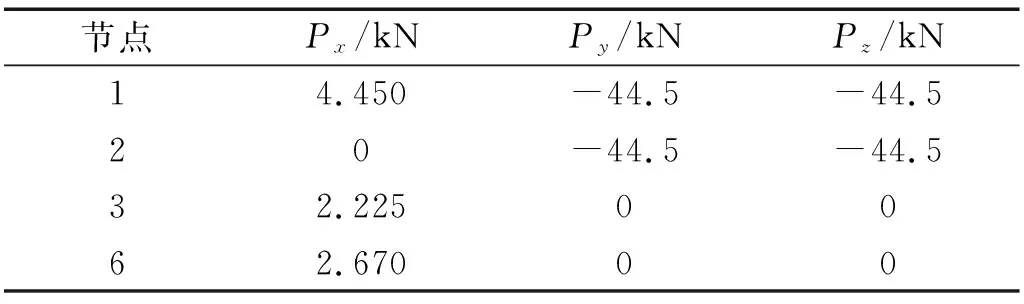
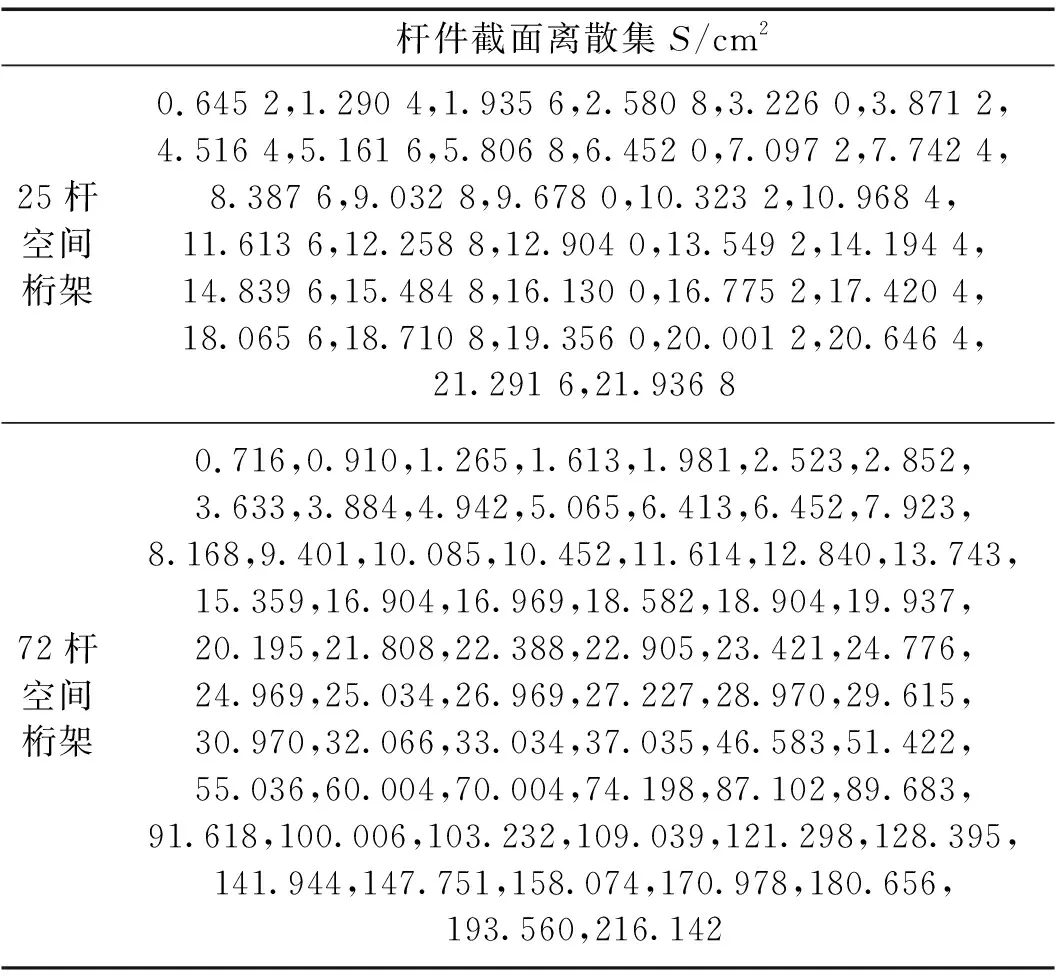
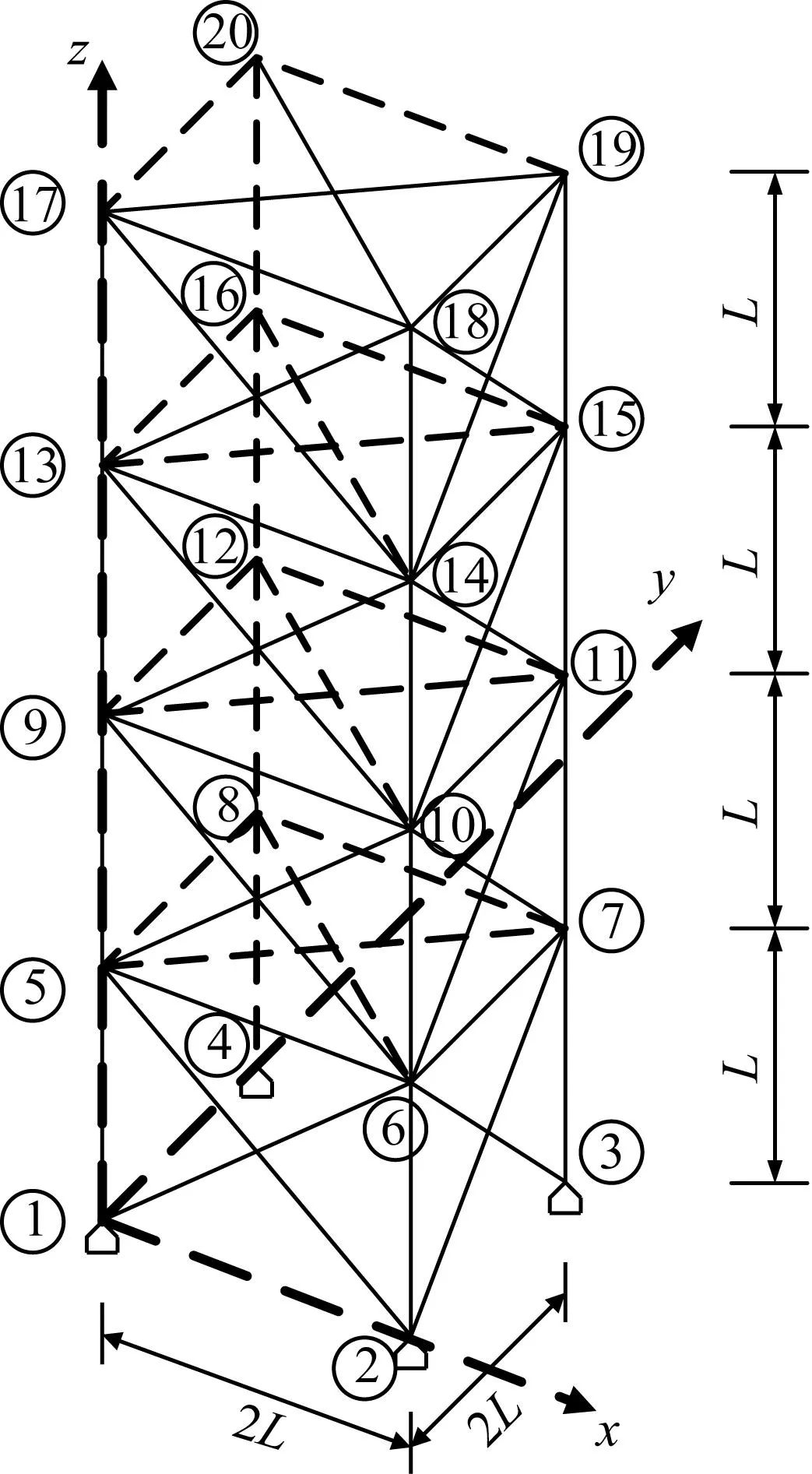
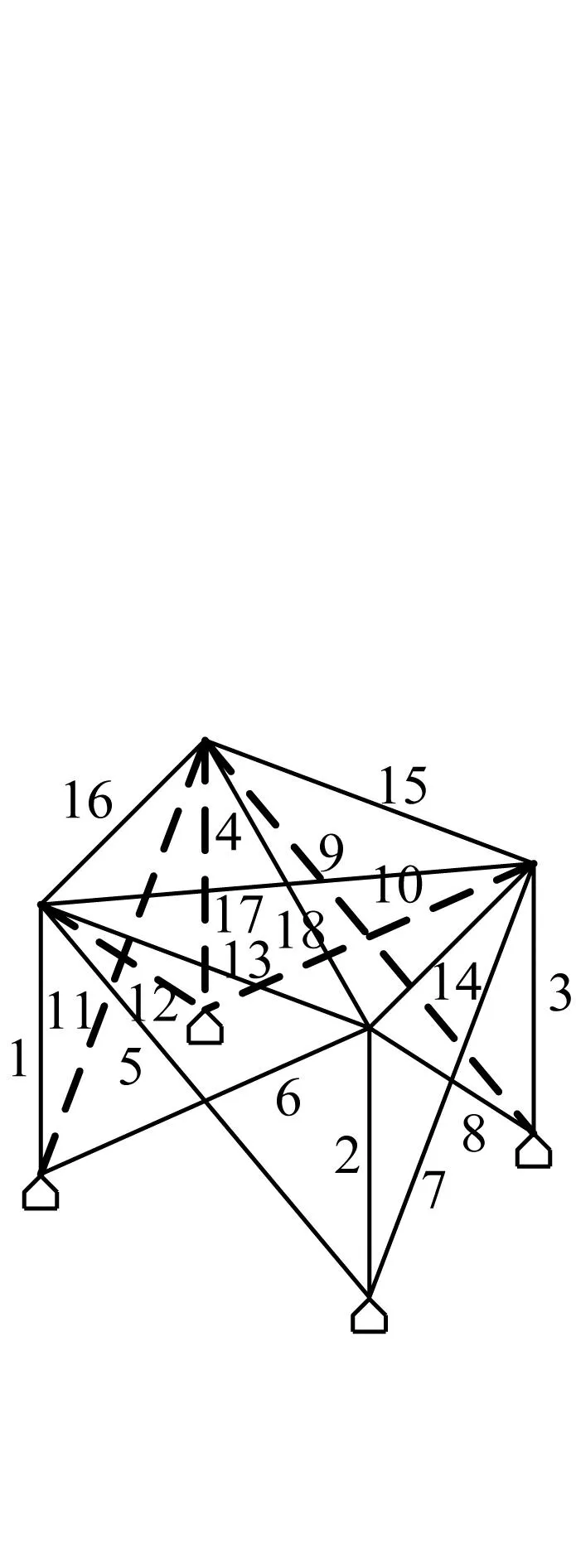
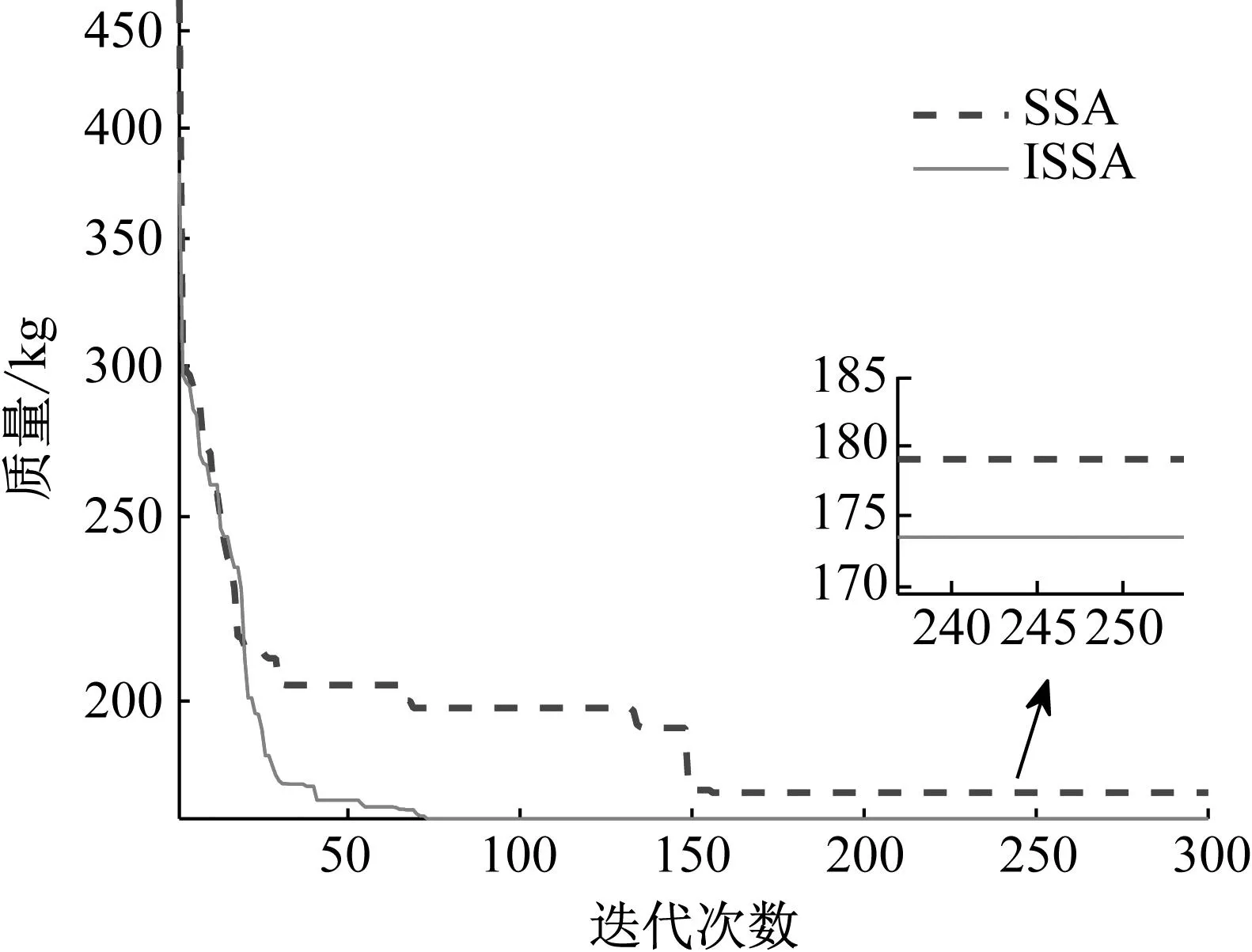
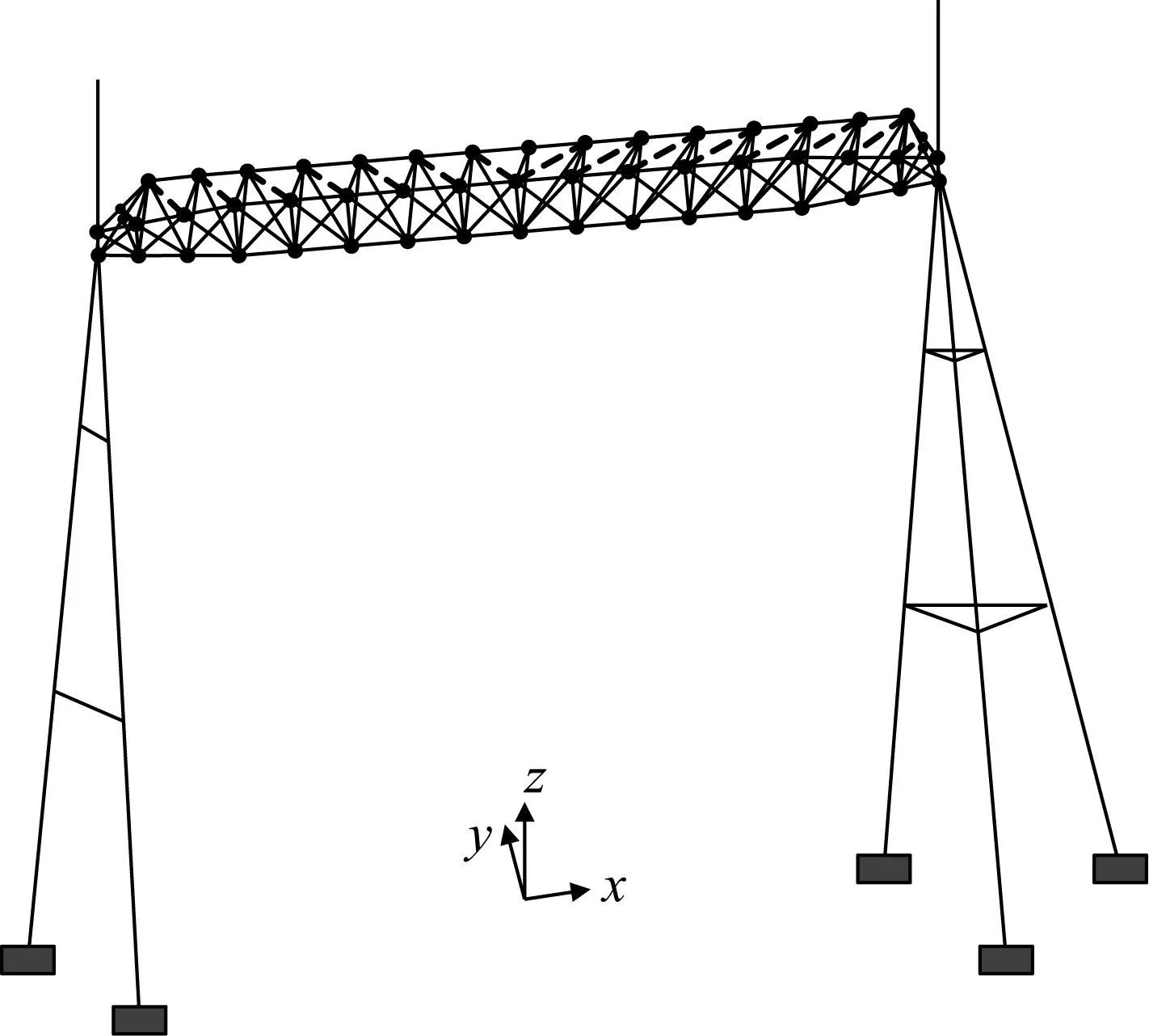
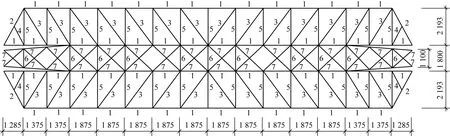
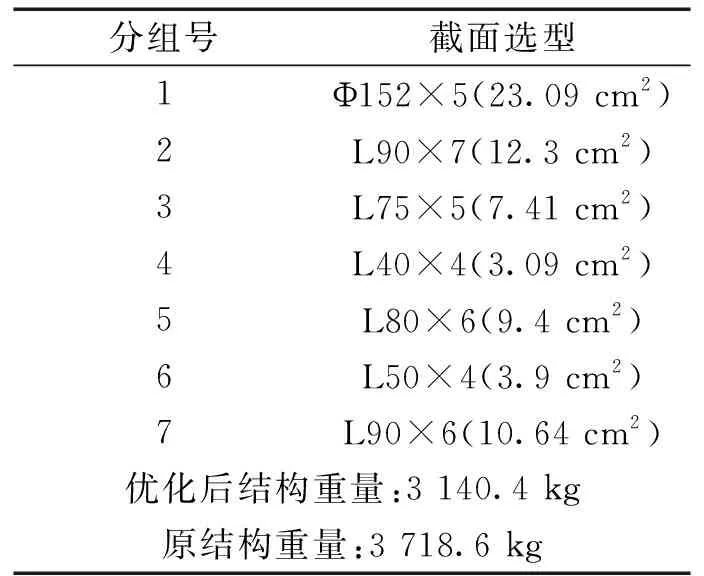
式中:t为当前的迭代次数;itermax为最大的迭代次数;α∈(0,1]随机取值;Q为服从正态分布的随机数;L为元素全为1的1×d矩阵;R2∈[0,1]为预警值;ST∈[0.5,1]为安全值。当R2 种群中除了探索者以外,其余麻雀均为跟随者,迭代过程中,跟随者的位置更新描述如下 (2) 式中:xworst为当前种群中的全局最差位置;xp为当前发现者的最优位置;A+=AT(AAT)-1,A为1×d矩阵,矩阵中的每个元素被随机赋值为1或-1。当i>N/2时,表明第i个跟随者没有获得食物,适应度值较低,需迫切飞往他处觅食;当i≤N/2时,表明第i个跟随者将在最优位置附近觅食。 在种群中随机挑选麻雀作为预警者,其数量一般占种群的10%~20%,预警者的位置更新描述如下 (3) 式中:xbest为当前全局的最优位置;β为步长控制参数,服从正态分布(均值为0,方差为1);K∈[-1,1]随机取值;fi、fw、fg分别为当前麻雀个体适应度值、当前全局最差适应度值及最佳适应度值;ε为防止分母为零的极小常数。当fi>fg时,表明麻雀处于种群边缘,易被捕食者攻击;当fi=fg时,表示处于种群中间位置的麻雀意识到了危险,需向其他麻雀靠近以躲避攻击。 针对基本麻雀搜索算法在优化时易陷入局部极值,收敛速度慢等缺点,对其进行改进。因混沌作为一种普遍存在的非线性现象,具有遍历性、随机性等特点[10-11],所以在原算法的基础上加入Circle混沌映射,使算法的初始值分布更加均匀,增加种群的多样性,提升算法的收敛性;为避免SSA陷入局部最优解,对所有麻雀更新后的位置进行萤火虫扰动,以提高其寻优精度。 1.2.1 Circle混沌映射 由于基本麻雀搜索算法在生成初始种群时具有随机性,所以会出现聚集等分布不均的情况,使得其在整个解空间中的覆盖率不高,不利于算法的广泛搜索,所以许多学者会引入混沌映射来解决此类问题。鉴于Circle混沌映射的覆盖率较高且比较稳定,所以本文在初始种群生成时采用Circle混沌映射以增加种群的多样性,使其分布更加均匀。 Circle混沌映射的表达式如下 (4) 式中:i+1表示解的维度数。当维度为500时,Circle混沌映射初始解的维度分布图与直方图分别如图1和图2所示。由图1和2可知,Circle映射的混沌值在[0,1]之间的分布较均匀。 图1 Circle混沌映射分布图Fig.1 Circle chaotic map distribution 图2 Circle混沌映射直方图Fig.2 Circle chaotic map histogram 1.2.2 萤火虫扰动策略 萤火虫算法(firefly algorithm, FA)是由Yang[12]于2008年提出的一种元启发式算法。萤火虫主要通过发光来实现求偶或者觅食的目的,因此该算法模拟了萤火虫的发光特性,将搜索与优化过程模拟为萤火虫的吸引与移动过程。本文针对基本麻雀搜索算法易陷入局部最优的问题,在算法最后引入了萤火虫扰动策略,对麻雀个体的位置进行扰动更新,将扰动后的适应度值与扰动前的值进行对比,若适应度值更优,则进行位置更新。萤火虫的吸引度描述如下 (5) 式中:β0为最大吸引度;γ为光强吸收系数;ri,j为萤火虫i与j之间的距离。 萤火虫i被萤火虫j吸引并向其移动的位置更新描述如下 xi=xi+β*(xj-xi)+α*(rand-1/2) (6) 式中:xi和xj分别为萤火虫i和j所处的空间位置;α∈[0,1]为步长因子。 本文对于变电构架梁的尺寸优化设计,主要以结构质量最轻为目标函数,以杆件的横截面积为设计变量,且取离散值,以杆件的应力,长细比以及节点的位移为约束条件,由此建立的优化设计数学模型描述如下。 以结构质量最轻建立的目标函数为 (7) 式中:W为结构的总质量;Ai∈S为杆件的截面面积;S={S1,S2,…,SNS}为可选用的杆件截面离散集;ρi与li分别为第i根杆件的材料密度和单元长度;n为结构中的杆件数量。 考虑的约束条件主要如下: (1) 杆件的应力约束 (8) (2) 杆件的长细比约束 (9) (3) 节点的位移约束 uj-[u]≤0 (10) 式中:σi为第i根杆件的应力;f为钢材的强度设计值;φi为轴心受压构件的稳定系数;λi为第i根杆件的长细比;[λ]C与[λ]T分别为杆件受压以及受拉的许用长细比;uj为第j个节点的位移值;[u]为节点的许用位移值。 对于变电构架梁的优化设计,属于有约束的优化问题,相比于无约束优化,有约束优化使得可行域变小,搜索空间也更加复杂,因此会增大求解难度。对于有约束的优化问题,目前主要有罚函数法、可行性法则、随机排序法等约束处理方法,其中罚函数法是最为常用的处理方法之一[13-15],在求最小值的优化问题中,其原理可简单解释为,对不满足约束条件的解赋予一个较大的值,故在寻找最小值的优化过程中,此解将会被排除在外。本文将采用罚函数法来处理杆件的应力,长细比以及节点的位移这些约束条件,此方法是对原来的目标函数增加惩罚项,从而将约束优化问题转换为无约束优化问题来处理,故最终建立的目标函数如下所示 (11) 在对桁架结构进行优化设计时,主要采用有限单元法作为结构分析方法。有限元法主要分为离散化、单元分析以及整体分析三部分,对于桁架结构,可将杆件视为单元,在MATLAB中编制桁架结构的内力分析程序,可求得单元刚度矩阵、结构的整体刚度矩阵,进而得出节点位移以及单元内力等结果,用于分析判断是否满足约束条件。 结合尺寸优化设计的数学模型,采用改进麻雀搜索算法进行尺寸优化设计的流程如图3所示。 图3 尺寸优化设计流程Fig.3 Size optimization design process 为方便与其他优化算法进行对比分析,算例选用两种广泛用于结构优化设计,以验证各优化算法是否有效的空间桁架结构,即25杆及72杆空间桁架结构。其中,前者形似输电铁塔结构,共10个节点,25根杆件;后者为四层塔架结构,共20个节点,72根杆件。分别将改进前后的算法用于两种桁架结构的尺寸优化分析。 25杆空间桁架结构的节点编号及尺寸信息如图4所示。结构中杆件的弹性模量E=6.895×1010Pa,密度ρ=2 768.8 kg/m3,许用应力为2.759×108Pa,节点在x、y、z方向上的许用位移为0.889 cm。本例将桁架结构的25根杆件分为8组,分组信息如表1所示,结构的荷载工况如表2所示,杆件截面的离散集S如表3所示。 图4 25杆空间桁架(cm)Fig.4 25 bar space truss (cm) 表1 结构杆件连接及分组Tab.1 Connection and grouping of structural members 表2 荷载工况Tab.2 Load case 表3 杆件截面离散集Tab.3 Discrete set of member section 72杆空间桁架结构的节点编号及尺寸信息如图5所示。其中,L=152.4 cm。结构中杆件的弹性模量E=6.895×1010Pa,许用应力为1.724×108Pa,密度ρ=2 768.8 kg/m3,结构顶部四个节点在x、y、z方向上的许用位移为0.635 cm。根据对称性,将桁架结构的72根杆件分为16组,分组号如表4所示,结构的荷载工况如表5所示,杆件截面的离散集S见表3。 图5 72杆空间桁架Fig.5 72 bar space truss 表4 杆件分组Tab.4 Bar grouping 表5 荷载工况Tab.5 Load case 将SSA与ISSA分别用于25杆及72杆空间桁架结构的尺寸优化设计,其中,算法所涉及的参数值设置如下:种群数量N=50,最大迭代次数itermax(25杆)=200,itermax(72杆)=300,探索者占种群数量的20%,其余为跟随者,预警者占种群数量的20%,安全值ST=0.8,最大吸引度β0=1,光强吸收系数γ=1,步长因子α=0.2。 将基本麻雀搜索算法及改进麻雀搜索算法分别独立运行20次,并将结果与现有文献进行对比。两种空间桁架结构的优化结果分别如表6和表7所示,算法改进前后的收敛曲线分别如图6和图7所示。 表6 25杆空间桁架优化结果Tab.6 Optimization results of 25 bar space truss 表7 72杆空间桁架优化结果Tab.7 Optimization results of 72 bar space truss 图7 72杆空间桁架优化收敛曲线Fig.7 Convergence curve of 72 bar space truss optimization 对于25杆空间桁架结构的尺寸优化,由表6可知,ISSA的最优值与文献[16-18]相比虽只减少了约0.1%,但其平均值及标准差明显小于其他文献算法,表明ISSA更加稳定,鲁棒性更强,这主要由于加入了萤火虫扰动策略,使算法易于跳出局部极值,具有更强的稳定性。ISSA的最优值与SSA相比虽相差不大,但同样其平均值及标准差明显更小,且由图6可知,改进后的算法迭代不到30次就找到了最优解,而基本麻雀搜索算法迭代将近50次才趋于收敛,可见,改进后的算法收敛速度更快,这主要由于加入了Circle混沌映射,使得初始值分布更加均匀,增加了其靠近最优解的概率,以至提升了算法的收敛速度。 对于72杆空间桁架结构的尺寸优化,由表7结果可知,ISSA的最优值相比于文献[19-21]及SSA的最优值,分别减少了8.8%、0.9%、0.2%及3.1%。与SSA相比,ISSA有着更小的平均值及标准差。其中,与文献[21]相比,ISSA的优化效果虽不明显,但文献[21]中所提算法在优化时迭代将近200次才得到最优解,而由图7可知,ISSA迭代70次左右就找到了最优解,可见,ISSA的收敛速度明显更快。 将改进麻雀搜索算法用于某500 kV变电构架梁的尺寸优化设计,其中,变电构架高26 m,构架梁为三相挂点,跨度为27 m,地线柱高8 m,构架梁上下弦杆均采用钢管,其余构件采用角钢,横梁高为2 m,宽为1.8 m,到端部变为1.1 m,变电构架整体模型如图8所示。构架采用Q235钢,钢材的强度设计值f=2.15×108Pa,还应考虑相应的折减系数,具体参考DL/T 5457—2012 《变电站建筑结构设计技术规程》[22],弹性模量E=2.06×1011Pa,质量密度ρ=7 850 kg/m3。构架梁跨中的挠度限值为梁总跨度的1/300,横梁上下弦杆及立面支座角钢的许用长细比为150,其余杆件的许用长细比为200。 图8 变电构架模型Fig.8 Model of substation structure 将构架梁中的杆件分为7组,具体分组信息在展开式构架梁中表示,如图9所示。 图9 杆件分组(mm)Fig.9 Bar grouping (mm) 杆件截面离散集S={L40×4(3.09 cm2),L45×4(3.49 cm2),L40×5(3.79 cm2),L50×4(3.9 cm2),L56×4(4.39 cm2),L50×5(4.8 cm2),L56×5(5.42 cm2),L63×5(6.14 cm2),L70×5(6.88 cm2),L63×6(7.29 cm2),L75×5(7.41 cm2),L80×5(7.91 cm2),L70×6(8.16 cm2),L75×6(8.8 cm2),L80×6(9.4 cm2),L75×7(10.16 cm2),L90×6(10.64 cm2),L80×7(10.86 cm2),L90×7(12.3 cm2),L90×8(13.94 cm2),Φ146×5(22.15 cm2),Φ152×5(23.09 cm2),Φ159×5(24.19 cm2),Φ152×5.5(25.31 cm2),Φ146×6(26.39 cm2)},其中,前20个用于角钢选型,其余用于钢管选型。 此变电构架主要考虑最严重覆冰、最大风速、最低气温、单相上人、三相上人以及单相紧线六种工况,但由变电构架的资料可知,最低气温、三相上人和单相紧线三种工况下的荷载组合不起控制作用,所以在受力分析时主要考虑另外三种工况下的荷载组合。所分析的荷载主要包括:结构自重、风荷载(顺导线方向以及垂直导线方向)、导线张力,其中,最大风速工况下,风速v=28 m/s,最严重覆冰及单相上人工况下,风速v=10 m/s,垂直于结构表面的风荷载标准值计算公式如下 Wk=βzμsμzW0 (12) 式中:Wk为风荷载标准值(kN/m2);βz为高度z处的风振系数;μs为风荷载体型系数;μz为风压高度变化系数;W0为基本风压(kN/m2)。 在三种工况下对变电构架梁进行优化设计,其中,算法最大迭代次数itermax=300,其余算法参数设置同算例分析。优化结果及收敛曲线分别如表8和图10所示。 表8 变电构架梁优化结果Tab.8 Optimization results of substation structure beam 图10 构架梁优化收敛曲线Fig.10 Optimization convergence curve of structure beam 由以上结果可知,采用改进麻雀搜索算法对变电构架梁进行尺寸优化设计,优化率约为15.5%。当取得最优值时,结构中杆件所受最大拉应力为159 MPa,最大压应力为-126 MPa,均小于许用应力值;结构中弦杆及立面支座角钢的最大长细比为137,小于150,其余杆件的最大长细比为192,小于200;构架梁跨中的最大位移值为0.026 m,小于许用位移值。由此可知,改进后算法能够在保证结构稳定性与安全性的前提下,提高其经济性。 本文主要对基本麻雀搜索算法做出改进,并建立了桁架结构的尺寸优化模型,结合结构分析的有限元法,将改进麻雀搜索算法分别用于经典桁架结构以及变电构架的尺寸优化设计,得到的主要结论如下: (1) 针对麻雀搜索算法易陷入局部最优及收敛速度慢的缺点进行改进,分别引入Circle混沌映射及萤火虫扰动,增强了算法的鲁棒性,提升了算法的收敛速度。 (2) 改进麻雀搜索算法在算例分析中,与文献及基本麻雀搜索算法相比,其优化效果均有提升,稳定性及收敛速度明显提高。 (3) 将改进麻雀搜索算法用于实际工程中变电构架梁的优化设计,改进后算法对于变电构架梁的优化率约为15%,表明其适用于工程中的初步设计阶段,具有实用价值。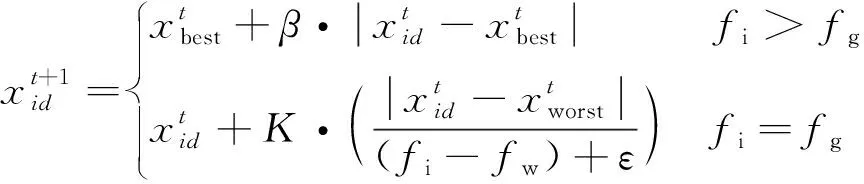
1.2 改进麻雀搜索算法
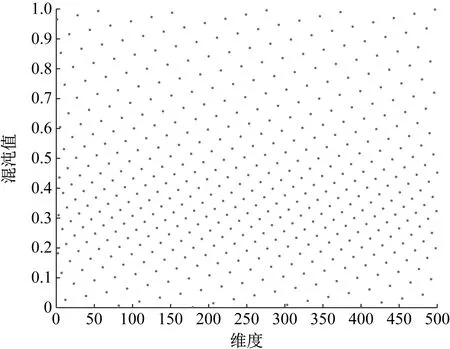
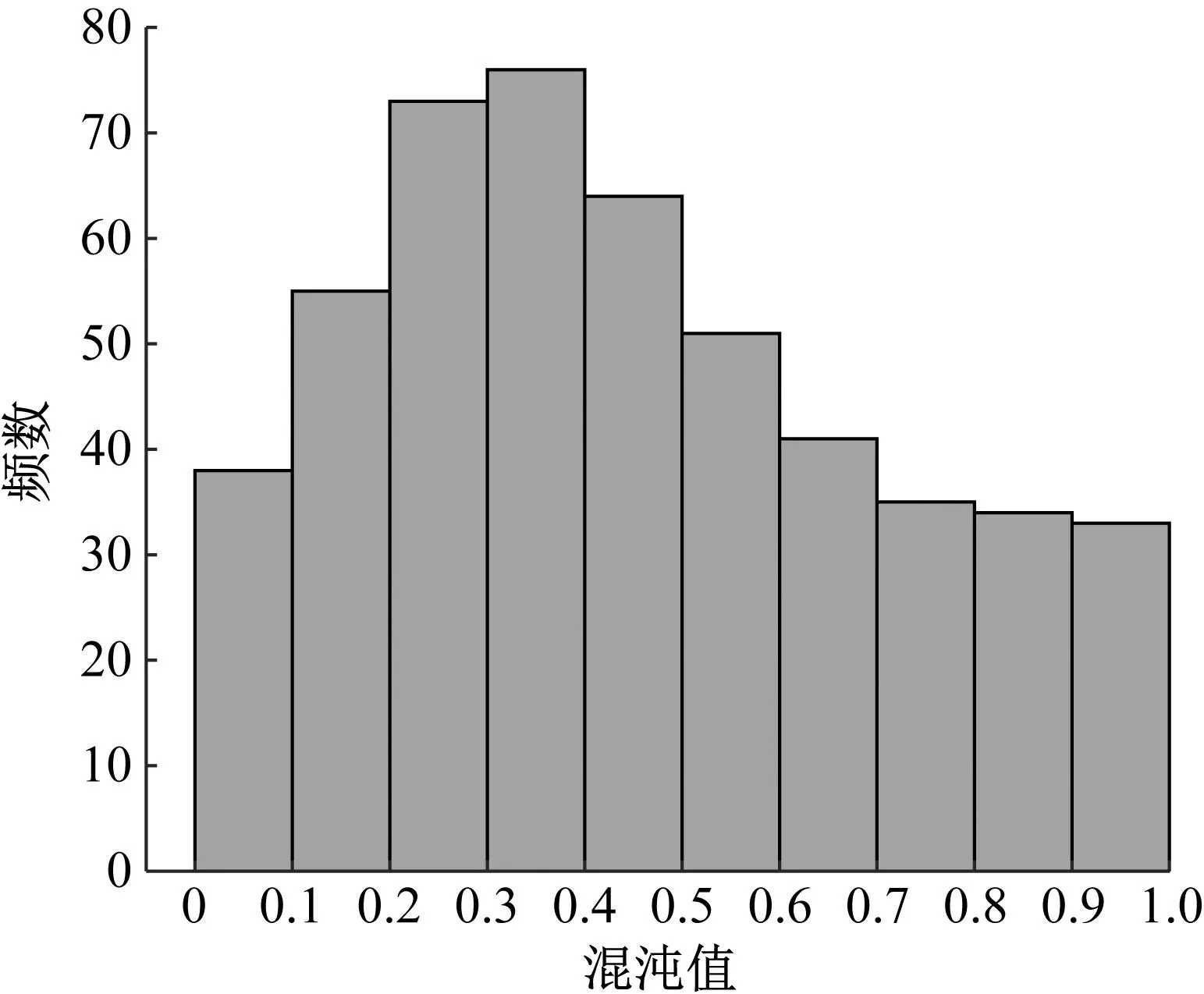
2 尺寸优化模型及优化流程
2.1 尺寸优化模型
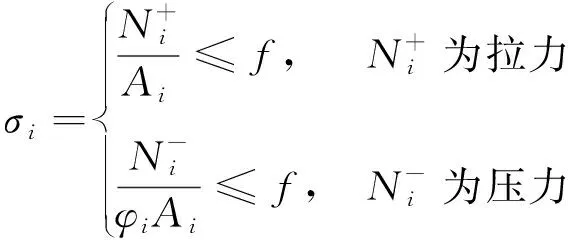
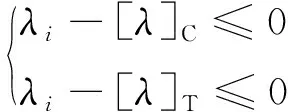
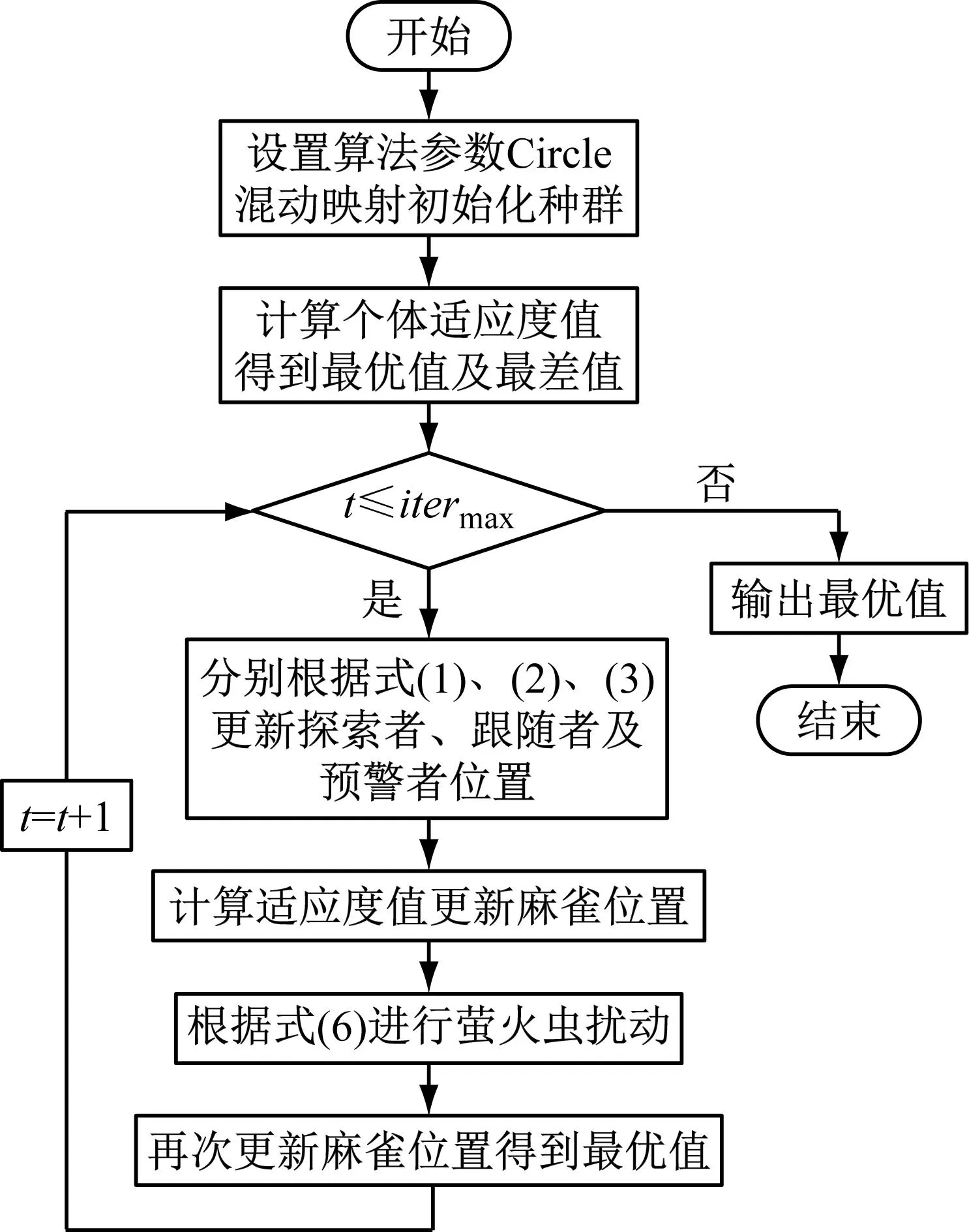
2.2 优化流程
3 算例分析
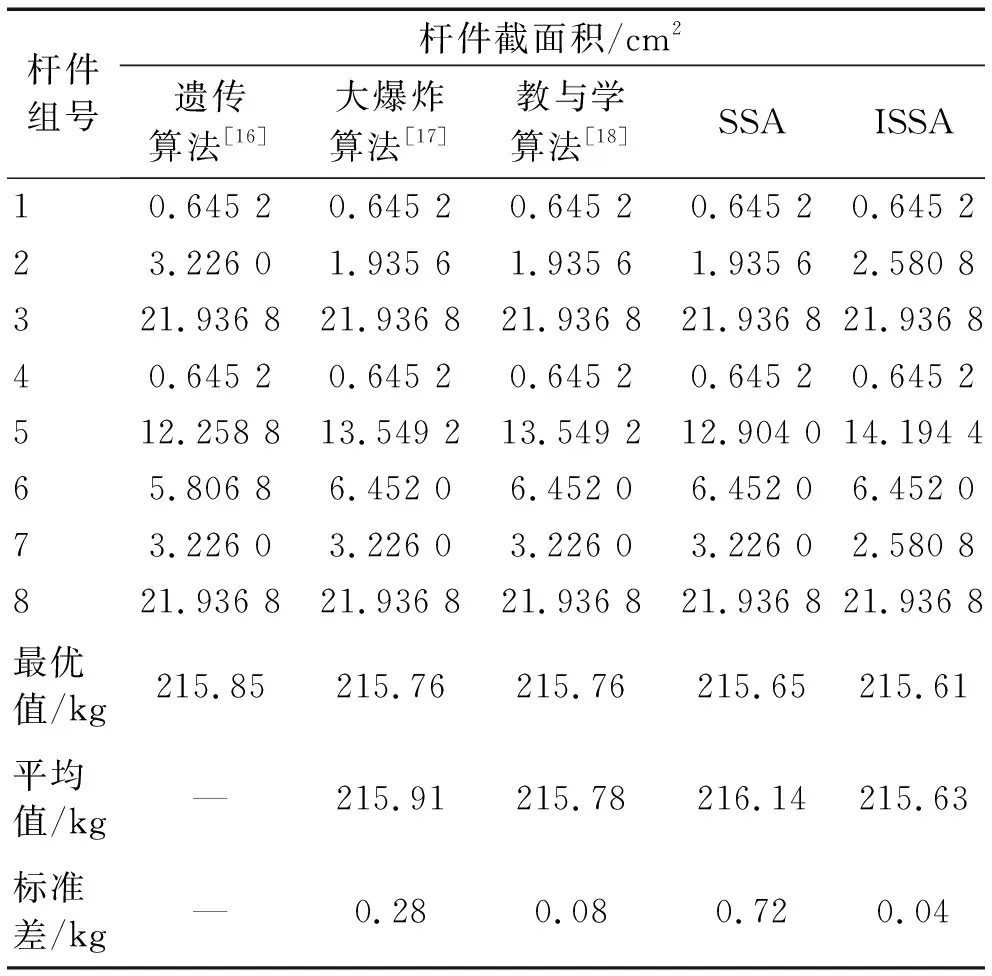
3.1 25杆空间桁架结构
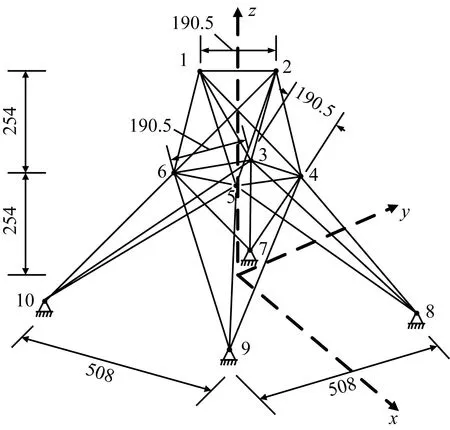
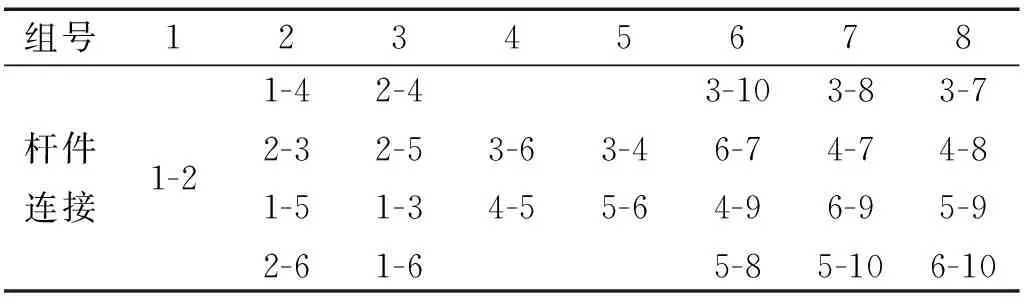
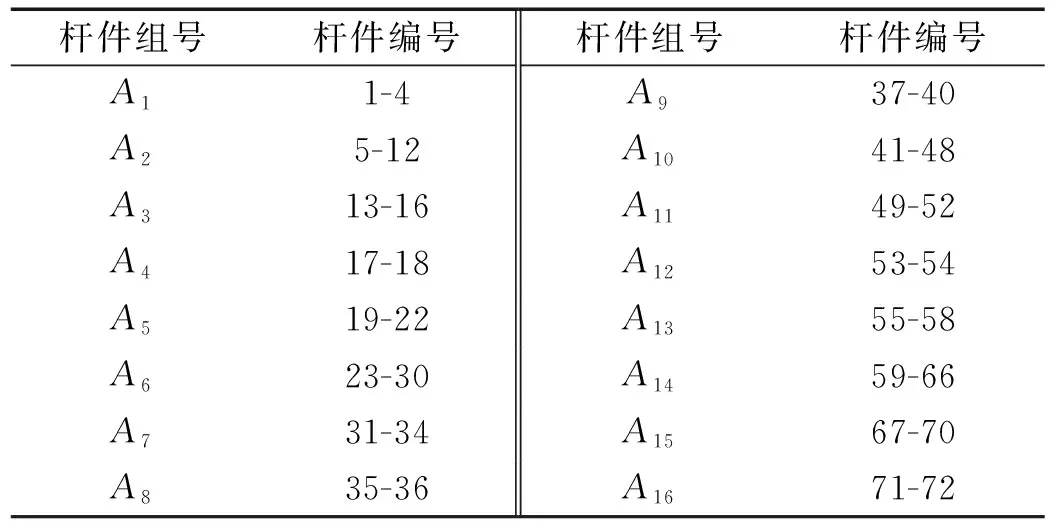
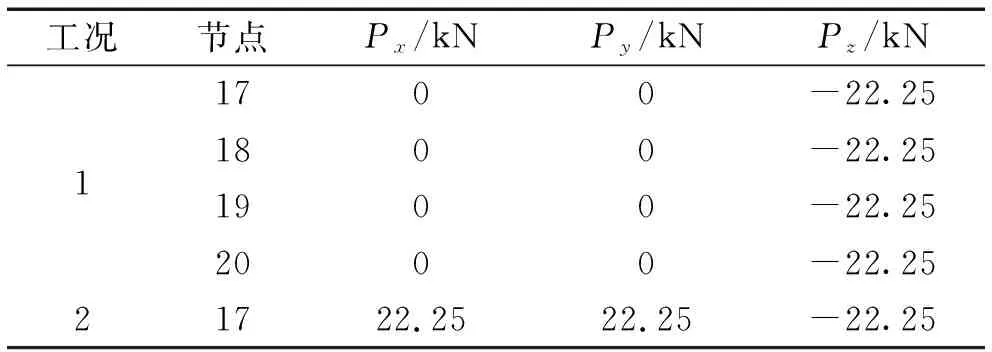
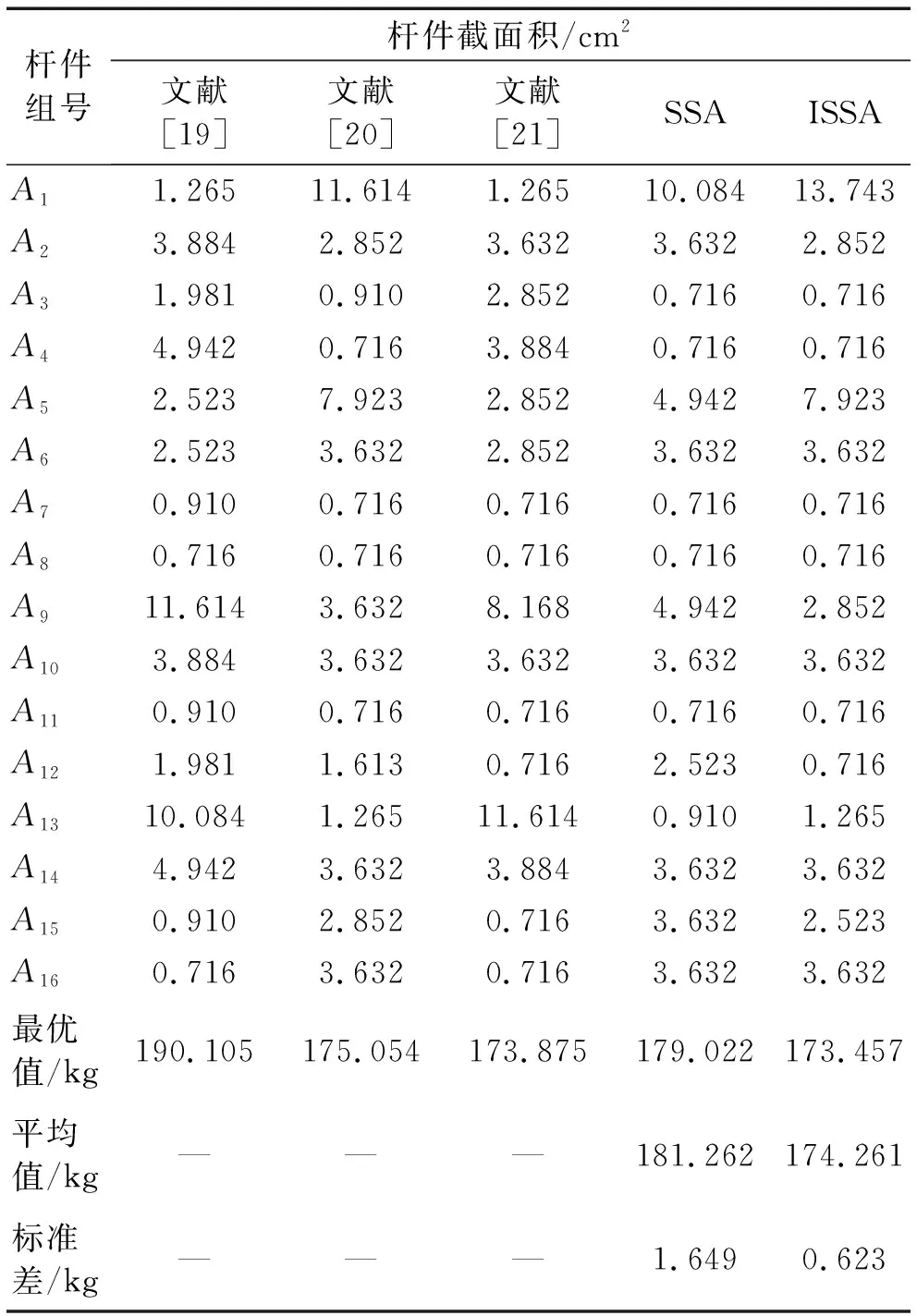
3.2 72杆空间桁架结构
4 工程应用

5 结 论

