京津冀生产性服务业集聚对经济增长的空间溢出效应

李茹，徐琼

（信阳学院数学与统计学院，河南 信阳 464000）

1 研究现状

随着世界经济进入服务经济时代，作为现代服务业主要表现形式的生产性服务业在经济领域的地位越来越不容忽视。2015 年国家提出京津冀协同发展战略，京津冀地区成为引领我国经济发展的核心城市群，具有先进的知识技术及更多的人才资源，能够更好地发挥自身的示范和辐射作用，促进周边地区产业协同发展。探究京津冀地区生产性服务业集聚对经济增长的空间溢出效应，可以更好地推动京津冀一体化发展，引领国家经济发展。

1988 年SCOTT 首次提出“服务业集聚”的概念[1]。自此，越来越多的学者开始对生产性服务业集聚的经济效应进行研究。豆建民和刘叶[2]通过构建阈值回归模型，发现服务业与制造业的协同集聚对城市经济增长具有双重门槛效应。王晶晶和李灵玉[3]采用空间计量模型进行分析，发现产业协同集聚与经济高质量发展具有显著的空间相关性。西爱琴等[4]构建门槛面板模型研究发现创新型生产性服务业创业协同对经济增长有显著的促进效应，但也容易受到拥挤效应的影响。赵景华等[5]以京津冀城市群为研究对象进行分析，发现生产性服务业与制造业形成空间集聚的基本动因是他们之间的供需关系，因此应充分发挥生产性服务业的空间辐射效应。李俊杰和王雪颜[6]采用系统广义矩估计（GMM）方法进行研究，发现京津冀地区不同产业的集聚效应和拥塞效应对经济高质量发展的影响存在差异。

综上所述，很多学者从理论及实证方面对生产性服务业集聚和经济增长的关系进行了探究，但是对二者之间的空间效应研究较少，而对京津冀地区的研究多从理论分析出发，忽略了生产性服务业对经济增长的空间溢出效应。鉴于此，本文对京津冀生产性服务业集聚对经济增长的空间效应进行探究。

2 模型构建

2.1 模型设定

空间杜宾模型（SDM）是空间滞后模型与空间误差模型的一般形式，其基本形式为：

Yit=ρWYit+βXit+WXitθ+εit

其中，Yit为被解释变量，ρ 为空间自相关系数，W 为空间权重矩阵，Xit为解释变量，β 为解释变量系数，εit是独立同分布的随机误差项，θ 表示解释变量对被解释变量的空间相关系数。如果满足条件H1∶θ=0，空间杜宾模型可以简化为空间滞后模型，如果满足条件H2∶θ+ρβ=0，空间杜宾模型可以简化为空间误差模型。

2.2 变量测度与数据说明

选取京津冀地区13 个地级市2008-2020 年相关数据，数据来源于《中国统计年鉴》《中国城市统计年鉴》，个别缺失的数据采用插值法予以补齐。运用Matlab 软件进行建模和分析。

变量详细指标测度如下：

①被解释变量：以人均生产总值（PGDP）测度经济发展水平。

②核心解释变量：生产性服务业集聚指标（LQ），用区位熵表示，其计算公式为：

其中，Eis表示城市i 生产性服务行业s 的单位从业人数，Ei表示城市i 全部单位从业人员数。

③其他控制变量：劳动力供给（L）用市辖区年末单位从业人员数表示；物质资本投入（K）用地区当期固定资产投资额表示；政府干预（Igov）用财政收入占市辖区GDP 比重表示；城市规模（POP）用市辖区年末总人口数衡量；外商直接投资（FDI）用年末外商直接投资额表示。

3 实证分析

3.1 权重矩阵的构建与空间自相关检验

为充分刻画京津冀经济增长空间单元之间的关联性，本文构造了如下两个权重矩阵：

W1：0-1 权重矩阵，如果两个地级市之间有共同的边界，元素记为1，否则为0。

W2：地理距离权重矩阵，用dij表示用经纬度计算的地级市i 和j 之间的欧式距离，当i≠j 时，元素为，否则记为0。

空间自相关检验采用莫兰指数（Moran'I），其计算公式为：

其中，n 代表样本总区域数，xi和xj表示在i 地区和j 地区的样本观测值，代表样本观测值的均值，Wij表示权重矩阵中度量i 地区和j 地区关联程度的元素，S2表示方差。

计算两种权重矩阵下京津冀地区2008-2020 年经济增长的莫兰指数，结果如表1 所示。

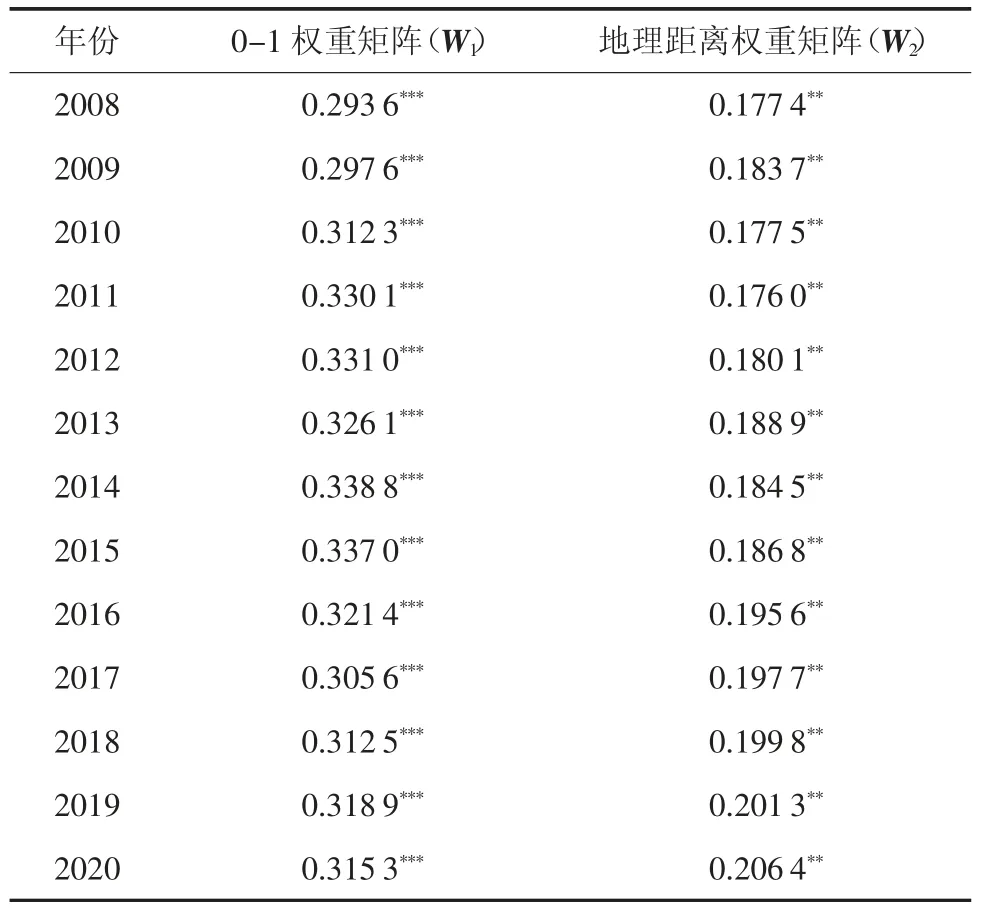
表1 京津冀地区经济增长的莫兰指数

由表1 可知，在两种权重矩阵下，经济增长的莫兰指数均为正，且在0-1 权重矩阵下通过了1%的显著性水平，在地理距离权重矩阵下通过了5%的显著性水平。可以发现，京津冀各地市经济增长之间存在较强的空间联动性，可以建立空间计量模型。

3.2 模型选择

在进行实证分析之前，首先应该检验所研究内容适合哪种空间模型，由于地理距离权重矩阵更具一般性，因此在地理距离权重矩阵下进行判断。

第一步，检验空间计量模型适合固定效应还是随机效应，进行Hausman 检验，Hausman 检验统计量为（78.643 5，p=0.000 0），拒绝原假设，表明模型更加适合固定效应。

第二步，判断适合哪种空间计量模型，检验结果如表2所示，空间滞后模型和空间误差模型均在1%的显著性水平上通过了LM 检验和R-LM 检验，接下来考虑是否适合空间杜宾模型。

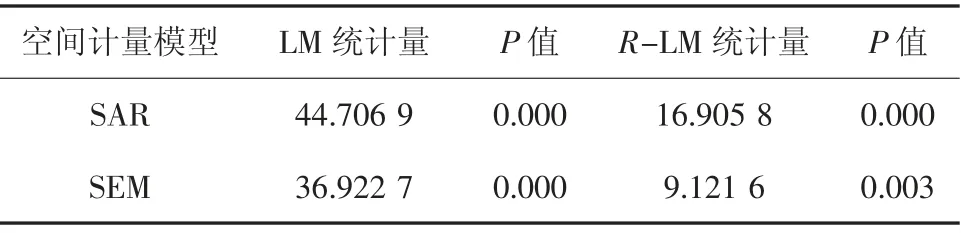
表2 空间计量模型的LM 和R-LM 检验

第三步，判断空间杜宾模型是否可以简化为空间滞后模型或空间误差模型，所得结果均在1%的显著性水平下拒绝了原假设。因此，空间杜宾模型更加适合本研究。最终表明采用空间杜宾模型的固定效应较为合适。

3.3 结果分析

为消除面板数据的异方差，将所有变量取对数后进行实证分析，0-1 权重矩阵下与地理距离权重矩阵下模型回归结果基本一致，本文仅列出地理距离权重矩阵下回归结果，结果如表3 所示。

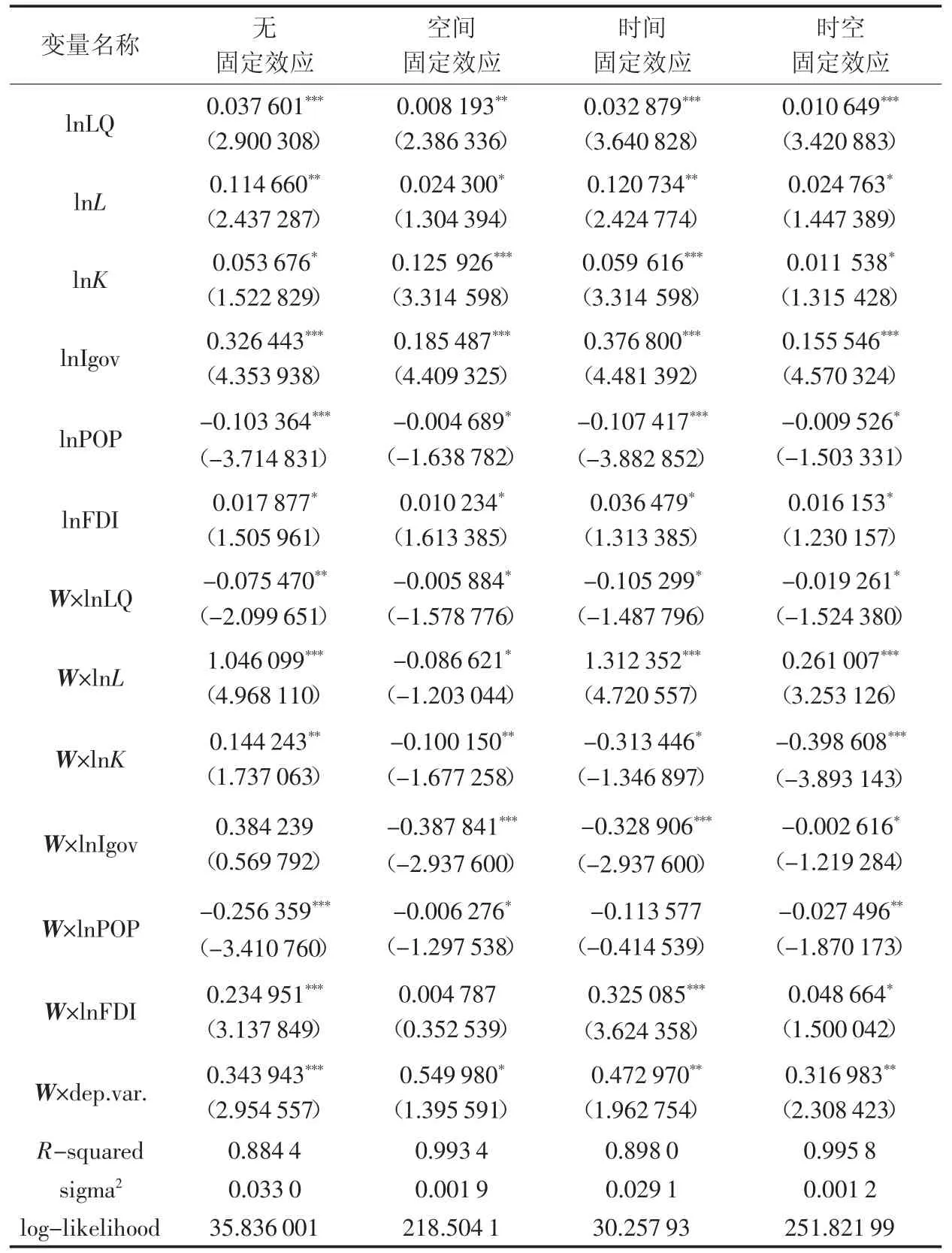
表3 空间杜宾模型回归结果

由表3 结果可得，京津冀地区的经济增长具有较强的外溢效应，邻近地区的经济增长对本地区的经济增长具有显著的正向影响。无论在哪种固定效应下，生产性服务业集聚对京津冀经济增长都具有显著的正相关作用，说明生产性服务业集聚能够显著促进本地区经济增长，但是空间系数显著为负，即邻近地区的生产性服务业对本地区的经济增长具有显著的阻碍作用。地理距离构建的权重矩阵对经济增长影响因素衡量更为严格，即不相邻地区距离越小，影响程度越大。同时物质资本投入、政府干预程度对本地区经济增长具有显著促进作用，而对外地区经济增长具有显著阻碍作用。劳动力供给、外商直接投资对本地和外地的经济增长均具有显著的正向影响，而政府规模对本地和外地的经济增长存在显著的负向作用。

为进一步分析各因素对经济增长的影响效应，依据LeSage 和Pace[7]提出的方法，分解权重矩阵下的直接效应和间接效应，结果如表4 所示。

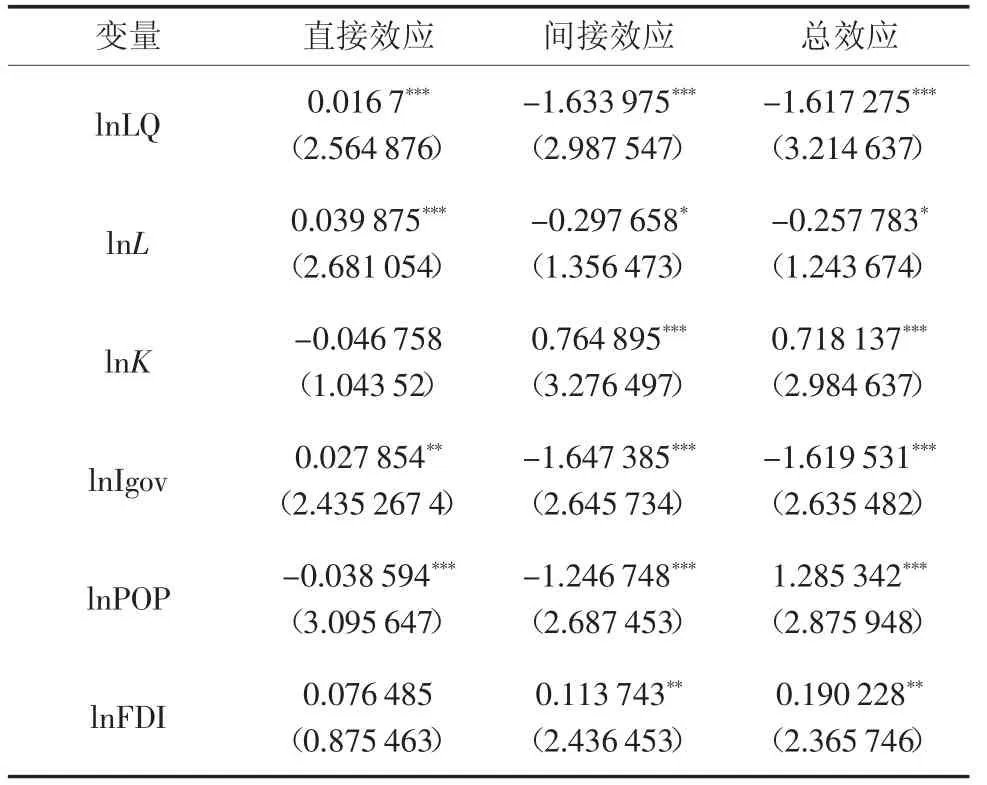
表4 生产性服务业对京津冀经济增长的直接效应和间接效应

结果表明，生产性服务业集聚的直接效应显著，且系数为0.016 7，说明与实证结果相似，生产性服务业集聚能够促进本地经济增长，而其间接效应显著为负，说明本地区的生产性服务业集聚阻碍了邻近地区的经济增长。

4 结论

采用空间杜宾模型实证分析京津冀生产性服务业集聚对经济增长的影响，结果表明：京津冀地区生产性服务业空间集聚特征显著，区域经济增长存在明显的空间溢出效应；生产性服务业集聚对本地区的经济增长具有显著的促进作用，而对邻近地区经济增长具有显著的阻碍作用，且随着两个地区之间距离的缩小，阻碍作用逐渐增大；劳动力供给、外商直接投资对本地和外地经济增长均具有显著正向影响，物质资本投入和政府干预程度对本地经济增长具有显著的促进作用，而对外地经济增长具有显著的负向作用，城市规模对本地和外地经济增长均具有负向影响。