基于层间垫平的囊匣三维装箱优化设计

李国志，李莹欣，雒波波，刘迪，谭思可，李文凤

基于层间垫平的囊匣三维装箱优化设计

李国志1a,b，李莹欣1a,b，雒波波2，刘迪1a,b，谭思可1a,b，李文凤1c*

（1.陕西科技大学 a.中国轻工业功能印刷与运输包装重点实验室 b.轻化工程国家级实验教学示范中心 c.设计与艺术学院，西安 710021；2.秦始皇帝陵博物院，西安 710600）

为提高囊匣的装载率及装箱效率，研究层间垫平的强异构类的三维装箱问题，实现快速计算囊匣装箱方案和衬垫方案并指示装箱。基于囊匣实际装箱需求，以衬垫体积最小为目标，设计基于贪心策略与改进的装箱顺序策略的两步优化启发式算法，对装箱与衬垫方案进行优化；并根据不同放置方向，设计不同的输出效果以指示装箱。与装箱优化前数据进行对比实验证明，该算法推荐的装箱方案与衬垫方案可以减少木箱的使用数量与体积，减少垫平用衬垫体积7.21%，装箱时间缩短了约一半。文中设计的混合启发式算法能为囊匣装箱问题找到合适的装箱与衬垫方案，减少衬垫的使用，提高装载率以及装箱效率。

囊匣；三维装箱；衬垫生成；贪心策略；启发式算法

文物与艺术品是人类艺术的瑰宝，传承文化，沟通中外。在它们储存、运输中通常使用定制囊匣作为包装，一物一盒，尺寸多样[1]。随着文化事业的发展，文物展出、艺术品交易等活动日益增多，不可避免地面临着更多的搬运、储存、运输等情况。目前的囊匣装箱往往依靠人工经验重复试装，无法保证装载率与装载效率，且目前对三维装箱的研究，没有与囊匣装箱场景相匹配的装箱软件去计算装箱方案。因此，研究该场景下的装箱问题，设计装箱算法，对推动文物、艺术品的智能装箱、智能管理具有重要意义。

装箱问题是典型的NP-Hard问题，无法求得精准的解。按照维度可以将其分为一维、二维、三维装箱问题[2]。国内外学者对装箱优化问题进行了深入的研究，取得了一定的研究成果。目前的研究问题有在线装箱[3]、多尺寸容器的装载[4]、基于现实多种约束的装箱系统开发[5]等。大多研究者通过结合构造性启发式算法与元启发式算法来解决装箱问题。常见的元启发式算法有模拟退火算法（SA）[6]、遗传算法（GA）[7]、蚁群算法（AC）[8]、禁忌搜索算法（TS）[9]、大规模邻域搜索算法[10]等，强化学习算法[11]也应用于装箱问题求解中。构造性启发式算法有基于块装载[12]、基于层装载、深度优先搜索等的三维装箱启发式算法，有基于左下、最低水平线、最低水平线搜索等的二维装箱启发式算法。不过，由于每种算法都有它特定的一个前提条件，这就使得在面对各种复杂的约束时，这些算法的应用场景就会具有局限性。

本文基于囊匣层间垫平的装箱场景，以使用衬垫体积最小为优化目标建立数学模型，求解优化囊匣装箱方案及衬垫方案，主要从以下3点解决该问题：一是设计基于贪心策略的启发式算法，将目标问题分解为2步进行优化求解；二是设计一种启发式的基于装箱经验的装箱序列的生成算法，使寻优更高效；三是设计装箱方案与衬垫方案的输出效果，有效指示装箱。

1 囊匣装箱问题分析

囊匣是从库房货架上搬运装至木箱中再装入车厢开始运输。本文研究的是囊匣的第1次集装，即从货架到木箱中的装箱过程。

囊匣的组成与结构由其内装物的特性决定。由于文物、艺术品的特性，囊匣由内囊和外匣组成，根据内装物重量的不同，外匣的制作材料有瓦楞纸板、胶合板等，内囊的材料有棉花、聚氨酯泡沫等[13]。为了在搬运、储存、运输中很好地保护文物与艺术品，囊匣尺寸要很好地贴合其内装物，因此囊匣多量身定做，尺寸非常丰富[14]。

囊匣由于内装物的独特性，其装箱区别于其他装箱问题，有独特的装箱要求。在囊匣装箱中，EPE衬垫可以有效避免震动、碰撞、相对滑移等，从而很好地保护囊匣。具体装箱过程是一层囊匣装满后，剩余的空隙处用EPE衬垫补满，高度凹凸不平的层间用EPE衬垫垫平，每层重复直至木箱装满。在这一过程中，工人依靠人工经验，多次重复搬运试装以找到合适的装箱方案，并现场测量空隙，切割制作衬垫。重复的搬运工作既不利于囊匣的保护，也浪费了时间人力；现场测量切割衬垫不利于装箱工作的连续性，无法保证时效；且装载方案耗费EPE衬垫多，囊匣装载率不高。

2 模型建立

2.1 问题描述

已知囊匣数量为，长宽高分别为l,w, h（=1～），共种木箱可供选择，长宽设定为高度为H（=1～）。寻找最优的装箱方案，选用合适的木箱，将个囊匣全部装进木箱中，使装载时使用的EPE衬垫体积最小，囊匣的装载率最高，并输出装箱与衬垫方案。

囊匣设计制作时综合考虑了内装物、开口方式、取放等因素，因此在储存运输时，不能倒置，仅可平放，即囊匣装箱时有2种放置方向可供选择，如图1所示。

图1 囊匣的2种放置方向

2.2 研究假设

基于现实装箱条件，为了便于求解，本文做出如下假设：囊匣与木箱内腔均为规则长方体；单个囊匣的长宽高均小于木箱的长宽高；囊匣挤压产生的微小形变忽略不计；囊匣的质量均匀，重心位于中下部[15]；囊匣仅可平放，不能翻转，能水平旋转90°；囊匣具有一定的承载力，可叠放，摆放层数不限。

2.3 目标函数与约束条件

建立三维直角坐标系，以-平面为底面，垂直于轴。平行于木箱长建立轴，平行于木箱宽建立轴，平行于木箱高建立轴。用参数0和1区别囊匣是否旋转，囊匣的旋转参数R为0时，代表囊匣的长平行于木箱长放置。当旋转参数R为1时，代表囊匣的长平行于木箱的宽放置。

1）大樱桃秋季施肥有利于树体养分储备，对树体抗寒、抗旱、抗病、抗衰老、抑制冒条等有明显效果。应重视秋季施肥，把握好施肥时间，为来年开花、结果、丰产打下基础。一般在8—9月进行早秋施基肥，施肥后当年就能发挥肥效，增加树体营养积累，有利于来年开花结果。施肥量应占到全年施肥总量的70%以上。

如图2所示，设置合适的数据结构记录各层囊匣以及衬垫的位置，以第层为例，第个囊匣的最终放置坐标为（a, b, c, d），其中（a, b）是囊匣左下角坐标，（c, d）是囊匣右上角坐标。对应衬垫坐标为（a, b, h, c, d, h），（a, b, h）为左下角坐标，（c, d, h）为右上角坐标，其中h为囊匣的高度，h表示第层最高的囊匣高度加上基础的衬垫厚度。

图2 囊匣与衬垫坐标

确定约束条件如下：

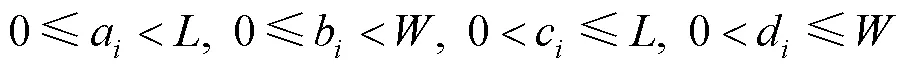
c–a=l,d–b=w或c–a=w,d–b=l(2)

其中，式（1）约束了囊匣的左下角及右上角坐标在木箱尺寸允许范围之内；式（2）～式（3）约束了囊匣仅可旋转，不可倒置；式（4）～式（5）约束了旋转参数为0时，囊匣的长平行于木箱长，旋转参数为1时，囊匣的长平行于木箱宽；式（6）约束了囊匣的总装载高度小于所选木箱的总高度。

3 启发式算法设计

启发式算法不能保证装箱问题的最优解，但是它能给出装箱场景下一个合适的解。传统启发式算法可以求得问题的近似解而非最优解，相比于精确算法，不再局限于求解小规模装箱问题，其应用范围更广。

3.1 求解策略

3.1.1 贪心策略

本文采用贪心策略，通过保留每步中最优的结果，求得原问题的最优解。分析装箱要求与装箱目标，可知影响装箱效果的关键要素是高度，本文将衬垫体积最小这一优化目标分解为2步进行优化求解。第1步优化求解中假设木箱高度无限高，将囊匣装箱，求得装载高度最低的方案作为最优解保留；第2步选用合适的木箱使得装载率最大，将第1步最优解方案中高度确定的各层囊匣分入各木箱中。第2步所选用木箱及第1步中各层的装箱方案与衬垫方案即为整体方案的最优解。

3.1.2 装箱顺序策略

装箱序列即从1到的排列。基于现实装箱经验，在装箱时先装体积大的囊匣，后装体积小的囊匣会更容易找到合适的装箱方案。为了达到装载高度最低、衬垫体积最小的要求，分析可知高度相差在较小范围内的囊匣放在同一层可以有效减小衬垫的体积。因此，本文对初始装箱序列做出如下优化设计：第1步对要装入木箱的囊匣先按照高度进行降序排列，高度相同则按照囊匣底面积降序排列；第2步将第1步生成的囊匣序列，以每10个囊匣为一组，按照底面积降序排列，生成初始装箱序列。该设计可以使初始序列更合理，寻优更高效。

3.2 模型求解

3.2.1 第1步优化求解

模拟退火算法（Simulated Annealing，SA）是一种通用的优化算法，其出发点是基于物理中固体物质的退火过程与一般的组合优化问题之间的相似性。其中Metropolis准则是SA算法收敛于全局最优解的关键所在，Metropolis准则以一定的概率接受非最优解，这样就使算法跳离局部最优的陷阱。

在第1步优化问题中，本文设计了模拟退火[16]结合最低水平线算法来求解装箱高度最低的方案，将三维装箱问题转换为多层的二维装箱问题。算法流程图如图3所示。

图3 第1步优化算法流程

3.2.2 第2步优化求解

将第1步的最优解中各层囊匣分别装入各个木箱中使装载率最大。大多数情况下最后一层剩余空间较大，为了避免这一层被放入底层或中间层，约束最后一层囊匣只能放入某个木箱的顶层。算法流程如图4所示。其中，使用模拟退火算法求解单个木箱的最优层序列，具体步骤为初始化参数，初始层序列为从1到，层高从高到低，对层序列做随机扰动，迭代计算出最优层序列。

3.2.3 参数确定

模拟退火算法能得到较为合适且高效的排样方案，但是得到合理的参数需要一定的时间和装箱实验。模拟退火算法中，初始温度越高，温度衰减系数越接近于1，马尔科夫链越长，模拟退火搜索越充分，越有可能找到全局的最优解。相应地，搜索时间也会越长。

囊匣数量不同，设定的参数也不同。采用定量对比研究法来确定第1步优化求解中模拟退火算法的参数，综合考虑计算时长与是否寻找到最优解，参数确定如表1所示。

图4 第2步优化算法流程

表1 第1步优化求解中参数

Tab.1 Parameters in the first step optimization solution

第2步优化求解问题规模较小，计算较快，参数设置为初始温度1为1 000 ℃，终止温度2为1 ℃，降温速率取值为0.9，马尔科夫链长取值为200。

4 实例验证与分析

4.1 输出结果与运行

对程序运行输出结果进行设计。为了提高装箱效率，输出方案简洁明了，方便识别与装箱。按照木箱一箱一图，输出各箱中各层的装箱及对应的衬垫方案。设计装箱方案为二维图形展示，每个长方形对应一个囊匣，左下角辅以编号，便于指示装箱；并根据不同的放置方向，用不同颜色线条加以区分，长平行于木箱长的囊匣用红色线条表示，宽平行于木箱长的囊匣用蓝色线条表示，有助于装箱时摆放正确，提高装箱效率。衬垫方案为三维效果，衬垫尺寸可直观显示，便于提前切割制作。

为验证囊匣三维装箱算法的适用性和输出效果，以200个囊匣装箱为例进行运行试验。导入200个囊匣的长宽高数据，设定木箱长宽高，计算装箱方案，运行结果如图5所示。图5是木箱的使用数量，图6是具体的装箱方案与衬垫方案，表2为木箱尺寸选择与最终装箱高度。

图5 200个囊匣的整体装箱方案

图6 200个囊匣的具体装箱方案

表2 木箱选择与装箱高度

Tab.2 Selection of wooden cases and packing height

运行试验证明，文中算法有较好的运算能力与输出效果。

4.2 对比试验

为了验证囊匣三维装箱的优化效果，文中选取了某公司20次历史装箱数据来进行模拟实验，该公司木箱共有4种尺寸可选，如表3所示。

表3 可选木箱编号与尺寸

长宽为1 200 mm×1 000 mm，高度分别为600、1 200、1 000、2 000 mm，分别编号为1、2、3、4号箱。实验数据如表4所示可知，本文该程序取得了较好的效果，实现了囊匣装箱方案的优化。如表4所示，为运输公司调研及具体试验数据。

表4 优化结果与原数据的对比

Tab.4 Comparison between optimized results and original data

表4中，空间利用率指木箱中囊匣与衬垫体积之和占木箱体积的比率，衬垫节省率指用于垫平的EPE衬垫体积的节省率。分析表4中数据可知，该设计可以为囊匣装箱推荐更合适的箱型，减少木箱的使用数量与体积，垫平用衬垫体积可减少7.21%，时间上节省约一半，证明该算法可以优化囊匣装箱。

5 结语

本文提出了新的层间垫平的三维囊匣装箱问题，根据使用衬垫体积最小的优化目标，设计了基于贪心策略与装箱顺序策略的混合启发式算法。将囊匣装箱问题分解为2步进行优化，分析了目标函数、装箱约束等因素，建立算法流程，编写程序求解出了合适的装箱方案与衬垫方案，并对输出效果进行了改进，解决了囊匣装箱问题。工作人员可以按照衬垫方案提前制作衬垫，根据装箱方案来摆放囊匣，保证了装箱工作的连续性与时效性。实例运行与对比验证证明，该算法计算出的装箱方案较人工装箱装载率更高，耗费衬垫减少，消耗时间短，更具经济性，有较好的运算能力与输出效果，可以使囊匣装箱智能化，推动了文物、艺术品领域的智能管理进程。

[1] 郭孙昊, 俞朝晖, 刘省珍, 等. 文物包装技术研究进展和智能化发展趋势[J]. 北京印刷学院学报, 2022, 30(6): 73-78.

GUO S H, YU C H, LIU S Z, et al. Research Progress and Intelligent Development Trend of Cultural Relic Packaging Technology[J]. Journal of Beijing Institute of Graphic Communication, 2022, 30(6): 73-78.

[2] DYCKHOFF H. A typology of Cutting and Packing Problems[J]. European Journal of Operational Research, 1990(44): 145-159．

[3] NGUYEN T H, NGUYEN X T. Space Splitting and Merging Technique for Online 3-D Bin Packing[J]. Mathematics, 2023, 11(8): 1912.

[4] CHEN M, HUO J, DUAN Y. A Hybrid Biogeography-Based Optimization Algorithm for Three- Dimensional Bin Size Designing and Packing Problem[J]. Computers & Industrial Engineering, 2023, 180: 109239.

[5] ROMERO S V, OSABA E, VILLAR-RODRIGUEZ E, et al. Hybrid Approach for Solving Real-World Bin Packing Problem Instances Using Quantum Annealers[J]. Scientific Reports, 2023, 13(1): 11777.

[6] 周丽, 杨江龙, 赵俊辉, 等. 基于混合遗传算法的多箱型三维装箱问题研究[J]. 包装工程, 2022, 43(21): 213-223.

ZHOU L, YANG J L, ZHAO J H, et al. Research on Multi Box 3D Packing Problem Based on Hybrid Genetic Algorithm[J]. Packaging Engineering, 2022, 43(21): 213-223.

[7] 王洁, 陶涛, 陈星艳, 等. 蚁群算法在定制家具矩形零件排样中的应用[J]. 林业工程学报, 2022, 7(1): 192-196.

WANG J, TAO T, CHEN X Y, et al. Research on Layout of Rectangular Parts of Customized Furniture Based on Ant Colony Algorithm[J]. Journal of Forestry Engineering, 2022, 7(1): 192-196.

[8] 陈仕军, 许继影. 改进邻域搜索算法的矩形件排样优化研究[J]. 山西师范大学学报(自然科学版), 2022, 36(1): 49-55.

CHEN S J, XU J Y. Optimal Rectangle Packing Based on Improved Neighborhood Search Algorithm[J]. Journal of Shanxi Normal University (Natural Science Edition), 2022, 36(1): 49-55.

[9] ÖZGE Ş, GÜNEŞ E. A Large Neighbourhood Search Algorithm for Solving Container Loading Problems[J]. Computers & Operations Research, 2023, 154: 106199.

[10] 阳名钢, 陈梦烦, 杨双远, 等. 求解二维装箱问题的强化学习启发式算法[J]. 软件学报, 2021, 32(12): 3684-3697.

YANG M G, CHEN M F, YANG S Y, et al. Reinforcement Learning Heuristic Algorithm for Solving the Two-Dimensional Strip Packing Problem[J]. Journal of Software, 2021, 32(12): 3684-3697.

[11] QUE Q Q, YANG F, ZHANG D F. Solving 3D Packing Problem Using Transformer Network and Reinforcement Learning[J]. Expert Systems with Applications, 2023, 214: 119153.

[12] 张德富, 彭煜, 朱文兴, 等. 求解三维装箱问题的混合模拟退火算法[J]. 计算机学报, 2009, 32(11): 2147-2156.

ZHANG D F, PENG Y, ZHU W X, et al. A Hybrid Simulated Annealing Algorithm for the Three-Dimensional Packing Problem[J]. Chinese Journal of Computers, 2009, 32(11): 2147-2156.

[13] 李瑞民. 文物藏品管理工作中存在的问题与对策研究[J]. 中国民族博览, 2019(3): 237-238.

LI R M. Research on the Problems and Countermeasures in the Management of Cultural Relics Collection[J]. China National Exhibition, 2019(3): 237-238.

[14] 张岚. 藏品囊匣制作的必要性[J]. 文物鉴定与鉴赏, 2021(22): 96-98.

ZHANG L. The Necessity of Making Collection Capsule Boxes[J]. Identification and Appreciation to Cultural Relics, 2021(22):96-98.

[15] 国家质量监督检验检疫总局, 中国国家标准化管理委员会. 文物运输包装规范: GB/T 23862—2009[S]. 北京: 中国标准出版社, 2009.

General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, Standardization Administration of the People’s Republic of China. Specification of Shipping Packaging of Cultural Relics: GB/T 23862-2009[S]. Beijing: Standards Press of China, 2009.

[16] 钱叶霞, 陈子敬. 基于改进模拟退火算法的配送路径优化研究[J]. 中国商论, 2023(8): 86-89.

QIAN Y X, CHEN Z J. Research on Distribution Route Optimization Based on Improved Simulated Annealing Algorithm[J]. China Journal of Commerce, 2023(8): 86-89.

Optimal Design of 3D Packing for Capsule Boxes Based on Interlayer Cushion

LI Guozhi1a,b, LI Yingxin1a,b, LUO Bobo2, LIU Di1a,b, TAN Sike1a,b, LI Wenfeng1c*

(1. a. Key Laboratory of Functional Printing and Transport Packaging of China National Light Industry, b. National Demonstration Center for Experimental Light Chemistry Engineering Education, c. School of Art and Design, Shaanxi University of Science & Technology, Xi'an 710021, China; 2.Emperor Qinshihuang's Mausoleum Site Museum, Xi'an 710600, China)

The work aims to study the strongly heterogeneous three-dimensional packing problem with interlayer cushion, realize the rapid calculation of the packing and the cushion scheme of the capsule box to instruct the packing, so as to improve the packing rate and efficiency of the capsule box, this work. Based on the actual packing requirements of the capsule box, a two-step optimization heuristic algorithm based on greedy strategy and improved packing sequence strategy was designed to optimize the packing and cushion scheme with the goal of minimizing the volume of the cushion. And according to different placement directions, different output results were designed to instruct packing. Compared with the data before packing optimization, the experimental results showed that the packing scheme and the cushion scheme recommended by this algorithm could reduce the number and volume of wooden cases, reduce the volume of cushion by 7.21%, and save about half the packing time. The hybrid heuristic algorithm designed in this paper can find the optimal packing and cushion scheme for the capsule box packing problem, reduce the use of cushion, and improve the packing rate and efficiency.

capsule box; three-dimensional packing; cushion generation; greedy strategy; heuristic algorithm

U294.29；TB485.3

A

1001-3563(2024)07-0159-07

10.19554/j.cnki.1001-3563.2024.07.020

2023-08-22

国家自然科学基金项目（51575327）；陕西省教育厅重点实验室及基地科研项目（16JS014）

通信作者