基于低相干干涉的孔类零件内表面测量系统研究

陈骏，丁斌，毛敏，陈宁，郭钢祥，祖洪飞

(1. 浙江理工大学机械工程学院，浙江杭州 310018；2.南通市计量检定测试所，江苏南通 226001；3.浙江省计量科学研究院，浙江杭州 310018)

0 前言

随着制造业的快速发展与进步，航空、汽车、船舶等领域对精密孔类零件的需求也越来越大，常见的孔类零件有油缸、轴承、阀套、轴套等[1]。上述应用通常要求这些孔类零件具有很高的加工精度和内表面质量，特别是涉及到轴孔配合的场合，如轴承和转轴的配合以及活塞杆和缸筒的配合等。然而，加工过程中刀具的磨损、系统的振动或零件的长期使用，都可能导致零件的实际尺寸与设计尺寸存在一定的偏差，这不仅会影响零件的使用寿命和工作性能，甚至还会使应用此零件的系统瘫痪，带来巨大损失。KALIDAS等[2]测量了干式钻孔过程中，热弹性效应对孔半径造成的误差，其测量得到的半径误差最大可达80 μm；GUPTA等[3-4]研究了刀具的对准误差对孔内表面加工的影响，从实验结果可知：轴的偏移和轴的倾斜都会导致孔出现最大可达100 μm的形状误差。因此，测量孔类零件内表面，有助于判断零件的加工质量和使用状态，是对孔类零件进行质量监测和故障诊断的有效手段。

目前，孔类零件内表面的测量方法主要有CCTV摄像法[5]、CT图像法[6]、光环截面法[7]等。CCTV摄像法主要通过爬行器带动CCTV摄像机在管道内部移动拍摄内壁图像，实现对内表面的测量，应用此方法的系统结构通常较为庞大复杂，无法测量小孔径的被测件；CT图像法利用X射线的物理特性对被测面进行无损检测，但此方法测量精度相对较低，无法满足高精度测量场合要求；光环截面法检测系统一般包括激光器、光学系统、摄像机以及计算机等，通过环形光对管件内壁进行测量，利用该方法进行测量时需要注意摄像机与激光器之间的相对位置，否则会引入较大的测量误差，影响测量精度。基于干涉原理的检测方法，由于其较高的测量精度，因此被广泛应用于工业测量领域；其中，低相干干涉检测法利用宽带光源的干涉特性[8]，成为另一种区别于激光干涉检测法的高精度测量方法。

1 低相干干涉测量原理

由双光束干涉理论[15-16]可知，两束特定波长的单色光发生强相干干涉时，迈克尔逊干涉仪产生的干涉光强值可表示[17]为

(1)

其中：Δ=nl为两路光的光程差；A0为干涉直流分量；A1为干涉信号的可见度；δ为两路光的相位差；λ为光源波长。基于式(1)，强相干干涉光强与光程差关系如图1(a)所示，可知：强相干干涉光强的幅值不会随着光程差的变化而发生改变，始终保持稳定。

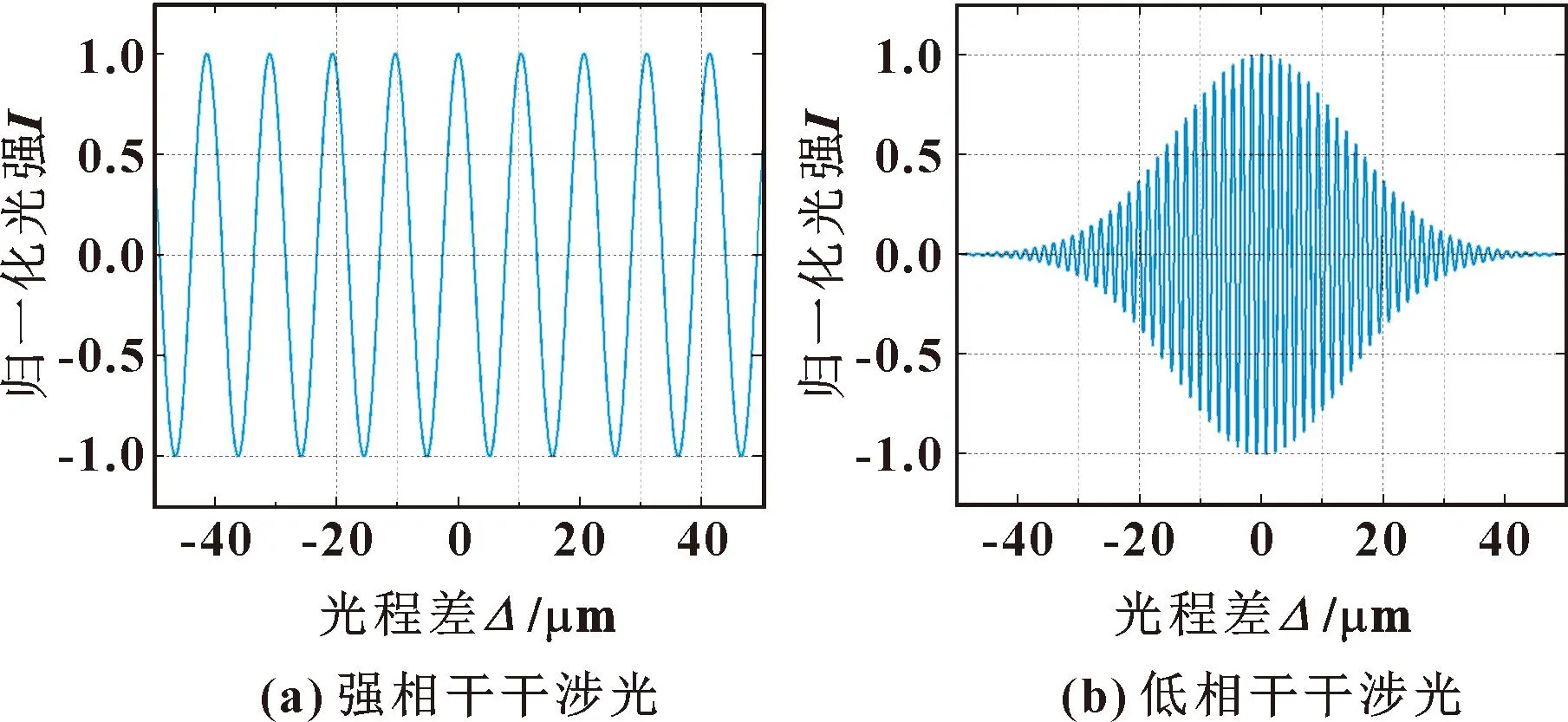
图1 不同光源光强与光程差关系

然而，对于低相干干涉而言，由于宽带光源的特性，其干涉光强可视为由不同波长的单色光分别干涉并叠加而成。此时式(1)中，λ为宽带光源的所有波长，干涉强度表达式则变为以λ的变化范围为积分上下限的积分式，如下式所示：

(2)

其中：λ0为光源中心波长；λm为光源光谱半宽；φ(λ)为干涉信号关于λ的能量分布。基于式(2)可得到低相干干涉光强与光程差关系如图1(b)所示。可知：光程差为零处对应等光程点，此时干涉光强出现极大值，并且随着光程差的增加而快速减小，因此低相干干涉系统通过将等光程点作为系统位置标记可以实现非常高精度的定位及测量。

2 孔类零件内表面测量系统结构

如图2所示，本文作者设计及搭建的孔类零件内表面测量系统主要由宽带光源(索雷博Thorlabs，SLD850S)、3dB耦合器、光电探测器、数据采集仪(亿恒ECON，MI-7008)、参考臂和样品臂组成。宽带光源中心波长λ0为850 nm，半谱宽度Δλ为60 nm，光谱形状为高斯型，则其相干长度lc可由如下公式计算而得：

(3)

图2 内表面测量系统结构示意

式中：ξ为光谱系数，其取值与光谱形状密切相关，当光谱为高斯型时，ξ取值为0.66。因此，可得此系统的相干长度约为8 μm。耦合器为2×2结构，分光比为50∶50，用于将宽带光源发出的光分为两路，分别射向参考臂和样品臂，然后接收两路反射光并产生干涉。光电探测器为硅基探测器，探测范围为350～1 100 nm，用于采集低相干干涉信号，并将干涉光信号转换为电信号进行传输。数据采集仪为多通道高速数据采集设备，可同时采集及处理数字信号与模拟信号，用于同时采集参考臂和样品臂位移台以及光电探测器的信号，并传输给上位机。参考臂由位移台、准直镜和安装在位移台上的平面反射镜组成，准直镜将参考光准直后照射到平面反射镜上并反射回耦合器进行干涉；位移台带动平面反射镜对被测件上测量点的等光程位置进行定位。样品臂通过探头实现对被测件内表面测量，其中探头由准直镜、离轴反射镜等部分组成，可实现光的准直、折射及聚焦。测量时，通过上位机控制探头及被测件的运动实现对内表面的连续测量，最终通过相应的信号处理算法对内部特征进行表征。

3 干涉信号处理

理论上，宽带光源的低相干干涉信号是关于零光程差位置左右对称的，然而由于散粒噪声、相对强度噪声、热噪声等的干扰，实际得到的干涉信号的信噪比较低，不利于对零光程差位置的定位和提取，因此，需要对干涉信号进行滤波预处理。光正入射运动物体的多普勒频率与波长、速度之间的关系为

韩语是韩国文化的一部分，韩国文化的传播与交流离不开韩语。韩语是韩国文化传播、交流以及发展的主要媒介，人们往往通过学习韩语来对韩国文化进行掌握与了解，从而认识韩国这个国家。

(4)

式中：f0表示信号频率；v表示位移台的运行速度；λ0表示宽带光源的中心波长，为850 nm。根据位移台运行速度设定值10 mm/s，可以计算得到f0为23.5 kHz。因此，根据所得f0选择带通滤波器的频率为22.5～24.5 kHz，中心频率为23.5 kHz。

滤波处理可以有效提高原始信号的信噪比，下一步需要利用对零光程差点位置进行准确提取。由于干涉图样中心条纹的峰值对应零光程差点，因此对低相干干涉信号中心条纹或信号包络极值的识别算法尤为重要。常见的包络解调方法包括包络曲线拟合法、傅里叶变换法、希尔伯特变换法和小波变换法等。其中，小波变换法是近年来发展起来的一种针对信号时频特性的分析方法[18]，被广泛应用于图像处理、电子对抗和计算机识别等领域。小波变换法克服了傅里叶变换法的时频局限性，它能够对目标信号进行有选择的时频局部化观察。小波变换的局部极大值可为分析信号奇异性提供足够的信息，并可在不同分辨率下对信号分层分析以及在不同频段内对噪声进行滤波，因此在较强的噪声下，小波变换法的包络提取精度优于傅里叶变换法、希尔伯特变换法等。因此此系统使用小波变换法对干涉信号进行处理，提取零光程差点。

设Ψ(t)为母小波，则小波族定义为

(5)

式中：a为尺度伸缩参数，通过改变a值使子小波的中心频率和带宽发生变化；b为平移参数，改变b将使子小波的位置发生平移，从而可对目标函数感兴趣的区域进行提取。对于任意平方可积函数X(t)，小波变换可以定义为

(6)

式中：Ψ*(t)表示Ψ(t)的共轭函数。

由法国地球物理学家MORLET等[19]提出的Morlet小波是一个具有高斯包络的复调制信号，因其在形式上与低相干干涉信号极为类似，因此众多研究者选择Morlet小波对干涉信号进行分析。以Morlet小波为母小波，对干涉信号进行小波变换可以得到

Wm(a,b)=Wmr(a,b)+jWmi(a,b)

(7)

则干涉信号的包络表示如下：

(8)

式中：|Wm(a,b)|为小波系数；Wmr(a,b)和Wmi(a,b)分别为干涉信号进行Morlet小波变换后的实部和虚部。通过改变b的大小使子小波在目标函数上不断滑动，当小波函数与所分析的干涉信号重叠度最高时，小波系数取得最大值，此时即可通过确定小波包络峰值来定位干涉信号的零光程差点位置。利用小波变换法对不同测量点的零光程差点进行定位并用三维点云表示，最终便能实现对内表面的测量。

4 实验与分析

4.1 系统测量稳定性实验

较高的测量稳定性是保证测量结果可靠的前提，因此在对内表面进行测量之前，需对系统测量稳定性进行验证。以平面反射镜为被测件，对其反射面上某一点重复测量1 000次，利用Morlet小波变换对每一次测量得到的干涉信号进行处理得到测量结果xi，最终，通过1 000次测量结果的标准差σ表征此系统的测量稳定性。图3为该被测点某次测量得到的干涉信号以及Morlet小波包络，图4为对被测点测量1 000次得到的零光程差位置。

图3 被测点的干涉信号及Morlet小波包络

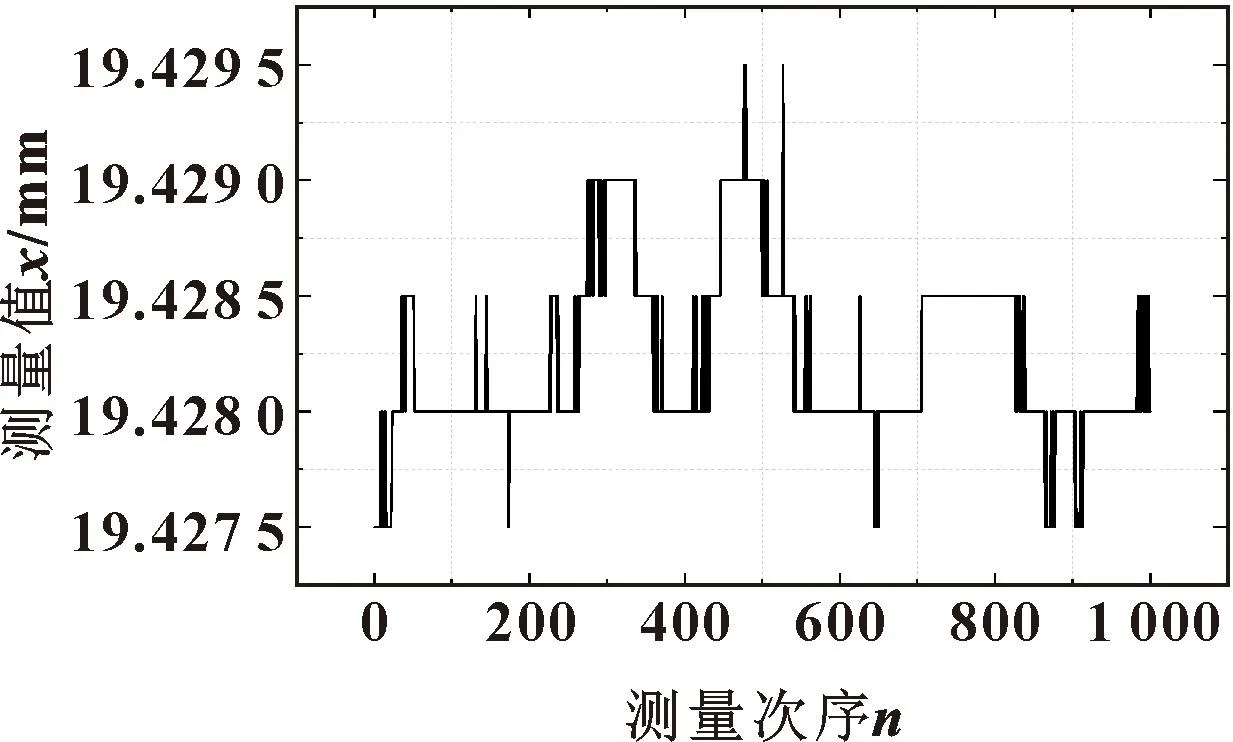
图4 被测点1 000次测量结果

标准差σ通过如下所示贝塞尔公式计算得出：

(9)

4.2 系统标定实验

由测量原理可知，若要获得准确的测量结果，需要将测量得到的相对距离转化为实际距离，即对系统进行标定。选取1个内径计量值D0为50.002 3 mm的标准环规，在其中截面位置对100个等间隔采样点测量一周，不同采样点的等光程差位置如图5所示。为了尽可能消除随机误差对标定结果的影响，以100个采样点等光程差位置的平均值作为标定结果，计算出参考位置P0，此处P0=19.503 8 mm。系统标定后，可进行其他被测件的测量。将被测件的等光程差位置记为Pi，其相对标定环规移动距离记为li，则该被测件的内径Di可由式(10)计算得出：

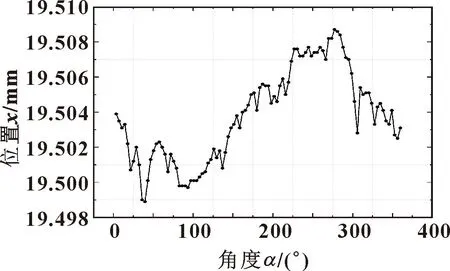
图5 系统标定

Di=D0+2(P0-Pi+li)

(10)

4.3 环规内径测量实验

为了验证此系统的测量精度，使用标定后的系统对计量直径为70.002 4 mm的环规内径进行测量，测量结果如表1所示。可知：70 mm环规的测量结果平均值为69.995 8 mm，与计量值相差6.6 μm，6次测量结果的标准差为0.6 μm，表明此系统具有较高的测量精度和测量重复性。

表1 70 mm环规测量结果

4.4 扩口管锥度测量实验

扩口管广泛应用于工业领域的高压管路中，诸如船舶、金属加工和采矿等，其锥度大小对管路的密封性、气体或液体的流速都会产生影响，因此对扩口管锥度的测量有重要意义。利用此系统对如图6所示的扩口管进行测量，并调用PolyWorks软件将得到的三维点云进行特征拟合，形成圆台面，如图7所示。对于圆台而言，锥度T的计算公式如下：

(11)

图6 扩口管实物(a)及剖面图(b)

图7 扩口管三维点云

式中：D和d分别为圆台上、下底面的直径；H为圆台高度。实验所用扩口管上底面直径为30 mm，下底面为14.5 mm，高度为50 mm，锥度T为0.31。

从图7所示点云中选取2个截面，如图8所示，通过软件得到的各个截面直径以及式(11)，计算出该扩口管锥度为0.311 7≈0.31。此结果与设计值基本一致，体现系统对变径被测件的测量能力。

图8 锥度计算点云

4.5 内螺纹测量实验

内螺纹在各行各业均使用十分广泛，不同场合对螺纹的要求也不尽相同，比如光学精密仪器上通常采用细牙螺纹；T型螺纹由于其强度高、对中性好，在传动领域使用十分频繁。螺纹的螺距是设计及加工时需要考虑的重要参数，螺距越大，牙的强度也就越高，但螺距越大，同样直径的螺栓心部也就越细，螺栓心部强度就越低，因此，工程上对螺距测量有重要需求。利用此系统对图9所示内螺纹进行测量，测量结果经三维建模后如图10所示。可知：螺距的测量值为3.173 mm，与此被测件的实际螺距3.175 mm仅相差2 μm。证明此系统具备对内螺纹进行测量的能力，且测量精度很高。

图9 内螺纹被测件

图10 内螺纹三维点云

5 结论

文中针对精工行业对高精密孔类零件内表面尺寸和相关特征的测试需求，基于低相干干涉原理，设计并搭建了可用于孔类零件内表面测量的系统。并进一步通过环规、扩口管、内螺纹等实物测试验证了该系统具备对孔类零件内表面进行高精度测量及特征参数表征的能力。