基于梁结构等效模型的机器人铣削有限元仿真

曾峥嵘，周勇，胡楷雄，李卫东

(1.武汉理工大学交通与物流工程学院，湖北武汉 430063；2.上海理工大学机械工程学院，上海 200093)

0 前言

铣削加工的工艺参数影响着零件加工精度与表面质量的好坏。随着有限元软件的发展，有限元仿真在切削加工工艺参数优化中得到了广泛的应用。例如，利用AdvantEdge软件建立有限元模型分析刀具几何参数对铣削力的影响[1]；采用Deform-3D软件模拟不同几何参数刀具的铣削加工来优化刀具结构[2-3]；基于Abaqus软件建立皮质骨加工模型，寻找最优的切削参数[4-5]；利用Abaqus仿真寻找最佳刀轴倾角[6]。上述研究主要针对机床加工的工艺参数优化进行仿真，通常忽略了设备刚度对切削的影响。

相较于机床，工业机器人用于铣削加工具有工作范围广、灵活性高等优点。然而机器人的弱刚度特性会导致铣削加工过程中较大的末端变形，影响加工质量[7]。因此，众多研究者提出了多种刚度性能指标用于优化机器人姿态。CHEN等[8]提出了用于优化机器人姿态的曲面法向柔度系数指标。段现银等[9]采用曲面法向柔度系数指标，有效提高了零件曲面法向轮廓精度。PENG等[10]使用柔度椭球体积评价机器人末端整体变形量。GUO等[11]提出了基于切削力的刚度指标，更全面地评价机器人姿态。ZHU等[12]利用基于切削力的刚度指标结合材料去除率优化刀轴倾角，但该指标计算比较复杂耗时。通过机器人铣削仿真可以提前预测机器人运行情况，并在缺乏实际铣削实验与专用测量仪器的情况下为机器人铣削加工的姿态优化提供理论基础。如MOUSAVI等[13]建立了工业机器人的有限元数值模型，分析了冗余角对加工颤振的影响；但该模型主要针对机器人整体结构进行构建，尺寸大且建立繁琐，如更换机器人型号则需要重新建模。

本文作者针对机器人铣削加工过程的末端变形情况，采用Abaqus软件建立机器人铣削加工有限元模型，根据机器人末端刚度与铣削加工的振动特点将机器人末端变形等效为梁的拉压变形，模型通用性好且易于模拟机器人不同姿态下的末端变形情况。最后设计力锤实验获取梁结构动力学参数，通过铣削实验对模型的正确性进行验证，并基于仿真对两种不同的机器人刚度性能指标进行对比分析。

1 铣刀-工件有限元仿真模型

表1 球头铣刀参数

在Abaqus软件中采用修正后的Johnson-Cook (J-C) 本构模型与物理分离准则的J-C失效模型定义6061铝合金的材料属性，表2、3为模型所采用的属性参数[14-15]。

表2 J-C本构模型

表3 材料失效参数

综合考虑仿真计算量与精度，预先对模型进行多种网格尺寸的短时仿真对比，发现网格尺寸为0.3 mm时较为合适。定义刀具为刚体约束，不考虑磨损情况，刀具与工件网格节点法向行为为硬接触，切向摩擦因数为0.7。

2 梁结构等效的机器人铣削有限元模型

在刀具-工件有限元模型基础上分析机器人末端特性，添加梁结构建立机器人铣削有限元模型。

2.1 机器人柔度矩阵

针对KUKA KR60-3机器人铣削加工进行研究，首先采用改进D-H法建立机器人运动学模型，再基于运动学模型获取机器人柔度矩阵。利用MATLAB计算运动学对应的雅可比矩阵，通过关节刚度与雅可比矩阵计算末端刚度矩阵。为了便于后续变形计算，采用公式(1)直接求解末端刚度矩阵的逆矩阵，即柔度矩阵：

(1)

其中：Jθ为机器人雅可比矩阵；Kθ为关节刚度矩阵；Cfd为力-平移柔度矩阵；Cfδ为力-旋转柔度矩阵；Cmd为扭矩-平移柔度矩阵；Cmδ为扭矩-旋转柔度矩阵。通常情况只考虑由机器人末端受力引起的平移变形，后续针对力-位移柔度矩阵计算末端变形量。

2.2 机器人末端振动分析

实际铣削加工过程中，机器人末端在动态铣削力作用下产生受迫振动。将机器人末端简化为多自由度线性系统，可看作单自由度系统的线性叠加，考虑机器人末端的平移变形，可将机器人末端振动分解为X、Y、Z三方向的单自由振动系统。

将机器人末端主轴部分在基坐标系的三轴方向振动均简化为如图1所示的动力学模型，由公式(2)所示的微分方程表述：

下面介绍一个持续长度的概念,它是蠕虫状链模型中的重要参数.对于一条由键长为l、键角为α的n个键所组成的大分子链,将第一个键的方向看成z轴(见图1),那么第二个键以α角与之相连,键矢量间的夹角为θ,第三个键又以α角与第二个键相连,其键矢量间的夹角亦为θ,依次类推,这条链的末端距在z轴上投影的平均长度即为n个键矢量在z轴投影长度的加和:

(2)

图1 单自由度系统动力学模型

其中：ma为等效质量；Ca为等效阻尼；Ka为等效刚度，通过柔度矩阵获取；F(t)为随时间变化的铣削力；X(t)为振动位移，振动位移包含与切削力频率相同的受迫振动部分和初始条件引起的自由振动部分。

2.3 梁结构等效机器人末端的有限元模型

基于上述机器人末端振动变形分析，采用悬臂梁结构等效单自由度振动系统的动力学模型。根据材料力学知识，悬臂梁的拉伸变形可根据公式(3)进行计算：

(3)

其中：F为作用于梁端部垂直截面的外力；L0为悬臂梁原始长度；L1为悬臂梁拉伸变形后长度；E为梁材料弹性模量；A为梁截面面积，常用的梁截面中矩形截面计算较为简单，适合作为等效梁截面。

机器人末端平移变形如公式(4)所示：

(4)

其中：[xyz]T为机器人末端平移变形列向量；[FxFyFz]T为机器人末端外力列向量。

根据公式(4)可知，机器人末端在某方向产生的位移由三方向的外力共同决定，并与机器人柔度相关。故为获取末端在刀位点坐标系的某一轴向变形，需得到三方向外力作用下的变形量并进行叠加。

将机器人在刀位点坐标系三轴方向的变形等效为3根悬臂梁的拉压变形，通过公式(5)计算得到三方向上的刚度大小分别为k1、k2、k3。公式中3根梁的横截面积A与长度L0大小一致且始终设置为固定值；Cij根据公式(4)选取，i取决于仿真模拟的变形方向，j取决于外力方向。文中首先模拟Z轴方向变形，故先选取C31、C32、C33进行计算。

(5)

当给定某一机器人姿态时，通过柔度矩阵计算公式(1)将所需的柔度元素值代入公式(5)，获取梁结构弹性模量参数E。为梁结构赋予等效质量与阻尼后即可模拟给定姿态机器人铣削加工中末端的Z向变形情况。

在Abaqus中建立给定几何尺寸的矩形截面梁，并赋予材料属性。创建连接梁端点与刀具中心点的线条，线条连接特征为铰连接，即只允许刀具相对于梁端点进行自身旋转。分别为刀具添加旋转速度、为工件底部节点添加进给速度，并约束梁整体只发生轴向变形。图2所示为所建立的机器人铣削加工有限元模型，通过该模型可模拟指定机器人姿态下刀位点坐标系任一轴向上的机器人末端变形情况。

图2 基于梁结构等效机器人末端的有限元模型

3 仿真模型实验验证与应用

3.1 机器人末端力锤实验

通过力锤敲击实验测量机器人末端固有频率，间接获取等效质量与阻尼，完善模型参数。锤击实验采用三向加速度传感器，设置数据采集频率为6 000 Hz，获取6个姿态下的机器人末端固有频率。表4所示为6组姿态的锤击实验测量结果，发现不同敲击力与不同姿态下的机器人末端三方向的固有频率在较小区间变化，可采用固有频率平均值作为参数。图3为Z向固有频率示意。

图3 测量的末端Z向固有频率

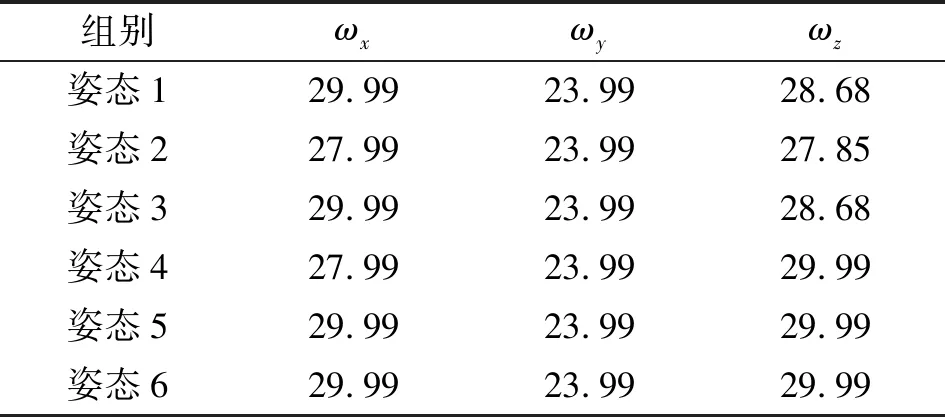
表4 机器人部分姿态末端固有频率 单位：Hz

瑞利比例阻尼模型符合机器人运动情况，如公式(6)所示[16]，用于梁结构参数设置，设置阻尼系数分别为αM=0.672 1和αK=0.148 6。

Ca=αMMa+αKKa

(6)

3.2 机器人铣削轮廓误差与铣削力实验

为了验证模型准确性，采用KUKA KR60-3机器人进行6061铝合金的球头铣刀铣削实验，利用Keyence LJ-V7080型超高速线激光轮廓扫描仪采集铣削实验的表面轮廓信息，采用Kistler 9129AA测力仪和Kistler 5070电荷放大器测量铣削力。实验装置如图4所示。

图4 机器人铣削实验平台

通过激光扫描仪获取轮廓曲线，扫描频率为200 Hz，扫描速度为1 mm/s。为避免偶然性，进行3次重复实验，对测量值取平均值。表5为实验与仿真结果数据。

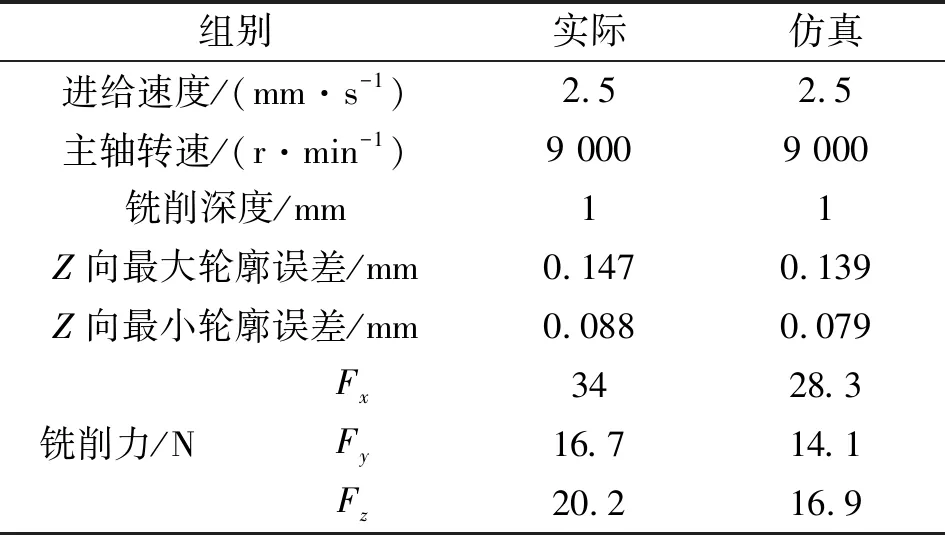
表5 实验与仿真测量结果对比

表5中仿真与实验的铣削力存在误差的原因在于仿真模型设置的加工条件较为理想化，仿真过程不考虑机器人自身定位误差、刀具变形磨损、水冷降温、工件不平整等因素，因此模拟的铣削过程更加平稳，数值更小。图5为实际铣削加工与仿真的轮廓误差曲线，可知仿真与实际最大轮廓误差的相对误差为5.4%，最小轮廓误差的相对误差为10.2%，基本符合实际铣削情况。表明基于梁结构等效机器人末端的有限元模型可以有效地仿真机器人铣削加工中的末端变形情况。

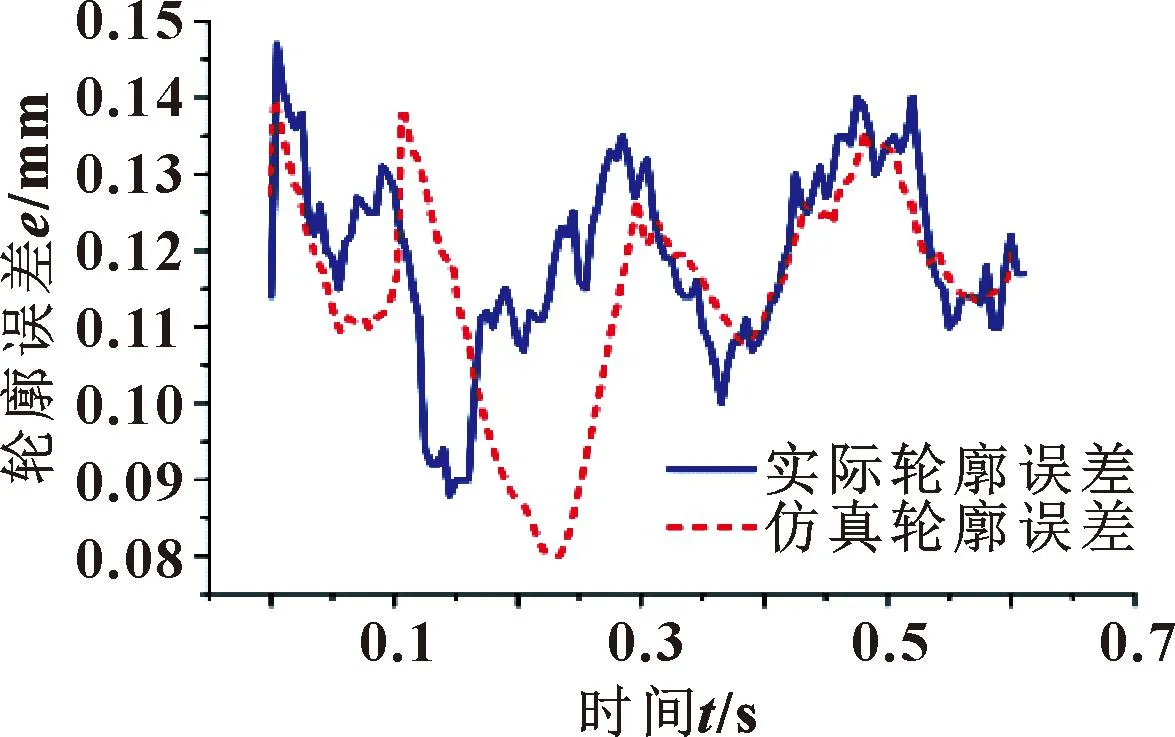
图5 实际与仿真轮廓误差曲线对比

3.3 机器人刚度指标仿真对比分析

本文作者针对常用的两种刚度性能指标进行仿真对比，分别是基于工件几何形状的曲面法向柔度系数指标cn[8]和考虑切削力的刚度指标cf[11]。指标定义如公式(7)所示：

(7)

其中：en为曲面法向方向的单位矢量；ef为切削力方向的单位矢量。指标cn用于评价机器人末端在工件表面法向受单位切削力时的变形程度，指标cf评价机器人末端受单位切削力时，在切削力方向的变形程度，因此指标cf需要提前知道铣削力方向。

通过指标公式可知，指标cf评价了机器人末端在切削力方向上的整体变形程度，指标cn只考虑了机器人末端在工件表面法向的抗变形能力，因此指标cf较指标cn考虑更全面，但指标cf需要提前计算铣削力方向，更加耗时。为进一步分析，进行仿真实验对比。选取相同末端位置的9组不同冗余角对应的姿态进行刚度指标计算，冗余角取值范围为±40°，取值间隔为10°，表6为部分姿态对应的刚度指标。根据指标差异选取冗余角为-40°与40°的两组姿态进行仿真实验，设置刀具进给速度为2.5 mm/s，旋转速度为9 000 r/min，切削深度为1 mm。

表6 相同末端位置下不同冗余角的刚度指标

仿真对比结果如表7所示，姿态2的总变形量略小于姿态1，但Z向(法向)变形量明显大于姿态1。在曲面铣削加工过程中，法向轮廓误差是影响曲面加工精度的主要因素[8-9]，可得出结论：虽然通过指标cf优化机器人姿态可保证总变形量较优，但优势不明显，而指标cn可以更好地优化法向加工精度，更适用于曲面加工。同时指标cn计算更简便，在效率上优于指标cf。在不需要进行加工精度极为苛刻的铣削任务时，推荐使用曲面法向柔度系数指标。

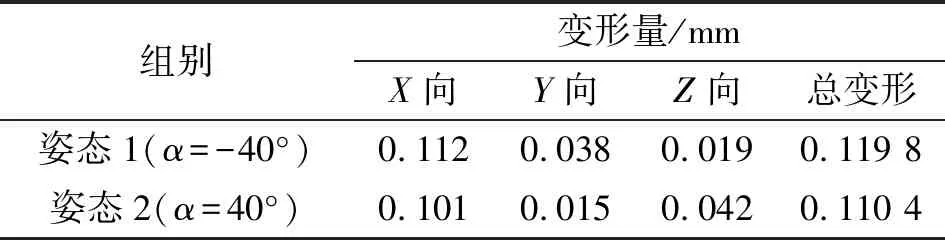
表7 刚度性能指标仿真对比

4 结论

利用梁结构建立了考虑机器人弱刚度特性的铣削有限元模型，通过6061铝合金的球头铣刀铣削实验验证了仿真模型的正确性，最后对比实验指导刚度性能指标的选取，得到以下结论：

(1)考虑机器人的弱刚度特性，将机器人末端变形与姿态相联系，在刀具-工件有限元模型中添加与机器人姿态相关的梁结构来等效机器人末端变形情况，实验结果表明：基于梁结构等效模型建立的铣削有限元模型可以正确模拟机器人铣削加工过程。

(2)通过在所提出模型上的仿真对比发现，基于考虑切削力的刚度指标cf优化机器人姿态可以保证机器人末端总变形量最小，但无法约束特定方向的变形情况。基于工件的指标cn对提升法向加工精度有显著的效果，从效率和加工需求判断，指标cn比指标cf更适用于优化机器人铣削加工曲面的姿态。