基于改进多目标平衡优化器算法的点焊机器人路径规划

赵云涛，甘镭，李维刚

(武汉科技大学，冶金自动化与检测技术教育部工程研究中心，湖北武汉 430081)

0 前言

机器人在车身焊接中应用广泛，但传统点焊的路径规划多采用手工教学方法。手工教学方法的焊接质量取决于工人的技能和经验，焊接质量不能保证。因此，需要采用自动、有效的路径优化方法。规划合理的焊接路径、提高生产效率是当前研究的热点。

点焊机器人的路径规划是一个最优化问题。根据给定的焊点，规划机器人焊枪通过这些符合相应约束条件的焊点运动的最佳路径。王学武等[1]针对弧焊机器人的路径长度和能耗比提出了一种自适应邻域的离散DMOEA/D-ET算法，通过触发机制选择全局搜索和局部勘探两种策略，局部搜索采用MOEA/D算法。高明、陆颖[2]针对汽车引擎盖焊接的路径规划问题，提出一种改进蚁群算法，对原始蚁群算法的信息素更新加入自适应混沌策略，局部信息素根据蚁群密度自适应变化，全局信息素则结合混沌扰动进行更新，信息素的改进提高了多样性和随机性。文献[3]指出对于焊接机器人的规划，路径长度和周期时间非常重要，针对焊接机器人建立了路径和时间模型，并提出一种采用聚类引导的多目标粒子群算法来解决点焊机器人的路径规划问题。

平衡优化器算法(Equilibrium Optimizer，EO)是FARAMARZI等[4]受控制容积质量平衡的物理现象启发于2020年提出的一种新型优化算法。和传统的启发式算法相比，平衡优化器算法具有寻优能力强、精度高等特点；但EO算法也存在着易陷入局部最优、收敛精度低等问题。针对这些问题，已有许多学者对平衡优化算法进行了改进。例如：TANG等[5]结合多种群策略并采用高斯分布估计策略和莱维飞行策略进行更新，提高了种群的多样性。MOUSA等[6]在平衡优化算法中加入混沌搜索策略，增强了算法的局部搜索能力。周鹏等人[7]融合了Tent混沌映射改进初始化种群，并且在迭代过程中加入透镜成像策略得到反向解进行更新，提高了算法跳出局部最优的能力。以上改进的平衡优化算法取得了较好的效果，但都是基于单目标问题的改进优化。在多目标优化问题中，PREMKUMAR等[8]将非支配排序和平衡优化器算法进行结合并且加入了存档集机制。目前没有平衡优化算法应用于处理离散问题的研究。

以高效解决点焊机器人的路径规划问题为目标，本文作者提出一种融合改进快速非支配排序的离散多目标平衡优化器算法(Discrete Multi-Objective Non-dominated Equilibrium Optimizer，DMONEO)。结合快速非支配排序策略，针对拥挤度因子不能很好地反映同层次解的密度，通过生存评分来替换拥挤度因子，可以更好地保持种群的多样性。最后通过精英策略，将当前种群和子代种群合并竞争从而使得表现较好的个体保留。

1 点焊机器人路径规划问题

机器人的路径规划可以简化为旅行商问题(Traveling Salesman Problem，TSP)。以一个焊接工件作为路径规划的对象，工件中有多个焊点。焊枪的运动代表了旅行销售员的行走。路径规划是为了寻找穿越所有焊点的最短路径。在实际生产作业中，达到最高效率是优化目的。因此，本文作者针对焊接时间和焊接路径建立了模型。

1.1 焊接时间模型

在焊接过程中，当机器人在焊接点{γ1，γ2，…，γi，…，γn}之间移动时，它对应于一个时间序列{t1，t2，…，ti，…，tn-1，tn}。ti表示焊点γi与焊点γi+1之间移动所需要的时间。tn为焊接时间，包括工作时间和移动时间。因为焊接所用的工作时间是固定的。为了简化问题，焊接时间主要考虑了焊点之间的移动时间。焊接时间的定义见式(1)

(1)

1.2 焊接长度模型

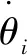
(2)

其中：σ5、σ4、σ3、σ2、σ1、σ0为系数；ti为时间。

焊点之间的运动轨迹γiγi+1在关节空间中可以分为等量的p段。根据等式计算轨迹上p个点的角位移θi1、…、θip，通过机器人的运动学分析，得到了p个点对应的笛卡尔坐标值。随着段数的增加，p段轨迹的和近似为路径长度qi，i+1

(3)

dj，j+1是p段轨迹中相邻点(aj,bj,cj)和(aj+1,bj+1,cj+1)之间的欧氏距离，定义见式(4)

(4)

移动路径的总长度计算见式(5)

(5)

1.3 多目标路径规划模型

将所建立的焊接路径长度模型和焊接时间模型作为路径规划的目标函数，以最大角速度和最大角加速度为约束条件，由此建立点焊机器人路径规划的多目标模型，见式(6)(7)

Minimize：f1(x)=L(x)

(6)

Minimize：f2(x)=T(x)

(7)

其中：x∈{x1,x2,…,xi,…,xΔ}是所有焊点顺序的集合。

2 平衡优化器算法

平衡优化器算法的思想参考了质量平衡模型[4]，见式(8)

(8)

其中：V代表控制容积；C表示控制容积内的浓度；Q为流进或流出控制容积的容量流速；Ceq表示控制容积内部在平衡时的浓度；G代表控制容积内部的质量生成速率。平衡优化器算法的流程如下：

(1)种群初始化

初始种群是根据种群规模在每个决策变量的上下界范围内进行随机初始化，见式(9)

(9)

其中：Cub、Clb分别为决策变量的上限和下限；ri为[0，1]之间的随机数向量，其维度跟空间维度一致。

(2)生成平衡状态池

更新过程中的候选解选自平衡状态池，见式(10)

Ceq,pool={Ceq,1,Ceq,2,Ceq,3,Ceq,4,Ceq,ave}

(10)

其中：Ceq，1、Ceq，2、Ceq，3、Ceq，4分别为当前种群中最好的4个解；Ceq，ave代表这4个解的平衡状态。更新过程中在平衡状态池里随机选取最优解。前4个候选解用于争取更好的勘探效果，第5个候选解为平衡值可以提高开发水平。

(3)指数项系数

指数项系数记为F，影响更新规则，定义见式(11)—(13)

F=exp[-λ(t-t0)]

(11)

(12)

t=(1-n/nmax)(a2n/nmax)

(13)

其中：a1、a2分别为全局勘探和局部开发的权重系数，一般分别取2和1；λ为[0，1]之间的随机数；n和nmax分别为目前迭代次数和终止迭代条件。

(4)生成率

生成率记为G，设计如下，见式(14)(16)

G=G0e-λ(t-t0)

(14)

G0=GCP(Ceq-λC)

(15)

(16)

其中：GCP为生成率控制参数，用于对迭代过程中的生成率进行控制；r1、r2和λ为[0，1]随机数向量，其维度跟优化空间维度一致；G0为生成率的初始值；GP为生成概率，一般取0.5。

(5)更新公式

C=Ceq+(C0-Ceq)F+G(1-F)/λV

(17)

平衡优化器算法主要基于式(17)展开迭代寻优。等式左边的浓度C代表新产生的解，C0代表上一次迭代得到的解，Ceq为从平衡状态池中随机选取的解，V一般取1。

3 离散化多目标平衡优化器算法

3.1 离散编码方式

TSP问题的解通常用路径编码来描述，即最终经过所有城市的排序。针对路径编码的信息更新，参考遗传的思想，即染色体的交叉变异进行信息的互换。交叉算子是产生新个体的主要方法，通过交换两个父代之间的部分信息得到两个新的子代。变异算子是对个体的某些序列上的信息进行改变，这种操作不需要进行信息交换。

在TSP问题中，邻域信息具有十分重要的作用。为了较好地保留领域信息以及更好地进行迭代更新，本文作者采用了顺序交叉算子和随机插入算子。

顺序交叉算子的操作见图1，可以分为以下3个步骤：

图1 交叉算子流程

(1)随机选择两个个体P1、P2作为父代以及两个随机点作为互换信息的起始点和终点。

(2)将P1、P2中两点之间信息提取出来，放在子代O1、O2的相同位置。

(3)将另一个父代按序删除已有的基因后将该序列填入O1。同理对O2进行操作。

随机插入算子的操作见图2，可以分为以下3个步骤：

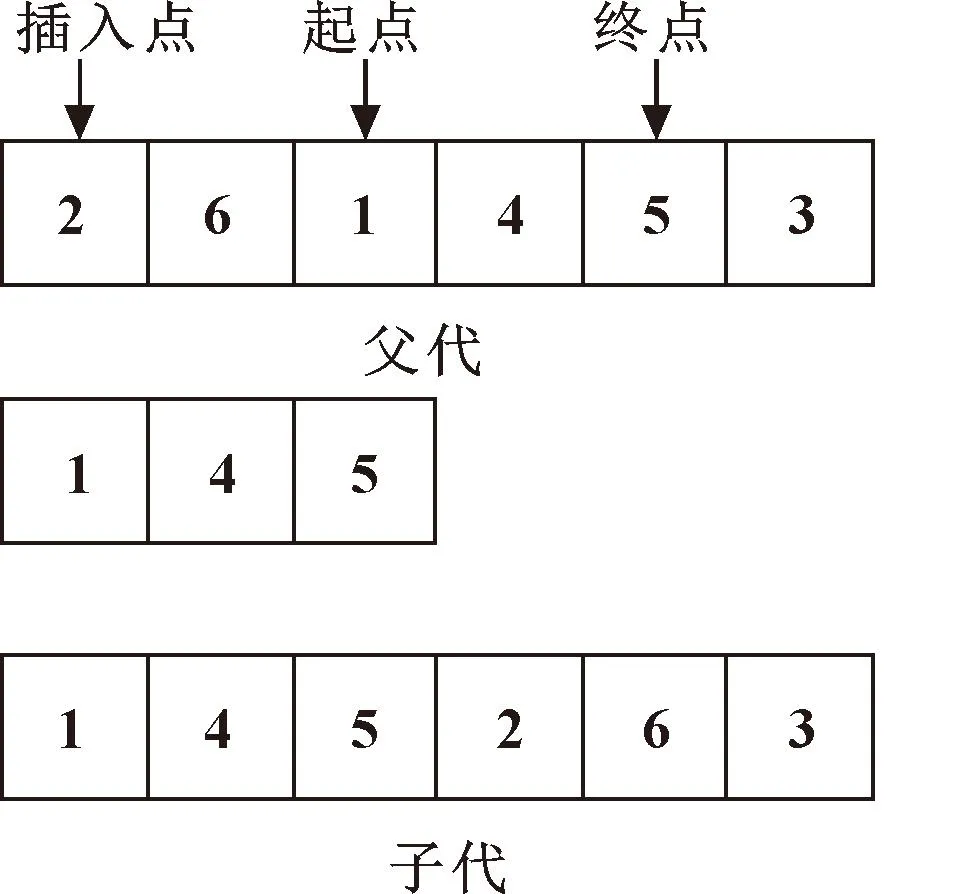
图2 变异算子流程

(1)父代随机选择3个点，分别作为插入点、保留领域信息的起点和终点。

(2)将起点和终点之间信息提取出来，从子代插入点的位置插入。

(3)将父代按序删除已有的基因后将该序列填入子代。

3.2 生存评分策略

文献[8]所提出的算法结合了非支配排序的策略。但文献[9]中提出的NSGA-II算法中通过拥堵因子并不能客观反映同层次中个体之间的真实拥挤程度。当两个或多个解具有同样的适应度时，计算出的拥挤距离值可能为0或者由个体在帕累托前序列中的位置所决定。针对这个缺点，本文作者采用了一种快速估计非支配前沿几何形状的策略[10]，使用一个结合非支配前沿多样性和邻近性的生存分数取代了拥挤距离。

生存评分计算步骤如下：

(1)归一化

在迭代过程中，使用非支配排序将种群划分为不同层次的非支配前沿。然后，对第一个非支配前沿进行标准化和归一化处理，见式(18)

(18)

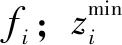
(2)计算Lp范数估计前沿集合形状

Lp范数用于计算接近度和多样性的距离。指数p是依据每代中第一个非支配前沿的几何形状所计算的，通过式(19)求指数p的值。

(19)

(20)

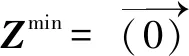
(3)计算生存评分

通过第一个非主导前沿F1的Lp范数，测量f1的多样性和邻近性。计算见式(21)(22)

(21)

(22)

一般解S∈F1的接近度得分为其目标向量fn(S)到理想点的距离，多样性得分为与前沿F1中其他解的最小距离。生存评分结合了多样性和邻近性，见式(23)

(23)

非支配前沿Fd>1中的解的生存得分为它们的近度得分的倒数。

3.3 算法流程

DMONEO算法的流程如图3所示。

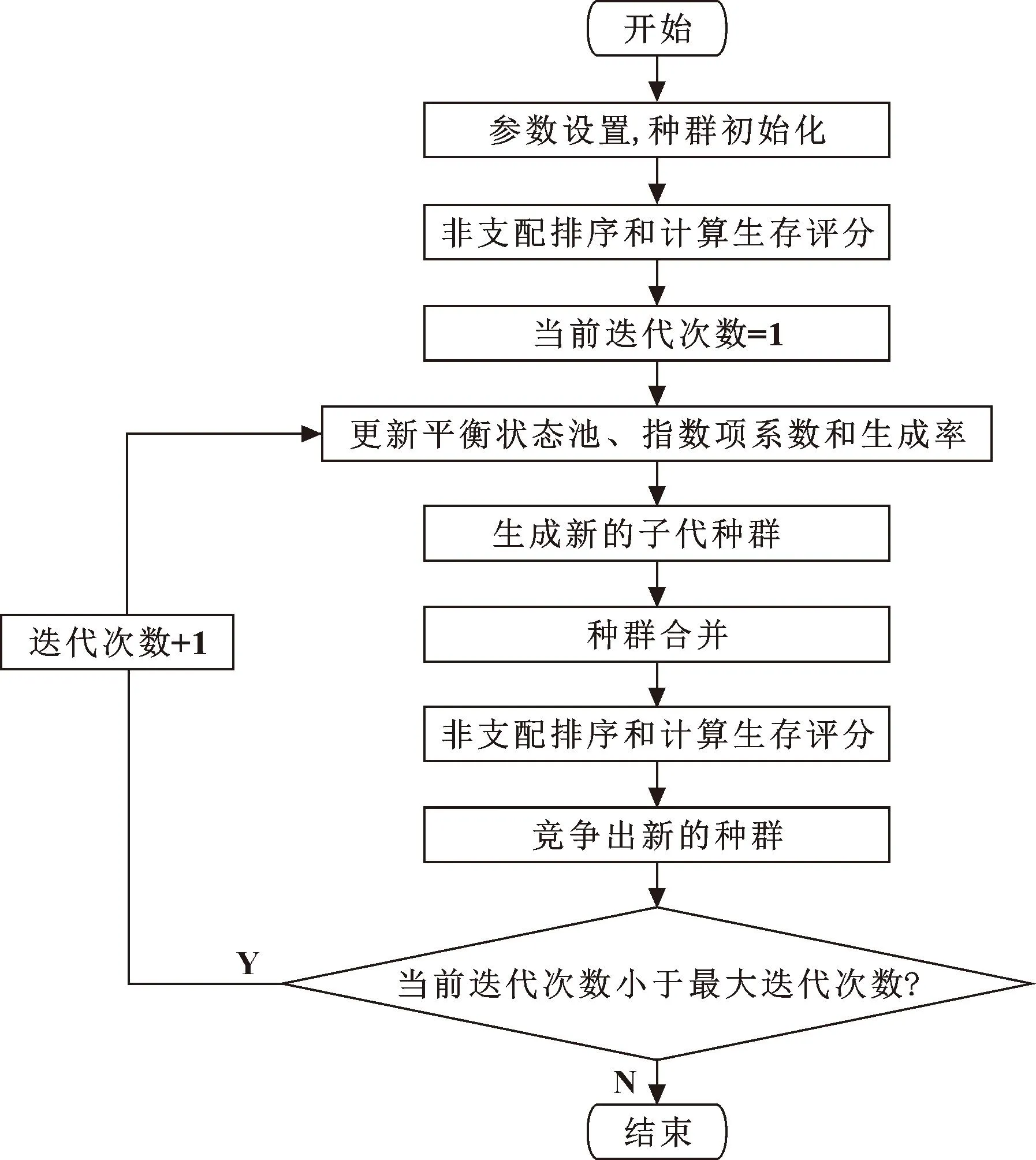
图3 DMONEO算法流程

4 实验验证与分析

为了验证所提出算法的性能，采用了TSP30、TSP50、TSP100这3个Mo-TSP问题进行测试，测试信息见表1。对比算法选取了NSGA-II[11]、SPEA2SDE[12]、IBEA[13]和MOEADD[14]。所有算法均采用相同的参数设置：种群规模N=200，最大迭代次数nmax=30 000；算法的其他参数设置均参考原文献。每个算法对每个测试问题独立运行30次。

表1 TSP基准测试函数

实验所用计算机环境为Intel Corei5-7300HQ@2.50 GHz CPU，16 GB内存，Windows10 64位操作系统。运行环境为MATLAB-R2019b。对比算法基于PlatEMO平台[15]。

本文作者使用超体积度量(Hypervolume，HV)以及算法的运行时间(Runtime)来衡量DMONEO算法和对比算法的性能。HV计算的是解集与参考点之间的目标空间体积。较大的HV代表着算法的表现更好，更接近真实的帕累托前沿和更好的多样性。运行时间体现了该算法的计算复杂度。

表2、3分别为DMONEO算法和其他对比算法在测试问题的HV统计结果和运行时间。性能指标平均值和标准方差作为评价标准，运行时间单位为秒(s)。带下划线的数据代表该算法在相应测试问题上表现最优。表格底部的数据是通过Wilcoxon符号秩检验的结果，以“+/-/=”的形式显示对应算法的表现优于/差于/接近DMONEO算法。

表2 基准测试实验HV值

根据表2所示的HV指标结果可得：DMONEO在Mo-TSP测试问题中均取得了最优的效果，MOEADD取得了两个次优值，NSGAII取得了一个次优值。平衡优化算法的平衡状态池可以视为算法的选择算子，对当前4个最优解以及平衡状态解的选择提高了算法的搜索能力。生存评分策略使算法在迭代过程中更好地保持多样性。表3所示的运行时间数据中，NSGAII取得了3个最优值，DMONEO取得了3个次优值。说明DMONEO算法融合了快速非支配排序策略，复杂度略大于NSGAII，但运行效率仍高于其他几个对比算法。综合表2、3的数据，DMONEO算法在Mo-TSP问题中得到的解接近真实的帕累托前沿，具有较高的多样性和效率性。

表3 基准测试实验运行时间

将DMONEO应用于实际问题中工件的焊点顺序规划问题。本文作者以47个焊点为例，表4为47个焊点在焊接时的坐标值和姿态值。表5、6分别为DMONEO算法和其他对比算法在47个焊点路径规划问题的HV统计结果和运行时间。

表4 47个焊点坐标和姿态值

表5 焊点规划实验HV值

表6 焊点规划实验运行时间

通过表5、6可得：DMONEO在实际焊接路径规划问题中取得了优异的表现，不仅取得了最好的HV指标值，并且运行时间也取得了最优值。

DMONEO算法得到的最优焊接序列为：17→34→16→20→12→25→27→11→5→24→6→38→40→42→35→41→31→30→2→3→39→1→32→22→36→26→14→29→15→4→43→21→8→9→33→7→13→28→44→45→46→47→18→19→37→23→10。

DMONEO算法在Mo-TSP测试和实际应用中都取得了较好的效果，说明该算法得到的解的多样性和效率性都较高。在实际生产中，技术人员可以为两个目标设定不同的权重，从解集中可以得到与权重相对应的最优焊接路径。

5 结语

本文作者针对点焊机器人的路径规划问题，以工作时间和长度路径作为优化目标，提出一种结合改进快速非支配排序策略的多目标平衡优化器算法——DMONEO。结合快速非支配排序策略，针对拥挤度因子不能很好地反映同层次解的密度的问题，通过生存评分来替换拥挤度因子，可以更好地保持种群的多样性。最后通过精英策略，将当前种群和子代种群合并竞争从而使得表现较好的个体保留。

通过TSP基准测试进行算法对比实验，结果表明本文作者提出的DMONEO算法相对于其他优化算法和改进算法均有较大的优势。最后，将提出的算法应用于点焊机器人的路径规划中，得到了较好的路径。未来进一步研究可以从以下几个方面发展：加入其他点焊机器人优化目标如能耗等，对点焊机器人的轨迹优化进行研究。