一类遗传概率计算问题的错因分析及解法探讨

方自超

(云南曲靖市第一中学)

利用遗传系谱图考查概率计算是高中生物学常见的考点之一,也是考查学生科学探究和科学思维等核心素养的重要手段,《普通高中生物学课程标准(2017年版2020年修订)》在模块2的学业要求中明确指出“学生能够运用统计与概率的相关知识,解释并预测种群内某一遗传性状的分布及变化”。在遗传系谱图中,子代条件的限定往往会导致子代本身或其亲本的样本空间发生改变,进而影响到概率计算,学生在确定样本空间范围或修正样本空间变化时常常出错,且对错误原因的认识不足。

1.子代条件限定对自身样本空间的影响及修正

1.1 例题展示

图1为某单基因遗传病的遗传系谱图,该遗传病受一对等位基因(A、a)控制,其中Ⅲ-1为杂合子的概率是

( )

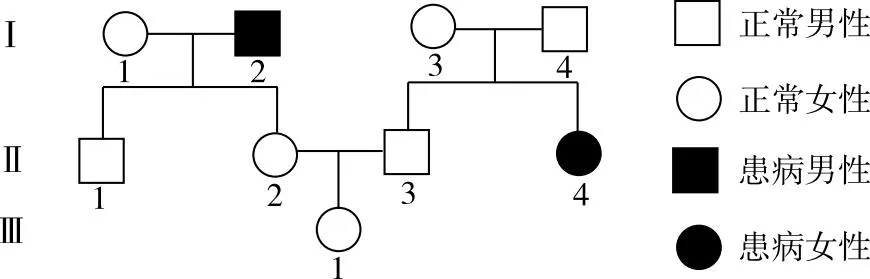
图1 某家系遗传系谱图

A.1/2 B.3/5

C.11/18 D.17/30

1.2 典型错解及错因分析

(1)典型错解

笔者用此题进行测试时发现,学生能够依据遗传系谱图判断出该病的遗传方式为常染色体隐性遗传,并能准确推断出Ⅱ-2的基因型为Aa,Ⅱ-3的基因型为1/3AA、2/3Aa。但在最后的计算结果中,错选A、C、D的学生却很多。

错解①:Ⅱ-2和Ⅱ-3可能的婚配方式有两种。Aa×1/3AA→1/3(1/2AA+1/2Aa)→1/6Aa;Aa×2/3Aa→2/3(1/4AA+2/4Aa+1/4aa)→1/3Aa。Ⅲ-1为Aa的概率为1/6+1/3=1/2,错选A。

错解②:Ⅱ-2和Ⅱ-3可能的婚配方式有两种。Aa×1/3AA→1/3(1/2AA+1/2Aa)→1/6Aa;由于Ⅲ-1不患病,其基因型不可能为aa,则Aa×2/3Aa→2/3(1/3AA+2/3Aa)→4/9Aa。Ⅲ-1为Aa的概率为1/6+4/9=11/18,错选C。

错解③:Ⅱ-2和Ⅱ-3可能的婚配方式有两种。Aa×1/3AA→1/3(1/2AA+1/2Aa)→1/6Aa;Aa×2/3Aa→2/3(1/4AA+2/4Aa+1/4aa)→1/6AA+2/6Aa+1/6aa,由于Ⅲ-1不患病,其基因型不可能为aa,去除1/6aa后得2/5Aa。Ⅲ-1为Aa的概率为1/6+2/5=17/30,错选D。

(2)错因分析

错解①的原因是审题不够仔细,没有注意“Ⅲ-1不患病”这一隐藏信息,误将aa个体考虑在样本范围内,错误确定了Ⅲ-1的样本空间范围。错解②③注意到了“Ⅲ-1不患病”这一隐藏信息,也考虑了将aa排除在样本空间范围之外,为了方便学生理解错误的原因,笔者利用数学模型还原了学生的解题思路。

错解②中,学生将Aa分别与AA、Aa婚配子代的理论比例视为两个独立的样本空间“1”(图2甲),去除Aa与Aa婚配子代理论比例这个样本空间“1”中的1/4aa后,修正了此样本空间“1”中AA和Aa的理论比例,再根据修正后的理论比例计算出Aa分别与1/3AA、2/3Aa婚配子代的实际比例(图2乙,“→”表示修正,括号内为基因型Aa的实际比例),从而计算出1/6+4/9=11/18的错误结果。该解法中,Aa与Aa的婚配子代理论上有出生基因型为aa个体的可能,但在计算实际比例前已去除子代中aa的理论比例并修正了AA和Aa的理论比例,表示Aa与2/3Aa的婚配子代中一定不会出生基因型为aa的个体,与理论推导相矛盾。

甲

错解③中,学生将Aa分别与1/3AA、2/3Aa婚配子代的理论比例视为两个独立的样本空间“1”(图3甲),去除Aa与2/3Aa婚配子代理论比例这个样本空间“1”中的1/6aa后,修正了此样本空间“1”中AA和Aa的理论比例进而得到实际比例(图3乙),从而计算出1/6+2/5=17/30的错误结果。该解法中,没有将Aa与1/3AA、2/3Aa的所有婚配子代视为一个样本空间“1”,去除1/6aa后仅在Aa与2/3Aa的婚配子代这个样本空间“1”中进行了比例修正,忽略了去除1/6aa后对Aa与 1/6AA 婚配子代这个样本空间“1”的影响。

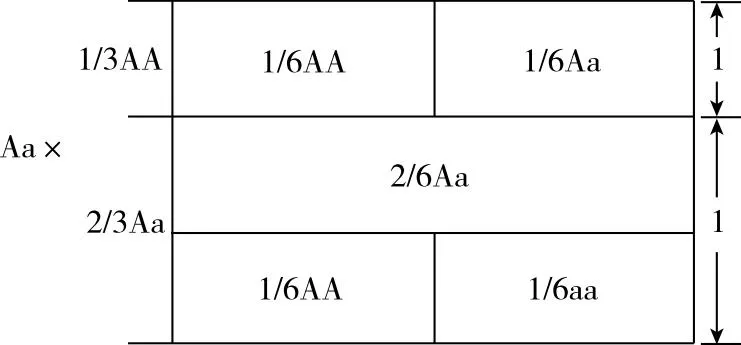
甲

1.3 解法探讨

(1)模型法

利用数学模型对错因进行分析后,学生意识到了1/3AA与2/3Aa属于一个样本空间“1”,Aa分别与1/3AA、2/3Aa的所有婚配子代也要视为一个样本空间“1”(图4甲),去除了2/3Aa与Aa婚配子代中的1/6aa后,要同时修正整个婚配子代样本空间“1”中所有AA和Aa的比例,从而计算出1/5+2/5=3/5的正确结果(图4乙)。

甲

(2)公式法

在明确求解范围是在“正常个体”这个样本空间中,也可用公式法进行求解。正常个体中Aa的概率=Aa的概率/正常个体的概率=Aa的概率/(1-aa的概率)。Aa的理论概率为上述错解①呈现的概率,即1/2,aa的理论概率为Aa×2/3Aa→2/3(1/4AA+2/4Aa+1/4aa)→1/6aa。因此,正常个体中Aa的概率=(1/2)/(1-1/6)=3/5。

(3)配子法

Ⅱ-2的基因型为Aa,产生的配子比为A∶a=1∶1;Ⅱ-3的基因型为1/3AA、2/3Aa,产生的配子比为A∶a=2∶1;Ⅲ-1基因型的理论比例为(A∶a)×(2A∶a)=2AA∶3Aa∶aa,由于Ⅲ-1的基因型不可能为aa,因此,Ⅲ-1基因型的实际比例为2AA∶3Aa,其中Aa的概率为3/5。

2.子代条件限定对亲本样本空间的影响及修正讨论

2.1 例题变式

图1为某单基因遗传病的遗传系谱图,该遗传病受一对等位基因(A、a)控制,若Ⅱ-2和Ⅱ-3再生一个孩子Ⅲ-2,Ⅲ-2表现正常的概率是________。

2.2 典型解法及讨论

(1)典型解法

Ⅱ-2的基因型为Aa,Ⅱ-3的基因型为1/3AA、2/3Aa,Ⅱ-2和Ⅱ-3可能的婚配方式有两种。Aa×1/3AA→1/6AA+1/6Aa,全部表现正常;Aa×2/3Aa→1/6AA+2/6Aa+1/6aa,有5/6的概率表现正常,故Ⅲ-2表现正常的概率为5/6。

(2)典型解法讨论

Ⅱ-2和Ⅱ-3先后生育的Ⅲ-1和Ⅲ-2并非两个独立事件,而是关联事件。在生育Ⅲ-2前,Ⅱ-2和Ⅱ-3已生育一个正常孩子Ⅲ-1,Ⅲ-1的出生会影响亲本中Ⅱ-3原本的基因型比例,进而影响到Ⅲ-2 为正常孩子的概率。因此,在计算Ⅲ-2相关概率前,需要依据Ⅲ-1的表型对Ⅱ-3的基因型比例进行修正。为了方便理解,笔者借助数学模型进行分析。

如图5所示,生育Ⅲ-1前,Ⅱ-3的基因型为1/3AA、2/3Aa,在子代样本空间“1”中,子代有1/3的可能由Ⅱ-3中的1/3AA决定且都表现正常,子代有2/3的可能由Ⅱ-3中的2/3Aa决定,其中有1/2正常、1/6患病。如图6所示,在Ⅲ-1出生后且表型正常的情况下,应去除子代样本空间中1/6患病的可能,新的样本空间由“1”变为了“5/6”,此时,若将新的样本空间由“5/6”重新修正为“1”,原来1/3正常的概率修正为了2/5且仍由AA决定,原来1/2正常的概率修正为了3/5且仍由Aa决定,因此,Ⅱ-3的基因型为AA的概率不再为1/3,应修正为2/5,基因型为Aa的概率不再为2/3,应修正为3/5,Ⅲ-2表现正常的概率应依据Ⅱ-3修正后的基因型比例进行计算。

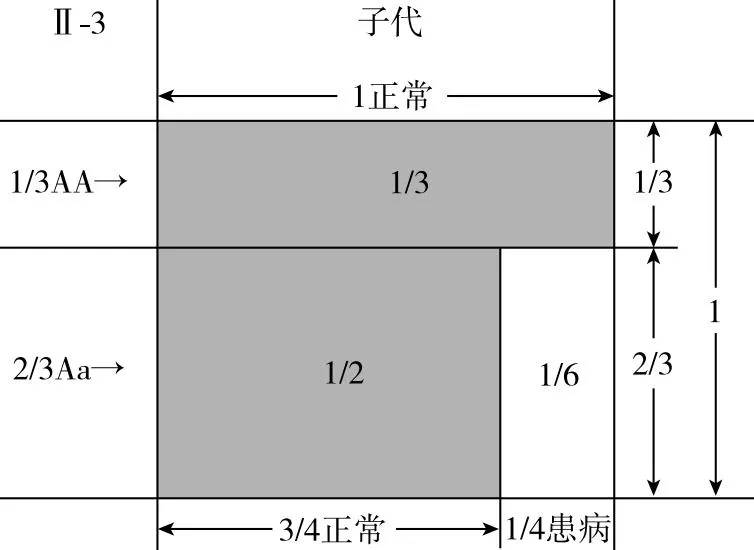
图5 生育Ⅲ-1前,Ⅱ-3的样本空间和子代的样本空间

图6 生育Ⅲ-1后,Ⅲ-1的样本空间和Ⅱ-3的样本空间

2.3 修正解法探讨

(1)模型法

通过对上述模型的分析,在生育正常的Ⅲ-1后,Ⅱ-3为AA的概率修正为2/5,为Aa的概率修正为3/5,Ⅱ-2的基因型仍为Aa。Aa×2/5AA→1/5AA+1/5Aa;Aa×3/5Aa→3/20AA+3/10Aa+3/20aa,故Ⅲ-2表现正常的概率为17/20。

(2)贝叶斯公式法

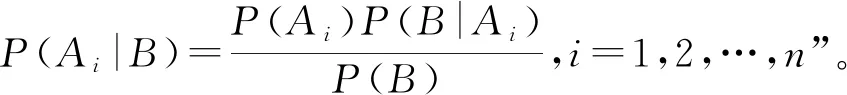
根据贝叶斯定律,将Ⅱ-2和Ⅱ-3的两种婚配方式视为事件A,A1表示AA×Aa,A2表示Aa×Aa,将他们生育正常孩子视为事件B,可得P(B|A1)=1、P(B/A2)=3/4。在生育Ⅲ-1前,已知Ⅱ-2的基因型为Aa,Ⅱ-3的基因型为1/3AA、2/3Aa,可得P(A1)=1/3、P(A2)=2/3,P(B)=5/6。在Ⅲ-1出生后且表型正常的情况下,可得P(A1|B)=2/5、P(A2|B)=3/5,即事件A1发生的概率修正为2/5,事件A2发生的概率修正为3/5,如表1所示。根据修正后的概率可得 Ⅱ-2 和Ⅱ-3再生一个孩子Ⅲ-2 表型正常的概率为17/20。

表 利用贝叶斯定律分析Ⅱ-3的基因型

3.小结

综上所述,在遗传系谱图中,子代条件的限定会直接影响到自身的样本空间,也会间接影响到亲本的样本空间。借助数学模型可以直观地帮助学生分析在确定样本空间范围和修正样本空间变化时产生的错误,让学生对自己的错误“知其然,更知其所以然”。