用好真题 把握本质 做好变式 提高素养——以解析几何部分试题为例

高阿龙

(北京市延庆区教育科学研究中心)

北京高考中,解析几何部分综合题目的考查,以直线和椭圆位置关系为主,往往思路比较简单,但重点考查学生数学运算核心素养,学生解题需要较长时间.提高学生数学运算核心素养,可以多找一些题目进行练习,同时教师和学生如果能够理解题目背后的命题背景和原理,进行适当的变形后再进行训练,才更能提高学科核心素养.

直线与椭圆位置关系部分,离不开交点、动点等问题.而当我们从高观点下看待一些题目时,比如利用射影几何的一些结论来分析问题,更容易发现问题的本质,方便对试题进行变式探究.

射影几何中有很多重要的结论,也是很多解析几何试题命制的基本背景和原理,本文从极点和极线以及帕斯卡六边形的相关结论中,分析2023年北京高考数学和模拟试题中解析几何解答题的命题背景,帮助教师和学生,了解试题的命制本质.首先,笔者以椭圆为例,介绍几条关于极点和极线以及帕斯卡六边形的相关结论.从给出任意一点P,得到其相应极线的方法谈起.

结论1点在椭圆外的情况:已知椭圆C所在平面上一点P(P在椭圆外),过P作两条直线PM和PN,分别与椭圆C相切于M,N,则直线MN就是点P的关于椭圆C的极线.

图1 结论1

图2 结论2

结论2点在椭圆上的情况:已知椭圆C所在平面上一点P(P在椭圆上),过P作切线l,则直线l就是点P的关于椭圆C的极线.

结论3点在椭圆内的情况:已知椭圆C所在平面上一点P(P在椭圆内),过P作两条直线AB和MN分别与椭圆C相交于A,B,M,N,延长AM和NB交于点H,延长AN和MB交于点E,则直线EH就是点P的关于椭圆C的极线,同时,直线PH是点E的关于椭圆C的极线,直线PE是点H的关于椭圆C的极线,△PEH叫做自极三角形.

图3 结论3

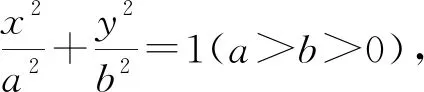
结论5帕斯卡六边形定理:如果一个二次曲线(高中学习阶段包括圆、椭圆、双曲线、抛物线)内有一个内接六边形ABCDEF,则三组对边的交点共线.

特殊情况:(1)当出现平行的对边时,则交点在无穷远处;

(2)当两点重合时(即六边形退化),重合点的连线为该点处的切线.

以上结论是射影几何中比较基础的结论,本文中就不再给出证明,下面我们用极点和极线以及帕斯卡六边形的相关结论来分析北京2023年高考试题,教师在设计教学时,可以根据真题给出相似难度的变式,提高学生的解题能力和数学运算核心素养.

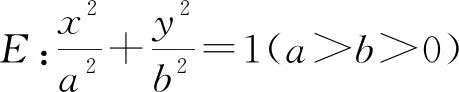
(Ⅰ)求E的方程;

(Ⅱ)设P为第一象限内E上的动点,直线PD与直线BC交于点M,直线PA与直线y=-2交于点N.求证:MN∥CD.

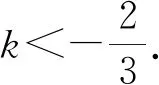
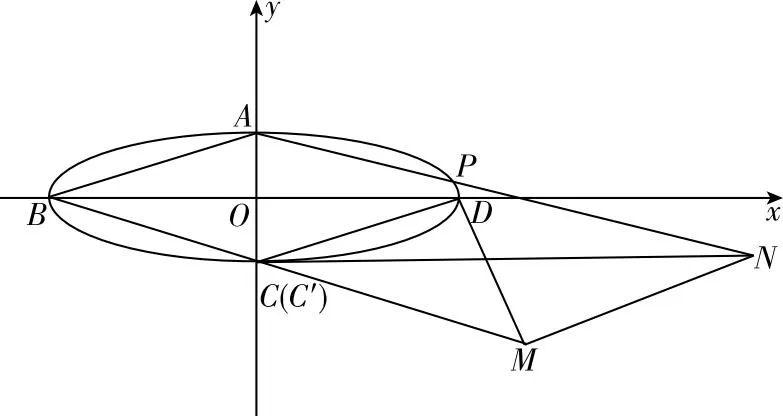
图4

【试题背景分析一】帕斯卡六边形退化为五边形的形式

本题中直线y=-2可以看成是在点C处的切线方程,我们可以理解为椭圆内接六边形是PDCC′BA,其中PD与直线BC交于点M,直线PA与直线y=-2(即CC′)交于点N,剩余的对边AB与CD平行,可以理解为交点在无穷远处设为H,根据帕斯卡六边形定理可知:H在直线MN上,也就是说直线MN和CD在无穷远处相交,所以MN∥CD.根据这个本质,我们可以从以下几个角度对试题进行变形.

【变形一】改变椭圆的方程

我们用更一般的形式来表述这个题目如下:

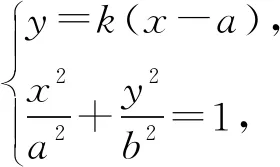
这个变式里,具体的椭圆的方程可以任意给出数值,本变式从图形结构和解题步骤上来说,和高考真题完全一致,可以在分析高考题后,让学生进行练习,重点在培养学生的数学运算核心素养,从而突破教学的难点.

【变形二】改变退化点的位置

在真题中,退化点的位置是在C点,我们可以把退化点放在B,A,D处,如放在点A处.

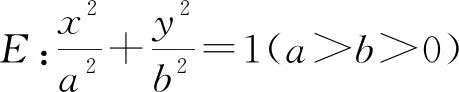
(Ⅰ)求E的方程;

(Ⅱ)设P为第三象限内E上的动点,直线AD与直线BP交于点N,直线PC与直线y=2交于点M.求证:MN∥CD.

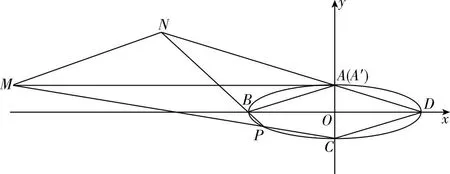
图5

这个变形,我们改变了图形的结构,但是最终直线MN的斜率还是没有变化.

【变形三】改变两条平行线的位置

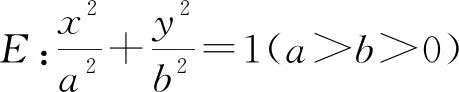
(Ⅰ)求E的方程;

(Ⅱ)设P为第四象限内E上的动点,直线PC与直线AB交于点N,直线PD与直线x=-3交于点M.求证:MN∥BC.

图6

在例1中,平行的两条直线是AB与直线CD,此处换成了AD与直线BC平行.

以上三个试题的变形是在帕斯卡六边形的背景下,进行的变式,通过变式训练,学生可以更好地掌握这类单动点导致其他交点位置改变的数学运算的问题.

【试题背景分析二】极点极线的形式

以极点极线作为命题背景,可以分析如下:

图7

根据上面的分析,本题可以作如下变式训练:

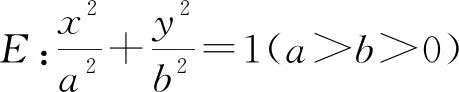
(Ⅰ)求E的方程;

(Ⅱ)设P为第一象限内E上的动点,直线PD与直线BC交于点M,直线BP与直线CD交于点H,直线PA与直线y=-2交于点N.求证:MH⊥CN.

再分析一道北京的模拟试题,体会利用极点极线的方法分析试题背景,进行变式训练的方便.

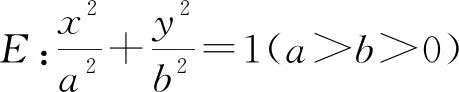
(Ⅰ)求椭圆E的方程;

(Ⅱ)设斜率为k的直线l与x轴交于点P,与椭圆E交于不同的两点M,N,点M关于y轴的对称点为M′,直线M′N与y轴交于点Q.若△OPQ的面积为2,求k的值.

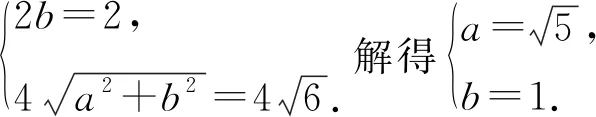
通过上面的分析,利用极点极线可以发现本题的本质:极点Q的极线垂直y轴且过点T,而且通过题目中面积的关系可以得到极点Q与点P的关系,通过这个本质,我们可以把题目作如下变式:

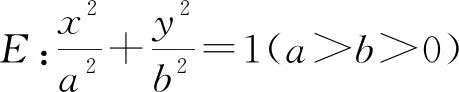
(Ⅰ)求椭圆E的方程;

(Ⅱ)设斜率为k的直线l与x轴交于点P,与椭圆E交于不同的两点M,N,点M关于y轴的对称点为M′,直线M′N与y轴交于点Q.求证:|OP||OQ| 是定值.

分析：变式把握了问题的本质,即点Q作为极点,对P的坐标以及直线的斜率k,都有直接的联系,最终会消掉变量,得到定值.

高考题目中,很多关于直线与圆锥曲线的综合题目,离不开直线与圆锥曲线相交产生两个交点以及顶点,这样试题往往带有极点和极线以及帕斯卡六边形的背景,也成为不少试题命制的主要依据,在平时教学和学习中,一些高考题目通过高观点下分析其本质,在此基础上,为学生进行变式训练.通过经典题目及其变式的训练,为发展数学学科的核心素养提供了很好的学习素材.