漫谈黄金分割
黄 雨 樊 涛
(安徽省淮南第二中学)
0.618是一个令世界震惊的数字,在其中隐含着最美的比例,人体、雕塑、绘画、图形、建筑等,只要有优美的外观,必然蕴含着这个数字,因此,人们将其称为黄金分割比例(简称黄金分割),它是数学大厦上一颗璀璨的明珠.
世人皆知,几何学里有两件瑰宝,一是勾股定理,二是黄金分割.有人说:“如果把勾股定理比作黄金矿的话,那么可以把黄金分割比作钻石矿”,当见黄金分割意义非凡.
一、黄金分割的由来
传说两千多年前,古希腊数学家毕达哥拉斯(Pythagoras,约公元前580年~约前500年)走在街上,当路过一个铁匠铺时听到“叮当、叮当……”的打铁声,一长一短,非常悦耳,于是驻足倾听.他发现声音的节奏具有规律性,凭数学家的天赋,他把这种声音的比例用数学的方式表达了出来.公元前4世纪,古希腊数学家欧多克索斯系统地研究了这一问题,并建立起了比例理论.后来,数学家欧几里得吸收了欧多克索斯的理论,并将其撰写在《几何原本》中,使得比例理论得到了进一步的发展.我国著名数学家华罗庚推广优选法,其中最著名的就是0.618法,也称黄金分割法.
1.1 黄金分割比的定义
如图1,把一条线段分成两段,如果较短的一段与较长的一段的比等于较长的一段与整条线段的比,那么这个比值就是黄金分割比.

图1

1.2 黄金分割点的作法


图2(1)
②如图2(2),以D为圆心,以BD为半径作圆D,交AD于E点;
③如图2(3),以A为圆心,以AE为半径作圆A,交AB于C点,则C即为黄金分割点.
1.3 黄金矩形的作法
①如图3(1),在正方形ABCD中,取AB的中点E,连接EC;

图3(1)
②如图3(2),以E为圆心,以EC为半径作圆E,交AB的延长线于F点;
③如图3(3),以BC,BF为邻边构造矩形BCGF,则矩形ADGF,BCGF都为黄金矩形.
二、黄金分割的发展
2.1 从斐波那契数列到黄金分割
意大利数学家列昂纳多·斐波那契(Leonardo Fibonacci),生于公元1170年,卒于1250年,出生于比萨,他被人称作“比萨的列昂纳多”.他在建立养兔场的兔子演化模型时发现了数列{Fn}:1,1,2,3,5,8,13,21,34,55,89,144,….满足从第三项起,每一项都是前两项之和,即:Fn+2=Fn+1+Fn(n∈N*),此数列称为斐波那契数列,戏称兔子数列.

(1)数字特征
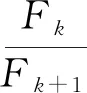
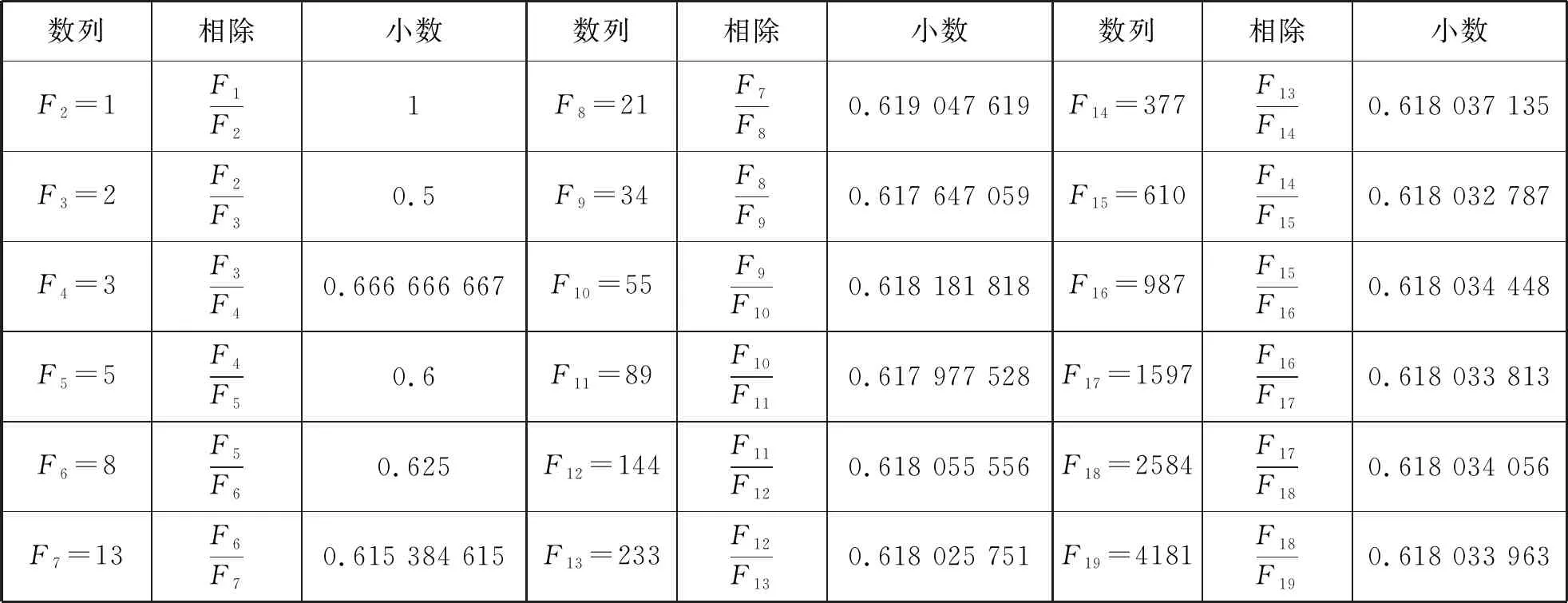
数列相除小数数列相除小数数列相除小数F2=1F1F21F8=21F7F80.619 047 619F14=377F13F140.618 037 135F3=2F2F30.5F9=34F8F90.617 647 059F15=610F14F150.618 032 787F4=3F3F40.666 666 667F10=55F9F100.618 181 818F16=987F15F160.618 034 448F5=5F4F50.6F11=89F10F110.617 977 528F17=1597F16F170.618 033 813F6=8F5F60.625F12=144F11F120.618 055 556F18=2584F17F180.618 034 056F7=13F6F70.615 384 615F13=233F12F130.618 025 751F19=4181F18F190.618 033 963
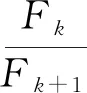
(2)理论证明
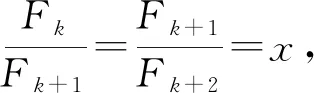
方法二:Fn+2=Fn+1+Fn,根据递推数列的解法,建立方程,利用根来构造数列.
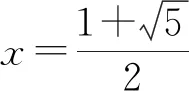



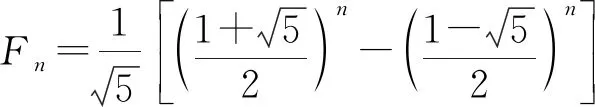
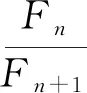

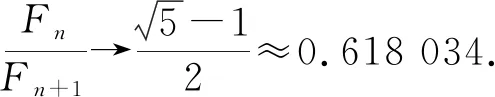
2.2 从斐波那契螺旋线到黄金分割比例构图
生活中我们能够观察到芭蕾舞演员会踮起脚尖舞蹈,女生喜欢穿高跟鞋,著名雕像被故意延长了双腿,摄影师构图会把主体物放在旋涡中心.这些举动是否有科学依据,笔者带着疑问来研究斐波那契螺旋线.
(1)图形特征
分别以斐波那契数为边长作正方形,然后将它们拼成矩形,在每个正方形中画一个90°的扇形,连起来的弧线就是斐波那契螺旋线,又称黄金螺旋线,拼成的矩形近似为黄金矩形.如下图4(1)所示.

图4(2)

图4(3)
(2)黄金构图
摄影师会把主体物放到旋涡中心点(图4(2)),让其他的辅助画面围绕黄金螺旋线.世界名画《蒙娜丽莎的微笑》(图4(3))也是用黄金分割比例构图的.从它们身上发现,优美的构图其实就是在整体和局部反复地使用黄金分割.黄金分割具有比例性、艺术性、和谐性,蕴含着丰富的美学价值,即是美的密码.
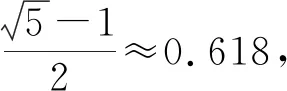
三、试题中的黄金分割
3.1 高考试题
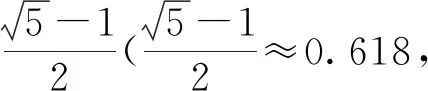
( )
A.165 cm B.175 cm
C.185 cm D.190 cm
【分析】根据黄金分割比,作出头顶、咽喉、肚脐、足底的简图.
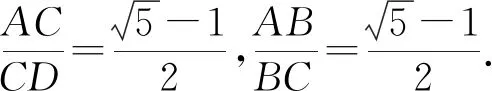

图5(1)

图5(2)

图5(3)
【点评】本题以最美人体为背景,考查了黄金分割、估算以及不等式等必备知识,考查了逻辑思维能力、运算求解能力、创新能力等关键能力,引导教学注重培养数学运算和逻辑推理核心素养.难点在于从两个不同的角度进行估算运算,考查创新能力.
【变式1】(背景同上题)某女生头顶至咽喉的长度为25 cm,肚脐至足底的长度为103 cm,肚脐以上满足黄金分割比例,则该女生应选择多高的鞋子,才能最接近满足上述两个黄金分割比例
( )
A.2 cm B.3 cm
C.4 cm D.5 cm

【点评】高跟鞋的选择是有科学依据的,并不是越高越好,要从审美的角度进行分析.

( )

图6
A.29 m B.29.8 m
C.30.8 m D.32.8 m
【分析】由矩形ABCD和EBCF是黄金矩形,由边长的比求出AB范围.
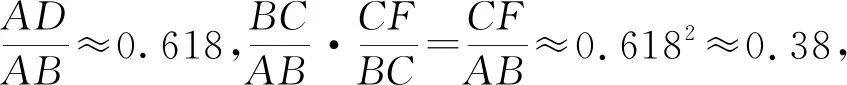
【点评】本题以黄金矩形为背景,考查黄金分割、估算、不等式等必备知识,考查了逻辑思维能力、运算求解能力、创新能力等关键能力,引导教学注重培养数学运算和逻辑推理核心素养.难点在于从两个不同的角度进行估算运算,考查创新能力.

( )

图7

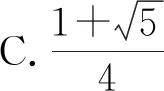
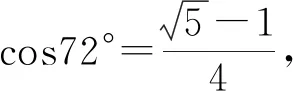

故选C.
【点评】本题以黄金三角形为背景,考查利用二倍角公式以及诱导公式求值等必备知识,考查了逻辑思维能力、运算求解能力等关键能力,引导教学注重培养数学运算和逻辑推理核心素养.
3.2 命题导向
以实际问题为背景,考查必备的基础知识,强调知识之间的内在联系,引导学生建立完备的数学知识体系.考查逻辑思维能力、运算求解能力、创新能力等关键能力,引导教学注重培养核心素养和数学能力.

