析真题 引教学 育素养
——以2023年全国甲卷理科第12题为例
邢铁军
(甘肃省酒泉中学)
1.真题呈现
( )

2.解法探究




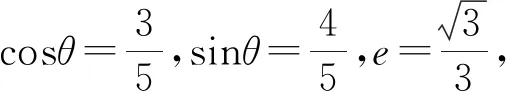



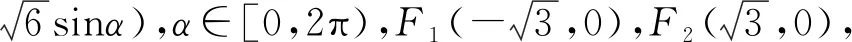

【点评】从本质讲,解法1、2、3、7属于同种解法,即求出点P的坐标,利用两点间的距离公式求出|OP|,但求点P坐标的途径不同,解法1属于通法,解法2利用椭圆焦点三角形面积的一个二级结论,解法3利用焦半径公式,解法7利用椭圆的参数方程.解法4利用中点的向量参数式方程,解法5利用向量极化恒等式的三角形模式,解法6数形结合法,充分利用椭圆的对称性和平行四边形的性质.结合本题客观题的属性,解法2、3、4、5、6都运用了解析几何中常用的二级结论,从中我们可以看出在客观题中充分利用一些常用的二级结论会使问题变得简单、运算变得简洁,避免“小题大做”的弊端,符合客观题“小题小做、小题巧做、快速得分”的思路.
“不同工业通信协议的时代已经一去不返。”贝加莱战略与创新副总裁Stefan Schonegger如是说道。
3.拓展推广


4.几点启示
2023年全国甲卷理科的第12题,打破往常选择题导数压轴的惯常,难度降低,特别对中档学生利好,使得大部分学生敢想敢做能做,起点低、思路广、方法多,通过多种方法探究,深度剖析试题的内涵价值,对于指导和引领数学日常教学与高考备考复习都有积极作用.
4.1 基础知识阶段教学应立足教材,重视概念教学
概念是数学学习的起点,只有正确形成概念,方能掌握和运用数学知识.教材是知识、方法、思想的重要载体.在解析几何基础知识的教学中,应以教材为主,摒弃丢掉教材、教辅资料为主的教学形式.重视概念教学,其一要重视概念的形成过程,注重为学生理解概念创设情景,如在解析几何教学中,课堂应留空白,采取学生亲自动手实验或信息技术手段画出椭圆、双曲线和抛物线,让学生体会曲线的形成过程,掌握获得曲线的基本活动经验,为深刻认识各种曲线提供直观感觉,培养学生直观想象核心素养;其二,要重视相近概念之间的区别和联系,感悟数学的整体性,如三大曲线的统一定义中的相同点和不同点,培养学生逻辑推理核心素养;其三,数学中的任何定义都是可逆的,既要重视概念的正面理解更要重视概念的逆用,解析几何中利用概念解题是首要掌握的,例如2022年全国乙卷第5题、第11题、2021年全国甲卷第5题、2022年全国甲卷第20题都是直接考查抛物线、双曲线的定义问题.
4.2 深化和升华典型例题和习题的价值功能
从近年高考试题看,教材是产生高考题的主要来源,相当数量的高考题源于教材,即使是综合题,也是基本题整合、加工而成.基础知识教学阶段,应该以典型例题、习题为主要解题教学对象,充分发挥例题的示范功能,同时挖掘习题背后隐藏的潜在价值,串联例题、练习、习题和复习题四个试题板块,引导学生利用归纳、整合等基本逻辑方法将其归类,如在平面解析几何中可归类为概念类、标准方程类、中点弦类、离心率类、直线与曲线的位置关系类等,特别注意试题中蕴含的二级结论及其推导过程,寻找共性、掌握通法,深挖蕴含的数学思想,从而顺应现行高考“反套路、机械刷题”的思路.
案例1:探究椭圆的产生方式

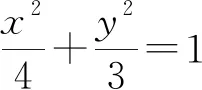
(1)求动点M的轨迹方程,并指出随m变化时方程表示的曲线C的形状.
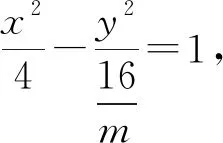
通过课本一个例题和一道习题的教学,其一,引导学生准确认识不同曲线,从不同角度理解椭圆概念,提高学生的数学运算、直观想象、逻辑推理核心素养;其二,渗透分类讨论等数学思想;其三,引导学生总结除椭圆定义外,产生椭圆的其他形式,进一步有:

定义3:平面内到两定点A(-a,0)和B(a,0)连线的斜率之积为m,当m<0且m≠-1时,表示焦点在x轴上除去这两点的椭圆.
通过纵向串联例题和习题的教学我们得到椭圆的另外两种产生方式,分别叫做椭圆的第二、第三定义.例如2009年全国高考数学文理科第20题(琼、宁卷)、2013年全国卷Ⅰ理科第20题(文科第21题)、2013年大纲卷理科第8题、2013年陕西文科第22题、2019年全国Ⅰ理科第10题、2022年高考全国甲卷数学理科第10题等都是以椭圆的三个定义为背景命制的高考题.
4.3 重视经典问题
纵观历年解析几何部分的高考试题可以看出,高考从不回避经典,“定义、焦点三角形、中点弦、垂径定理、极点极线、阿基米德三角形”等问题常考常新.题在书外,根在书内,这些经典知识教材中或以例题出现或以习题出现,或以阅读形式出现,教学中一定要重视对这些经典问题的研究和积累,让学生理解掌握经典问题的知识背景,通过变式探究、特殊到一般、拓展延伸等路径进行归纳总结让一些知识形成定理作为二级“结论”积累下来使用.如解法2中焦点三角形的面积公式、极化恒等式等都可由课本例题或习题探究得到.
案例2:探究椭圆中的垂径定理


以该知识点为背景的高考试题有2013年新课标Ⅱ卷理科第20题、2015年新课标文科Ⅱ第20题、2015年新课标Ⅱ理科第20题等.
4.4 重视向量工具的使用
平面向量作为数形结合思想的典范,架起了代数与几何的桥梁,在解析几何教学中要充分利用向量工具性的作用,加强与向量的融合,利用等价转化思想将问题转化为向量问题,利用向量的几何性质或者代数运算解决问题,如证明线段垂直可转化证明对应向量垂直、夹角(锐角、直角、钝角)问题可利用向量的数量积解决、直线恒过定点可利用直线的向量参数式方程或向量定比分点公式等证明.
4.5 重视多解探究和变式教学
解题教学中应注意多解探究,在多解探究和变式教学中注意以下几个方面:一是例题的典型性,可选择真题中的典型试题开展;二是重视过程分析,重点引导学生思考破题视角和思路分析及思维训练;三是注重总结复盘,包括条件转化方法、模型构建方法、运算简化方法等,对比不同方法的优势与不足,让学生掌握各种方法的使用思路,达到快速准确解题.
总之高考真题是命题者智慧和心血的结晶,教材是知识的主要载体,在双减、反机械刷题等政策的大背景下,充分研究真题、探究真题与教材的联系,对于一线教学具有重要的启示意义.

