巧作辅助线 活解压轴题

杨菲雯

1 真题呈现

（2021年常德市中考数学第26题）如图1，在△ABC中，AB=AC，N是BC边上的一点，D为AN的中点，过点A作BC的平行线交CD的延长线于点T，且AT=BN，连接BT.

（1）求证：BN=CN;

本题作为中考压轴题，存在一定的难度.本题共三问，由于前两小问较易，答案以简析方式呈现，具体解法以第（2）问的第②小问为主.

2 证法探究

2.1 第（1）问与第（2）①问证法简析

对于（1），如图1，在△ADT与△NDC中，D是AN的中点，则AD=ND.由AT∥BC，可得到∠ATD=∠NCD，∠ADT=∠NDC，则△ADT≌△NDC，所以AT=NC.又因为AT=BN，所以BN=CN.

对于（2）①，如图3所示，因为点N关于边AC的对称点是M，所以CN=CM，而TA=NC，所以TA=CM.由（1）知AN是等腰三角形ABC的高，且AT∥BC，所以∠TAO=90°.因为N关于边AC的对称点是M，则∠ACN=∠ACM.因为OA=OC，则∠NAC=∠OCA，所以∠MCO=∠ACM+∠OCA=∠NCA+∠OCA=∠NCA+∠NAC=90°，所以∠TAO=∠MCO=90°.

综上可知，△TOA≌△MOC（SAS），则OT=OM，即△OTM是等腰三角形，且∠TOA=∠MOC，所以∠TOA+∠AOM=∠MOC+∠AOM，即∠TOM=∠AOC，即等腰三角形TOM与等腰三角形AOC的顶角相等，所以它们的底角相等，故△TOM∽△AOC.

2.2 第（2）②问证法探究

（ⅰ）执果索因，初审条件

（ⅱ）直接证全等，探究失败

笔者通过观察，令OM与AC相交与点S，尝试证明△TAP≌△MSP，以此证明TP=PM.要证△TAP≌△MSP，即证TA∥SM且TA=SM，即证SM∥NC.笔者分析已知条件，始终无法证得SM∥NC，因此探究失败.于是猜想SM与NC不存在平行关系.

（ⅲ）联想辅助线，解法生成

思路1：巧作平行证全等.

依据分析，解法生成.过点M作NC的平行线，构造全等三角形，以此证得P为MT的中点.

思维发散，一法多用，重作平行证全等.证法一是作平行线，构造中心对称型全等三角形（△TAP与△MQP关于点P中心对称），提出猜想，以点P为旋转中心，构造关于△CMP的中心对称型全等三角形，顺势联想到过点T作关于MC的平行线.

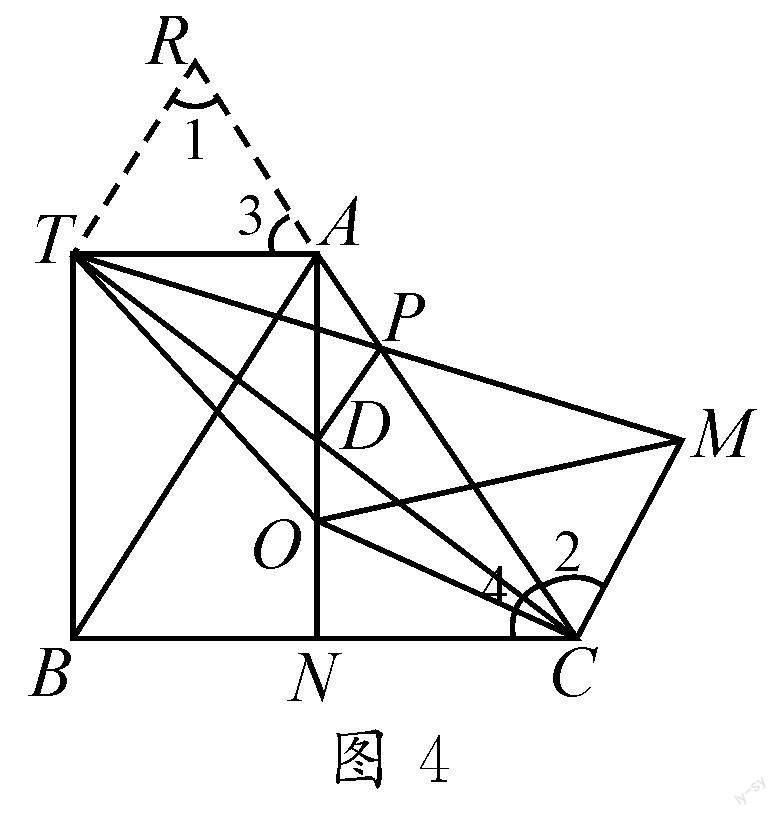
證法二：如图4，过点T作TR∥MC交CA的延长线于点R，则∠1=∠2.由TA∥NC，得∠3=∠4.而

思路2：绕点旋转推出平行.

大道至简，殊途同归.绕点旋转证平行.由思路1可以联想，将CM绕点M顺时针旋转，使点C落在点E上，由等腰对等角与轴对称可以推导出EM∥NC∥TA.

证法三：如图5，将CM绕点M顺时针旋转，使点C落在点E上，连接AM，TE.可参照思路1的证明思路证得P是TM的中点.这里给出新的证明方法.因为EM=CM=AT，所以∠MEC=∠MCE.因为∠CAN+∠ACN=90°，所以∠CAN+∠ACM=90°，即得到∠TAN+∠NAC+∠ACM=180°，因此∠TAC+∠ACM=180°.又因为∠AEM+∠CEM=180°，所以∠TAC=∠AEM，证得AT∥EM，则四边形ATEM是平行四边形，可得TP=PM.又因为TD=DC，所以PD∥CM，

思路3：活用翻折证中点.

切换视角，窥探新法，利用对称作辅助线.连接NP，NM，显然NP=NM，若能证明TP=NP，即可解决疑难.于是连接TN，利用等角对等边证明TP=NP.

证法五：如图6，连接NP，NM，NT.由M，N关于AC对称得到MN⊥AC，PN=PM，则∠1=∠2.由TA∥NC且TA=NC，得到四边形ATNC是平行四

思路4：四点共圆证垂直.

打破常规，别出新意，利用辅助圆思想巧妙解题.由第（2）①知OT=OM，要证明P是TM的中点，根据等腰三角形“三线合一”的性质，连接OP，若能证得OP⊥TM，即可解决问题.通过观察∠TAO=90°，联想到四点共圆的判定（同底且同侧顶角相等的两个三角形的顶点共圆），显然∠OTP与∠OAP所在的三角形同底且两角在OP的同侧，于是得到点O，T，A，P四点共圆.

证法六：如图7，连接OP.由（2）①知△TOM∽△AOC，则∠OTM=∠OAC，由四点共圆的判定得到点T，A，P，O四点共圆.由已知TA∥NC，NC⊥AN，得TA⊥AN，即证得OP⊥TM.又因为OT=OM，所以P是TM的中

3 解后反思，教学建议

（1）抓住图形特征，渗透几何思想

四边形出题灵活，难以联想作辅助线的方法，不同类型问题的解题方法不同.如本试题依托矩形、等腰三角形、轴对称等相关知识点，因此解题方法灵活多样.依据题意，学生不难得出要证P是TM的中点，但是联想作辅助线存在一定的难度.学生对图形特征把握不透彻，相关性质定理无法达到灵活运用的层次.

（2）剖析问题类型，归纳问题解法

几何压轴题主要考查学生的综合运用能力，学生对几何图形相关性质定理的掌握程度关乎解题思路的拓展.以本试题为例，通过轴对称指引学生构造平行，又根据等腰三角形“三线合一”的性质，推知证明OP是TM的中垂线，顺势联想到四点共圆的判定定理，容易得证.

（3）培养数学思维，提升解题能力

学生解题能力的提升是建立在夯实基础、灵活运用的基础上的，教师在教学过程中要注意培养学生的联动思维，出题、解题不局限于当下的某些方法，而是引导学生通过观察，启发思考.几何综合解题能力的提升不能一蹴而就，八年级是打基础，做提升的关键阶段，教师可在八年级时给学生训练中考压轴题，在培养学生解题能力的同时注意知识体系的搭建.