装配式变电站钢框架梁截面选型与优化研究

张 振，李 腾，聂建春，张 前，王 旭

(1.内蒙古电力( 集团)有限责任公司，内蒙古 呼和浩特 010020；2.中国能源建设集团浙江省电力设计院有限公司，浙江 杭州 310012；3.内蒙古电力( 集团)有限责任公司内蒙古电力经济技术研究院分公司，内蒙古 呼和浩特 010020)

0 引言

建筑工业化、模块化建设是我国建筑行业的发展方向。近年来，我国大力推行装配式建筑，电网公司提出建设装配式变电站的要求，220 kV 及以下变电站建(构)筑物均优先采用装配式结构。钢结构以其工业化程度高、湿作业少、施工周期短等特点，已成为装配式变电站建筑的主要结构形式。但相较于传统的钢筋混凝土结构，钢结构工程造价较高，降低钢结构造价有利于推进钢结构在变电站中的应用。

《混凝土结构构造手册》[1]建议钢筋混凝土框架梁的高跨比取为1/15 ～1/10。JGJ 3—2010《高层建筑混凝土结构技术规程》[2]建议框架结构的主梁截面高度按计算跨度的1/10 ～1/18 确定。而GB 50017—2017《钢结构设计标准》[3]和《钢结构设计手册》(第四版)[4]未对钢框架梁的高跨比做出明确规定。钢结构设计时，设计人员选取不适当的截面容易造成浪费；或者需进行多次试算、调整，从而造成工作量增加。若能明确钢框架梁的高跨比，将大幅减少设计人员的工作量、节省用钢量。本文对变电站钢结构优化设计进行研究，充分利用截面的力学特性，探索变电站钢框架梁的高跨比，从而达到减少用钢量、降低造价的目的。

1 模型简化

钢框架结构空间分隔灵活、结构整体性好，广泛应用于变电站建筑结构。变电站钢框架结构与民用建筑钢结构相比，具有布置受工艺影响大，跨度大、空间大，层数少、常规工程均为2 层以内，受地震和风荷载影响小，楼面活荷载大、变形敏感等特点[5]。竖向荷载和变形往往是钢框架梁结构设计的控制因素。

变电站建筑层数少，底层钢框架柱轴压比一般小于0.40，根据GB 50011—2010《建筑抗震设计规范》[6]可不考虑“强柱弱梁”对钢框架梁截面的调整。为方便研究，本文对受力模型进行简化，取一榀框架并简化为等截面刚架模型。梁柱连接、柱脚均采用刚接，框架柱采用箱型截面，框架梁采用H 型钢，钢材选用Q355B。忽略地震和风荷载影响，仅考虑承受均布竖向荷载。钢框架受力简化模型如图1 所示。

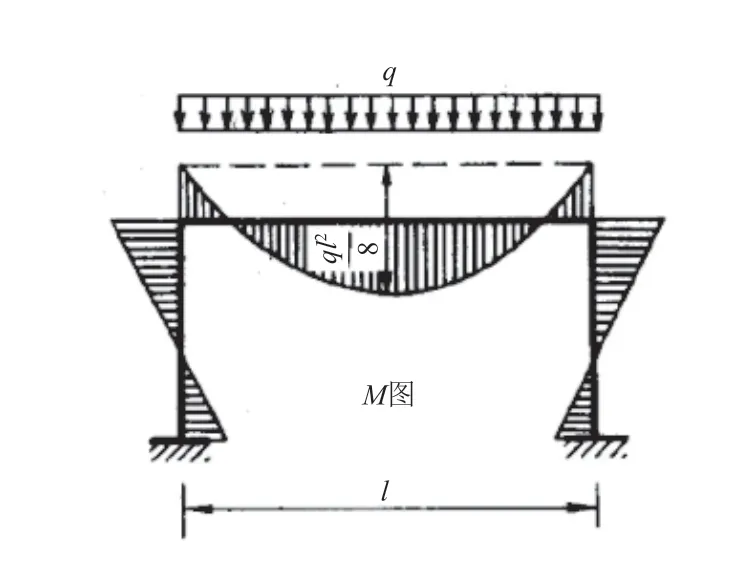
图1 钢框架受力简化模型图

按照变电站钢结构弹性方法设计，不考虑钢框架梁、柱塑性发展。根据现行钢结构设计标准[3]，梁柱截面板件宽厚比等级不应低于S4 级。

钢框架梁截面惯性矩Ix可反映其受弯性能，H 型钢梁高h、梁宽b、翼缘厚度tf和腹板厚度tw，均可不同程度影响梁的抗弯性能。其中，梁高h对H 型钢梁抗弯性能影响最为显著。而当梁高增加Δh时，梁截面积仅增加Δh·tw，相较于其他因素，用钢量增加最少。

因此，本文着重研究梁高对钢框架梁受力性能影响，以焊接H 型钢[7-8]为例进行分析。

2 刚架模型静力分析

2.1 按承载力极限状态分析

根据《建筑结构静力计算手册》[9]中的刚架内力计算公式，推导出受均布线荷载的钢框架梁的支座弯矩标准值计算式为：

在均布荷载作用下，梁跨中弯矩和支座弯矩总和等于ql2/8。因此，得到跨中弯矩标准值计算式为：

式中：M1、M2分别为梁左右两端支座弯矩标准值；M0为梁跨中弯矩标准值；K为梁、柱线刚度比。

跨中弯矩与支座弯矩绝对值相等时，则：

求得K=2/3，此时钢框架梁弯矩设计值有最小值，梁截面最小，用钢量最省。

2.2 按正常使用极限状态分析

根据《建筑结构静力计算手册》[9]中的单跨梁挠度计算公式，钢框架梁的两端约束条件介于简支和嵌固之间，因此，钢框架梁的跨中挠度也介于简支梁和嵌固梁跨中挠度之间，跨中挠度v计算式为：

式中：β与梁、柱线刚度比相关常数，且1 ≤β≤5；嵌固时，β=1，简支时，β=5；E为钢材弹性模量；Ix为对X轴的截面惯性矩。

当梁柱线刚度比K为定值时，β是与K有关的常数，数值上等于钢框架梁跨中挠度与两端嵌固梁跨中挠度比值。因此，可通过有限元法分别建立钢框架梁和两端嵌固梁模型，计算跨中挠度比求得β。

有限元模型取柱高为5 m，梁跨度分别取5 m、8 m 和10 m，梁柱线刚度比K取2/3。其中梁跨度为8 m 的模型如图2 和图3 所示。在相同荷载条件下，不同跨度梁跨中挠度结果见表1所列。

表1 不同跨度梁β值计算结果

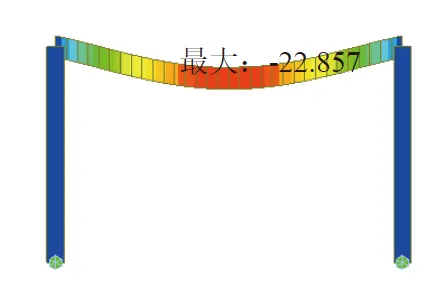
注：梁挠度数据单位为mm图2 钢框架梁跨中挠度

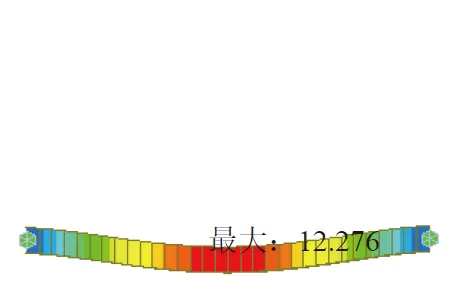
注：梁挠度数据单位为mm图3 两端嵌固梁跨中挠度

根据计算结果，对不同梁截面和跨度，当K=2/3 时，β呈高度近似性，可近似取为1.87。

综上所述，梁、柱线刚度比K在2/3 附近时，梁跨中弯矩和支座弯矩绝对值接近，弯矩设计值最小，按承载力极限状态计算的梁截面最优；此时钢框架梁跨中挠度与两端嵌固梁跨中挠度比值β近似为1.87。

3 钢梁临界高跨比

钢梁截面设计应满足承载力、变形、整体稳定性和局部稳定性的要求。梁顶设置栓钉与上部楼板牢固连接，有效阻止了受压翼缘的侧向位移，故可以不计算钢梁的整体稳定性；通过限制板件宽厚比和加设加劲肋的方式，满足局部稳定性的要求[3]。

因此，采取上述构造措施的情况下，仅需使钢梁满足承载力要求和变形要求，计算公式如下：

将式(2)代入式(6)可得到

式中：Mx为绕X轴的弯矩设计值；γx为截面塑性发展系数；Wx为对X轴的截面模量；f为抗弯强度设计值；[v]为挠度容许值；α与梁、柱线刚度比相关常数。

假设承载力要求和变形要求刚好同时满足，即联立式(5)、(7)，得到梁高跨比为：

将上式h/l定义为钢框架梁的临界高跨比λL[10]。

根据上节结论， 当K=2/3 时，β=1.87，α=1.5。根据经验，钢框架梁跨中弯矩的设计值和标准值的比值Mx/M0取1.35。截面板件宽厚比等级为S4 级时，γx可取1.0。

将上述条件代入式(9)，得到临界高跨比λL为：

临界高跨比是一个与钢材强度、弹性模量和挠度容许值有关的常数。根据GB 50017—2017《钢结构设计标准》[3]要求，钢框架梁挠度容许值可取l/400。Q355B 钢框架梁临界跨高比计算结果约为1/15。

4 变电站推荐高跨比

当钢梁高跨比等于临界高跨比时，承载力要求和变形要求刚好同时满足，此时，截面性能得到充分发挥，截面最优。根据式(6)，本文定义钢梁的临界荷载标准值qL：

当外部荷载大于qL时，需要增加梁高使式(5)和式(6)刚好成立，式(6)受梁高变化影响更为显著，变形要求更易满足，此时梁截面由式(5)承载力要求控制。反之，当外部荷载小于临界荷载qL时，可减少梁高使式(5)和公式(6)刚好成立，此时梁截面由式(6)变形要求控制。

因此，可通过对比变电站实际荷载与临界荷载之间的关系，判断钢梁由承载力要求控制还是由变形要求控制，从而确定推荐高跨比的范围。

以某全户内变电站配电装置楼房间为例， 跨度l为10 m， 钢梁截面为WH650×200×8×16，钢材为Q355B，当K接近2/3 时，计算临界荷载qL=85 kN/m。

根据DL/T 5457—2012《变电站建筑结构设计技术规程》[10]，通常楼面恒载取5 kN/m2，墙板恒载取10 kN/m，楼面活载取4 ～10 kN/m2；不上人屋面恒载取7.5 kN/m2，活载取0.5 kN/m2。以10 m 板跨计算，该梁折算为均布线荷载标准值情况见表2 所列。

表2 某钢梁均布线荷载标准值

对比变电站钢梁实际荷载与临界荷载qL：当采用Q355 钢时，对于荷载较小的不上人屋面梁和边跨梁，钢梁截面由变形要求控制，钢梁的推荐高跨比小于临界高跨比，可取值1/15 ～1/18；对于设备房间中间跨梁，钢梁由承载力要求控制，钢梁的推荐高跨比大于临界高跨比，可取1/13 ～1/15。

5 模型验证

以某110 kV 全户内变电站配电装置楼电容器室中间跨梁为例，采用PKPM 软件对本文理论进行验证，其中：楼面恒荷载取5 kN/m2，活荷载取9 kN/m2，梁跨度为10 m，钢材选用Q355B。建立该配电装置楼物理模型，如图4所示。

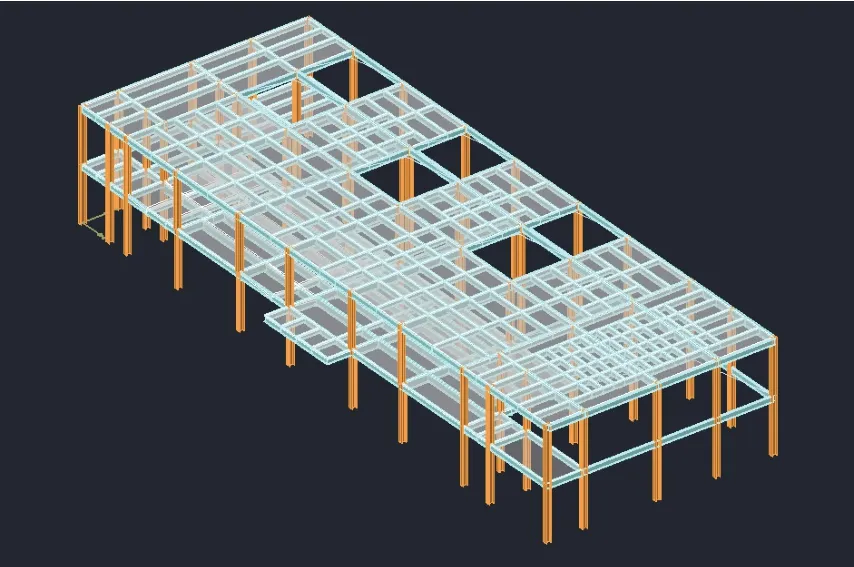
图4 配电装置楼物理模型

分别取不同截面梁试算，梁高在600 ～850 mm 之间、梁宽在200 ～300 mm 之间、应力比在0.9 左右的钢框架梁计算结果见表3 所列。

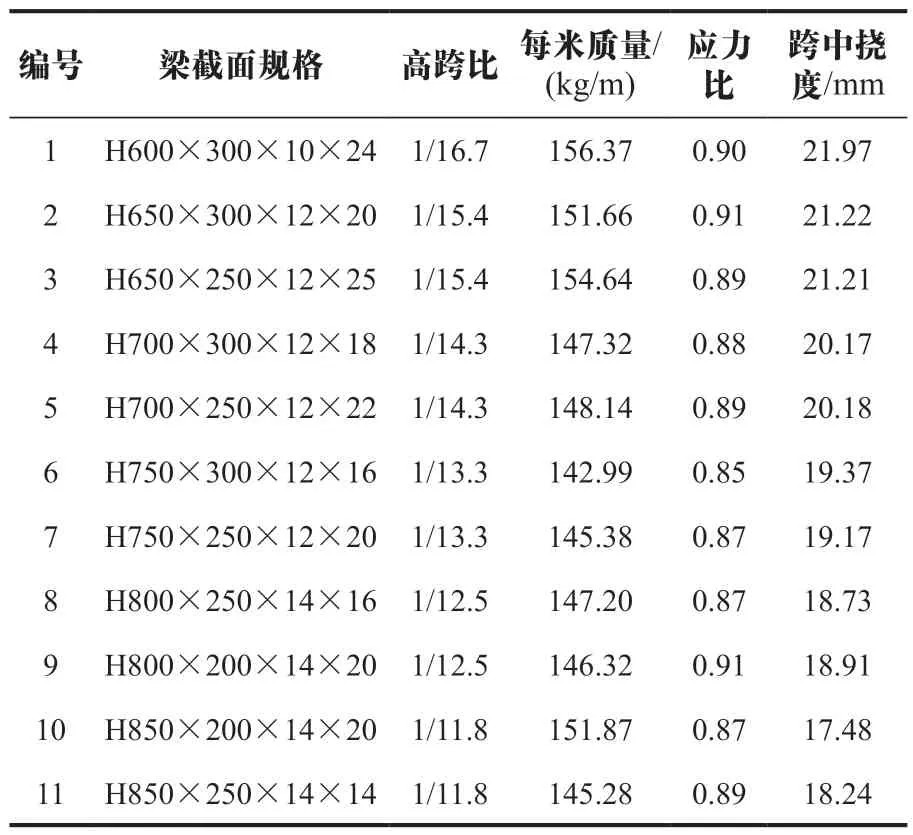
表3 钢框架梁计算结果

由表3 可知，当高跨比在1/12.5 ～1/14.3之间时，钢梁应力比在0.90 左右，挠度满足限值要求，钢梁截面合理，钢材性能得到充分发挥的同时用钢量较少。

综上所述，当采用Q355 钢时，设备房间的梁最优高跨比在1/13 ～1/15 范围内，与理论分析结论一致。

6 结语

本文采用静力分析的方法，通过对钢框架梁柱线刚度比、钢梁临界高跨比的研究，结合变电站钢框架特点和以往工程实践，推导出适合变电站钢框架结构的最优梁柱线刚度比和钢框架梁推荐高跨比，为截面选型和设计提供依据。

本文取得的主要结论如下：

1)增加H 型钢梁高度，能够显著提高钢梁抗弯性能，同时用钢量增加最少；

2)梁柱线刚度比K=2/3 时，跨中弯矩与支座弯矩绝对值相等，钢梁弯矩设计值最小、截面最优；

3)钢框架梁临界高跨比可用于判断设计控制条件，临界跨高比数值与梁柱线刚度比、钢材强度、弹性模量和钢梁挠度容许值有关。当K=2/3时，Q355 钢材钢框架梁临界跨高比为1/15；

4) 当采用Q355B 钢时，变电站配电装置楼设备房间中间跨梁推荐高跨比建议取1/13 ～1/15，不上人屋面及边跨梁推荐高跨比建议取1/15 ～1/18。