分数阶光敏神经元的动力学特性分析及其同步研究

杨宁宁 孟诗悦* 吴朝俊

①(西安理工大学电气工程学院 西安 710048)

②(西安工程大学电子信息学院 西安 710048)

1 引言

神经系统是一个庞大而复杂的网络，是由众多神经元通过突触连接形成的信息网络[1]。神经元作为神经系统的基本结构和功能单位，能够感知和传递刺激，具有连接和整合输入信息和传递信息的功能[2]。当神经元受到刺激时，细胞膜内外的离子浓度会发生突变，从而触发动作电位[3]。这种电生理信号沿轴突传输到突触前端，进一步被相邻神经元的突触后端捕获和感知，实现神经元之间信号的传输和编码。单个神经元在受到相邻神经元或外部刺激后，可诱发多种放电模式，如静息态、周期放电态、混沌放电态等复杂的放电模式。在实际环境中，神经元并不是独立存在的，而是彼此通过突触相互耦合、相互影响的。因此搭建神经元电路为研究其复杂的非线性动力学行为和信息传输提供了有效的途径[4-6]。常见的神经元模型有Hodgkin-Huxley模型[7]、FHN模型[8]、Hindmarsh-Rose模型[9]、Izhikevich[10]模型等。

在实际的生理环境中，神经元会受到如光照、温度、外磁场等外部刺激的影响，此时其输出电压可以反映神经元电路的兴奋性。马军[11]在单个神经电路中嵌入不同的物理器件设计了光敏神经元、热敏神经元等多种功能神经元。Liu等人[12]用光电管来激活FHN神经元模型，详细地分析了系统参数对神经元放电模式的影响。现有的基于理想元件的神经元电路研究主要集中在整数阶，而研究表明分数阶神经元模型更精确，可以提高信息处理的效率。Yao等人[13]分析了分数阶FHN神经元的动力学特性，并证明了分数阶神经元更适合与模拟神经行为。Yang等人[14]研究了忆阻突触耦合分数阶神经元的同步特性。研究结果表明随着分数阶阶次的变化，神经元在周期态和混沌态之间过渡。Abdelaty等人[15]研究表明分数阶模型由于额外的自由度，可以丰富模型的灵活性和动态特性。

本文的其余部分组织如下：在第2节中，提出了分数阶光敏神经元模型；在第3节中，通过分岔图、相轨迹图和时间序列图等方法分析了分数阶光敏神经元的动力学行为；在第4节中，采用dSPACE验证了仿真结果。最后，对全文进行了总结并说明了本文所提出的模型潜在的应用前景。

2 分数阶光敏神经元数学模型

光线进入眼睛，在视网膜上感光并触发神经电活动响应，从物理过程来看视网膜实现了光电转换，把电磁波能量转化为生物电信号，并以动作电位的方式进一步刺激脑视觉功能区来产生响应。光敏神经元模型可以近似模拟这一物理过程，而分数阶光敏神经元比整数阶模型更精确，动力学行为更丰富，此节介绍分数阶光敏神经元模型。

2.1 分数阶光敏神经元

本文在文献[16]整数阶光敏神经元的基础上，用分数阶电容和电感替代整数阶神经元电路中的理想元件，得到了分数阶光敏神经元电路模型，如图1所示。其中 NR 是非线性电阻，C表示分数阶电容，L为分数阶电感，R是与感应线圈串联的电阻，iS代表外部刺激电流，E为施加的恒定电压源，VS为余弦电压源，RS为支路的电阻。

图1 分数阶光敏神经元电路示意图

根据基尔霍夫定律、伏安关系及分数阶电容、电感模型[17,18]得到图1的电路方程为

非线性电阻 NR的电压和电流之间的关系表达式为[16]

其中，ρ,V0是电阻的归一化参数；V是非线性电阻的电压。

对电路方程式(1)采用以下的无量纲变换

从而得到分数阶光敏神经元的动力学方程[19]

其中，x表示膜电位，y表示恢复变量对应的慢电流， 0＜q ≤1 是分数阶的阶数，a,b,c,ξ是系统参数。外部激励源和光电管输出为uS=B1cosωτ，且ug=B2cosωτ。其中B1、B2和ω分别表示激励和光电管的幅值和频率。也就是说，光电管可以用作电压源，产生时变刺激，激活神经回路。

2.2 稳定性分析

从分数阶系统(4)中移除外部电压源和光电管输出，对此神经元进行稳定性分析

假设平衡点为 (x0,y0)，此点的雅可比矩阵为

相应的特征方程为

相应的特征值为

如果其中一个特征值满足

平衡点是不稳定的。显然，它是由参数a,b,c和参数ξ决定的。

3 数值仿真及动力学分析

在本节中，通过数值仿真分析分数阶光敏神经元模型的动力学特性。系统的归一化参数选取为a=0.7，b=0.8，c=0.1，ξ=0.175，变量初始值为(x0,y0)=(0.2,0.1)。

3.1 分数阶阶次q =0.99

取参数B1=0.8，ω=0.4，B2=0.2，绘制系统的动力学随参数B1和ω变化的分岔图，如图2所示。可以看出，改变外界驱动参数B1和ω，可以使系统在周期放电和混沌放电之间过渡。

图2 q=0.99时不同分岔参数下的分岔图

当固定其他参数不变时，随着参数B1的增大，系统由单周期放电过渡到混沌放电状态，而后转变为双周期放电状态(图3)。若只改变参数ω，系统经过单周期放电、尖峰放电过渡到混沌放电，而后转为双周期放电状态(图4)。结果表明，在不同的参数选择下，系统膜电位可以呈现出不同的放电模式，即周期放电态、尖峰放电态及混沌放电态。

图3 q=0.99时参数B1取不同值时的相图及时间序列图

图4 q=0.99时参数ω取不同值时的相图及时间序列图

3.2 分数阶阶次q =0.9

取参数B1=0.8，ω=0.4，B2=0.2，随参数B1和ω变化的分岔图如图5所示。可以看出，随着分数阶阶次的降低，系统的混沌区域减少且时间滞后，神经系统对外界信号的适应能力增强。

图5 q=0.9时不同分岔参数下的分岔图

当固定其他参数不变时，随着参数B1的增大，系统在周期放电状态和混沌放电状态之间转换(图6)。若只改变参数ω，系统经过周期放电过渡到混沌放电，而后转回单周期放电状态(图7)。结果表明，在不同的参数选择下，系统膜电位可以呈现出不同的放电模式，即周期放电态、尖峰放电态及混沌放电态。

图6 q=0.9时参数B1取不同值时的相图及时间序列图

图7 q=0.9时参数ω取不同值时的相图及时间序列图

3.3 随分数阶阶次 q 变化

考虑到分数阶阶次q的变化对分数阶光敏神经元电路动力学特性的影响。取B1=0.8，ω=0.4，B2=0.2，q ∈[0.9,1] 。系统随阶次q变化的分岔图如图8所示。由图可以看出，系统随阶次变化的分岔图可以分为两种状态：周期状态和混沌状态。当q ∈[0.9,0.962] , [0.967,0.97] , [0.973,0.974]时，系统处于周期态，当q ∈[0.962,0.967] , [0.97,0.973],[0.974,1]时，系统会表现出复杂的混沌状态。

图8 系统随阶次q变化的分岔图

3.4 基于电突触耦合策略的分数阶光敏神经元的同步控制

神经元同步在大脑信息交流和处理的过程中发挥了重要的作用。本文采用电突触耦合方式实现了两个分数阶光敏神经元的同步。如果忽略耦合的时间延迟，则两个光敏神经元组成的系统为其中：a,b,c,ξ是参数，r是耦合强度，0＜q ≤1是分数阶的阶数。

设e1=x1-x2，e2=y1-y2，若t →+∞时，有e=|e1|+|e2|→0，则两个耦合神经元达到完全同步。取定系统的归一化参数B1=0.8，ω=0.4，B2=0.2，r=50， 系统初始值为 (x1,y1)=(0.2,0.1),(x2,y2)=(0.02,0.01) ，分数阶阶次q=0.99和0.9，光敏神经元不同阶次对初值的同步如图9所示。

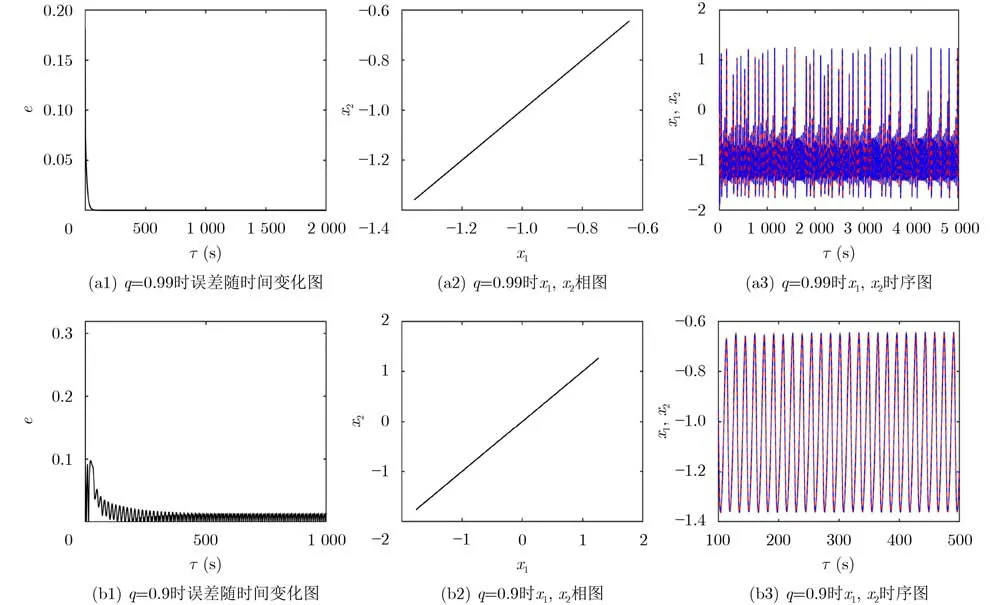
图9 光敏神经元不同阶次对初值的同步

由图9可知，在相同的耦合系数下，当q=0.99时，两个分数阶光敏神经元之间可以达到完全同步；当q=0.9时，两个光敏神经元之间相位同步，尖峰的高度不等，实现了近似同步。

4 基于dSPACE的分数阶光敏神经元实现

本文利用时域-频域转换法，构建分数阶积分器，对模型进行分数阶求解。然后采用dSPACE工作平台(如图10)对Simulink输出信号经比例缩放验证分数阶光敏神经元的动力学行为，其中系统参数变化对动力学特性的影响如图11-图14所示，分数阶光敏神经元的耦合同步如图15所示。

图10 基于dSPACE的工作实验平台

图11 q=0.99时参数B1取不同值时的相图及时间序列图

图12 q=0.9时参数B1取不同值时的相图及时间序列图

图13 q=0.99时参数ω取不同值时的相图及时间序列图

图15 光敏神经元不同阶次对初值的同步

5 结束语

本文在整数阶光敏FHN神经元电路中引入分数阶微积分理论，提出了分数阶光敏神经元模型。通过分岔分析，光电流的改变可以诱发系统丰富的放电模式，如周期放电、尖峰放电和混沌放电状态。综合分析结果表明，分数阶光敏神经元系统对相同的外部信号表现出更多的周期性放电区域，随着分数阶阶次的降低，分数阶系统的混沌区域减少，光敏神经元的活跃度增加，对外界信号的适应能力增强。数值仿真和dSPACE实现结果表明，当选取不同的系统参数时，神经元系统在周期放电和混沌放电状态之间转换；当参数选取不同值时，系统可以诱发周期放电、混沌放电、尖峰放电等不同的放电模式。此外，使用电突触耦合的方式连接两个分数阶光敏神经元，并通过调整耦合系数来实现神经元之间的相位同步和完全同步。结果表明，分数阶神经系统具有较强的信息编码和传输能力，对进一步研究功能性神经电路与神经网络的应用具有一定的借鉴意义。