全双工主动窃听非正交多址接入系统智能超表面辅助物理层安全传输技术
阔永红 曹 琳 吕 璐 贺冰涛 陈 健
(西安电子科技大学通信工程学院 西安 710071)
1 引言
第6代(the Sixth Generation, 6G)通信技术需要支持的用户及设备数量将大量增加,与之伴随而来的是高要求的性能指标、高复杂度的网络、高成本的硬件和日益增加的能源消耗,这些需求需要更智能的技术来解决。智能超表面(Reconfigurable Intelligent Surfaces, RIS)能重新配置无线传播环境,因此受到广泛关注。RIS由许多无源低成本的反射元件组成,每个元件可以独立地调节反射信号的振幅和相移,从而增强或抑制用户处接收的信号[1],提升系统性能[2]。另一方面,非正交多址接入(Non-Orthogonal Multiple Access, NOMA)技术被普遍认为是提高频谱效率和实现大规模连接的有效解决方案[3]。NOMA通过使用叠加编码和串行干扰消除(Successive Interference Cancellation,SIC)技术,可以在同一资源块中同时服务多个用户,促进用户之间的频谱共享,有效提高频谱效率。RIS和NOMA的结合是双赢的选择。NOMA可以提高RIS系统的频谱效率,RIS可以通过调控无线环境来确保用户的组合信道之间产生差异,以更好地实现NOMA[4]。文献[5]中通过联合优化主动和被动波束赋形,利用RIS提高NOMA系统的能量效率。文献[6]利用RIS辅助NOMA系统的反向散射通信,研究了对应场景下的中断概率,并证明了可以通过增加RIS反射元件来提升NOMA网络中的远用户性能。
然而,无线信道的广播性和开放性为信息传输提供便利的同时,也为非法用户窃取信息提供了可乘之机,给无线通信传输带来了潜在的安全隐患。信息保密和隐私保护已成为开发6G无线通信的关键任务,通过物理层安全来保护NOMA通信的相关研究早已展开[7]。物理层安全技术可以有效防止信息泄露,但其主要基于合法接收者和恶意窃听者之间的信号质量差异来实现,因此安全效果依赖于通信的电磁环境。引入可智能调配无线传播环境的RIS,为NOMA系统的物理层安全提供了更广阔的研究空间。文献[8]针对RIS-NOMA系统提出了一种通过人工噪声实现安全通信的策略,在满足系统安全速率需求的前提下最大化合法用户的和速率。文献[9]中则考虑了具有不完美信道状态信息(Channel State Information, CSI)的窃听场景,使用人工噪声确保RIS-NOMA系统的安全传输,实现系统要求的安全速率。
上述关于RIS-NOMA物理层安全的工作都假设窃听者以半双工模式执行被动窃听。但窃听者可能具有更强大的信号处理能力。如果网络中存在同时执行主动干扰和被动窃听的全双工窃听者,会带来更严重的安全隐患。由于NOMA本就存在用户间的同频干扰,窃听者发射的主动干扰可以显著降低用户的数据速率,从而引发传输中断。此时若增大发射功率可以有效避免传输中断,但窃听者处的信噪比也会增大,因此需要在增强或抑制合法信号之间进行权衡。另一方面,多数工作中以可以获取窃听者的全部或部分CSI为前提进行后续研究,但是在实际网络中,窃听者属于不受信任的非法用户,往往不会主动与基站交换CSI,因而合法系统很难获取到窃听者的瞬时CSI。如果合法系统只知道窃听者的统计CSI,会导致RIS无法准确调整信道以防御窃听,且合法系统不能精确判断干扰大小,进而威胁到传输的安全性和稳健性。如何利用RIS来抵抗仅已知统计CSI的全双工窃听者,保护NOMA传输,是亟待解决的关键问题。
基于上述分析,本文研究全双工攻击下的多用户NOMA下行通信系统的物理层安全问题。在仅已知窃听者统计CSI的情况下,提出了全新的RIS辅助鲁棒波束赋形方案,来保障NOMA通信系统的安全性与可靠性。具体地,本文以系统传输中断概率和保密中断概率作度量,联合优化基站发射波束赋形、RIS相移矩阵、传输速率和冗余速率,以最大化系统保密速率。由于所形成的联合波束赋形优化问题为多变量耦合的高度非凸问题,且存在难以处理的概率性约束。为克服这一难题,本文提出一种有效的交替优化算法来获得波束赋形问题的解,其中使用伯恩斯坦型不等式(Bernstein-Type Inequality, BTI)近似处理概率性约束,使用算术几何平均数(Arithmetic-Geometric Mean, AGM)不等式转换非凸的目标函数,并利用罚函数法处理RIS相移的秩一约束。仿真结果表明,相较于传统方案,所提方案可实现较高的保密速率,且增加RIS反射单元数有利于提升系统保密性能。
2 系统模型和优化问题
2.1 系统模型
本文考虑RIS辅助多用户NOMA系统的下行传输系统模型。系统中包含配置M根天线的基站、K个单天线NOMA用户、1个单天线窃听者和具有N个反射单元的RIS。其中单天线窃听者以全双工方式工作,即窃听者同时进行干扰攻击和窃听攻击。RIS可以通过由智能控制器提供的单独的链路与基站通信,以协调传输和交换信息,且基站可以通过控制器实现对反射单元相移和幅度的实时控制。
假设所有信道都是准静态块衰落信道,且经过相邻元件的反射信道相互独立。基站到RIS、第i个合法用户Ui和窃听者的信道矩阵和向量为:HB,I∈CN×M,hB,i ∈CM×1,hB,E∈CM×1。RIS到用户Ui和窃 听者 的 信 道 向 量 为:hI,i ∈CN×1,hI,E∈CN×1。窃听者到RIS和用户Ui的信道向量为:hE,I∈C1×N,hE,i ∈C1×1。由于信道互易性,RIS到窃听者和窃听者到RIS的信道向量满足关系式hI,E=h。基站到RIS的信道为莱斯衰落信道,其他链路皆为瑞利衰落信道。将第n个元素的反射系数表示为βnejαn,其中αn ∈[0, 2π],βn=1,则R I S 的 反 射 系 数 矩 阵 为Θ=diag{ejα1,ejα2,...,ejαn}T∈CN×N。
由于信道的缓慢变化特性,不失一般性,本文假设基站可以准确地获得合法信道CSI[10,11]。然而,合法系统与窃听者之间是非合作关系,窃听者不会主动将自己的相关信息发送给基站,因此基站很难获取窃听者的瞬时CSI。但是可以通过长期监测来估计窃听者信道的统计特性,例如E{|hB,E|2}=L等[7]。则窃听者的信道向量估计值由式(1)给出
其中,LB,E,LI,E,LE,i表示大规模路径损耗因数,ΔhB,E, ΔhI,E, ΔhE,i表示遵循循环对称复高斯分布的小衰落分量,I为单位矩阵。则合法用户Ui和窃听者的接收信号分别表示为
其中,wi ∈CM×1表示用户Ui的预编码矢量,si是用户Ui的NOMA信息,且满足 |si|2=1,|zE|2=PJ是 窃听者发射的干扰信号的功率。ni,nE~CN(0,σ2)表示用户Ui和窃听者处功率为σ2的复加性高斯白噪声。为了描述全双工窃听者处由于自干扰消除不完全而产生的剩余自干扰,本文采用了文献[12]中的环路干扰模型,该模型用系数µ∈[0,1]量化了自干扰的等级,µ=0时表示零自干扰。
根据NOMA解码原理,信道增益强的用户可以对信道增益弱的用户信号进行解码。但是RIS的加入会在发射端和接收端之间增加一条级联信道,可能会对解码顺序造成影响。假设RIS相移矩阵的设计使用户信道增益满足条件:|(hΘHB,I+h)wi|2≥|(hΘHB,I+h)wi+1|2,其中 1≤m ≤K,1≤i ≤K-1 ,即第m个 用户能依次解码第1~(m-1)个用户的信号。基于此,合法用户Ui解码自己信号时的可达速率可以表示为
其中hE=hΘhE,i+hE,i。
窃听者处的可达速率表示为
2.2 优化问题
因为合法用户系统仅已知窃听者的统计CSI,无法根据CSI实时调整传输速率,所以采用定速率Rc进行传输。同时为保证系统传输安全性,采用定冗余速率R0。这种情况下,一旦Rc大于合法用户Ui的可达速率Ri,会引发传输中断。同时,如果R0小于窃听者的可达速率RE,i,会造成严重的信息泄露。
为此,本文通过联合优化主动波束成形、RIS的反射系数以及系统的传输速率Rc和冗余速率R0,最大化系统的保密速率,来实现高效且安全的信息传输,建立优化问题式(5)。具体的,优化目标为最大化系统的保密速率,约束C1为基站总功率PB的约束,约束C2为NOMA用户间的SIC解码顺序约束,约束C3为系统传输中断约束,约束C4为系统保密中断约束,约束C5为RIS相移约束。由于概率约束C3,C4为非凸约束,且变量Θ,wi,Rc,R0存在耦合关系,因此问题式(5)很难求解
3 联合波束赋形算法
3.1 优化问题转换
先将问题式(5)转换为更容易求解的形式。约束C3展开为
由前述分析可知,因为合法用户无法获知窃听者的瞬时CSI,即合法用户无法准确获知式(6)中的|hE|2PJ,因而可能会发生传输中断的现象。假设当|hE|2PJ=Γ时,系统以速率Rc进行传输正好不会中断,则当|hE|2PJ>Γ时,系统以速率Rc传输时会中断。因此C3的概率约束等价于
其中,hE可展开为,根据文献[13]中的论点1,在 [0,2π]范围内服从独立均匀分布,即对于合法用户而言干扰信号的级联链路中的RIS相移是随机相移。根据文献[14]中的论点2,可以得到|hE|~CN(0,N|LE,iLI,i|2+|LE,i|2) ,即|hE|2服从指数分布。可求得式(7)为
则当系统传输正好不发生中断时,传输速率Rc可表示为
最大化Rc,Γ应取最小值,令Γ=PJ(N|LI,ELI,i|2+|LE,i|2)ln(1/pout) 。 将式(9)带入目标函数替换Rc。
接下来对约束C4进行处理,使用BTI来解决统计信道不确定性。本文考虑最坏情况,窃听者可以消除NOMA传输中的同频干扰,则约束C4可以写为
根据文献[15]的论点2,利用BTI并引入辅助变量ϕi,可将式(10)近似为
进一步,令变量hui=hΘHB,I+h,HB,i=huih,Wi=wiw。则约束C2可以写为
经过以上处理,进行整理后,问题式(5)可以写为
问题式(13)中变量Θ,Wi耦合,采用交替优化的方式将问题式(13)拆解为两个子问题进行求解。
3.2 求解基站波束成形 Wi 和冗余速率R0
固定RIS反射系数Θ,问题式(13)可以写为
为解决目标函数中的分式结构,引入满足式(15)的松弛变量zi
通过AGM不等式[16]将式(15)写为
令s=2R0,则目标函数可以重写为
对于式(17)右侧的分式结构,引入满足关系ζ ≤1+zi/s的松弛变量ζ,并通过AGM不等式将ζ ≤1+zi/s重写为
整理后问题式(14)可写为
问题式(19)是凸优化问题,可以用凸规划求解器进行求解。且式(19)求得的解总是满足rank(Wi)=1的,证明如下:
证明问题式(19)是优化变量{Wi,zi,s,ζ,ϕi,Φi}的联合凸函数,并且满足Slater约束条件,即具有强对偶性。用Wi表示的拉格朗日函数由式(20)给出
其中,ξ包括不涉及Wi的所有项。υ,γi,µi,Xi,Yi为拉格朗日乘子,分别满足条件:υ ≥0,γi ≥0,µi ≥0,Xi≽0,Yi≽0。列出问题式(19)的Karush-Kuhn-Tucker(KKT)条件
为了避免对偶问题的可行解空间无界,令υ ≥0 。进而,KKT约束K1应当满足ρmax(Λi)≤υ。如果ρmax(Λi)<υ,则Y i*≻0 ,即是一个正定矩阵,那么=0。因此ρmax(Λi)=υ,即Y i*是一个半正定矩阵,且根据文献[17]的附录A,可以得到关系式M >Rank(Y i*)≥M-1。
引理1西尔维斯特不等式:对于矩阵A ∈CS×U和B ∈CU×W(S, U, W为任意正整数),有如式(23)的不等式成立
rank(AB)≥rank(A)+rank(B)-U(23)根 据 引 理1 以 及 条 件K 2 可 得L ≥rank(Y i*)+rank(Wi*)≥L-1+rank(Wi*),取该不等式最左端和最右端可得到结论 rank(Wi*)≤1。 证毕
3.3 求解RIS相移矩阵Θ
固定主动波束成形Wi和 冗余速率R0,问题式(13)可以写为
首先,令Gi=[diag(h)HB,I;h] ,=[u;1],u=[ejα1,ejα2,...,ejαN]H,且U=u¯u¯H。整理后,问题式(24)可以重写为
同样,引入松弛变量zi对目标函数进行处理,处理方式同式(15)-式(18)。
为了将约束C8转换为凸线性矩阵不等式(Linear Matrix Inequality, LMI)形式,使用奇异值分解将常数矩阵LI,EHB,IWiHLI,E等价表示为si,q和di,q为奇异值分解运算中的辅助矩阵,1≤q≤N。 令Si,q=[diag(si,q),0],Di,q=[diag(di,q),0]T,则约束C8中的耦合项可以表示为
因此,约束C8可写为
接下来,对问题式(25)中的秩一约束进行转换,根据文献[18]可以进行如式(28)的等价转换
式(28)依然是非凸的,采用基于惩罚的方法将该约束移动到目标函数中,令,则问题式(25)可写为
其中ρ >0,为惩罚因子。问题式(29)是一个凸优化问题,可以用凸规划求解工具进行求解。
4 算法性能分析
4.1 算法收敛性分析
在所提算法的第n次迭代中,可得问题式(19)在 给 定Θn-1时 的 最 优 解Win,R0n和=f(,R0n,Θn-1), 以及问题式(29)在给定Win,R0n时的最优解Θn和=f(Win,,Θn),因此可得≤。在第n+1次迭代中,可得问题式(19)的最优解W,以及R=f(Win+1,R,Θn) ,问题式(29)的最优解Θn+1和R=f(W,R,Θn+1)。由于最优解总能使当前求解得到的结果不小于前一次求解得到的结果,可得≤R≤R。因此问题式(13)的优化目标在每次迭代求解中以非递减的趋势变化,目标函数在问题式(18)的可行解合集上是连续的[19],且发射功率有界,问题式(13)的解存在上界,因而所提算法是收敛的。
4.2 算法复杂度分析
由于两个子问题仅涉及L M I 和2 阶锥体(Second-Order Cone, SOC)约束,因此可以通过标准内点方法求解[20]。可以根据最坏情况运行时间进行计算。问题式(19)的近似复杂度为
其中,n1=K(M+N)2+KM2+2K+2,Δw=K(M+N)+KM+6K。问题式(29)的近似复杂度为
其中,n2=K(M+N)2+K(N+1)2+2K+2,ΔU=K(N+1)+K(M+N)+6K。因此,整个交替优化迭代算法的复杂度为:O(lAO(lwlog2(1/ε)ow+lUlog2(1/ε)oU)),lw,lU分别表示求解问题式(19)和式(29)的迭代次数,lAO表示收敛所需的迭代次数。
5 仿真分析
本节对本文提出的交替优化方案的性能进行仿真及结果分析。仿真的网络拓扑为2维坐标系,系统中的基站、RIS、窃听者分别位于处(0,10),(60,10),(50,0),合法用户随机分布在圆心为(70,0),半径为5 m的圆内,用户数K=2。信道模型相关参数设置为:αB,I=2.0,αB,E=αB,i=3.0,αI,E=αI,i=2.2,αE,i=3.2,κ=3; 噪声功率σ2=-100 dBm;窃听者的剩余自干扰系数µ=0.000 1;窃听者发射的干扰信号功率PJ= -20 dBm;中断概率门限和保密概率门限设为pout=pso=0.1。仿真中同时给出3种基准方案的结果进行性能对比。基准方案1为所提算法应用于RIS-OMA系统的对应方案;基准方案2为文献[21]中的基于分解的大偏差不等式算法;基准方案3为RIS随机相移方案。
图1为本文所提交替迭代算法收敛过程的仿真结果。为了说明算法的收敛性,忽略了用于优化发射波束成形和RIS相移矩阵的内部迭代步骤,仅记录外部交替迭代的次数。图1中的3条曲线分别是RIS反射单元数目N固定为10, 20, 30时的收敛曲线。如图1所示,保密速率随迭代次数的增加而单调增加,并且在有限迭代次数内能较快地收敛到稳定点。
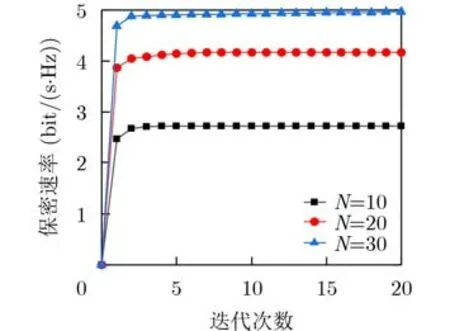
图1 算法收敛图
图2为保密速率和基站发射功率的关系曲线。仿真中,M=4,N=10。从图2可以看出,随着基站发射功率的提高,系统的保密速率不断增加,且本文方案始终优于对比方案。因为,RIS随机相移方案并没有充分发挥RIS改变信道条件的优势,NOMA传输可以在整个传输阶段同时为所有合法用户服务,因此在相同的发射功率下,所提方案能够提供比其他对比方案更高的保密速率。同时,可以观察到,保密速率在低发射功率阶段缓慢增加,而在高发射功率阶段快速变化。主要原因如下:(1)当基站发射功率较低时,来自窃听者的主动干扰和被动窃听都严重威胁合法信号传输,此时,保密中断事件和传输中断事件发生的概率都较大,传输速率和冗余速率受到的约束程度很紧。在满足系统要求的情况下,增大发射功率时,传输速率和冗余速率的增长都比较缓慢,因此两者之差,即保密速率缓慢增加;(2)当发射功率变大时,干扰攻击对信号传输的威胁变小,可以轻松地达到系统传输中断概率需求,对于传输速率的约束程度变松,传输速率的增速变快,因此保密速率可以快速增加。
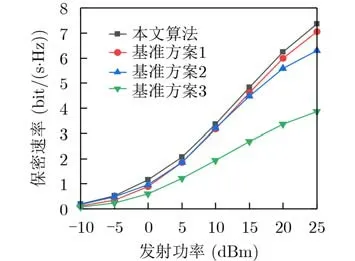
图2 保密速率与基站发射功率的关系
图3为保密速率和RIS反射单元个数N的关系曲线。仿真中,基站发射功率设为10 dBm。从图3可以看出:(1)保密速率随RIS反射单元个数N的增加而单调增加,但保密速率增长的速度却随N的增加逐渐减小;(2)增加至少10个RIS反射单元个数带来的保密速率增益才能基本等同于增加2根发射天线带来的保密速率增益。单位RIS反射单元带来的保密率增益远不如单位发射天线带来的增益。出现以上现象的原因是,增加RIS的反射单元数量虽然可以带来更高的自由度去增强合法信号,但同时也会增加干扰信号,而改变发射天线数仅对合法信号传输造成影响。但相较于基站处的发射天线,RIS具有低成本、低功耗的优势,因此在成本和能耗有限的情况下,需要进行权衡,应合理选择发射天线数和RIS反射单元数以获得期望的系统保密性能。
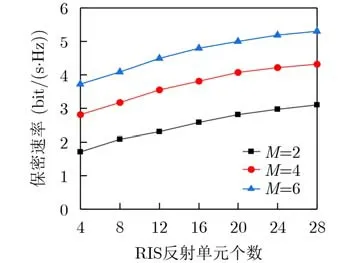
图3 保密速率与RIS反射单元个数N的关系
图4为保密速率和用户群到基站距离的关系曲线。图4中的3条曲线是用户数K为2, 4, 6时的仿真结果。仿真中,基站发射功率设为10 dBm,且基站、RIS和窃听者位置固定不变。从图4中可以看出,当系统中的用户数量增多,系统保密速率减小。值得注意的是,用户群远离基站能获得更高的保密率。原因是窃听者处于基站和用户群之间,当用户群距离基站近的时候,离窃听者也近,收到的干扰较大,严重降低了系统传输速率。随着用户群和基站之间距离的增大,相比较合法信号强度衰减,来自窃听者的干扰强度衰减地更快,因此保密速率不降反升。这得益于RIS可以根据实际情况调整相移矩阵,针对性地减缓合法信号强度的衰减。同时可以看出保密速率增加的速度逐渐变慢,并且到达一定距离后保密速率开始减小。因为RIS是无源的,只能减缓信号强度衰减速度,并不能增强合法信号强度。随着距离的增大,窃听者的干扰攻击带来的负面影响程度一直在减小,逐渐地,合法信号的衰减对传输速率的影响占领了主导地位。
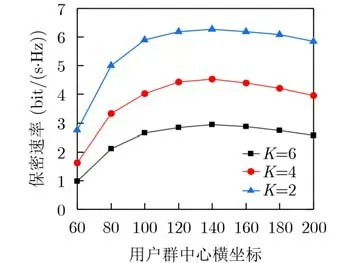
图4 保密速率与用户群位置的关系
6 结论
本文对全双工攻击下的多用户NOMA系统的物理层安全通信进行研究,提出一种RIS辅助的鲁棒波束赋形方案。考虑到系统中存在同时进行窃听和干扰攻击的全双工窃听者,且合法系统仅可获得窃听者统计CSI,本文以系统传输中断概率和保密中断概率作为度量,建立了发射波束赋形矢量、RIS相移矩阵、传输速率和冗余速率的联合优化问题,以最大化系统的保密速率,并提出一种有效的交替优化算法将原多变量耦合非凸问题转化为凸问题,并求得次优解。仿真结果表明,所提方案可实现较高的保密速率,RIS能有效抵抗仅有统计CSI的全双工窃听者。

