基于多维扩展的正交时序复用波形框架及其性能分析

王震铎 谭正锋 孙溶辰

(哈尔滨工程大学信息与通信工程学院 哈尔滨 150001)

1 引言

B5G和6G无线通信系统未来有望提供各种高精度传感服务，如机器人导航的室内定位、智能家居的Wi-Fi传感和自动驾驶汽车的雷达传感[1]。新一代物理层波形被要求具有高可靠、低延迟、适应高多普勒频移环境的能力。正交时频空(Orthogonal Time Frequency Space, OTFS)调制能够有效地对抗时变信道中的多普勒效应，在解决高迁移率问题方面显示出巨大的潜力[2-10]。然而，OTFS需要使用辛快速傅里叶变换(Symplectic Finite Fourier Transform, SFFT)进行调制，这极大地增加了OTFS调制的计算复杂度。最近提出的正交时序复用(Orthogonal Time Sequency Multiplexing,OTSM)调制在时延-序列域中复用信息符号，使得在时域中表现出快时变特性的高速移动信道在时延-序列域中表现出了时不变特性，从而获得与OTFS类似的性能[11]。但由于沃尔什-哈达玛变换(Walsh-Hadamard Transform, WHT)只需要进行加减法运算，OTSM调制复杂度比OTFS低。目前的研究表明，OTSM在部分均衡中展现出了优异的性能，如最大比合并(Maximum Ratio Combining,MRC)迭代均衡[12]、高斯-赛德尔(Gauss-Seidel,GS)迭代均衡[11,13]。有鉴于此，OTSM具有更强的研究潜力。

基于加权类分数傅里叶变换(Weighted(-type)FRactional Fourier Transform, WFRFT)的混合载波(Hybrid Carrier, HC)设计理念由于其集成了传统单载波(Single Carrier, SC)和多载波(Multi-Carrier, MC)波形，具有较强的灵活性和复杂环境的适应能力，从而得到了广泛的关注[14-19]。近些年来，该类一体化波形框架的研究包括了基于WFRFT的HC-Alamouti变电站通信系统[15]、基于WFRFT的无循环前缀的HC系统[16]、双参数可调的WFRFTOTFS系统[17]、基于离散分数傅里叶变换-OFDM系统上的OTFS系统[18]和基于快速卷积的HC系统[19]等。目前来看，基于WFRFT的HC波形系统的研究较为完善，在面对部分应用场景时具有足够的适应能力。但该类HC波形仅使用了WFRFT，波形扩展的维度较为单一，难以表征为使用了其他变换的MC波形，特别是使用了WHT的OTSM，因此该类HC波形的灵活性有所欠缺。考虑到B5G和6G无线通信系统的高标准要求，研究其他维度的HC方案势在必行。

考虑到在高速移动信道环境中OTSM具有和OTFS类似的性能，本文设想存在一种以OTSM为起点的波形方案，这类方案能够退化为传统的SC波形。然而，文献[17]中的WFRFT只能使OTFS波形与SC波形融合，不能使OTSM波形与SC波形统一。为了使OTSM波形能够与SC波形融合，本文根据WFRFT的原理设计了加权分数沃尔什-哈达玛变换(Weighted(-type) FRactional Walsh-Hadamard Transform, WFRWHT)。考虑到WFRFT能够连接S C 和O T F S 的特点，本文以W F R F T 和WFRWHT为基础，设计了以OTSM波形为起点，融合OTFS, SC, HC等波形的WFRFT-WFRWHTOTSM 2维参数可调的一体化波形框架。在本实验中使用的均衡为GS迭代均衡，信道模型为扩展车辆信道模型(Extended Vehicular A model, EVA)。仿真结果表明，在不同的高速移动信道环境中，本框架可以通过改变2维阶次以适应相应的环境，得到更好的误码率(Bit Error Ratio, BER)及峰均功率比(Peak-to-Average Power Ratio, PAPR)性能。

2 WFRFT和WFRWHT的定义与性质

2.1 WFRFT

从定义上看，WFRFT是对同一个信号的时域表达式和频域表达式进行加权求和。阶数为α的4项加权N维WFRFT矩阵可以表示为

其中，IN为N维单位阵，FN为N维离散傅里叶变换(Discrete Fourier Transform, DFT)矩阵。式(1)中加权系数ωl(α)可表示为

当α=0时，WFRFT矩阵变成单位矩阵，当α=1时，WFRFT矩阵变成DFT矩阵。

WFRFT可被看作连接信号的时域形式和频域形式的曲线，因此在HC系统中应用时成为连接传统SC波形和OFDM系统的桥梁，这为基于WFRFT的新型多载波的波形扩展提供了理论支撑。

2.2 WFRWHT

根据WFRFT在传统通信领域的物理意义，本文试图构建一种全新的变换方法，以实现SC波形和OTSM波形的融合。与WFRFT类似，本文对同一个信号的时域表达式与序列域表达式的加权求和，且不同加权参量的系数同WFRFT相似，定义β阶N维WFRWHT表达式为

其中WN是归一化的N维Walsh-Hadamard矩阵，加权系数ωl(β)可以表示为

当β=0时，WFRWHT矩阵退化为单位阵，当β=1时，WFRWHT矩阵退化为Walsh-Hadamard矩阵。与WFRFT类似，WFRWHT具有阶数连续性(β ∈[-1,1] )、边界性(W0,N=IN,W1,N=WN)、旋转相加性(Wβ+γ,N=Wβ,NWγ,N=Wγ,N Wβ,N)和对称性(WTβ,N=Wβ,N)。

与WFRFT类似，WFRWHT可被视作连接信号的时域和分数域的曲线。因此，WFRWHT作为一种预编码可以对OTSM进行扩展，实现OTSM波形和SC波形的统一。

3 基于WFRFT和WFRWHT多维扩展的OTSM系统框架

将WFRFT作为一种预编码可以实现OTSM的波形扩展，但这种扩展只能将无预编码的OTSM波形与基于DFT预编码的OTSM波形连接，无法实现SC波形与OTSM波形的统一。本文提出一种基于WFRWHT的新型波形扩展方法，用于融合SC与OTSM波形。进一步地，若将WFRFT和WFRWHT作为预编码方法加在OTSM波形前，即对OTSM波形进行2维扩展，就能得到WFRFT-WFRWHTOTSM波形框架，实现OTSM, OTFS, SC和HC波形的统一，具体系统框架如图1所示。

图1 WFRFT-WFRWHT-OTSM系统框架

基于WFRFT和WFRWHT的多维扩展的一体化OTSM框架可通过对2维参数α和β的灵活配置，表征为不同的波形模态，得到更广泛的适用性和更强的适配能力，能够适应不同的应用需求和性能需求。WFRFT-WFRWHT-OTSM的参数与表征波形关系如表1所示。具体WFRFT-WFRWHT-OTSM波形融合机理如图2所示。

表1 WFRFT-WFRWHT-OTSM的参数与表征波形关系

图2 WFRFT-WFRWHT-OTSM波形融合机理

3.1 发送端

设x,y ∈CNM×1分别表示系统发送和接收的信息符号，WFRFT-WFRWHT-OTSM的每一帧信号的持续时间和带宽分别为Tf=NT和B=MΔf，其中 Δf= 1/T。在发送端，信息符号x被均匀分割为M个信息向量xm ∈CN×1， 即x=[,,...,x-1]T。最后lmax个xm符号为零填充(Zero Padding, ZP)，这能避免块间干扰。可将向量xm重新排列成发送端的信息矩阵X= [x0,x1,...,xM-1]T∈CM×N。对信息矩阵X沿行进行N点 -α阶WFRFT和N点β-1阶WFRWHT，再沿列进行向量化，即可得到发射信号向量sα,β

所得的发射信号向量sα,β是离散的，但实际上在信道中传输的是连续信号sα,β(t) 。对信号sn,α,β的每一列进行DFT运算，最后通过Heisenberg变换即可得到连续时域信号sα,β(t)。

3.2 时延-多普勒信道

考虑一个具有P个传播路径的基带等效信道模型，其中hi,τi和υi分别是第i路径的路径增益、时延和多普勒频移。令τmax和υmax分别代表最大时延扩展和最大多普勒频移，则信道时延扩展长度和多普勒扩展长度分别为τmaxMΔf和υmaxNT。由于P为有限值，故时延-多普勒域的信道脉冲响应h(τ,υ)具有其离散的表现形式

通过SFFT即可得到时延-时间域的连续时变信道冲激响应h(τ,t)

离散时间基带模型是通过在t=q/MΔf处进行采样得到的，其中0≤q ≤NM-1。 设L={0,1,...,lmax}是离散延迟抽头集，它表示采样周期为 1/MΔf的整数倍的延迟移位。通过接收端的采样，时延-时间域的连续时变信道冲激响应h(τ,υ)变成了时延-时间域的离散时变信道冲激响应h[l,q]

将式(7)代入式(8)，得到时延-时间域的离散时变信道h[l,q]为

其中 sinc(t)=sin(πt)/(πt)，κi表示归一化多普勒频移，ℓi表示归一化延迟移位。κi和ℓi具有如式(10)的关系

假设信道延迟可以近似为 1/MΔf的整数倍，则可将式(10)代入式(9)，得到简化后的时延-时间域离散时变信道h[l,q]

3.3 接收端

在接收端收到的时域信号rα,β(t)表示发送端发射的连续信号sα,β(t) 经过信道h[l,q]并受高斯白噪声的影响，即

其中n(t) 表 示方差为σ2的连续的高斯白噪声。

时域信号rα,β(t)进行Wigner变换，再分成N段，对每段进行IDFT即可得到离散的时域信号rα,β=[α,β,α,β,...,-1,α,β]T∈CNM×1。另一种接收方式则是在接收端对收到的时域信号rα,β(t)在t=q/MΔf处进行采样，就可以直接得到离散的时域信号rα,β。无论如何，离散的时域信号rα,β都 可以看作对连续的时域信号rα,β(t)在t=q/MΔf处的采样集，即

将采样点q划分为N组数据，每组数据M个，即可表示为

此时n=[,,...,n]T。由于ZP的存在，每个rn,α,β仅与sn,α,β和信道噪声nn有关，故

令sn,α,β经过的时域信道矩阵为Hn ∈CM×M，则有

由式(15)、式(16)可得rn与sn之间的关系的矩阵表达式

设矩阵H ∈CNM×NM为时域信道矩阵，则有

从接收端收到的时域信号r与发射端处的时域信号s之间的关系表示为

其中n ∈CNM×1表示方差为σ2的高斯白噪声。

时域信号r沿列向重新排列成信息矩阵,β=[r0,α,β,r1,α,β,...,rN-1,α,β] 。对信息矩阵进行N点1-β阶WFRWHT和N点α阶WFRFT，即可得到接收信息矩阵Y

对式(20)沿行进行列向量化，就能得到接收信号y

将式(22)进行化简，可以得到输入信号x与输出信号y之间的关系为

由式(5)、式(21)、式(23)-式(25)可以看出，当α=0,β=0时，该一体化波形框架的输入端、输出端、输入输出关系退化为OTSM波形，具体公式与文献[9]所提的OTSM框架完全一致；当α=1,β=0时，该一体化波形框架的输入端、输出端、输入输出关系退化为OTFS波形，具体公式与文献[19]所提的OTFS框架完全一致；当α=0,β=1时，该一体化波形框架的输入端、输出端、输入输出关系退化为SC波形。可见，该框架可完全退化为OTSM, OTFS, SC等波形。

4 GS迭代均衡

GS迭代均衡算法由Tharaj Thaj等人提出，它可以作为其他均衡的后续迭代均衡，以得到更高的精度[21]。

GS迭代算法是基于最小二乘估计进行求解的，其核心方程为

其 中，zn=Rnsn+n,Rn=H·Hn,n¯n=·nn。可以得到GS迭代均衡中每次迭代求sn的计算方程为

其中bn和Tn的表达式为

其中，Dn和Ln分别为Rn的对角元素矩阵和下三角元素的矩阵。式(27)中第i次迭代的信息符号可计算为

其中，δ是用于提高64QAM以上的高阶调制方案检测器收敛性的松弛参数。对于4QAM,16QAM等低阶调制，GS均衡的收敛性高，故δ设置为1以提高迭代收敛速度；对于64QAM以上的高阶调制方案，δ过高会导致无法收敛。g为第i次迭代的矩阵的列向元素组成的向量，其表达式为

其中，D(·) 表示硬判决，为信息迭代矩阵。由如式(32)公式得到

5 性能仿真与分析

本节研究了WFRFT-WFRWHT-OTSM框架在不同参数情况下的性能。仿真中所设置的子载波数M=64 ，每个符号数为N=64，调制方式为4QAM和16QAM，载波频率为 4×109Hz，子载波间隔为15 kHz，信道类型为EVA模型，每条径的延迟为[0 30 150 310 370 710 1 090 1 730 2 510] ns，对应功率衰减为[0 -1.5 -1.4 -3.6 -0.6 -9.1 -7.0-12.0 -16.9] dB。接收端采用GS迭代均衡方法，松弛参数设置为1，仿真过程中没有使用信道编码。

图3为OTSM波形在接收端移动速度为120 km/h时不同迭代次数对应的误码率性能。在该图中可以看出，当迭代次数为8次时，GS迭代均衡的性能趋于稳定。因此，为了在得到最优的BER性能的情况下减小计算复杂度，本文将GS迭代均衡的迭代次数设置为10次。

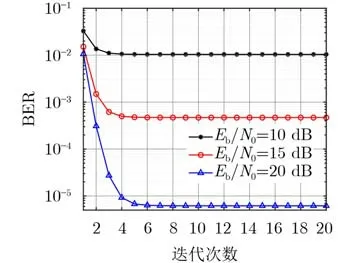
图3 OTSM波形在不同迭代次数时对应的误码率性能

图4比较了α=0时WFRFT-WFRWHT-OTSM波形在120 km/h及500 km/h速度下的误码率性能。当α=0时，WFRFT-WFRWHT-OTSM波形退化成了WFRWHT-OTSM波形。仿真结果表明，对于调制方式为4QAM的情况下，在β=0.1，用户的移动速度为120 km/h且误码率为10-5时，相比于OTSM, WFRFT-OTSM性能增益为1 dB；在β=0.1，用户的移动速度为500 km/h且误码率为10-5时，相比于OTSM, WFRFT-OTSM性能增益为0.5 dB。而对于调制方式为16QAM，用户移动速度为120 km/h和500 km/h的情况下，在β=0.1，误码率为 2×10-6时，相比于OTSM, WFRWHTOTSM的性能增益大于1 dB。

图4 WFRWHT-OTSM波形在时延-多普勒信道下的误码率性能

图5比较了β=0时WFRFT-WFRWHT-OTSM波形在120 km/h及500 km/h速度下的误码率性能。当β=0时，WFRFT-WFRWHT-OTSM波形退化成了WFRFT预编码的OTSM波形。仿真结果表明，对于调制方式为4QAM的情况下，在α=0.1，用户的移动速度为120 km/h且误码率为10-5时，相比于OTSM, WFRWHT-OTSM性能增益为1 dB；在α=0.1，用户的移动速度为500 km/h且误码率为10-5时，相比于OTSM, WFRWHT-OTSM性能增益为0.7 dB。而对于调制方式为16QAM，用户移动速度为120 km/h和500 km/h的情况下，在β=0.1 ，误码率为 2×10-6时，相比于OTSM,WFRFT-OTSM的性能增益大于1 dB。

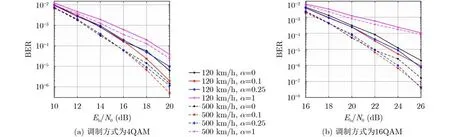
图5 WFRFT-OTSM波形在时延-多普勒信道下的误码率性能

图6给出了速度为500 km/h，调制方式为4QAM，信噪比Eb/N0= 15 dB时，WFRFT-WFRWHTOTSM波形在不同WFRFT、WFRWHT阶次下的误码率性能。图6可以看出，BER分布呈现马鞍形，在OTSM波形，OTFS波形附近，BER性能更好；在SC波形和DFT-OTSM附近，BER性能较差。

图6 WFRFT-WFRWHT-OTSM在时延-多普勒信道下的误码率性能

图7比较了WFRFT-WFRWHT-OTSM波形在速度为120 km/h及500 km/h时的误码率性能。仿真结果表明，在调制方式为4QAM和16QAM的情况下，相比于传统的OTSM波形，基于WFRFT和WFRWHT多维扩展的OTSM波形在高速移动信道中表现出更优的误码率性能，且2维参数具有较强的可选择性，可根据场景、需求的改变进行灵活调整。

图7 WFRFT-WFRWHT-OTSM波形的误码率曲线

如图8所示，给出了过采样倍数为10倍时不同参数条件下一体化WFRFT-WFRWHT-OTSM波形的PAPR性能，并与具有相同总子符号数的OFDM波形进行了比较。该一体化波形的PAPR均优于OFDM波形的PAPR，同时在该一体化波形框架表征为OTSM和OTFS时PAPR性能较差，表征为DFT-OTSM时稍好，表征为SC时较好。当改变α和β时，如果波形越近似于OTFS和OTSM, PAPR性能越差；波形越近似于DFT-OTSM和SC, PAPR性能越好。可以看出，对WFRFT-WFRWHTOTSM的2维参数进行调节可实现对PAPR性能的灵活调控，以适应不同场景以及不同的性能需求。

图8 WFRFT-WFRWHT-OTSM的PAPR性能

6 结论

本文基于WFRFT提出了WFRWHT，实现了传统WHT的广义化，并基于WFRFT和WFRWHT提出了多维扩展的一体化OTSM波形框架，具有2维参数可调的特征。通过对WFRFT和WFRWHT阶次的灵活配置，该框架可退化为OTFS, OTSM,HC, SC等波形，具有灵活可调的BER和PAPR性能，可有效适配多样化的场景和性能需求。仿真结果表明，当接收端采用GS迭代均衡时，WFRFTWFRWHT-OTSM一体化波形在高速移动场景下比OTFS、OTSM波形具有更优的BER和PAPR性能。