可重构智能反射面辅助太赫兹通信系统鲁棒波束赋形算法

袁一铭 徐勇军*② 周继华③

①(重庆邮电大学通信与信息工程学院 重庆 400065)

②(浙江省信息处理与通信网络重点实验室 杭州 310058)

③(航天新通科技有限公司 重庆 401332)

1 引言

随着无线通信系统中数据呈指数级增长，频谱资源变得非常紧张。为此，太赫兹作为6G潜在技术被提出，有望解决当前无线系统中频谱稀缺和容量受限的问题[1]。然而，太赫兹通信受到严重的传播损耗和分子吸收的影响，这极大地限制了其传输距离及通信容量。此外，传播环境中障碍物可能会直接阻断通信。因此，如何能够降低环境对太赫兹波段的损耗成为一个亟待解决的问题。迫切需要从一个新的维度来解决该问题。

可重构智能反射面(Reconfigurable Intelligent Surface, RIS)是一种6G的候选技术，被认为是一种可以重构无线信道环境的新通信范式[2]。该技术以低功耗、提供直射路径的方式解决绕障通信问题。由RIS技术白皮书可知，RIS是一个由许多低功耗、被动、可重构的反射元件组成的均匀阵列平面，通过独立调整反射元件可以改变接收信号的反射路径，有效提高无线网络的容量和覆盖性能[3]。为此，RIS辅助通信技术近年来得到迅速发展。

文献[4]提出了一种发射时间、发射功率和RIS相移联合优化算法，解决无线供电的通信网络场景下吞吐量最大化问题。进一步，文献[5]将上述场景拓展到多天线系统。与上述单一吞吐量优化问题不同，为了以最小的能量消耗获得较高的传输速率(即能耗优化)，文献[6]研究了面向窃听用户的RIS辅助多输入单输出(Multiple Input Single Output, MISO)网络能效最大化问题，利用广义分式规划理论、交替优化理论设计了一种系统总能效最大化波束赋形算法，结果表明了该算法能够克服信道不确定性和用户信息泄露的影响。另外，针对地面基站易受复杂通信环境影响而无法提供视距(Line of Sight, LoS)链路情景，文献[7]研究了基于RIS辅助无人机(Unmanned Aerial Vehicles, UAV)供能通信吞吐量最大算法。但上述大多数工作都没有考虑太赫兹通信问题，文献[8]研究了多RIS辅助太赫兹协作通信系统吞吐量最大化问题，采用深度强化学习算法获得波束赋形向量的解。与上述多跳场景不同，文献[9]研究了多RIS辅助太赫兹单跳通信系统加权和速率最大化问题，考虑用户间干扰，提出了基于空间正交的干扰消除与波束赋形算法。与上述完美信道状态信息(Channel State Information,CSI)不同，文献[10-13]研究了更为实际的鲁棒波束赋形问题(即考虑不完美CSI)。例如，文献[10]将UAV引入到RIS辅助的太赫兹通信系统中，并提出了克服用户窃听的能效最大化资源分配算法。文献[11]研究了RIS辅助太赫兹多输入多输出正交频分多址网络的加权和速率最大化问题，利用交替优化和S-程序设计了鲁棒波束赋形算法。同时，文献[12]采用能量收集模型，研究了RIS辅助无线携能通信太赫兹通信系统中的能耗最小问题。文献[13]考虑了窃听链路不完美CSI，研究了安全和速率最大化的鲁棒多RIS波束赋形问题。现有工作[4-9]从不同的网络模型与优化目标对RIS辅助太赫兹通信系统的波束赋形进行了研究，但大多数工作都是假设系统能够获得完美的信道状态信息。由于低功耗、被动传输的RIS处理能力有限，且太赫兹通信系统存在量化误差与信道时延的影响，从而使得上述工作的假设过于理想，即该系统必然存在信道估计误差导致传输性能不能满足预期设计要求。因此，本文针对该问题提前将信道不确定性考虑到波束赋形算法设计中，从而确保系统的传输稳健性。

虽然现有少量工作[13]研究了RIS辅助太赫兹通信系统的波束赋形问题，但部分CSI已知、连续相移的假设在某些场景中过于理想1当通信系统CSI受到恶劣电磁环境影响或RIS/收发机硬件处理能力受限时，通信网络所有的信道链路都可能存在不确定性，仅假设部分CSI不确定性算法在实际系统中将失效。。此外，由于RIS控制器中A/D转换器精度或信号采样模块能力受限等客观因素的影响，RIS通常情况下是无法提供连续相移调控的，从而使得基于离散相移调控的波束赋形算法在实际系统中失效。

针对上述问题，考虑所有链路CSI估计误差与离散相移的影响2离散相移使得原连续变量耦合问题变为离散变量优化问题，这增加了RIS被动波束的求解难度；此外，所有链路CSI误差会使得所有与信道参数相关的约束条件和目标函数都存在不确定性，这是与传统部分CSI信息已知、总功率最小化问题最大的挑战之处。，本文提出一种基于能效最大的鲁棒波束赋形算法，从而以较低能量消耗来维持一定的传输速率和保证系统的传输鲁棒性。具体贡献如下：

(1)基于基站最大发射功率约束、信道不确定性约束、用户最小速率约束和RIS离散相移约束，建立一个RIS辅助的多用户太赫兹系统能耗最小化波束赋形问题，该问题是一个含参数摄动的非线性、非凸优化问题，难以获得解析解；

(2)利用丁克尔巴赫方法将目标函数解耦转换为两项相减的形式，然后利用S-程序将信道不确定约束转换为确定性约束，最后利用基于连续凸近似和半正定松弛的块坐标下降(Block Coordinate Descent, BCD)和相位映射将原问题转化为凸优化问题，利用凸优化进行求解。

(3)仿真结果表明，相比非鲁棒波束赋形算法，本文鲁棒波束赋形算法能量效率提高15.4%，并能减轻信道不确定性影响，用户中断概率降低15.48%。

2 系统模型

考虑一个RIS辅助下行多用户MISO太赫兹通信系统如图1所示。在该通信系统中，1个含M根天线太赫兹蜂窝基站通过RIS辅助服务K个单天线用户，1个含有N个反射阵元的RIS反射来自太赫兹基站的信号从而增强K个用户的接收信号，并解决LoS被障碍物阻挡的问题。分别定义用户集合K={1,2,...,K} (∀k ∈K)， RIS阵元集合N={1,2,...,N}(∀n ∈N)。

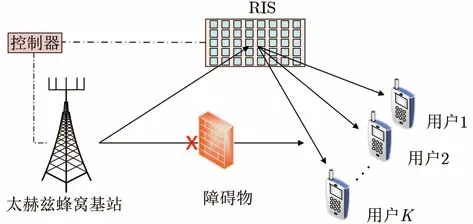
图1 RIS辅助的多用户太赫兹通信系统

不同于较低频段通信，在太赫兹频段的信号更容易受分子吸收如水蒸气和氧气的影响，将导致严重的路径损耗。因此太赫兹基站到RIS的信道模型可以表示为

其中，αr(φr)和αt(φt)分别为接收端和发送端的导向矢量，,i ∈[r,t] ， r 和 t分别表示接收端和发送端，φr和φt分别表示到达角和离开角，d0表示天线间距，ϕi ∈[-π/2,π/2],i ∈[r,t]。

同理，RIS到用户k的信道模型可以表示为=q(f,dk)gk，dk表示用户k到RIS中心点的距离。gk ∈CN×1表示RIS到第k个用户的信道向量，其表达式为

根据图1的信号传输模型，结合式(1)-式(5)，用户k的接收信号可以表示为

其中，Gt和Gr分别为发送端和接收端的天线增益，η为路径损耗补偿因子，其级联路径损耗需满足χ为RIS的阵元增益，Θ=diag(θ)为RIS的相移矩阵，θ=[a1ejϑ1,...,aNejϑN]H，an和ϑn分别表示无源RIS的第n个阵元的幅度和相位反射系数，an ∈[0,1]，通 常 情 况 下 取an=1[14],ϑn ∈ΦL,ΦL={ω,2ω,...,Lω},ω=2π/L,vk ∈CM×1为基站对用户k的波束赋形向量，sj～CN(0,1)为太赫兹基站发送给用户j(∀j ∈K) 的符号，nk为接收机处的背景高斯噪声并服从均值为0、方差为的复高斯随机分布，即nk～CN(0,)。

根据式(6)，第k个用户的信干噪比(Signal to Interference plus Noise Ratio, SINR)可表示为

综合考虑太赫兹基站主动波束赋形功耗和电路功耗，系统的总能量消耗为

其中，PBS,PRIS和PUE分别为在太赫兹基站、单个RIS阵元和用户设备的电路功率消耗。

为了提高系统容量，并且减少功率开销，同时考虑RIS有限硬件调控能力这一事实，基于离散相移的能效最大化波束赋形问题可以描述为

其中， C1 表示基站的最大发射功率约束，Pmax是基站的最大传输功率门限； C2表示RIS的离散相移约束，离散相移比特数为 Bit=log2L； C3表示用户的最小传输速率约束，R表示最小传输速率门限。问题式(9)显然是一个不含有信道不确定性的非鲁棒波束赋形问题。

然而，在实际RIS辅助的太赫兹通信系统中，由于RIS是一个低功耗、计算能力有限的被动传输器件，信道估计不可能非常精准，因此基站与RIS之间的信道增益在实际系统中存在不确定性。另外，由于用户的移动性导致RIS与用户之间的传输链路会因信道时延、量化误差、信道随机性等因素的影响，其信道增益同样是不可能完美已知的。因此，为了保证系统传输的可靠性、降低通信中断，需要考虑问题式(9)中相关信道的不确定性，设计对应的鲁棒波束赋形算法是非常重要的。因此，本文考虑信道和的不确定性，结合问题式(9)设计鲁棒波束赋形算法。具体过程如下：

从基站经过RIS反射到达第k个用户的信道可以重新表示为

其中，Gk ∈CN×M。根据有界信道不确定性，不确定性集合可以表示为

3 波束赋形算法设计

3.1 目标函数转换

根据丁克尔巴赫方法[18]，问题式(13)中分数形式的目标函数可以转化为相减的形式求解，其充要条件为

其中，Ω为问题式(13)的解空间集合。此时，问题式(14)仍难以求解，因为无法提前获得µ*的取值，为了求解该问题，构造函数f(µ)

f(µ)是 一个关于µ的递减凸函数[18]，当式(14)满足时，µ*可以表示为

因此，目标函数可以转换为

3.2 不确定性约束条件转换

其中，式(18)是非凸的。根据泰勒级数展开，式(18)可以线性表示为

然而，式(19)和式(20)属于半无限约束。定义Vk=vk，需满足Vk≽0 和 Rank(Vk)=1。使用以下定理将式(19)和式(20)转化为有限个线性矩阵不等式的等效形式。

定理1(S-程序[17]) 定义fi(x)≜xHAix+2Re{bx}+ci,i=1,2 ，其中Ai ∈CN×N是一个厄密特矩阵，bi ∈CN×1,x ∈CN×1,ci ∈R。f1(x)≤0⇒f2(x)≤0 成立当且仅当存在λ≥0使

式(19)可以展开为

根据等式aHBa=Tr(BaaH)，式(24)可以转化为

根 据 等 式Tr(AHBCD)=vec(A)H(DT⊗B)·vec(C) ，其中⊗表示克罗内克积， vec(·)表示向量化。式(25)可以转换为

令Ak=¯η2(VkT⊗θθH)，根据式(11)、式(26)，可以得到

使用定理1，根据式(27)和式(28)，式(19)可以转化为线性矩阵不等式的形式

类似地，式(20)可以转化为

因 此，定 义Ξ{αk,βk,rk,,λ1,λ2} 和=θθH，问题式(22)可以转化为

由于优化变量Vk和耦合，问题式(31)仍难以求解[16]。基于BCD准则，固定其中一个变量，交替对变量Vk,进行优化，从而求解问题式(31)。此外， C6 和 C7为秩一约束，当解满足秩一约束时，可以通过特征值分解Vk或矩阵获得对应的波束赋形向量。

3.3 优化发送预编码矩阵Vk

通过固定矩阵Θˆ，问题式(31)可以简化为

由于存在秩一约束 C6，问题式(32)非凸，难以求解。因此，考虑半正定松弛方法，将 C6松弛后，用凸优化工具箱(ConVeX optimization toolbox, CVX)工具箱[19]求解。当松弛原问题后，只有满足秩一约束才能将通过特征值分解转化为可行解。否则，需要利用高斯随机化[20]获得问题式(32)的近似解。

3.4 优化相移矩阵

本节给定发送预编码矩阵Vk，根据问题式(31)则有如式(33)的相移矩阵优化子问题

由于约束 C2中的相位离散，式(33)是一个非凸优化问题。根据文献[21]将离散相位ϑn松弛到连续相位ϑn ∈[0,2π) ， C7 与 C6同理，问题式(33)可以转换为

问题式(34)是一个凸优化问题，可以用CVX工具箱求解得到，通过高斯随机化求得连续相移的解为。再根据式(35)将连续相位按ΦL中元素最近距离离散化，从而得到问题式(33)的解Θˆ*。因此设计基于BCD的鲁棒波束赋形算法如算法1所示

3.5 收敛性分析

根据图2，所提算法分包含内外两层，求解Vk和为内层循环，获得 (,)后，在外层求解相应的µ*。由于内层循环是一个标准凸优化问题，最优目标值每次迭代不减[16,17]。另外，Vk由最大发射功率约束Pmax限制而有界，同样Θ˜受实际调控能力限制而有界，并且能效为大于0的正数，因此，内层循环会迭代收敛到一个稳定值[16]。在外层循环，可以通过二分迭代算法求解最优µ*。综上，所提算法能够收敛[17]。

算法1 基于BCD的鲁棒波束赋形算法

图2 所提算法流程图

3.6 算法复杂度分析

基于文献[22]，本文的算法复杂度分析如下。假设问题式(32)解的精度为ε1，存在K个M×M维的矩阵变量， 8K个实数变量。因此，问题式(32)优化变量的阶数为n2=M2+8K。存在 2K个MN+1维线性矩阵不等式，K个M维线性矩阵不等式，5K个1维线性矩阵不等式。因此迭代次数的阶数为n1=ln(1/ε1)(KM(2N+1)+7K)1/2。问题式(32)的计算复杂度为

其中，m1=(MN+1)32K+M3K+5K,m2=(MN+1)22K+M2K+5K。

同样地假设问题式(34)解的精度为ε2，存在K个N×N维的矩阵变量， 8K个实数变量。问题式(34)优化变量的阶数为a2=M2+8K。存在2K个MN+1维 线性矩阵不等式，1个N维线性矩阵不等式， 5K+N个1维线性矩阵不等式。因此迭代次数的阶数为a2=ln(1/ε2)(2K(M+1)+5K+2N)1/2。问题式(34)的计算复杂度为

其中，b1=(MN+1)32K+N3+5K+N,b2=(MN+1)22K+N2+5K+N。所以，总的计算复杂度为

4 仿真结果与分析

本节采用数值仿真验证本文鲁棒波束赋形算法的有效性。由于太赫兹频段存在严重的路径损耗，考虑一个近距离通信场景[1]。假设系统中有一个太赫兹基站位于(0,0)处，RIS位于(3,3)处，用户位于以(5,0)为圆心半径1.5 m的圆内。到达角和离开角服从 [-π/2,π/2]内的均匀分布，假设天线距离为半波长，收发机处的噪声功率相等σ2=,∀k。定义归一化不确定性上界。其他参数如表1所示。

表1 仿真参数

图3给出了固定信道不确定性时，所提算法的收敛特性，从图3可以看出系统能量效率随迭代次数增加而增加并在4次迭代以内收敛，说明本文算法具有较好的收敛性。同时当发射天线数M增加时，系统能效提高，这是因为发射天线增加可以提供额外的空间自由度降低系统功耗，使系统能效提高。

图3 系统能量效率与迭代次数关系

图4给出了固定发射天线数时，系统能量效率和RIS反射阵元数量N的关系。从图4中可以看出系统能效随反射阵元数量增加而提高，这是因为N增加可以提供更多RIS到用户反射路径，从而提高系统吞吐量，同时RIS阵元为低功耗元件，功率很小，所以系统能效提高。此外，随信道不确定性上界增大，信道估计误差增加，系统需要消耗一定功率克服信道估计误差所带来的影响，使系统速率降低，从而降低系统能效。

图4 系统能量效率与RIS反射阵元数量关系

图5给出了基站天线数M、归一化不确定上界ε与系统能量效率的关系。在不确定性上界ε确定时，随着基站发射天线数增加，提供了额外的空间自由度并能降低功耗，因此能效提高。在发射天线M确定时，系统能效随ε的提高而降低，这是因为ε增大，信道估计误差增大，系统需要消耗一定功率克服信道估计误差所带来的影响，从而使系统能效降低。此外，在M=2 时系统能效随ε增大而下降最快，这是因为更多发射天线能更容易实现接收机的鲁棒设计。同时，在固定M和ε时，系统能效随N增大而提高，这是因为N数量增加能提供更多RIS到用户反射路径，提高系统吞吐量，RIS阵元为低功耗元件，功率很小，所以系统能效提高。

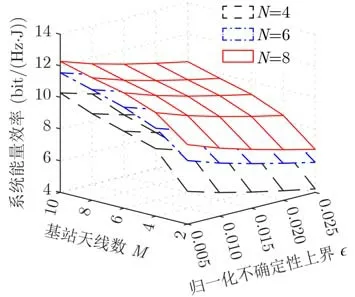
图5 系统能量效率与基站天线数和归一化不确定性上界关系

图6给出了量化比特与系统能量效率的关系。从图6可以看到RIS连续相位与离散相位之间的系统能效差距，系统能效随量化比特增加而增加，直到量化比特等于5时，RIS离散相位可以提供与连续相位等效的性能。

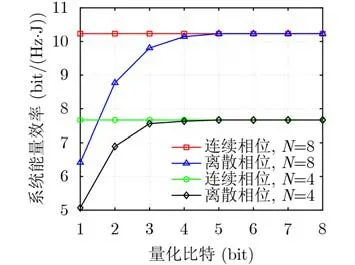
图6 系统能量效率与量化比特关系

图7给出了系统能量效率在L=2和L=4时与反射阵元数量关系。从图7可以看出，系统能效随N增长而增长，离散相位的系统能效低于连续相位，L越大，即使用的离散相位越多，与连续相位的差距越小，性能也会更接近连续相位。以N=8为例，当L=2时，性能损失3.813 bit/(Hz·J)，而L=4时，性能损失1.459 8 bit/(Hz·J)，说明连续相位是离散相位性能的上界。

图7 系统能量效率在 L=2 和 L=4时与反射阵元数量关系

图8给出了系统能量效率与信道不确定性上界的关系。从图8可以看出本文鲁棒波束赋形算法具有最高的系统能效，并且基于随机相位的波束赋形算法系统能效最低，随着归一化不确定性上界ε增大，信道估计误差增大，系统需要消耗一定功率克服信道估计误差所带来的影响，从而使系统能效降低。

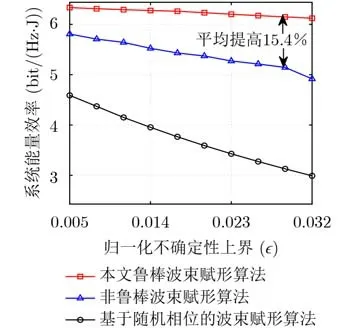
图8 系统能量效率与归一化不确定性上界关系

图9给出了不同算法的用户中断概率图，从图9可以看出本文鲁棒波束赋形算法的用户中断概率最低，说明其具有较好的鲁棒性。基于随机相位的波束赋形算法的用户中断概率最高，是因为RIS相位未能得到最优解。当归一化不确定性上界增大时，估计误差越来越大，获取信道状态信息更加偏离真实值，所以用户中断概率会增加。

图9 用户中断概率与归一化不确定性上界关系

5 结论

本文针对RIS辅助的太赫兹下行通信系统波束赋形问题进行研究。考虑基站的最大发射功率约束、RIS离散相移约束、每个用户的最小速率约束，以及不完美CSI约束，建立了一个多用户系统能效最大的波束赋形问题。针对该变量耦合的非凸优化问题，利用丁克尔巴赫和BCD将原问题分解为两个子问题，并引入连续凸近似、S-过程、半正定松弛、相位映射将两个子问题转化为等价的凸优化问题进行交替求解。仿真结果表明本文波束赋形算法具有较好的能效和鲁棒性。