高烈度震区大跨径中承式钢箱系杆拱桥减隔震技术研究
孙建鹏, 李进斌, 徐伟超, 王 毅, 于 超
(1. 西安建筑科技大学 土木工程学院,西安 710055; 2. 中国铁建大桥工程局集团有限公司,天津 300300;3. 中国启源工程设计研究院有限公司,西安 710018
拱桥是我国历史悠久的一种桥梁,已有近3 000年的发展历史。现如今,我国拱桥建设已跻身世界前列,跨度刷新了一个又一个纪录。尤其近几年随着我国西部大开发战略的推进,越来越多的大跨钢拱桥建设完成,但由于西部处于我国典型的强震多发区,桥梁在地震中遭受的破坏更为严重[1]。因此,为了提高桥梁抗震性能,确保桥梁在高强度地震来临时的安全性,对钢拱桥减隔震研究变得迫在眉睫[2]。
对于大跨拱桥这种特殊桥梁,在地震作用下结构受力较为复杂,产生的灾害是非常大的,因此许多国内外学者对这一领域进行了长期深刻的研究,已取得丰硕的成果[3-7]。李兆祥等[8]利用反应谱法研究了钢拱桥在地震作用下的抗震性能,指出在不同烈度的反应谱输入下,拱圈的最大剪力,最大弯矩发生在拱脚附近;夏修身等[9]通过对国内外典型大跨拱桥地震破坏原因的分析,对大跨拱桥的抗震概念设计的一般需求进行了讨论;Huang等[10]以某中承式钢拱桥为例,进行了一致和非一致激励地震相应研究,指出钢管混凝土拱肋结构的地震响应与输入波谱的卓越频率、范围和峰值大小密切相关;唐利科[11]以广西柳州官塘大桥为对象,开展了该桥梁的动力性能和减振性能的研究,提出两种减隔震措施布置方案;Xu等[12]对钢拱桥钢板内焊缝的超低周疲劳损伤效应对结构的地震影响进行了分析,指出随着拱肋钢板厚度的增加,钢拱桥的局部稳定性显著提高;罗红枝等[13]运用反应谱法与时程分析法,研究了两座不同形式的钢拱桥在不同地震动输入下的地震反应,结果表明横向地震作用不仅引起拱肋的面外内力,还会在拱肋内引起较大的面内弯矩、剪力和轴力;赵唯坚等[14]利用ABAQUS软件,分析了当矢跨比变化时桥梁的动态性能,指出矢跨比对拱桥自振周期及稳定系数影响较大,随着矢跨比减小,拱桥面外一阶稳定系数先增大后减小;张永亮等[15]基于SAP 2000有限元软件对上承式钢拱桥进行一致一维和多维激励,判断拱桥最不利位置; Jacob等[16]利用Midas Civil与ABAQUS有限元软件对大跨钢拱桥进行了模态分析,结果证实了Midas Civil软件的可靠性;杨灿等[17]以某大跨钢箱桁拱桥为背景,进行了地震响应分析,并确定了合理抗震体系。
通过上述研究看出,国内对大跨钢拱桥的地震响应研究已较为丰富,唯独缺乏高烈度震区依托工程建设的钢拱桥抗震案例。基于此,本文以一座位于高烈度震区的大跨径中承式钢箱系杆拱桥为工程背景,探讨不同支座对结构的减隔震效果,确定适合该桥的最优抗震体系。
1 有限元模型
1.1 工程概况
西双版纳黎明大桥横跨澜沧江,位于澜沧江与流沙河交汇之南[18]。主桥跨径布置:(65+310+65)m,主桥为直线,两侧引桥面为弧形,拱轴线为悬链线,矢高为77.5 m,矢跨比1/4。主梁采用钢混组合格构梁体系,主纵梁、次纵梁与横梁为工字型截面,其中横梁中部梁高2.0 m,主纵梁梁高1.806 m及次纵梁梁高0.8 m,混凝土桥面板厚度25 cm。桥位区场地类别为П类,场地分组属第三组,特征周期为0.45 s,抗震基本烈度为Ⅷ度,地震基本加速度为0.2g。
主桥的静动力计算模型采用MidasCivil2020空间有限元模型,梁单元模拟了主梁、拱肋、拱座和支柱,桁架单元模拟了系杆和吊杆。桥梁模型共有4 269个梁单元,140个桁架单元及696个板单元。共有3 698个节点。其拱桥立面图、平面图及模型如图1~图2所示。
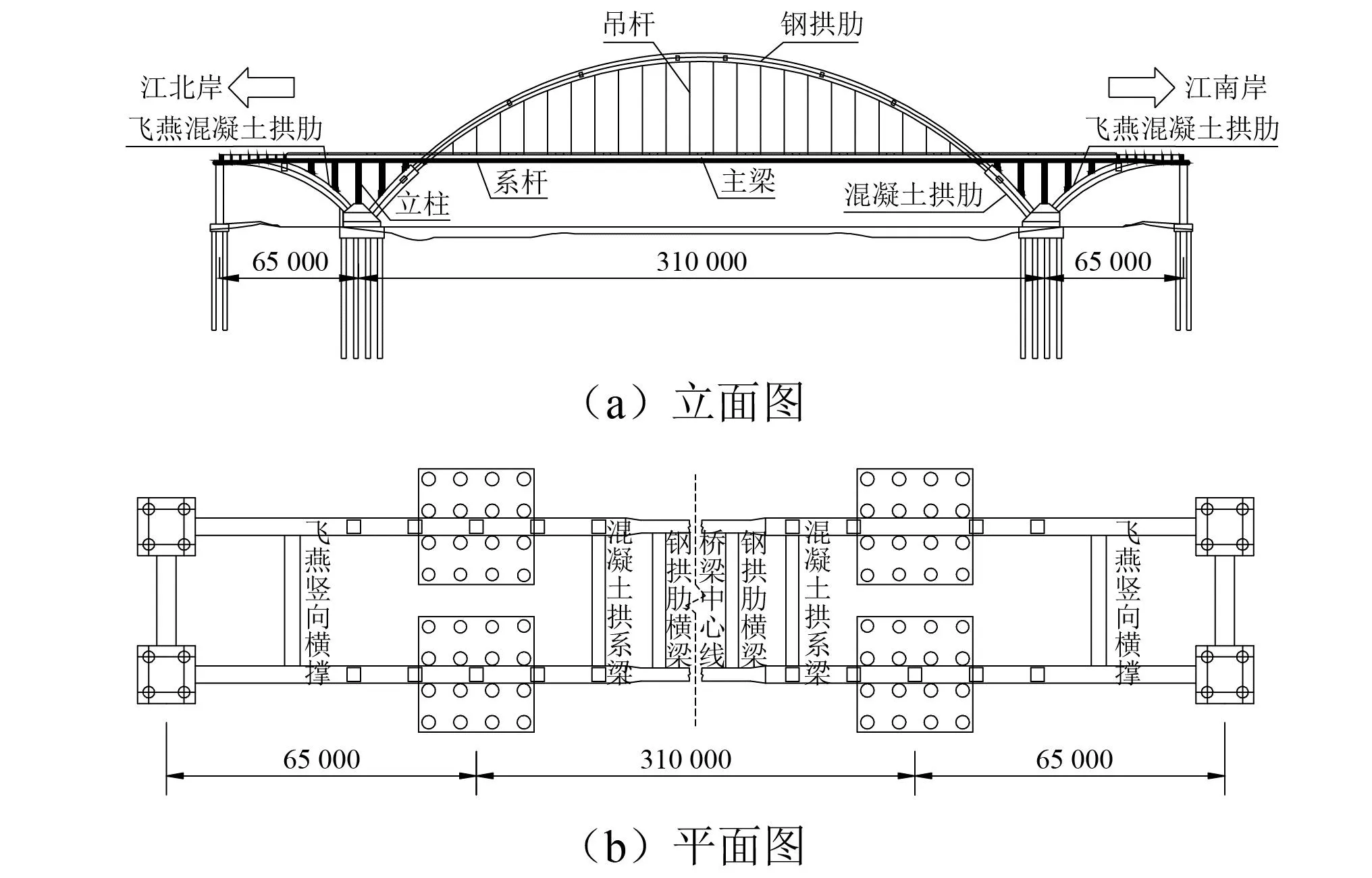
图1 黎明大桥桥跨布置图(mm)Fig.1 Bridge span layout of Liming Bridge (mm)

图2 主桥有限元模型Fig.2 Finite element model
1.2 边界模拟
全桥边界约束根据实际情况模拟,如图2所示。主桥过渡墩及立柱顶部支座采用弹性连接模拟其约束情况;飞燕、主拱肋混凝土段与拱座固结;钢主梁与拱肋连接处支座采用弹性连接来模拟;钢主梁和混凝土主梁梁端除纵桥向不设约束外,其他方向均设置约束;采用“土弹簧”来模拟桩土相互作用。为了进一步与实际约束相一致,需对模型反复调试直至接近实测模态,认为此模型效果较好。
1.3 地震波选取
根据桥址场地类型,本文在太平洋地震中心上选取了两条强震记录波,以及人工模拟一条波。并对所选的地震进行调幅处理,按5%阻尼比处理后的地震与目标反应谱的匹配结果如图3所示,地震加速度时程如图4所示,其中g为重力加速度。
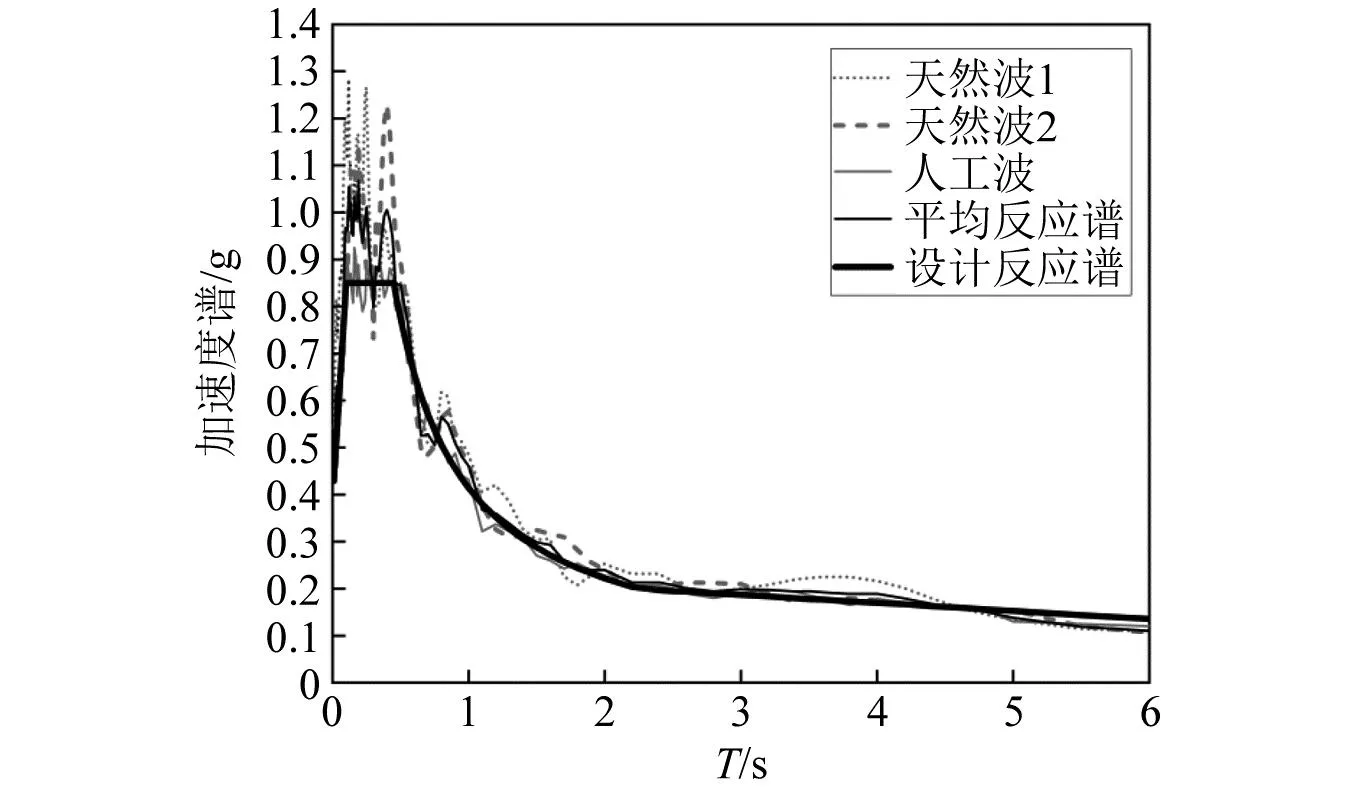
图3 地震波反应谱曲线Fig.3 Response spectrum curve of seismic wave
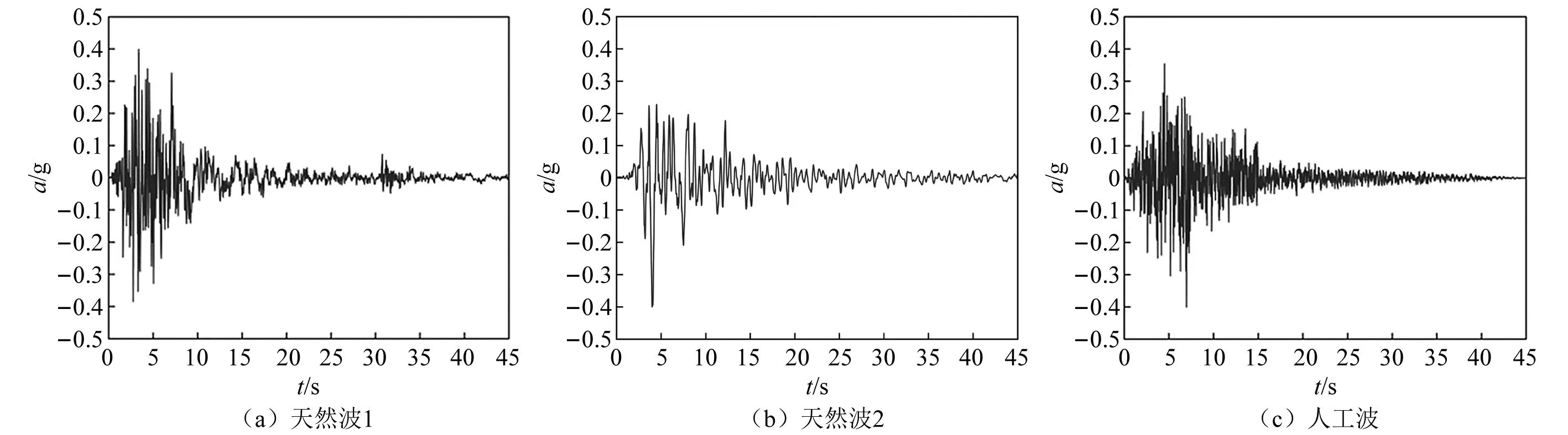
图4 地震波Fig.4 Seismic wave
2 减隔震技术研究
2.1 减隔震支座及原理
在高烈度震区的大跨拱桥遭受强大地震时,会产生非常大的变形和内力,对桥梁安全有不可忽视的影响。因此,为了最大程度降低这种隐患,常采用减隔震装置来实现[19]。设置减隔震装置的目的主要分为两个。其一是延长结构的基本周期,防止外部地震激励周期与结构自振周期相近,避免出现共振现象。如图5(a)所示,通过设置减隔震装置延长了自振周期,大幅控制了地震力但增大了结构位移。其二是增加结构阻尼来消散耗能,控制结构位移和内力。如图5(b)所示,通过设置阻尼器增加了结构阻尼,大幅降低了结构位移和动力加速度。
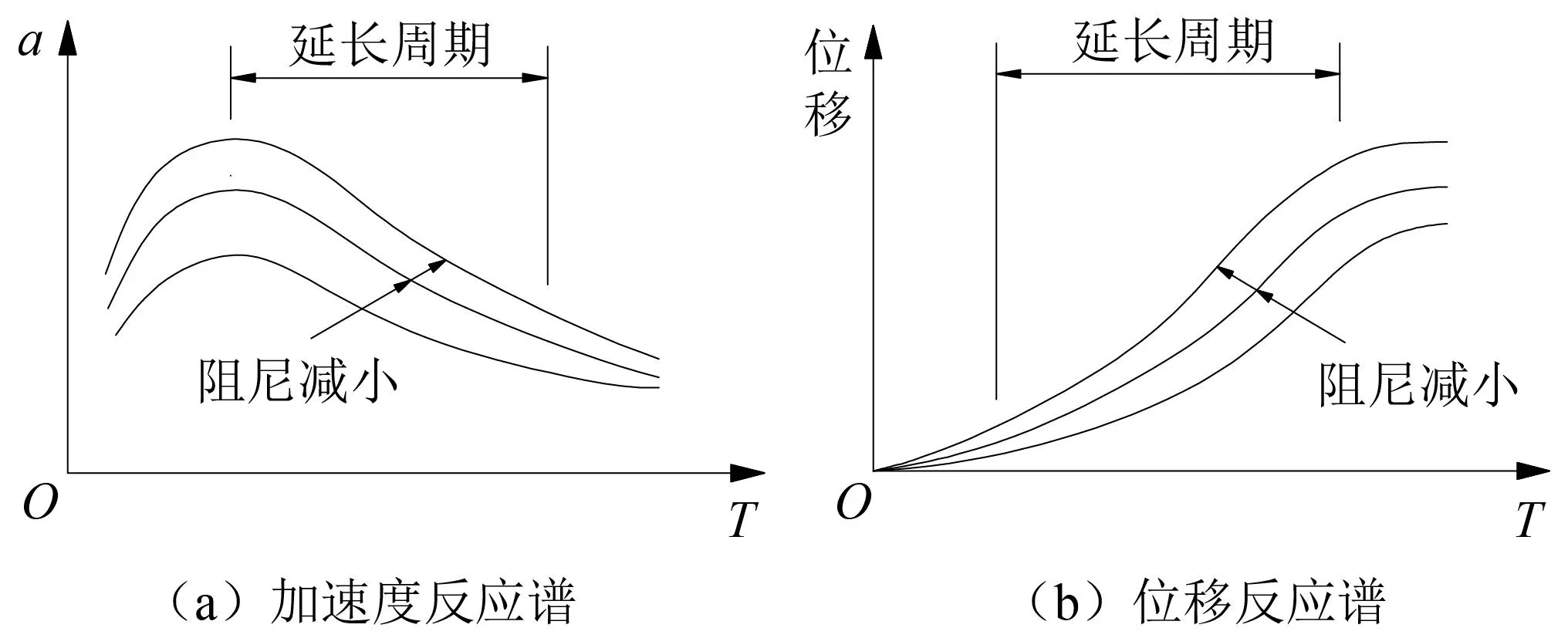
图5 减隔震原理Fig.5 Principle of seismic isolation
为了确定适合该桥的减隔震支座,本文分别建立三个工况模型。分别是:工况一,普通支座模型;工况二,铅芯橡胶支座模型;工况三,摩擦摆支座模型。通过对模型进行非线性时程分析,研究支座类型对桥梁结构的地震响应影响,探讨减隔震支座对于非隔震支座的减震敏感性。
2.1.1 铅芯橡胶支座力学性能
铅芯橡胶支座主要是利用铅芯的弹性支撑以及自身的塑性变形为主要耗能方式,具有更高的垂直承载力,更好的抗疲劳性能,更小的剪切强度[20]。对桥梁结构进行非线性静动力分析时的恢复力模型如图6所示。
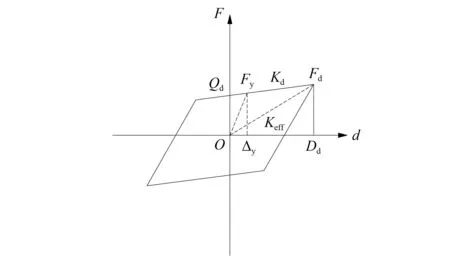
图6 铅芯橡胶支座恢复力模型Fig.6 Lead rubber bearing restoring force model
支座等效刚度为
(1)
支座等效阻尼比为
(2)
式中:Dd为水平设计位移,mm; Δy为屈服位移,mm;Qd为特征强度;Keff为等效刚度, kN/m;Kd为屈后刚度,kN/m。
2.1.2 摩擦摆支座力学性能
摩擦摆支座通过球面摆动延长结构自振周期实现隔震功能,工作机理类似钟摆原理,有良好的自复位能力,是一种经济优越、效率较高的隔震装置[21-22]。摩擦摆支座的恢复力模型如图7所示。
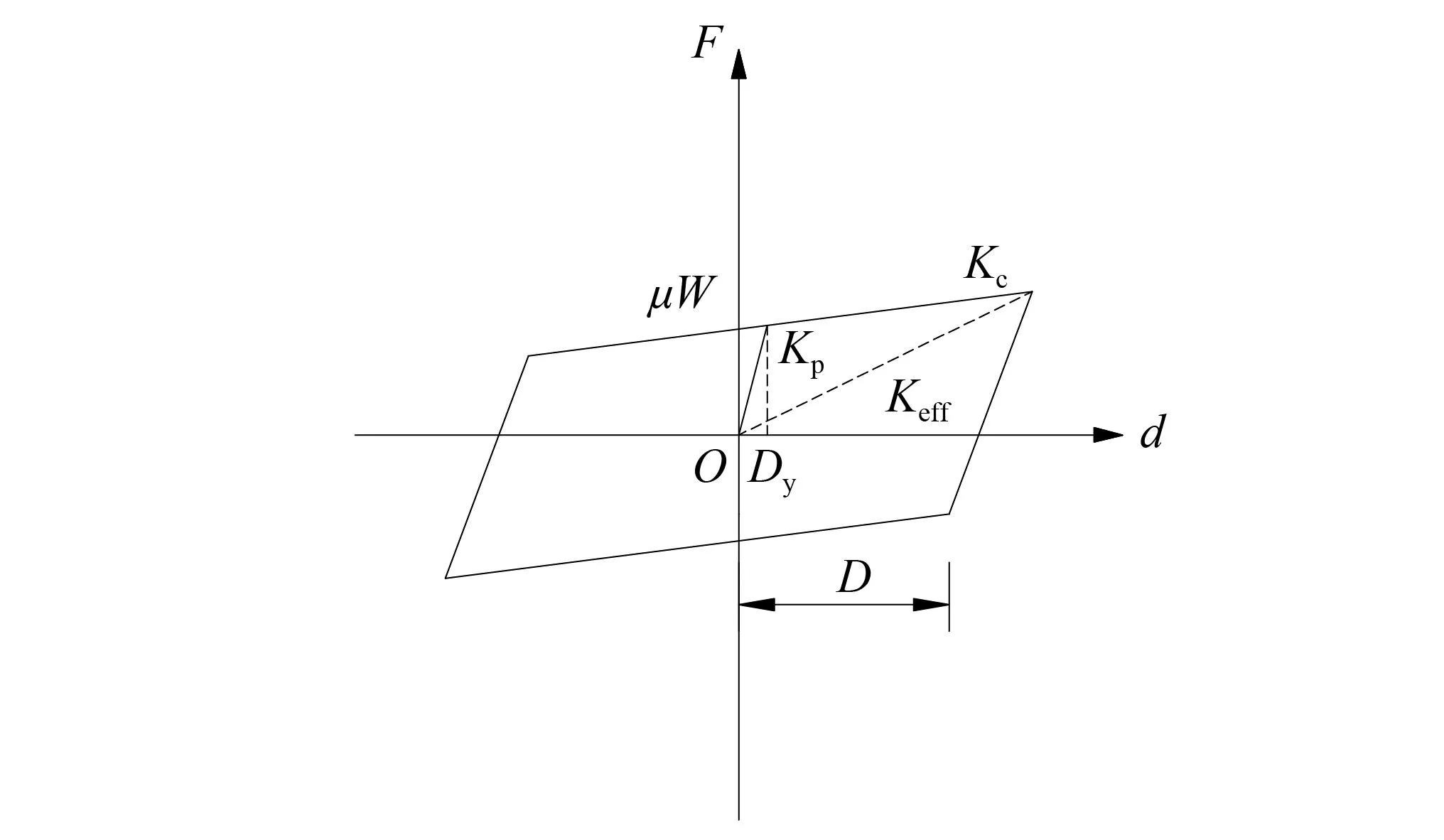
图7 摩擦摆支座恢复力模型Fig.7 Restoring force model of friction pendulum bearing
支座初始刚度为
(3)
支座等效刚度为
(4)
支座屈后刚度为
(5)
隔震结构的自振周期为
(6)
支座阻尼比为
(7)
支座恢复力为
(8)
式中:F为恢复力,kN;D为减隔震位移量,mm;R为曲率半径;dy为屈服位移,mm, 通常dy=2.5 mm;Kc为屈后刚度,kN/m;Keff为等效刚度,kN/m;Kp为支座初始刚度,kN/m;μ为动摩擦因数(建议取值0.05);W为竖向荷载,kN;ζe为阻尼比。
2.2 减隔震支座布置
全桥共设置32个减隔震支座。具体布置如图8所示。
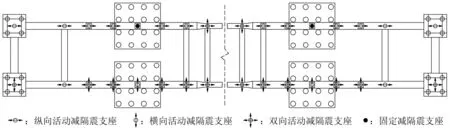
图8 减隔震支座布置图Fig.8 Seismic isolation bearing layout diagram
2.3 支座类型对拱桥结构的减隔震效果
为了清晰的认识到不同类型减隔震支座对拱桥的抗震效果,本文分别对采用普通支座(putong bearing,PTB)、摩擦摆减隔震支座(friction pendulum system,FPS)、铅芯橡胶支座(lead rubber bearing,LRB)的桥梁模型进行非线性时程分析,研究支座类型对桥梁结构的地震响应影响,探讨减隔震支座对于非隔震支座的减震敏感性,而衡量敏感性的度量值采用减震率。减震率=(减震前结构响应值-减震后结构响应值)/减震前结构响应值×100%。
2.3.1 位移减震效果
不同减隔震支座对结构位移响应的影响,如图9所示。由图9可知,减隔震支座的减震效果比较明显。其中,摩擦摆支座的减震效果整体优于铅芯橡胶支座,且位移减震率随着截面位置改变呈现不同的变化规律。由于设置减隔震支座,桥梁的柔性有显著的增加,但也增加了纵向位移,减震率绝对最大值在3/4拱肋处,为13.1%;横向位移有明显的降低,最大减震率在拱顶处,其值为55.6%;竖向位移降低幅度也较大,最大减震率在拱顶处,其值为44.6%。
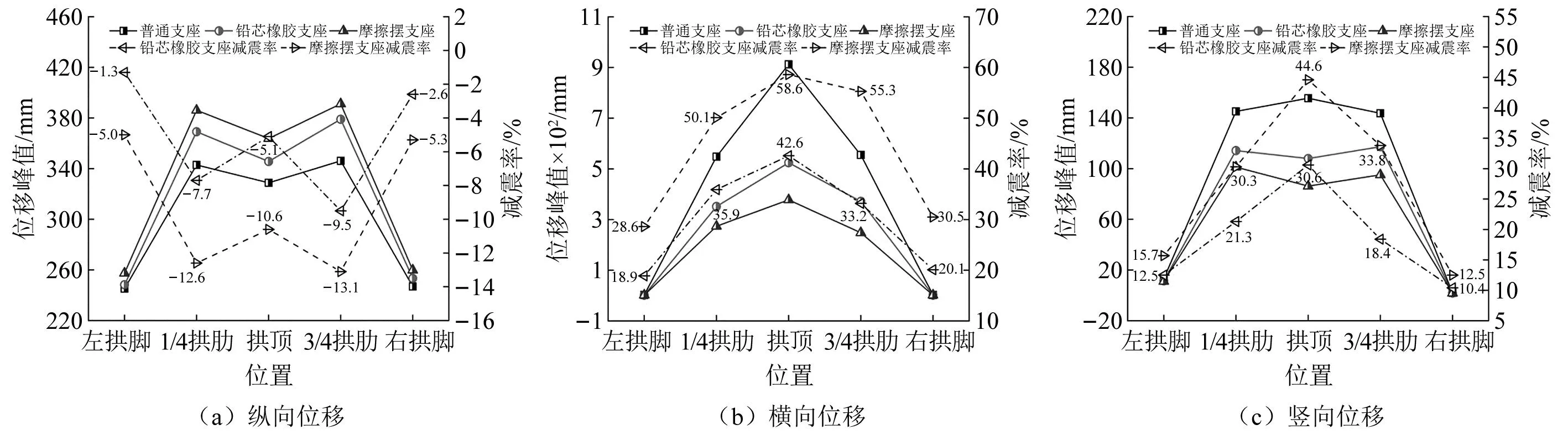
图9 不同减隔震支座对结构位移响应的影响Fig.9 The influence of different isolation bearings on structural displacement response
2.3.2 内力减震效果
不同减隔震支座对结构内力响应的影响,如图10所示。由图10可知,结构内力在设置减震支座后有明显的降低,摩擦摆支座模型的减震率普遍要强于铅芯橡胶支座模型。其中,轴力减震效果最佳处在摩擦摆支座模型的右拱脚,最大值为68.9%;面内弯矩减震效果最为明显,最大值在摩擦摆支座模型的左拱脚处,达到了77.1%;面外弯矩减震效果最佳处在右拱脚,为64.1%。
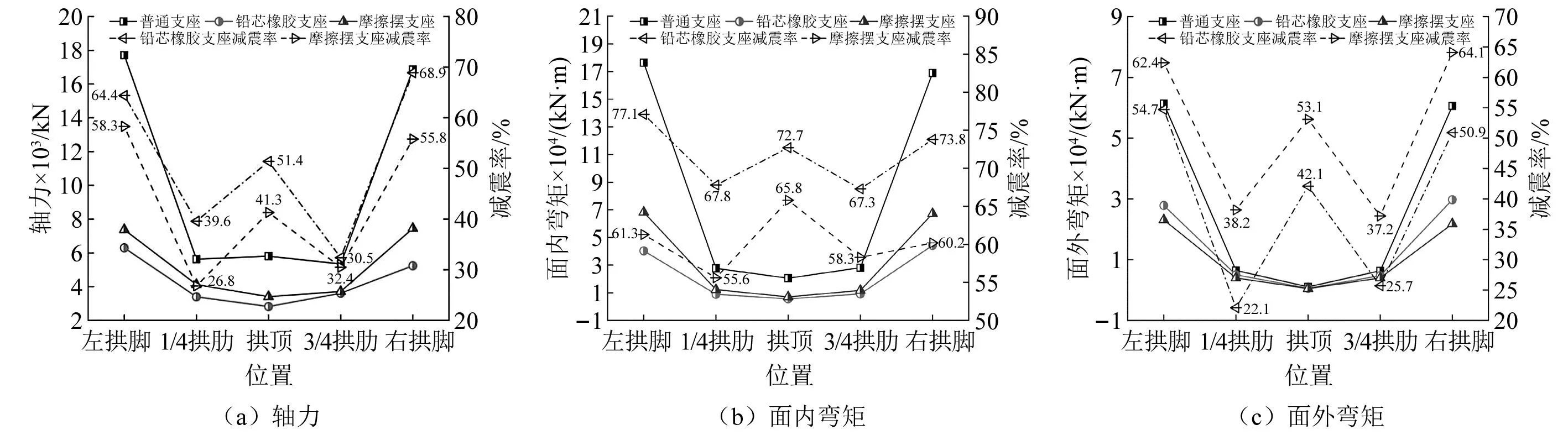
图10 不同减隔震支座对结构内力响应的影响Fig.10 The influence of different isolation bearings on structural force response
综上可知,从整体看减震效果由大到小依次排序为摩擦摆支座>铅芯橡胶支座>普通支座。但在设置减隔震支座后,桥梁的位移有不同程度的增大,甚至会产生落梁的危害,所以为了确保桥梁能抵御强地震的安全性,还需要对减震体系进一步完善。
2.4 基于摩擦摆支座联合黏滞阻尼器的减隔震效果
2.4.1 黏滞阻尼器力学
液体黏滞阻尼器是通过活塞杆在钢制圆筒中作往复运动,将地震力转化为往复运动的热能,达到减震消能的目的[23]。液体黏滞阻尼器的力学模型如图11所示。
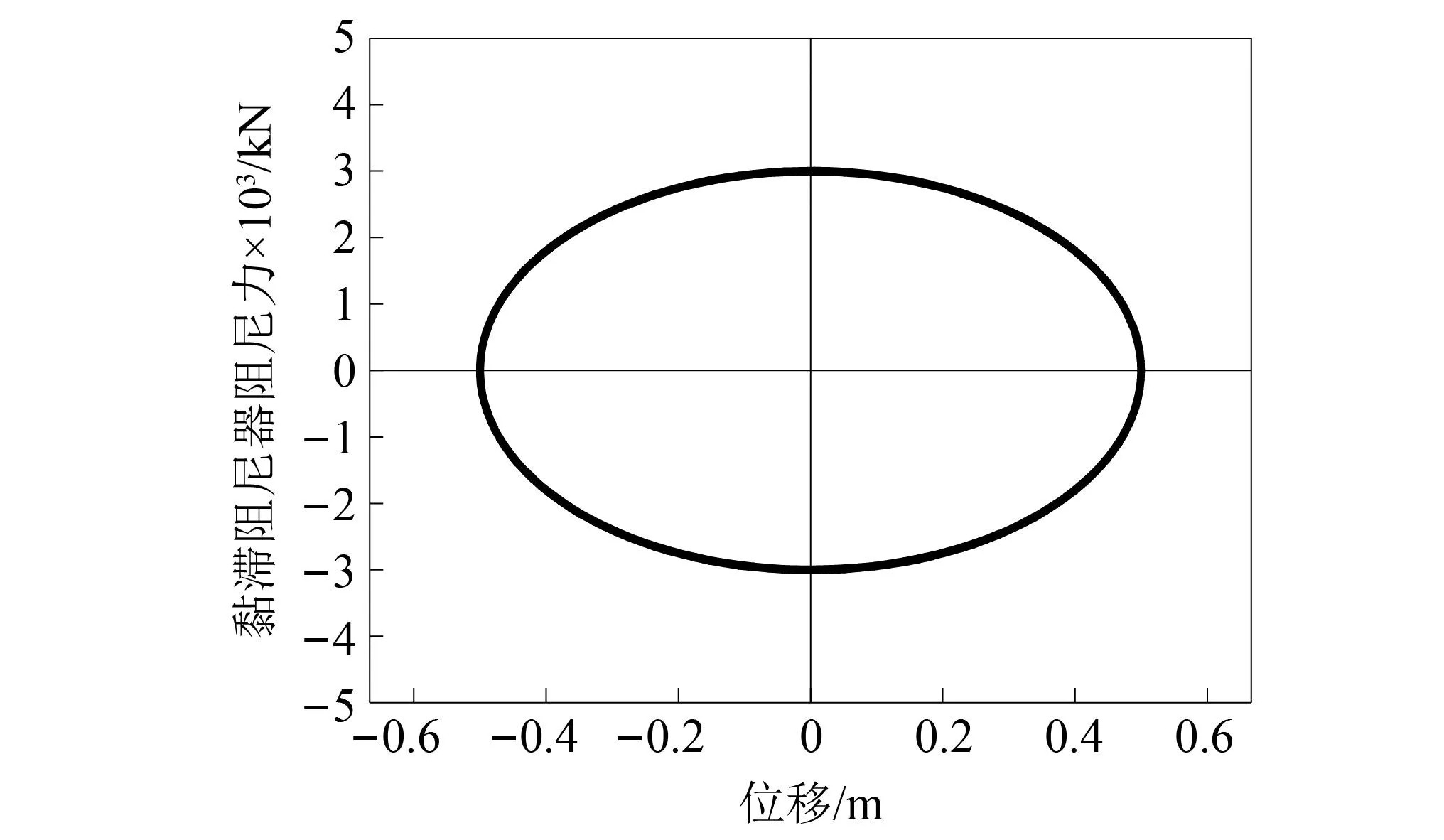
图11 黏滞阻尼器力学模型Fig.11 Mechanical model of viscous damper
F=CVα
(9)
式中:F为阻尼力;C为阻尼系数;V为阻尼器的相对运动速度;α为阻尼指数, 常取值在0.2~1.0。
2.4.2 阻尼器设置
为了降低因设置摩擦摆支座而增大的结构位移,本文在主梁和拱肋横向联结系处设置4个纵向和4个横向阻尼器,以此来协助耗散地震能量,控制结构响应位移[24]。设置情况如图12所示。
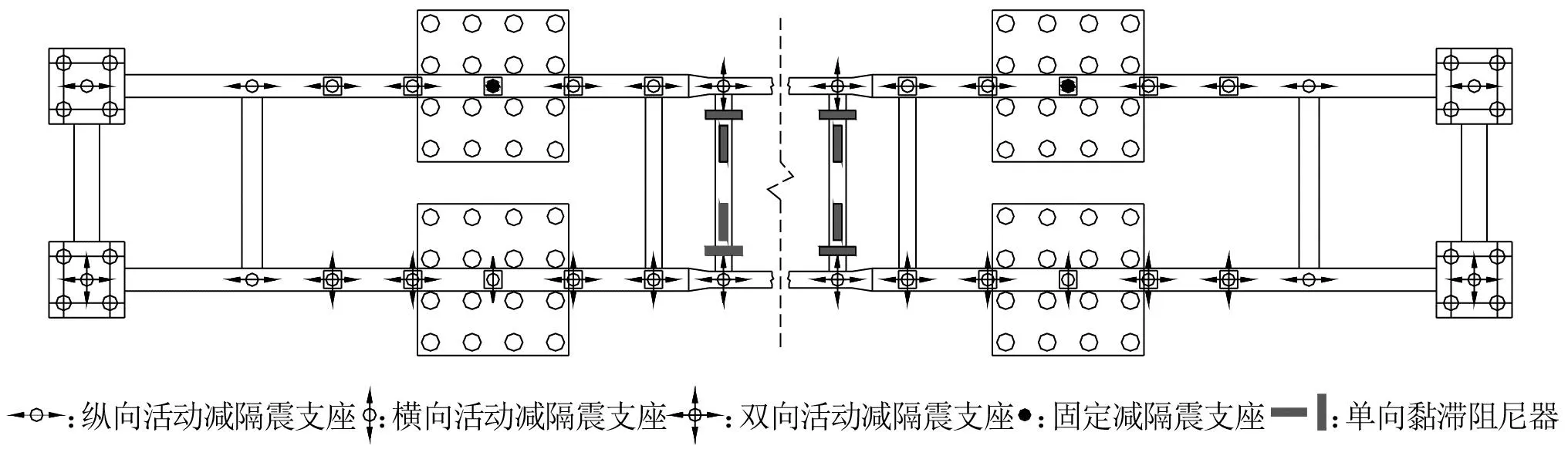
图12 阻尼器布置图Fig.12 Damper layout diagram
2.4.3 联合体系减震效果
联合抗震体系对结构位移的减震效果,如表1所示。联合体系的效果,如图13所示。通过表1和图13可知,联合减震体系对桥梁的纵向和横向位移有很大程度的降低,最大相对减震率均在拱顶,分别为26.2%和27.7%。表明在多维激励下,设置阻尼器能够有效降低纵向和横向位移。
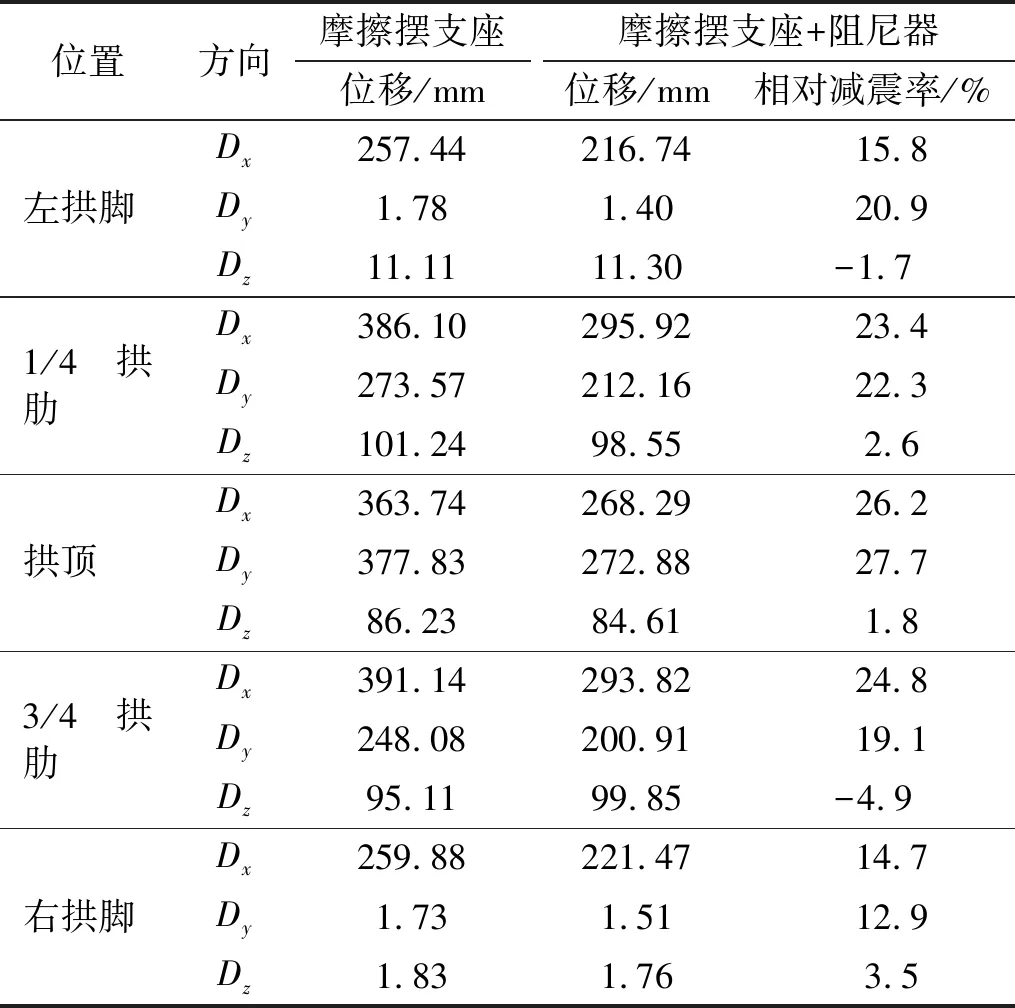
表1 联合抗震体系对结构位移的减震效果
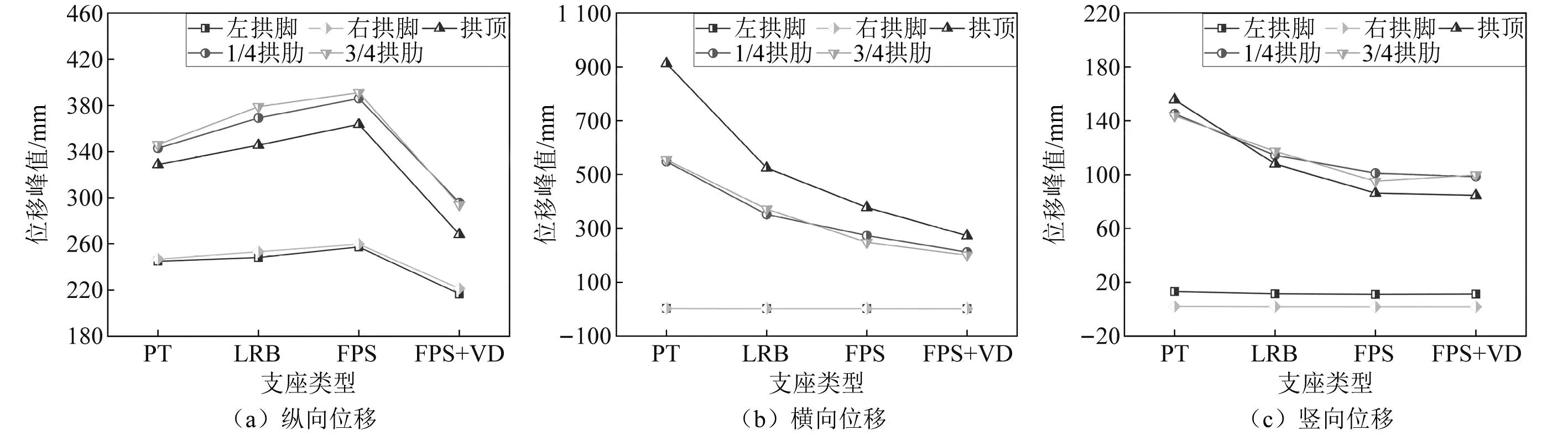
图13 联合体系的减震效果Fig.13 Damping effect of combined system
由此可说明阻尼器可以配合摩擦摆支座进行消能,能进一步提升桥梁的抗震性能,进而优化了此类桥梁的减隔震体系。
3 参数敏感性分析
为了节约成本,从支座合理性、经济性角度考虑,需进行减隔震装置参数敏感性分析,以此来确定合理的参数区间,使抗震体系的减隔震效果达到最大化。因此本文分别对摩擦摆支座及黏滞阻尼器的重要参数进行敏感性分析。
3.1 摩擦摆支座参数敏感性分析
摩擦因数、曲率半径是摩擦摆支座减震的重要参数。为了分析摩擦摆支座参数对桥梁结构地震响应的影响,同时也为了考虑支座的经济性,本节分别设置曲率半径为2 200 mm、3 200 mm、4 200 mm、5 200 mm、6 200 mm,摩擦因数为0.02、0.03、0.04、0.05、0.06。通过在有限元模型中变参分析得到散点数据值,利用MATLAB软件拟合获得参数变化对结构地震响应的拟合曲面。
3.1.1 位移敏感性
摩擦摆支座参数敏感性位移拟合曲面,如图14所示。由图14可知,纵向位移拟合曲面整体平滑,变化趋势稳定。主要表现为:在相同曲率半径下,纵向位移随摩擦因数的增大而减小;在相同摩擦因数下,纵向位移随曲率半径的增大先减后增,临界值在3 200 mm。横向位移拟合曲面与纵向位移拟合曲面有相似的变化趋势。竖向位移拟合曲面整体呈“W”形状,变化较为复杂。具体为:在相同曲率半径下,竖向位移随摩擦因数的增大而减小;在相同摩擦因数下,竖向位移随曲率半径的增大先减后增,再减小再增大,证明曲率半径对竖向位移的影响分区域影响。
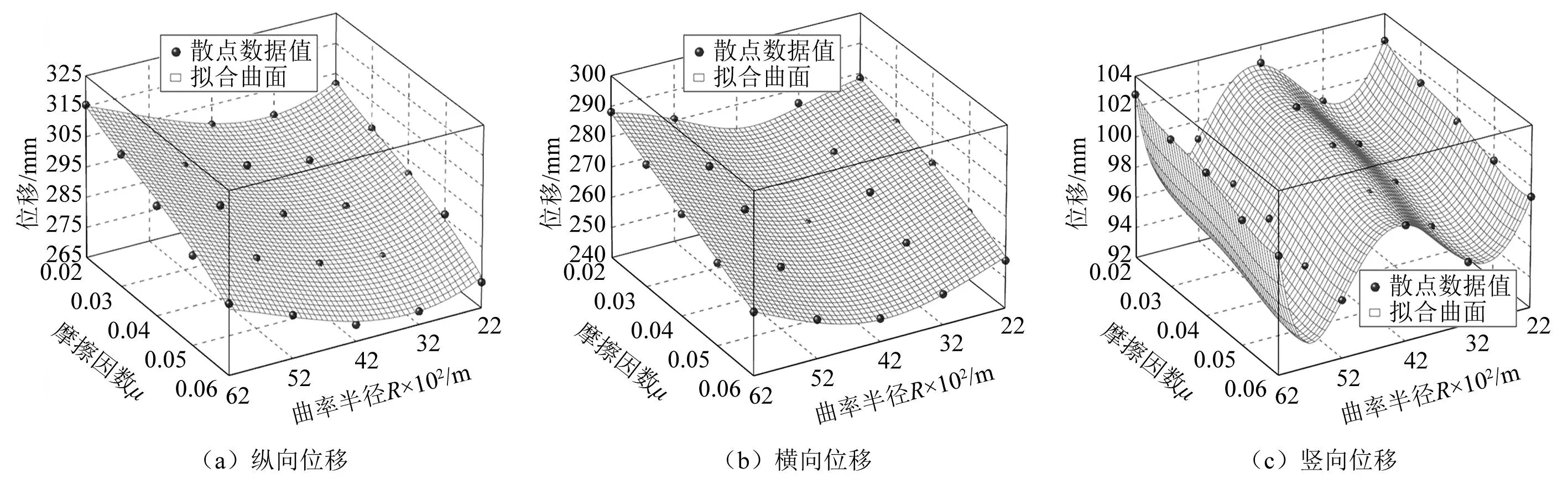
图14 摩擦摆支座参数敏感性位移拟合曲面Fig. 14 Friction pendulum support parameter sensitivity displacement fitting surface
由此可知,位移在双参数变化下合理的范围是:曲率半径一定时,摩擦因数在0.04~0.06,摩擦因数一定时,曲率半径在2 200~4 200 mm。
3.1.2 内力敏感性
摩擦摆支座参数敏感性内力拟合曲面,如图15所示。由图15可知,内力拟合曲面整体呈现凹状,四边高中间低,且曲面曲率整体均较大,参数变化对结构内力响应的影响较强。具体变化为:在相同曲率半径下,轴力和弯矩随摩擦因数的增大先减后增,临界值均在0.03;在相同摩擦因数下,轴力和弯矩随曲率半径的增大先减后增,临界值分别在4 200 mm和5 200 mm。

图15 摩擦摆支座参数敏感性内力拟合曲面Fig.15 Friction pendulum support parameter sensitivity internal force fitting surface
由此可知,内力在双参数变化下合理的范围是:曲率半径一定时,摩擦因数在0.02~0.04,摩擦因数一定时,曲率半径在3 200~5 200 mm。
3.2 阻尼器参数敏感性分析
为了优化阻尼器的减震效果,确定该桥合理的阻尼器参数,本文主要考虑阻尼系数和阻尼指数对结构地震响应的影响。设置的阻尼系数为2 000、4 000、6 000、8 000、10 000,阻尼指数为0.2、0.3、0.4、0.5、0.6。利用有限元模型确定散点数据值,采用MATLAB软件拟合得到参数敏感性曲面。
3.2.1 位移敏感性
摩擦摆支座参数敏感性位移拟合曲面,如图16所示。由图16可知,位移拟合曲面整体呈左低右高趋势,曲面较光滑,变化平稳,证明阻尼器参数变化对结构位移的控制效果影响较大。参数影响具体为:在相同阻尼系数下,结构位移随阻尼指数的增大先减后增,临界值在0.3;在相同阻尼指数下,结构位移随阻尼系数的增大而减小。
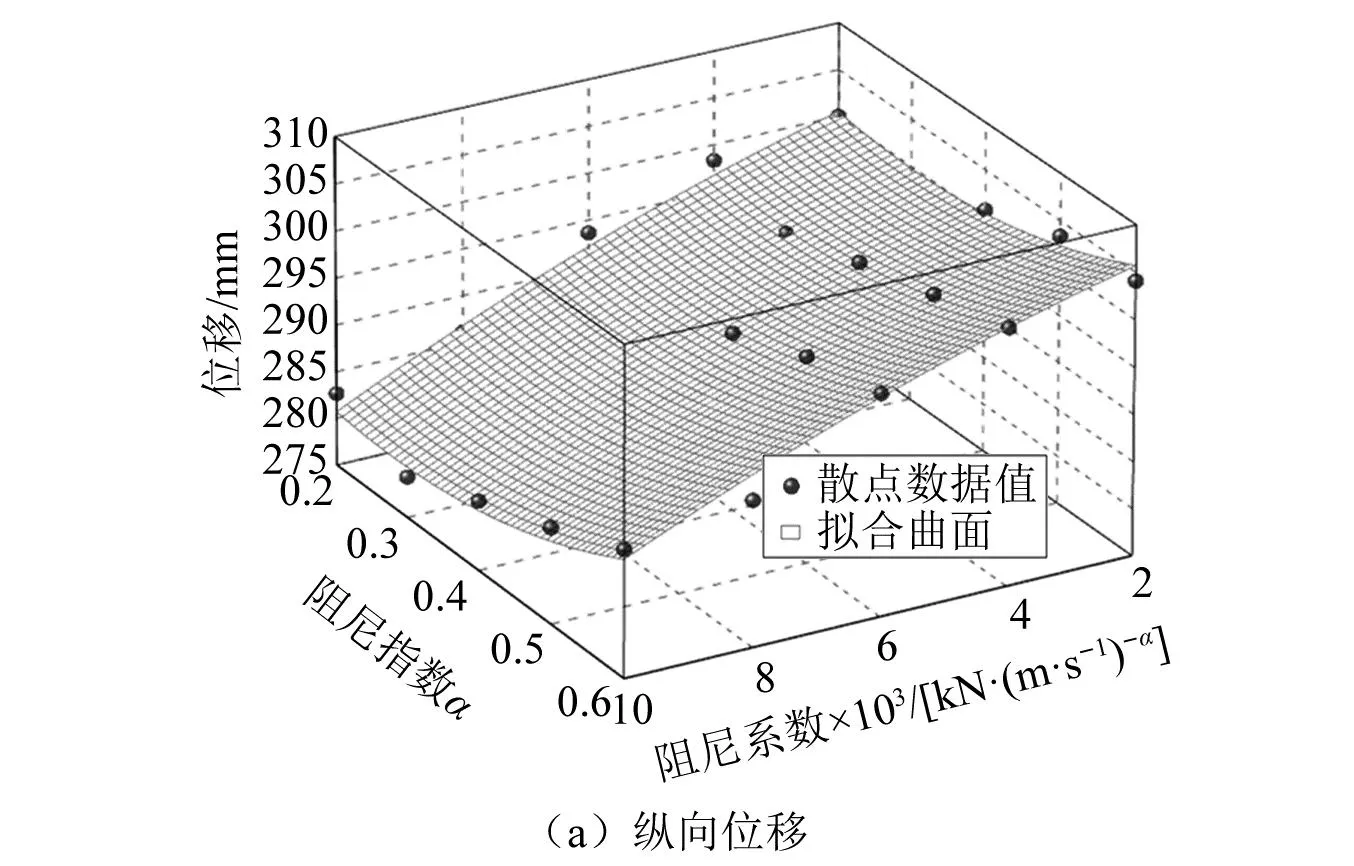
图16 摩擦摆支座参数敏感性位移拟合曲面Fig.16 Viscous damper parameter sensitivity displacement fitting surface
由此可知,位移在双参数变化下合理的范围是:阻尼系数一定时,阻尼指数在0.2~0.4,阻尼指数一定时,阻尼系数在6 000~8 000。
3.2.2 内力敏感性
摩擦摆支座参数敏感性位移拟合曲面,如图17所示。由图17可知,参数变化对结构内力地震响应影响比较复杂,整体呈现左低右高,拟合曲面存在波浪状。具体为:在相同阻尼系数下,轴力和弯矩随阻尼指数的增大先减后增,临界点均在0.3;而在相同阻尼指数下,轴力和弯矩随阻尼系数的增大而减小。
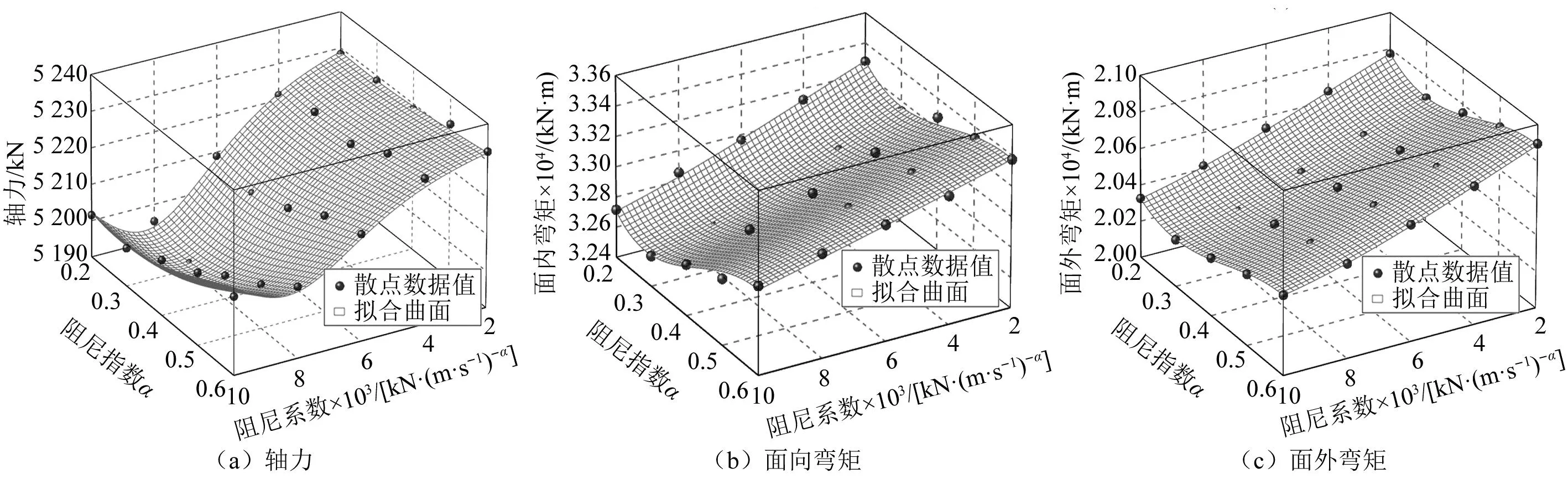
图17 摩擦摆支座参数敏感性位移拟合曲面Fig.17 Viscous damper parameter sensitivity internal force fitting surface
由此可知,内力在双参数变化下合理的范围是:阻尼系数一定时,阻尼指数在0.2~0.4,阻尼指数一定时,阻尼系数在4 000~6 000。
综上,本节分别研究了摩擦摆支座参数变化对结构响应的影响以及阻尼器参数变化对结构响应的影响,分别确定了最佳的减震参数范围。基于此,从结构变形和内力整体性考虑,摩擦摆支座联合黏滞阻尼器参数敏感性最佳的变化范围是:摩擦因数达到0.04,曲率半径达到3 200~4 200 mm,阻尼指数达到0.2~0.4,阻尼系数达到6 000。
4 最优抗震体系减隔震效果
结合上述研究内容,黎明大桥最优的抗震体系为基于摩擦摆支座联合黏滞阻尼器减震,在此基础上确定适用于该桥的最佳参数,结构的位移和内力显著降低,抗震体系起到良好的减震效果[25]。
大跨中承式钢箱系杆拱桥在地震作用下,由于地震波到达桥梁各支撑点的时间不一致,将产生相位差(即行波效应)[26]。地震波的传播速度对结构的影响较大,作者选取视波速200 m/s、500 m/s和1 000 m/s,采用相对运动法分析行波效应作用下结构的地震响应,发现随着视波速的增大,结构的响应趋向于一致激励下的情况,因此,本章行波效应的视波速为200 m/s。
地震波不仅具有较强的随机性,同时具有明显的序列性。震害资料表明,在一次强烈的主震过后,通常会伴随有多次余震的发生,且余震造成的二次破坏不应被忽视[27]。本章是以天然波1为基础,通过震级衰减关系得到主余震加速度峰值比,最后确定主余震序列波。主余震序列波如图18所示。
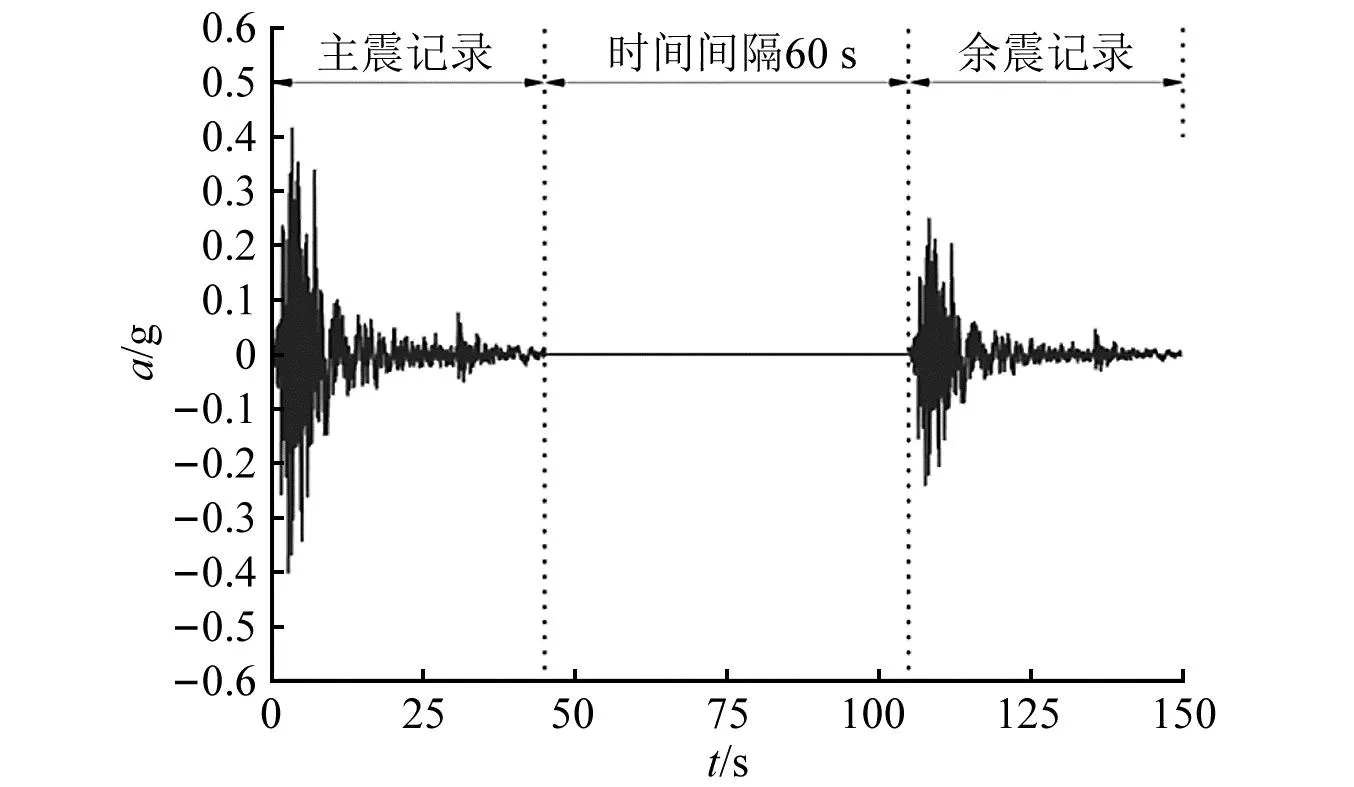
图18 主余震序列波Fig.18 The main aftershock sequence wave
为了验证在危险地震作用下最优抗震体系的减震效果,本节采用两种危险地震工况:工况一,行波效应;工况二,主余震序列波作用。
4.1 行波效应
行波效应下最优抗震体系的减隔震效果,如图19所示。由图19可知,桥梁在最优抗震体系下结构的变形和内力得到了很好的控制,位移最大减震率截面在拱顶处,其值为71.6%;弯矩最大减震率截面在右拱脚处,其值为81.5%。关键截面位移和内力的显著降低,大大地减小了桥梁结构的地震损伤,增大了桥梁抵抗危险地震的能力。将最优抗震体系应用于该种桥梁,会在抗震设计层面补充了此类桥遭遇危险地震的设计案例。
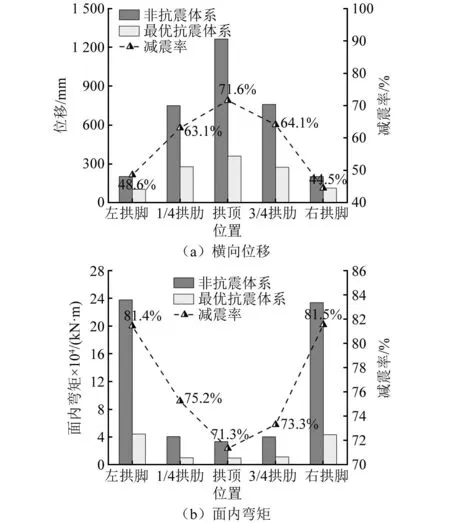
图19 行波效应下最优抗震体系的减隔震效果Fig.19 Seismic isolation effect of optimal seismic system under traveling wave effect
4.2 主余震序列波作用
主余震序列下最优抗震体系的减隔震效果,如图20所示。由图20可知,在主余震序列波作用下,设置合理的抗震体系可以有效地减少桥梁的地震反应,减小强余震对结构造成的“二次损伤”。由图20可知,位移减震效果非常显著,最大减震率截面在拱顶处,为75.3%;弯矩最大减震率截面在左拱脚处,其值为82.3%。由于强余震的存在,加剧了结构的响应峰值,对结构形成了附加损伤。但采用合理的减隔震体系不仅能减小桥梁变形,而且能控制截面内力大小,进而提升了大跨拱桥抗震能力,同时为后续学者一种抵抗强余震对结构损伤的抗震方法。

图20 主余震序列下最优抗震体系的减隔震效果Fig.20 Seismic reduction and isolation effect of the optimal seismic system under the main aftershock sequence
5 结 论
为了研究高强度地震下大跨拱桥的抗震性能,本文以一座位于高烈度震区的大跨径中承式钢箱系杆拱桥为工程背景,采用非线性时程分析法,探讨不同支座对结构的减隔震效果,并通过参数敏感性分析,确定了适合该桥的合理抗震体系。具体结论如下:
(1) 通过分析普通支座、摩擦摆支座、铅芯橡胶支座对桥梁结构的减隔震效果,分别探讨了不同支座对结构的减震敏感性,得出相比于普通支座,减隔震支座能够增强桥梁的柔性,有效地降低结构位移和内力,但纵向位移有所增加。从整体看,减震效果由大到小依次排序为摩擦摆支座>铅芯橡胶支座>普通支座。
(2) 通过对基于摩擦摆支座联合黏滞阻尼器的减隔震体系研究可知,设置阻尼器能够有效降低纵向和横向位移。表明阻尼器可以配合摩擦摆支座进行消能,能进一步提升桥梁的抗震性能,从而优化了此类桥梁的减隔震体系。
(3) 从节约成本,合理性角度考虑,对减隔震装置进行了参数敏感性分析,得出从结构变形和内力整体性考虑,联合抗震体系参数敏感性最佳的变化范围是:摩擦因数达到0.04,曲率半径达到3 200~4 200 mm,阻尼指数达到0.2~0.4,阻尼系数达到6 000。
(4) 为了验证最优抗震体系对危险地震作用下的减震效果,分别对行波效应模型及主余震模型进行了分析。研究可知在行波效应作用下桥梁结构的变形和内力得到了显著的控制,特别是横向位移和面内弯矩减震率较大;在主余震序列作用下,建立合理的抗震体系,可以减小拱桥在地震中的反应,降低强余震对结构造成的“二次损伤”。
(5) 大跨拱桥在最优抗震体系下,关键截面位移和内力均显著降低,大大地减小了桥梁结构的地震损伤,增大了桥梁抵抗危险地震的能力。这会在抗震设计层面补充了此类桥遭遇危险地震的设计案例,同时为后续学者提出一种抵抗强余震对结构损伤的抗震方法。

