网联自主车辆协作换道行为博弈特性及模型

姬利源, 曲大义, 戴守晨, 崔善柠, 李奥迪, 魏传宝

(青岛理工大学 机械与汽车工程学院, 青岛 266520)

0 引言

车联网系统多维度融合了人-车-路-环境各要素,车-车交互作用和车-路协作关系发生内在的结构性变化,网联自主车辆(connected autonomous vehicle, CAV)和人工驾驶车辆(human-driven vehicle, HV)在网联智能交通系统混行共存,称之为网联异质车群。在异质车群中,网联自主驾驶车辆和人工驾驶车辆互相渗透,共同完成道路行驶任务。

伴随着智能网联技术的发展,车辆换道相关理论和模型的发展也取得了很多研究成果。Gipps模型[1]是最早提出的一种基于微观观察描述决策过程和行为的换道模型。Prajwal等[2]把换道分为强迫(forced)换道、自由(free)换道和协作(cooperation)换道,对换道行为的机制和动力学原理进行了分析。王荣本等[3]使用最小安全距离作为安全换道的前提,为自动换道辅助系统提供了理论基础。刘小明等[4]使用动态重复博弈原理建立了车辆模型。Yu等[5]通过全面考虑周围的车辆以及相关的轨迹规划模型来建立车道决策模型。曲大义等[6]通过研究分析分子相互作用势与车辆交互关系,建立了车辆换道的分子动力学模型,展现了网联自主车辆的换道行为特性。

分析比较近期国内外研究结果可以看出,对车辆换道模型的研究主要着眼于换道轨迹和跟踪算法,并未对车辆之间的动态交互博弈关系进行深入探究。在智能网联交通环境下,车辆换道要同时考虑换道安全性和与周围车辆的交互博弈作用。本研究基于博弈论,对车辆行驶过程中车辆换道危险等级进行量化,使用车辆之前的发生碰撞的时间(time-to-collision, TTC)作为参数,通过对碰撞时间和设定阈值的比较来进行策略的选择,在此基础上结合车辆动力学建立了车辆换道的动态安全模型,瞄准决策后车辆的速度收益及目标车群的安全稳定性,提出了网联自主车辆协作换道动态博弈模型,使网联自主车辆更加安全、稳定地驾驶。

1 网联自主车辆协作换道行为动态博弈特性

1.1 协作式换道行为分析

换道和跟驰是车辆驾驶时最基本的2种行为。车辆换道时,周边的环境因素和驾驶者的心理因素等会对驾驶者换道行为决策产生影响。换道行为往往起源于驾驶者的意图和目标。而在异质车群中,智能网联自主车辆通过准确感知和识别不同类型的车辆以及周围的环境,为驾驶员换道的行为提供支持,从而成功换道。在智能网联技术支持下,自主车辆的换道多呈现为协作换道的形式,即2辆或多辆车辆共同合作,以确保安全地变换车道。这种行为通常是在高速公路或多车道道路上进行的,以允许车辆在不妨碍其他交通流的情况下改变自己的车道。

1.2 博弈策略分析

智能网联驾驶车辆在接收到周围的环境信息之后,车载决策单元对周围的状态信息进行一系列处理分析之后,产生最终决策。需要换道且会互相影响的2辆车采取博弈论的策略进行协作换道。

博弈是指在决策中涉及多方参与者在特定规则下做出策略选择,以追求自己的利益最大化或达成特定目标的过程。按照博弈者之间是否进行合作来分类,博弈可以划分为合作性博弈和非合作性博弈。博弈者不通过合作来达到博弈目的,这个博弈被称为非合作博弈。网联车是通过收集到的周围的信息来进行有利于自身的决策的,明显可以看出是非合作博弈,博弈类型划分见表1。

表1 博弈类型划分Tab.1 Classification of game type

因为本研究的参与者为网联自主车辆,在网联环境下双方选择策略及之后所产生的收益是透明的,所以博弈首先是一个完全信息博弈。在换道决策博弈中,参与者是同时制定换道策略并采取行动的。综上所述,本研究将建立一个完全信息静态博弈模型。

1.3 协作换道动态博弈策略的纳什均衡解

纳什均衡是指在2个及其以上的参与者的非合作的博弈中,假设每个参与者互相知道对方的均衡策略的情况下,只有同时改变博弈策略才会使收益变化的一个均衡解。在博弈论中,如果每个参与者选择自己的策略,且只有所有参与者同时改变策略时才能取得收益,那么当前的策略组合及其相应的结果构成了纳什均衡。

对于双人非合作静态完全信息博弈,记协作换道的参与者集为N={1,2},每个参与者的策略集为A1={c1,c2}和A2={r1,r2},u1、u2分别为2个参与者采取不同策略时的收益函数,u1(c1,r2)表示的是参与者1使用c1策略和参与者2使用r2策略时,参与者1产生的收益。2辆车协作换道博弈收益矩阵见表2[7]。

表2 协作换道博弈收益矩阵Tab.2 Cooperative lane change game payoff matrix

如果存在纯策略(cn,rn)使下式成立,则视策略(cn,rn)为纯策略的纳什均衡。

如果非合作博弈不存在纯策略纳什均衡,那么它的混合策略纳什均衡一定存在。混合策略纳什均衡表示的是多次博弈达到收益最大化时,选择各纯策略的概率估计,即每个纯策略对于博弈方的友好程度。非合作混合策略博弈收益矩阵见表3[8]。

表3 混合策略博弈收益矩阵Tab.3 Mixed strategy game payoff matrix

2个参与者的期望收益分别为

分别对p和q进行求导并使其导数为0,可得

由此可知,当纯策略博弈的纳什均衡不存在时,应采取混合策略博弈,并找到其纳什均衡。协作换道的纳什均衡能够使目标车辆相互合作协调来实现最优交通效率,提高协作换道模型的速度收益和稳定性。

2 协作换道博弈决策模型

在智能车联网的环境下,对车辆的协作换道进行建模,在以下假设中进行:车-车之间通信都是即时的;车辆所获信息包括自身与周边车辆的位置、速度、加速度以及地理环境等信息;所有车辆都为标准一致的轿车,且都是网联自主驾驶车辆,即不考虑差异性。

2.1 换道过程分析

在满足上述假设的情况下,忽略存在强制换道的场景,对协作换道过程进行分析。网联自主车辆协作换道示意图如图1所示,A、B、LA和LB分别代表目标车辆、目标车道后车、原车道的前车和目标车道的前车。

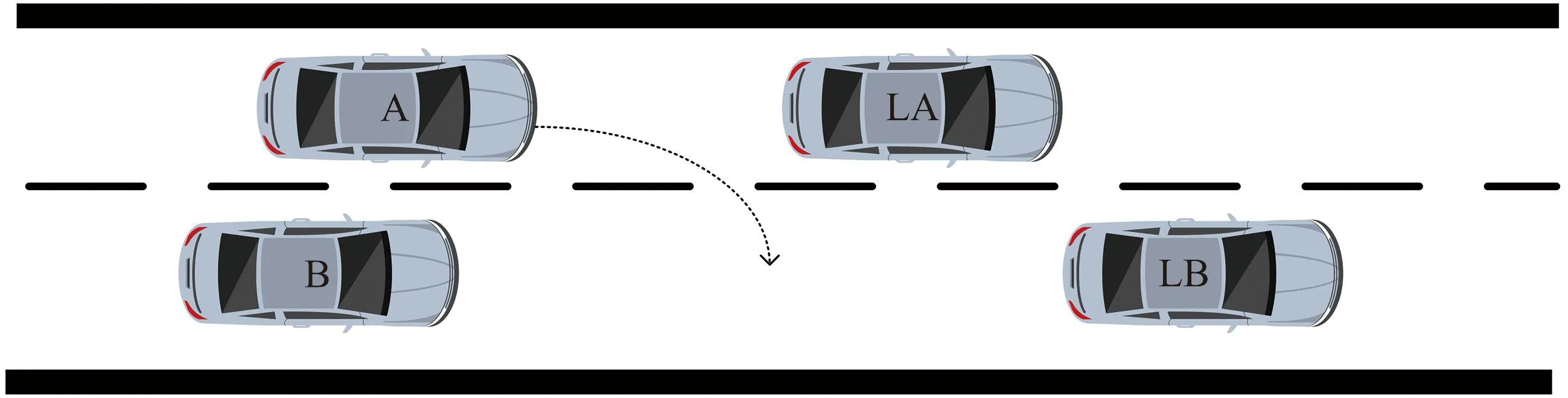
图1 网联自主车辆协作换道示意图Fig.1 Cooperative lane change process of connected autonomous vehicles

在智能车联网的环境下,目标车辆能获得当前车道前车和目标车道前车的速度,对目标车辆的换道意图进行简单量化。设目标车辆当前车道前车的速度为va,目标车道前车速度为vb。

(1)

用K来表示目标车辆的换道意图,通过原车道前车与目标车道前车的速度的比值,来判断换道意图。K>1时,目标车辆有速度增益,产生换道意图。K≤1时,目标车辆得不到相应的速度增益,无换道意图,在当前车道继续进行跟驰。

2.2 协作换道博弈模型

在产生换道意图之后,若能保证换道安全,则进行换道;若不能,则保持现状。碰撞时间 (TTC)是目标车辆与前车发生碰撞的时间,也是评价交通安全的重要指标之一。

在TTC模型中,整个换道行为被视为在二维平面中进行,车辆由在平面中用坐标表示的矩形代替。目标车辆与目标车道前车的矢量位置与速度关系如图2所示,O1、O2分别为目标车辆1、目标车道前车2的质心位置,质心之间的距离为D1,2,C1、C2为最可能碰撞点(即两车之间的最近点)的位置,最可能碰撞点之间的距离为d1,2。两车的位置关系可表示为(O1,O2,C1,C2),速度表示为(v1,v2)。

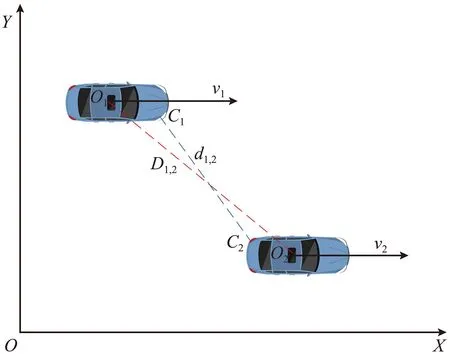
图2 目标车辆与目标车道前车的矢量位置与速度关系Fig.2 Relationship between vehicle position and velocity

如发生碰撞,碰撞点一般位于车辆的外缘,所以碰撞一般最先发生于两车距离最近的侧边点C1和C2,两点之间的距离为

(2)

可得

(3)

将式(3)两边同时微分,易得

d1,2d′1,2=(C1-C2)T(V1-V2),

(4)

由此可得出两车之间的相对速度-d′1,2。

基于式(4),可得目标车辆1与目标车道前车2的间隔距离的一阶导数为

(5)

由TTC的定义可知d1,2+d′1,2T=0(T为TTC的值),可得

(6)

把式(2)、(5)代入式(6)得

(7)

然后比较TTC阈值(T*)与TTC的关系,对车辆换道是否存在安全风险进行判断,一般为4 s或6 s,从换道的安全性来看使用6 s来作为判断换道是否存在风险的阈值。根据文献[9]对TTC数值与换道风险等级的关系划分,对TTC阈值不大于6 s的换道数据进行换道风险等级分析,得到换道时不同风险程度的风险阈值。

换道风险预警等级划分如图3所示。由图3可知,当T*<0.4 s时,换道有高风险;当0.4 s6.0 s时,换道基本无风险。为了保证在车联网情况下换道的安全,本文所用换道博弈模型在T*>6.0 s时,才会进行换道。安全阈值T*与速度以及距离关系如图4所示。

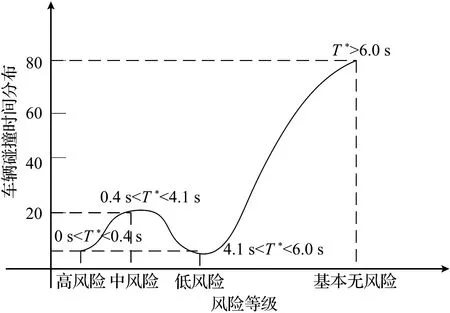
图3 换道风险预警等级划分Fig.3 Lane change risk warning level classification

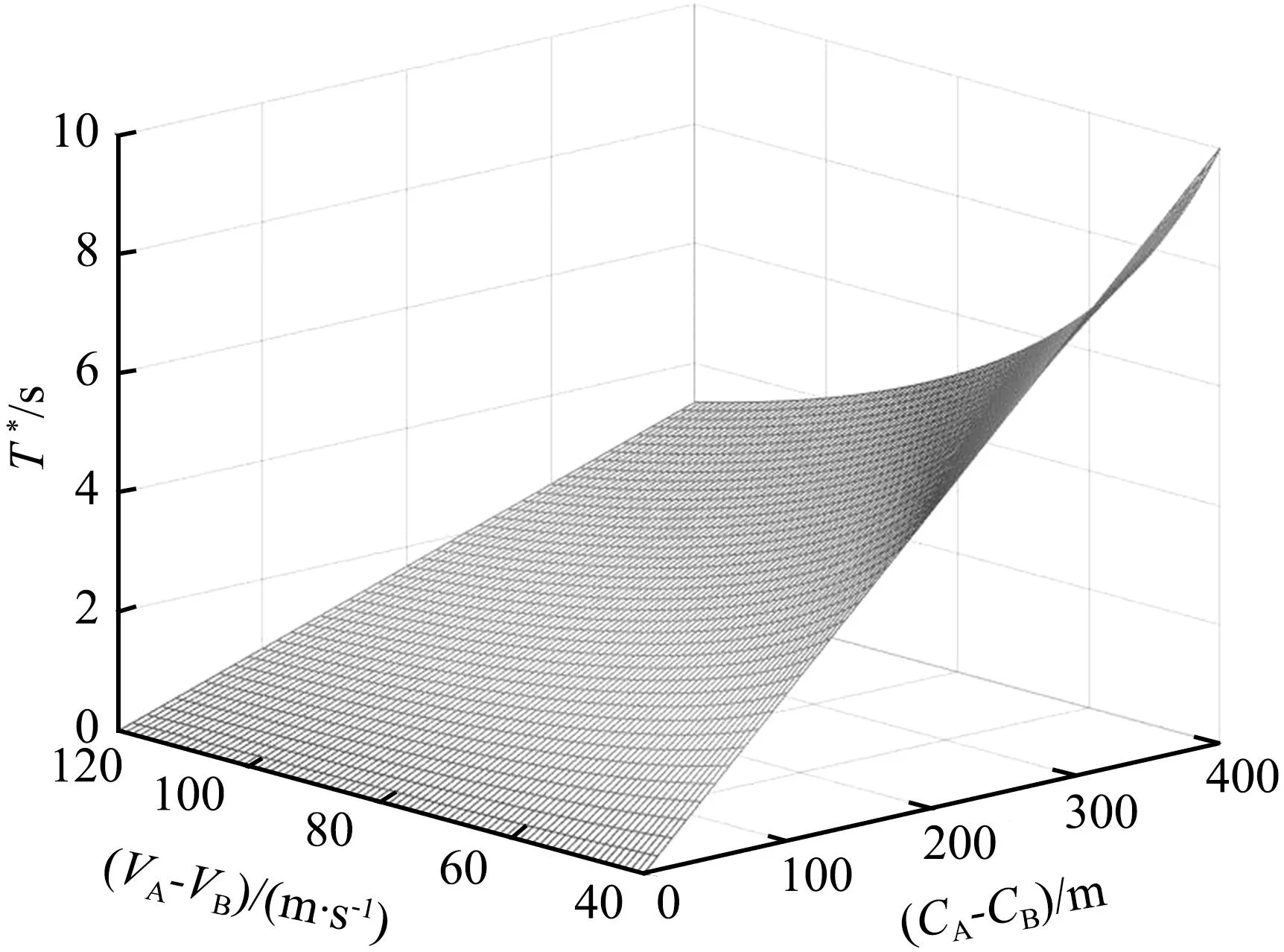
图4 安全阈值T*与速度以及距离关系Fig.4 Relationship among velocity, distance and T*

车联网环境下的自动驾驶车辆在产生换道意图后,获取周围车辆的速度和位置等相关信息。在确定换道车道后,明确博弈对象,开始进入博弈,将换道后的速度增益作为收益函数,然后基于换道博弈的混合策略下的纳什均衡来判断换道之后的收益。之后对换道的安全性及可行性进行分析,即对目标车辆周围的车辆的TTC进行分析,当TTC大于安全阈值6.0 s时,可得换道安全,进行换道;如果小于安全阈值6.0 s时,则相反。目标车辆协作换道的动态博弈过程如图5所示。

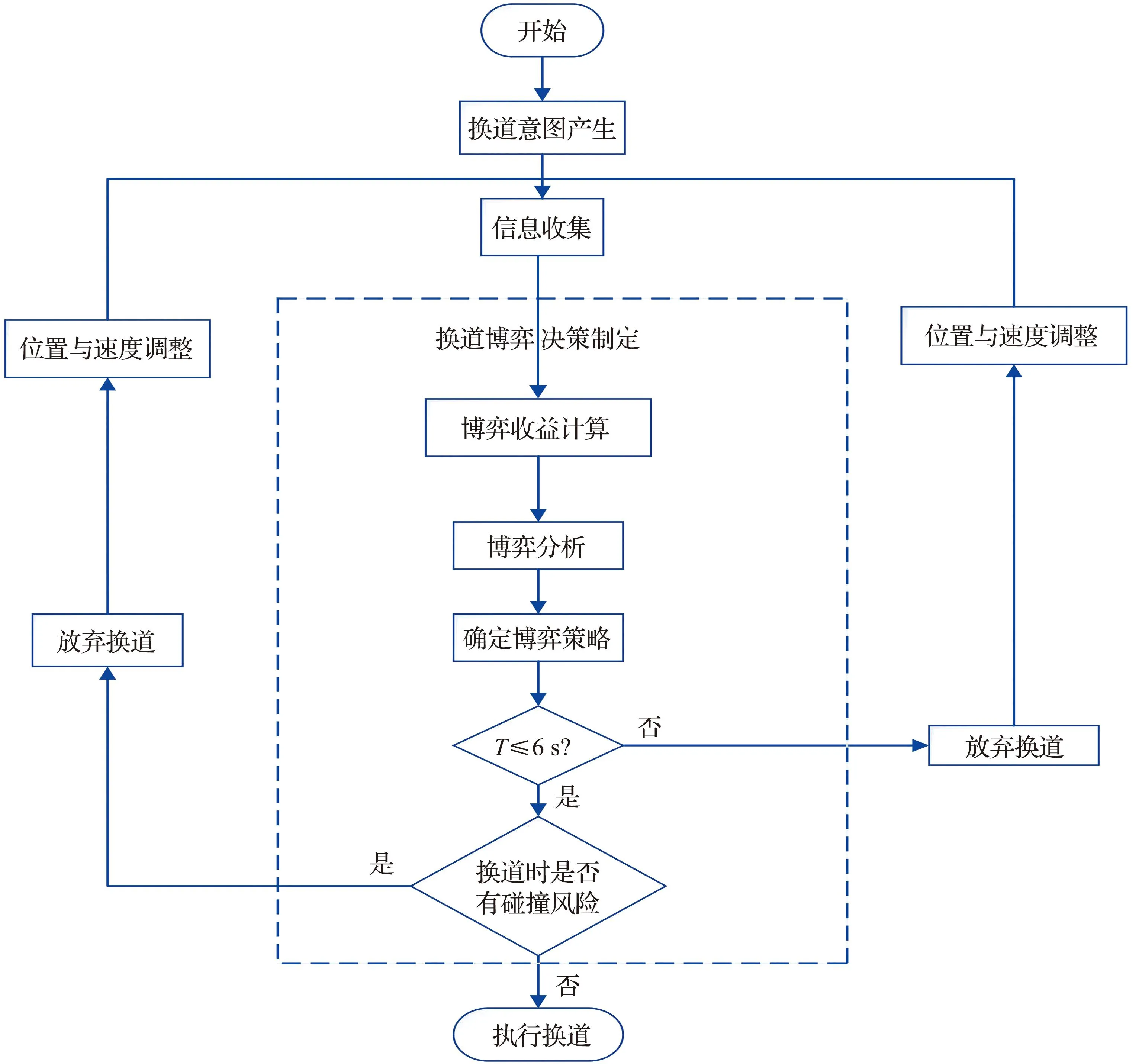
图5 目标车辆协作换道的动态博弈过程Fig.5 Lane change game process

在协作博弈换道行为的模型中,对博弈策略进行分析。目标车辆A的策略集为{t1(换道),t2(不换道)} ;目标车道后车B的策略集为{c1(让道),c2(不让道)}。目标车辆A采取t1策略的概率为p,采取t2策略的概率为1-p;目标车道后车B采取c1策略的概率为q,采取c2策略的概率为1-q。同时将目标车辆换道后所得的速度收益作为博弈所得的收益函数。具体的动态交互博弈矩阵见表4。

表4 动态交互博弈矩阵Tab.4 Dynamic game matrix

目标车辆在4种策略下的速度收益函数分别是uA(t1,c1)、uA(t1,c2)、uA(t2,c1)、uA(t2,c2)。博弈策略中概率变化的同时,速度收益函数也会随之变化,速度收益与博弈策略选择概率的关系如图6所示,在这4种不同概率的策略选择下自动驾驶换道车辆的速度收益分别为-5、-20、-6以及-6。

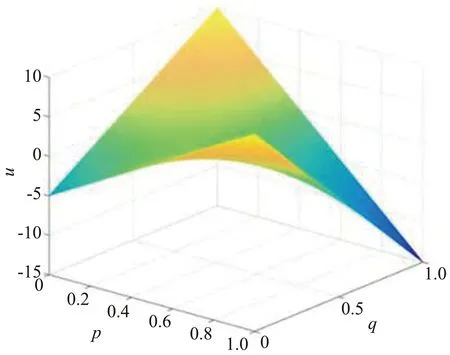
图6 速度收益与博弈策略选择概率的关系Fig.6 Dynamic relationship between speed gain and game strategies

当目标车辆A选择“换道”时,目标车道后车B选择“让道”策略。目标车道后车B进行加速或减速使目标车辆A有足够的空间进入目标车道,即换道成功。因相对车速的变化,两车的TTC阈值也进行了相应的变化。当此混合策略博弈的纳什均衡为目标车辆A选择“换道”时,若目标车道后车B选择“不让道”,为避免发生碰撞事故,博弈决策作废,目标车辆调整相应的速度和位置距离,寻求重新换道的机会。

3 实验结果与分析

3.1 仿真平台

运用SUMO(simulation of urban mobility)软件对协作换道博弈模型的合理性和稳定性进行仿真验证。SUMO是微观和连续交通仿真模拟软件包,可以针对单一目标车辆进行单独的控制。其内置的流量控制接口(traffic control interface, TraCI)可通过Python或者MATLAB软件对其换道规则进行编写。

3.2 仿真环境

为了避免受到目的地、行人以及其他外界环境的影响,本次仿真环境设定为无任何外界因素存在的单向行驶4 000 m三车道,限速为33.3 m/s(即120 km/h)。本次仿真分为1、2两组,1组为使用SUMO内置的换道模型LC2013的对照组,2组为使用本文所给出的协作博弈换道模型。本次仿真所使用的车辆特征参数见表5。

表5 仿真车辆特征参数Tab.5 Simulated vehicle parameters

3.3 仿真结果分析

仿真实验以TTC、不同车流密度下车辆平均速度等来作为评价2组模型好坏的标准。为了对TTC进行具体的分析,对模型中的30辆目标车辆进行定义,使用SUMO的SSM device模块得到目标车辆的TTC,具体数值分布及车辆数如图7所示。根据本文上述所描述的TTC阈值与换道安全风险等级的关系,当T*>6.0 s时,车辆换道处于一个完全安全的状态。在2组模型的对比中,不难看出使用CAV协作换道模型的车辆有更安全的TTC。

图7 不同模型的TTC阈值对比Fig.7 Comparison of TTC Thresholds for Different Models

同时,通过对使用LC2013换道模型和CAV协作换道模型的车辆的一些参数对比来对2组模型的性能进行评估,不同车流密度下的平均速度如图8所示。从图8不难看出,在车流密度小于80 veh/km的情况下,使用CAV协作换道模型的车辆平均速度显然大于使用LC2013换道模型的车辆。在车流密度接近80 veh/km时,2换道模型的车辆平均速度逐渐趋于一致,且都呈现减小的态势。整体仿真效果表明,在不同车流密度下CAV协作换道模型的车辆的平均速度优于LC2013换道模型,即CAV协作换道模型具有更好的工作效率。

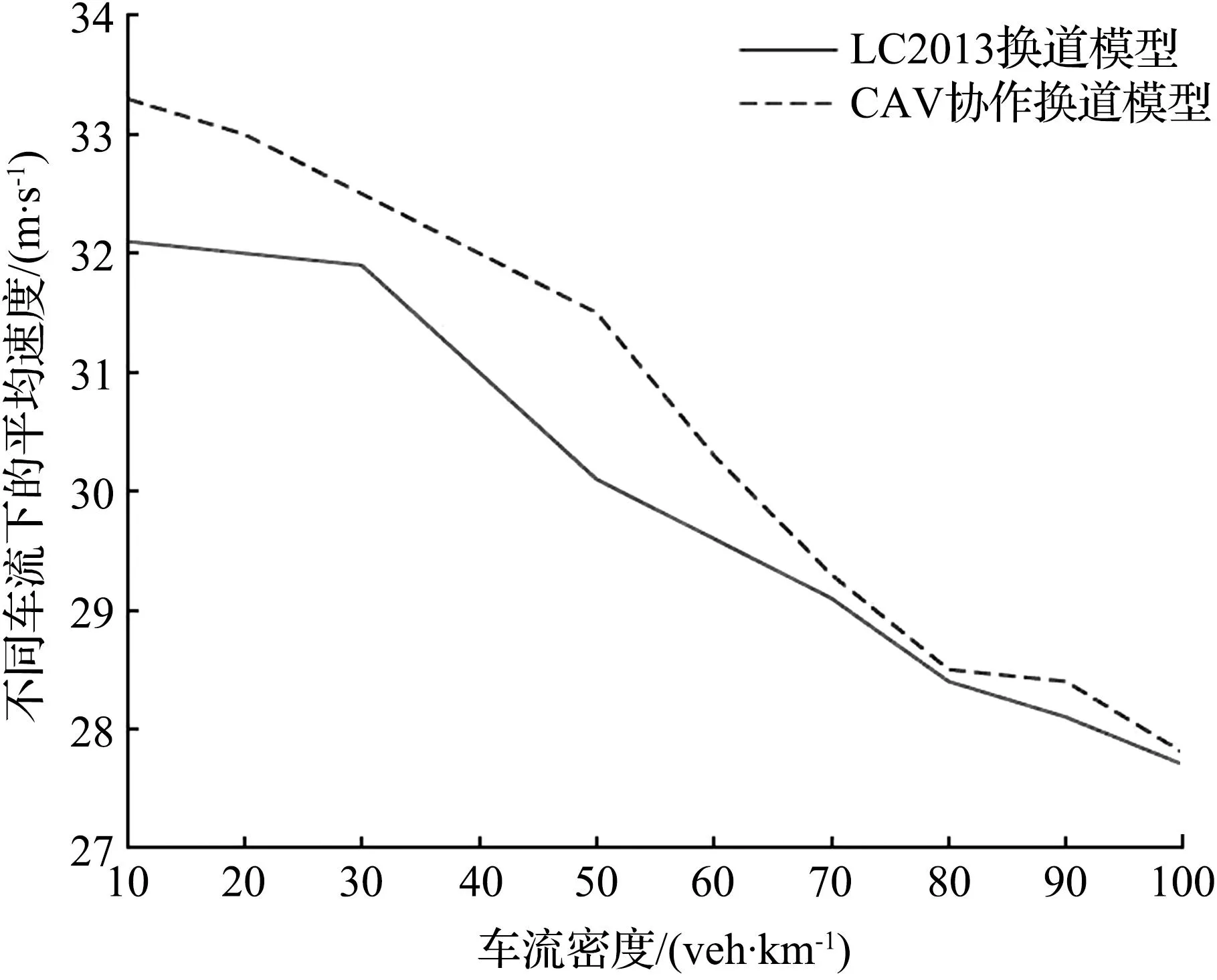
图8 不同车流密度下的平均速度Fig.8 Average velocity in different flow density

不同交通流密度下的车辆通过数如图9所示,对600 s内不同车流密度下的车辆通过数进行比较分析。由图可以看出使用CAV协作换道模型的车流在规定时间内的通过数一直多于使用LC2013换道模型的通过数。这种趋势随着车流密度的上升呈逐步上升的趋势,表明在同一时间路段内、相同车流密度下,本文所研究的CAV协作换道模型与LC2013换道模型相比较车辆通过数更多,即更高效的道路使用率,能够使车辆更加高效的行驶。

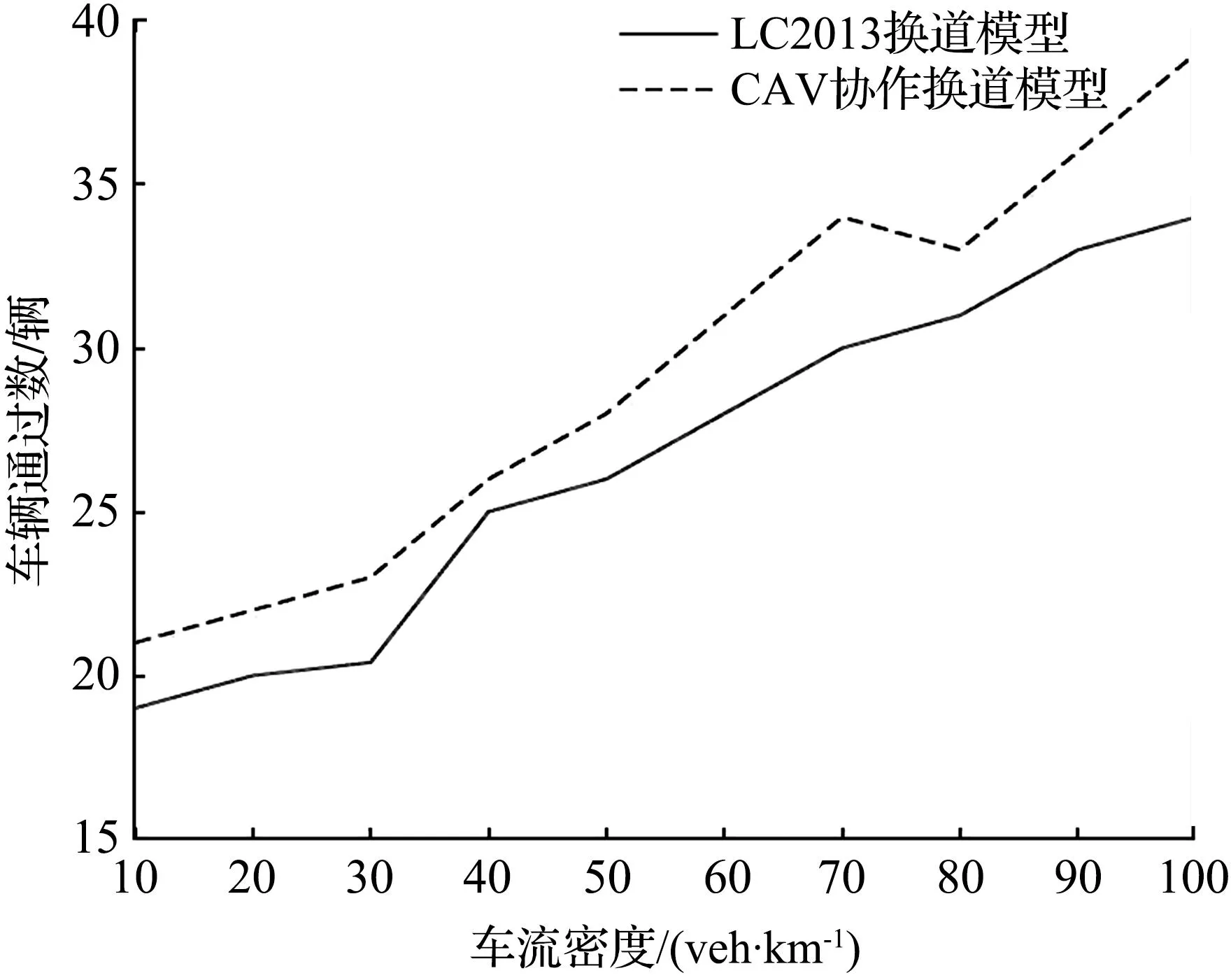
图9 不同交通流密度下的车辆通过数Fig.9 Vehicle count under different traffic flow densities

采取不同换道模型的车辆在相同车流量时发生的事故数如图10所示。从图10中可以看出,在车流密度小于40 veh/km时,LC2013换道模型与CAV协作换道模型都没有事故发生;在车流密度逐渐增大之后,采用LC2013换道模型的车辆事故数开始增加,而采用CAV协作换道模型的车辆处于一个相对安全稳定的状态。综上所述,CAV协作换道模型具有良好的稳定性和安全性。

图10 不同交通流发生的事故数Fig.10 Accident incidents occurring in different traffic flows

4 结语

本文中研究了车联网环境下的异质车群自主车辆动态博弈特性,建立了网联自主车辆协作换道行为模型,运用SUMO和MATLAB软件对其进行了联合仿真及数值分析。研究结果表明,网联异质车群的自主车辆换道存在协作博弈动态关系。基于博弈论量化分析这一协作动态关系,建立了CAV协作换道模型,根据网联自动驾驶目标车辆(CAV)在道路中所处位置,获得交互博弈时间TTC这一动态变量,保证CAV目标车辆的协作博弈行为和安全换道。数值仿真结果表明,CAV协作换道模型比传统LC2013换道模型有更好的收益和稳定性。后续将网联自主车辆协作博弈换道行为,进一步延展人-车-路-环境多维多态的复杂交通场景,深度挖掘网联异质车群的复杂特性。