网联辅助驾驶混合交通流稳定性及安全性分析

秦严严 王 昊 王 炜

(东南大学交通学院, 南京 210096)(东南大学城市智能交通江苏省重点实验室, 南京 210096)(东南大学现代城市交通技术江苏高校协同创新中心, 南京 210096)

网联辅助驾驶系统应用车车无线通信技术能精确感知前车行驶状态,可减少辅助驾驶员驾驶“失误”,改善交通安全等交通流特性[1]．网联辅助驾驶系统设计以及真车实地测试的实施日渐成熟[2-3],在大规模网联辅助驾驶车辆市场普及前,针对常规驾驶车辆与网联辅助驾驶车辆混合交通流特性的研究开展尚不够充分．对网联环境下的各类型自动驾驶汽车混合交通流特性研究较多[4-6]．Talebpour等[7]针对网联辅助驾驶车辆混合交通流,分析了网联辅助驾驶对交通流稳定性的影响,但该研究没有考虑现阶段常规驾驶车辆的车车通信设备安装率较低,紧跟常规车辆的网联辅助驾驶车辆将自然地退化为常规人工驾驶车辆．交通流车辆位置的不确定性造成该退化现象具有较强的随机性,目前鲜有文献考虑这一随机退化现象对网联辅助驾驶混合交通流特性开展研究．鉴于此,本文针对含有随机退化现象的网联辅助驾驶混合交通流进行稳定性分析，并对交通安全特性影响开展研究,为未来大规模网联辅助驾驶背景下的交通流管理与控制提供理论参考．

1 研究对象

1.1 随机退化现象

本文将网联辅助驾驶车辆简称为网联车,交通流稳定性指线性稳定性．在混合交通流中车辆空间分布具有随机性,对于网联车而言,当其前车为网联车时,基于车车通信,网联车可获悉前车行驶状态,起到辅助人工驾驶的作用[8]．然而,在网联车紧跟常规车行驶的情形下,常规车缺乏车车通信设备的固有属性使得网联车无法接收常规车的行车状态．此时,网联车的辅助驾驶系统将无法得到有效应用,网联车则将发生功能退化,转变为常规车,如图1所示．在图中,由网联车退化为常规车的车辆继续保留车车通信系统,使得紧跟其后的网联车不再发生功能退化现象．

图1 网联车退化为常规车

1.2 期望数量比例及验证

假设混合交通流共有N辆车,网联车在退化前的市场率为p,则退化前网联车数量为Np,常规车数量为N(1-p)．网联车退化为常规车的充分必要条件是其前车为常规车,交通流中N足够大,网联车的前车为常规车的概率等于退化前常规车的比例,即1-p．因此,发生退化的网联车数量的数学期望为Np(1-p)，退化后的网联车数量为退化前数量与发生退化的数量之差,即Np-Np(1-p)=Np2,退化后的常规车数量为N-Np2=N(1-p2)．由此可得,退化后的混合交通流中网联车数量比例Pw与常规车数量比例Pc分别为

(1)

式中,下标w和c分别表示网联车和常规车．式(1)描述的是在网联车市场率为p时,混合交通流中实际的网联车与常规车数量比例的数学期望,下面应用随机性仿真实验进行验证．

基于MATLAB软件进行随机性仿真实验,网联车和常规车数量共有300辆,设定网联车市场率为p．基于此,退化现象发生前的网联车与常规车数量由p值随机确定．同时,所有车辆随机分布在单车道道路上．然后根据图1的网联车退化机制,将紧跟常规车的网联车退化为常规车,并统计退化后网联车的数量．考虑到仿真实验中2种车型车辆相对数量、相对位置的随机性,在每个p值时,均重复仿真100次,并计算退化后网联车数量的均值,作为该p值时网联车数量的仿真值．其中p值可由程序从0～1取值,取值间隔为0.01,以此仿真得到不同网联车市场率下的网联车退化情况．

同时,通过式(1)可求得每个p值下,退化后的网联车数量期望解析结果．随机性仿真结果如图2所示．由图2(b)可看出,网联车仿真结果与期望解析结果的绝对误差在3辆车以内,即相对于混合交通流整体数量控制在1%以内,验证了式(1)期望解析表达式的正确性．此外,100辆车的仿真实验表明,仿真结果与解析结果绝对误差在2.5%以内,500辆车的仿真结果与解析结果绝对误差在0.6%以内,表明了车辆总体数量越大,误差将越小．

2 混合交通流稳定性分析

2.1 分析方法

文献[9]推导得到了如下混合交通流稳定性的一般性判别条件:

(a) 网联车数量仿真结果

(b) 仿真结果与解析结果绝对误差

(2)

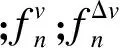
(3)

式中,ve为平衡态速度;se为平衡态车间距．

假设混合交通流中共有N辆车,将式(1)代入式(2),可推广得到如下网联车混合交通流稳定需满足的判别条件:

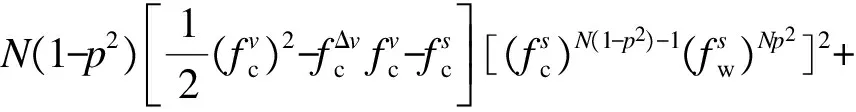
(4)

式(4)可进一步化简为

(5)

式(5)的网联车混合交通流可在p=0和p=1时分别转变为常规车与网联车跟驰模型稳定需满足的判别条件,即

(6)

式中,fc与fw分别表示常规车和网联车跟驰模型稳定性判别条件．

为建立网联车混合交通流稳定性一般性分析框架,令

(7)

F=(Fw-Fc)p2+Fc≥0

(8)

由式(8)可知,网联车与常规车混合交通流稳定性判别条件是关于网联车市场率p平方项的线性函数．因此,当线性函数F≥0时,混合交通流稳定,反之,不稳定．根据线性函数性质,当p2=0时,F=Fc;当p2=1时,F=Fw．

对比式(6)和式(7),可得

(9)

由式(9)可知,当常规车稳定时,Fc≥0,反之,Fc<0;当网联车稳定时,Fw≥0,反之,Fw<0．因此,根据式(8)的线性函数F的性质,将网联车混合交通流稳定性分析分为如下4种情形：

① 常规车稳定、网联车稳定(情形1)．此时Fc≥0,Fw≥0,由线性函数性质可知,式(8)中F值均大于等于0,即此情形下,网联车混合交通流在任意网联车市场率p时均稳定．

② 常规车不稳定、网联车稳定(情形2)．此时Fc<0,Fw≥0,则线性函数F取值如图3(a)所示,在此情形下,当0≤p≤p*时,F<0,即网联车混合交通流不稳定,p*为交通流变为稳定状态时的网联车市场率．随着网联车市场率p的增加,当p达到p*时,F≥0,即混合交通流变为稳定状态．并且,p*2为函数F与水平轴的交点,容易求得

(10)

③ 常规车稳定、网联车不稳定(情形3)．此时,Fc≥0,Fw<0,则线性函数F如图3(b)所示,因此,当0≤p≤p*时,网联车混合交通流稳定,当p增大到p*时,网联车混合交通流开始变为不稳定,并且此情形下的p*值仍然可通过式(10)计算得到．

④ 常规车不稳定、网联车不稳定(情形4)．此时Fc<0,Fw<0,由线性函数性质可知,此情形下F值均小于0,即网联车混合交通流在任意网联车市场率p时均不稳定．

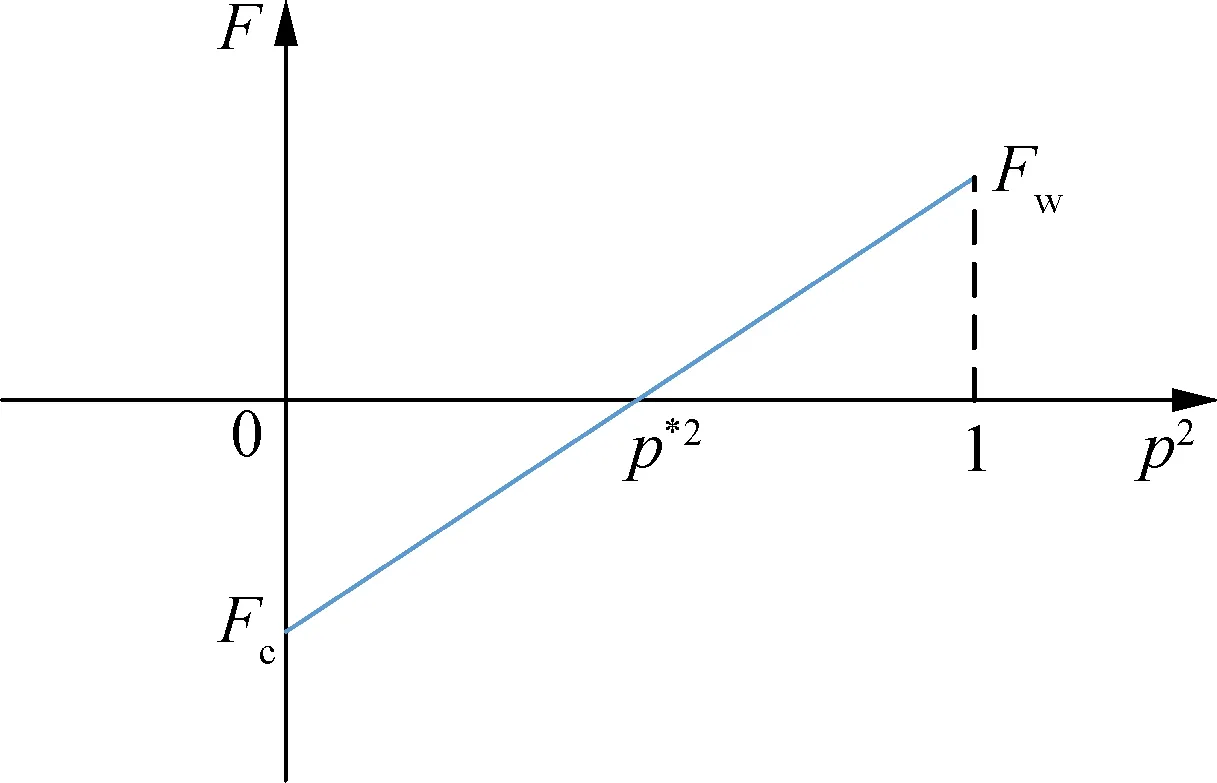
(a) 情形2

(b) 情形3

2.2 案例分析

2.2.1 跟驰模型

全速度差(full velocity difference, FVD)模型[10]可较好反映常规车辆跟驰行为,被广泛应用于常规车辆跟驰模型研究．文献[11]对FVD模型添加车间距项,并应用实测数据进行了模型标定,模型公式如下:

(11)

式中,κ和λ为敏感系数;V(s)为优化速度函数,即

(12)

式中,v0为自由流速度;α为敏感系数;s0为最小停车间距．文献[11]应用车辆轨迹数据对FVD模型进行了参数标定,轨迹数据通过车载GPS以及雷达传感器进行采集,采集地点为法国巴黎,采集时间为上午9:00—10:45,模型参数标定误差为4.02%,标定结果为v0=33.0 m/s,κ=0.629 s-1,λ=4.10 s-1,α=1.26 s-1,s0=2.46 m．

对于网联车而言,智能驾驶员模型(intelligent driver model, IDM)[12]可有效反映常规驾驶员在精确获悉前车行驶状态时的“智能”驾驶特性．因此,网联车跟驰模型选择IDM模型,模型公式如下:

(13)

式中,a为最大加速度;T为安全车头时距;b为舒适减速度．依据文献[7],网联车跟驰特性模型的参数取值为v0=33.0 m/s,T=2.0 s,s0=2.0 m,a=4.0 m/s2,b=2.0 m/s2．

2.2.2 稳定性分析结果

将常规车以及网联车跟驰模型式(11)与式(13)分别代入式(3),计算得到

(14)

(15)

将式(14)和式(15)代入式(6),并将跟驰模型参数同时代入,计算得到常规车稳定性条件fc和网联车稳定性条件fw下的平衡态速度,如图4所示．由图可知,常规车在2.9～21.1 m/s速度范围内不稳定,其他速度范围稳定．网联车在0～33 m/s 的自由流速度范围内均稳定．

根据上述常规车与网联车稳定性情况,按照2.1节给出的网联车混合交通流稳定性一般性分析的4种情形,本文选取常规车与网联车跟驰模型的情形1和情形2进行如下分析:

① 情形1下平衡态速度范围为0～2.9 m/s和21.1～33.0 m/s,在这2个速度范围内,常规车和网联车均稳定,所以网联车混合交通流在任意网联车市场率下均稳定．

② 情形2对应平衡态速度范围为2.9～21.1 m/s,常规车不稳定,网联车稳定．将式(9)、(14)、(15)代入式(10),计算得到各平衡态速度对应的p*值,使得当网联车市场率p增大到p*时,网联车混合交通流由不稳定转变为稳定．

(a) 常规车稳定性

(b) 网联车稳定性

综合情形1和情形2,根据式(8)计算不同平衡态速度v、不同网联车市场率p的网联车混合交通流稳定性条件F值,得到网联车混合交通流稳定域,如图5所示．在图中,曲线为情形2中各平衡态速度下的p*值,曲线下方区域为混合交通流不稳定区域,曲线上方区域为混合交通流稳定区域．曲线在p=0时与速度轴的交点为常规车稳定的速度临界值,即分别为2.9和21.1 m/s．当速度低于2.9 m/s或高于21.1 m/s时,网联车混合交通流在任意网联车市场率下均稳定．同时计算得到各平衡态速度下p*值的最大值为0.37,对应的平衡态速度范围为9.8～10.6 m/s.平衡态速度越接近9.8～10.6 m/s,混合交通流满足稳定状态所需的

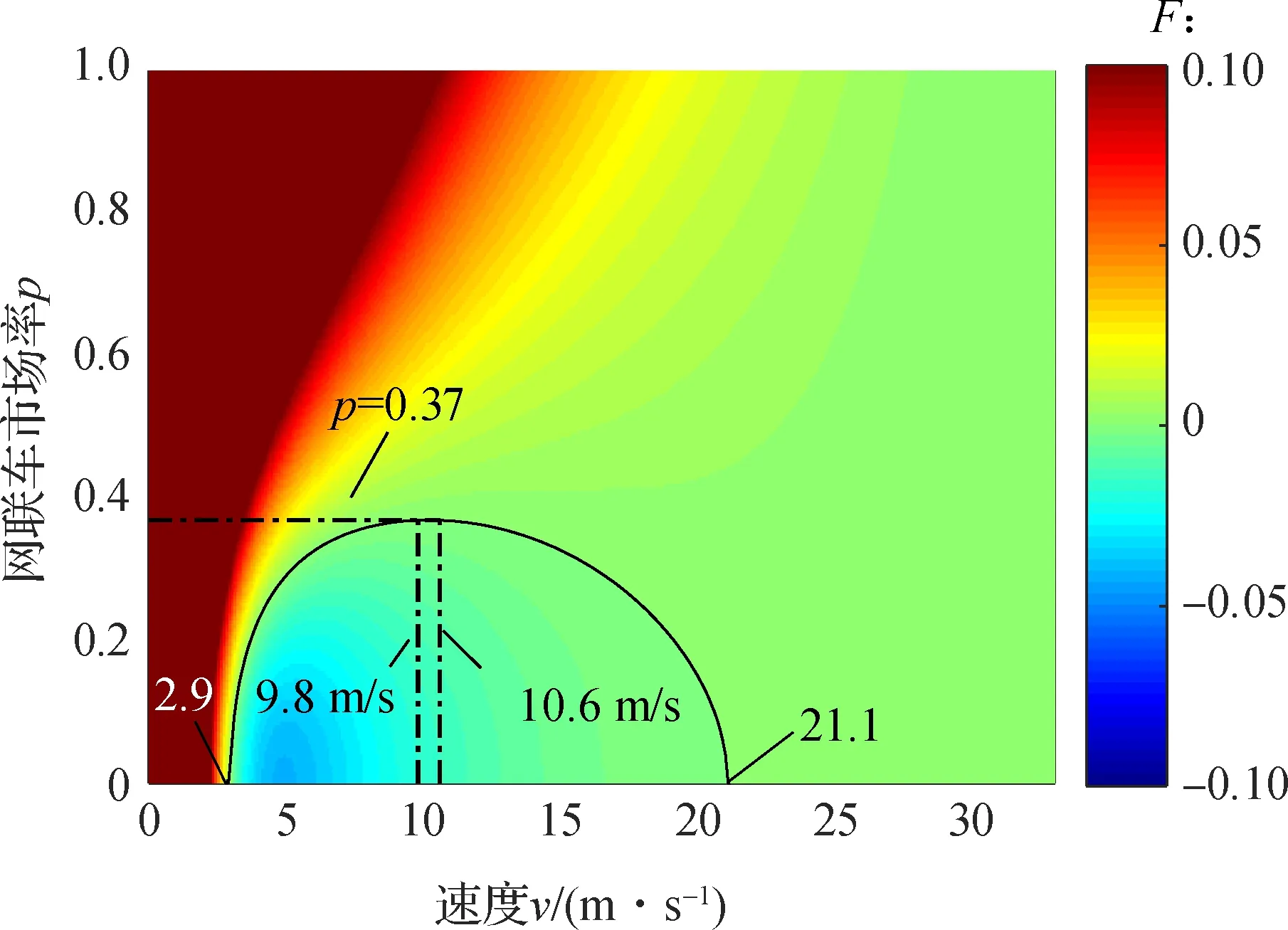
图5 混合交通流稳定域

网联车市场率临界值p*越大,当网联车市场率大于0.37时,混合交通流可在任意平衡态速度下稳定．

3 交通流安全性分析

3.1 评价指标

应用文献[13]提出的TET指标和TIT指标进行交通流车辆尾部碰撞交通安全隐患评价．指标计算公式如下:

(16)

(17)

式中,i为仿真中车辆编号;I为仿真中车辆总数;j为仿真时刻;J为仿真时间离散化后的时间总量;τ为跟驰模型仿真步长;T*为阈值．

3.2 仿真实验与结果

依据文献[7],上匝道瓶颈的数值仿真实验中主路和匝道均为单车道路段,路段总体长度为6.5 km,匝道区位于整个路段中间位置．主路和匝道需求选取高需求和低需求2组.高需求情况下,主路上游需求为1 800 veh/h,匝道需求为360 veh/h;低需求情况下,主路上游需求为1 200 veh/h,匝道需求为200 veh/h,仿真步长为0.1 s,仿真时间为1 h．

在仿真实验中,若网联车前车为常规车,则退化为常规车．考虑仿真中的随机性,在各网联车市场率下,均重复仿真5次,并对仿真结果取均值作为该网联车市场率的安全性仿真结果,并对TET和TIT指标中的阈值T*在1～3 s内进行参数敏感性分析．以p=0时的TET和TIT指标仿真结果为基准,计算各网联车市场率下影响安全指标TET和TIT的提高百分数,分别如表1～表4所示．

基于仿真结果可以看出,阈值T*取值大小并不影响网联车市场率对混合交通流安全特性的影响,且主路和匝道的不同需求亦不影响网联车对交通安全水平的提升作用．随着p的增加,交通安全水平逐步提高,但当p<0.3时,交通安全水平提高较小,TET和TIT提高百分数小于11.92%;当p>1时,交通安全水平TET和TIT均可提高54.29%～71.36%．

表1 高需求情况下TET提高百分数(相对于p=0) %

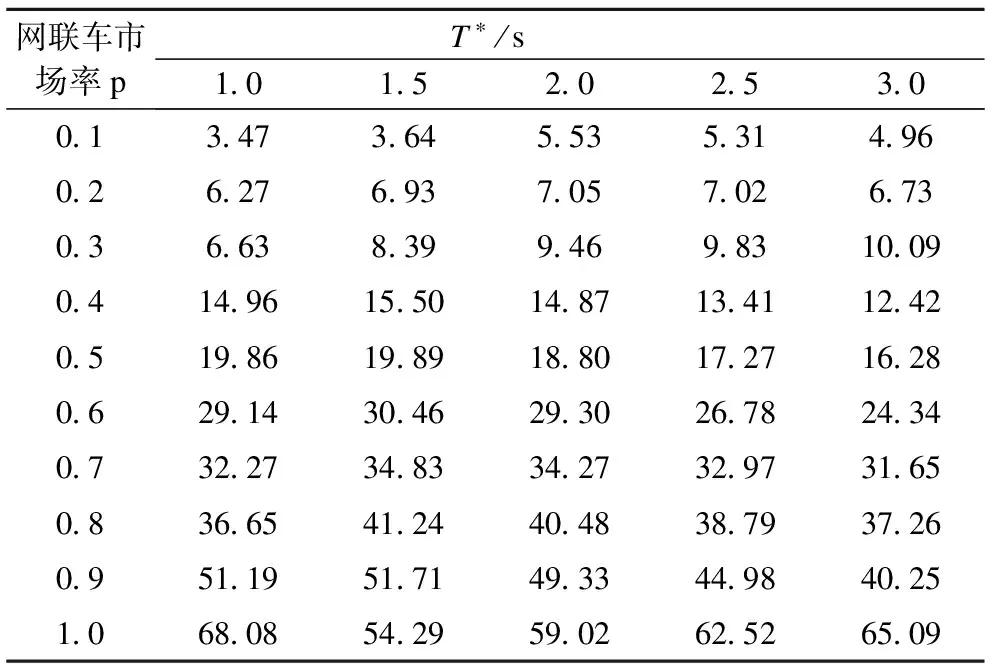
表2 高需求情况下TIT提高百分数(相对于p=0) %

表3 低需求情况下TET提高百分数(相对于p=0) %

表4 低需求情况下TIT提高百分数(相对于p=0) %

4 结论

1) 针对紧跟常规车的网联车退化为常规车的随机退化情形,建立了各车型车辆相对数量比例的数学期望表达式,建立了网联车混合交通流稳定性的一般性分析方法,将网联车混合交通流稳定性分为4种一般性情形,并给出了一般性的稳定性判别条件．

2) 基于选取的常规车与网联车跟驰模型,得到关于网联车市场率与平衡态速度的混合交通流稳定域.结果表明,当速度低于2.9 m/s或高于21.1 m/s时,网联车混合交通流在任意网联车市场率下均稳定;平衡态速度越接近9.8～10.6 m/s的速度范围,混合交通流满足稳定状态所需的网联车市场率临界值越大,当网联车市场率大于0.37时,混合交通流可在任意平衡态速度下稳定．基于常规车与网联车跟驰模型的上匝道瓶颈交通安全仿真结果表明,网联车有利于提升交通安全,但当网联车市场率低于0.3时,交通安全水平提升小于11.92%,而网联车交通流相比于常规车交通流,交通安全水平可提高54.29%～71.36%．

3) 建立的网联车混合交通流稳定性解析具备一般性意义,能够适用于不同常规车以及网联车跟驰模型的选取,可为未来大规模网联车背景下的交通流管理与控制提供理论参考．

4) 随着我国网联车实地测试的逐步开展,基于实测数据提出并标定符合我国交通流特性的网联车跟驰模型,分析其对我国传统交通流稳定性以及交通安全的影响是下一步的研究方向．

)

[1] Mahmassani H S. 50th anniversary invited article—Autonomous vehicles and connected vehicle systems:Flow and operations considerations[J].TransportationScience, 2016,50(4): 1140-1162. DOI:10.1287/trsc.2016.0712.

[2] 郭孜政, 潘毅润, 潘雨帆, 等. 基于EEG熵值的驾驶员脑力负荷水平识别方法[J]. 东南大学学报(自然科学版), 2015, 45(5): 980-984. DOI: 10.3969/j.issn.1001-0505.2015.05.028.

Guo Zizheng, Pan Yirun, Pan Yufan, et al. Recognition method of driving mental workload based on EEG entropy[J].JournalofSoutheastUniversity(NaturalScienceEdition), 2015,45(5): 980-984. DOI: 10.3969/j.issn.1001-0505.2015.05.028. (in Chinese)

[3] Liu H, Wei H, Zuo T, et al. Fine-tuning ADAS algorithm parameters for optimizing traffic safety and mobility in connected vehicle environment[J].TransportationResearchPartC:EmergingTechnologies, 2017,76: 132-149. DOI:10.1016/j.trc.2017.01.003.

[4] Shladover S E, Nowakowski C, Lu X Y, et al. Cooperative adaptive cruise control: Definitions and operating concepts[J].TransportationResearchRecord:JournaloftheTransportationResearchBoard, 2015,2489: 145-152.

[5] Chen D, Ahn S, Chitturi M, et al. Towards vehicle automation: Roadway capacity formulation for traffic mixed with regular and automated vehicles[J].TransportationResearchPartB:Methodological, 2017,100: 196-221. DOI:10.1016/j.trb.2017.01.017.

[6] 秦严严, 王昊, 王炜, 等. 自适应巡航控制车辆跟驰模型综述[J]. 交通运输工程学报, 2017, 17(3): 121-130. DOI:10.3969/j.issn.1671-1637.2017.03.013.

Qin Yanyan, Wang Hao, Wang Wei, et al. Review of car-following models of adaptive cruise control[J].JournalofTrafficandTransportationEngineering, 2017,17(3): 121-130. DOI:10.3969/j.issn.1671-1637.2017.03.013.(in Chinese)

[7] Talebpour A, Mahmassani H S. Influence of connected and autonomous vehicles on traffic flow stability and throughput[J].TransportationResearchPartC:EmergingTechnologies, 2016,71: 143-163. DOI:10.1016/j.trc.2016.07.007.

[8] Wang J Q, Xiong C F, Lu M, et al. Longitudinal driving behaviour on different roadway categories: An instrumented-vehicle experiment, data collection and case study in China[J].IETIntelligentTransportSystems, 2015,9(5): 555-563. DOI:10.1049/iet-its.2014.0157.

[9] Ward J A. Heterogeneity, lane-changing and instability in traffic: a mathematical approach[D]. Bristol, UK: University of Bristol, 2009.

[10] Jiang R, Wu Q, Zhu Z. Full velocity difference model for a car-following theory[J].PhysicalReviewE, 2001,64(1): 017101. DOI:10.1103/PhysRevE.64.017101.

[11] Wang H, Wang W, Chen J, et al. Estimating equilibrium speed-spacing relationship from dynamic trajectory data[C]//TransportationResearchBoard91stAnnualMeeting. Washington, DC, USA, 2012: 1-18.

[12] Treiber M, Hennecke A, Helbing D. Congested traffic states in empirical observations and microscopic simulations[J].PhysicalReviewE, 2000,62(2): 1805-1824. DOI:10.1103/physreve.62.1805.

[13] Minderhoud M M, Bovy P H L. Extended time-to-collision measures for road traffic safety assessment[J].AccidentAnalysis&Prevention, 2001,33(1): 89-97. DOI:10.1016/s0001-4575(00)00019-1.