大直径嵌岩桩桩端极限承载力计算方法

张 琦 刘 军 戴国亮 龚维明

(东南大学混凝土及预应力混凝土结构教育部重点实验室, 南京 210096)(东南大学土木工程学院, 南京 210096)

随着我国公路、铁路事业的快速发展,以及(超)高层的涌现,建(构)筑物的基础承担的荷载越来越大.大直径(d=0.8m)嵌岩桩因其具有单桩承载力高、沉降变形小、沉降收敛快、抗震性能好等诸多优点,在工程界的应用越来越广泛[1].但目前对于嵌岩桩的荷载传递、承载性状、破坏机理等存在着不同的认识,现行各部门、各行业的规范在嵌岩桩承载力的计算方法上差异较大.

嵌岩桩的承载力通常由桩土和桩岩界面的摩阻力及桩端阻力组成.目前,规范中的计算方法从工程安全、施工质量等角度考虑,桩端岩石的极限承载力分项系数较低,设计中存在较大的安全储备,甚至在部分规范中不予考虑,而过大的承载力富余显然极不利于工程的经济性.

为进一步研究大直径嵌岩桩的承载性状,充分合理并更加准确地评价桩端岩体的极限承载力,本文假定大直径嵌岩桩桩端岩体破坏存在的3种极限状态:桩端岩体整体连续滑裂破坏、桩周岩体剪切破坏、桩周岩体微裂纹断裂破坏.基于岩体二维、三维Hoek-Brown(H-B)破坏准则、岩体微裂纹Ⅰ-Ⅱ型复合判据,提出4种大直径嵌岩桩桩端岩体极限承载力的计算方法.利用文献[2]实测数据对所提出的计算方法进行对比分析和验证,进一步研究了大直径嵌岩桩的尺寸效应,揭示了嵌岩深度和桩径对桩端岩体极限承载力的影响.

1 现行桩端承载力确定方法

现行计算桩端极限承载力的方法分为两大类:

1) 第1类.桩端极限承载力计算式为

qmax=Nσσc

(1)

式中,qmax为桩端极限荷载(单位面积极限承载力);Nσ为桩端阻力系数;σc为岩石单轴抗压强度,MPa.

该方法被现行的多个规范所广泛采用,如美国公路与运输协会标准(AASHTO)根据岩石质量和岩石分类给出相应的Nσ,对于质量非常好的岩石,依据5种岩石分类分别给出Nσ为1.4,1.6,1.9,2.0和2.3.中国《建筑桩基技术规范》(JGJ 94—2008)根据嵌岩比、成桩工艺等可确定嵌岩段的桩端阻力系数,对于极软岩和软岩、较硬岩和坚硬岩,Nσ的取值见表1[3].

2) 第2类.桩端极限承载力计算式为

(2)

Zhang等[4]通过对大量实测数据的统计,给出了经验系数Nσ的取值区间为3.0～6.6.

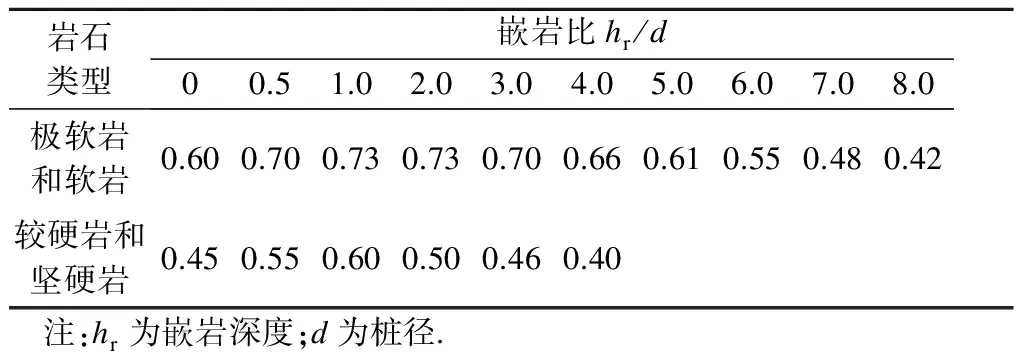
表1 桩端阻力系数Nσ

式(1)和(2)桩端岩体极限承载力的计算方法均是通过岩石单轴抗压强度经简单换算得到,而实际工况中桩端的岩体同时受到桩身荷载和围压的共同作用,处于三向受压的应力状态,因此导致得到的桩端岩体极限承载力设计值较为保守.此外,现行方法受人为因素影响较大,过多地依靠经验统计,极限端阻力系数取值区间很大,可能导致最终计算得到的承载力与实际值差异较大.

2 桩端岩体极限承载力计算方法

2.1 二维H-B准则的桩端整体滑裂破坏解法

嵌岩桩桩底基岩在极限荷载qmax的作用下,当嵌岩比较小时,桩端岩体破坏模式为连续滑动整体破坏,在桩底岩体产生滑动楔体.Zhang等[4]提出基于二维H-B准则并考虑桩端面以上岩土层自重影响的嵌岩桩桩端岩体极限承载力计算方法.该方法所采用的强度极限破坏条件H-B准则的表达式如下[5]:

(3)

式中,σ1,σ3为最大、最小主应力;mb,s,a为反映岩体特征的经验参数,其中,mb为针对不同岩体的无量纲经验参数,s反映岩体破碎程度,取值范围为0～1.0,对于完整岩体(即岩石),s=1.0.Hoek等[6]基于地质强度指标(GSI)提出mb,s,a的取值方法,即

(4)

式中,mi为反映岩石软硬程度的参数,可以通过查表获得[7];D为反映爆破影响和应力释放引起扰动程度的参数,取值范围为0～1.0,现场无扰动岩体为0,而非常扰动岩体为1.0.

基于二维H-B准则和桩端岩体产生整体连续滑裂面的破坏模式如图1所示.其中,hs为上覆土的高度;qs为上覆岩土层自重;σ3A,σ1B分别为楔体A、楔体B的最小主应力和最大主应力.

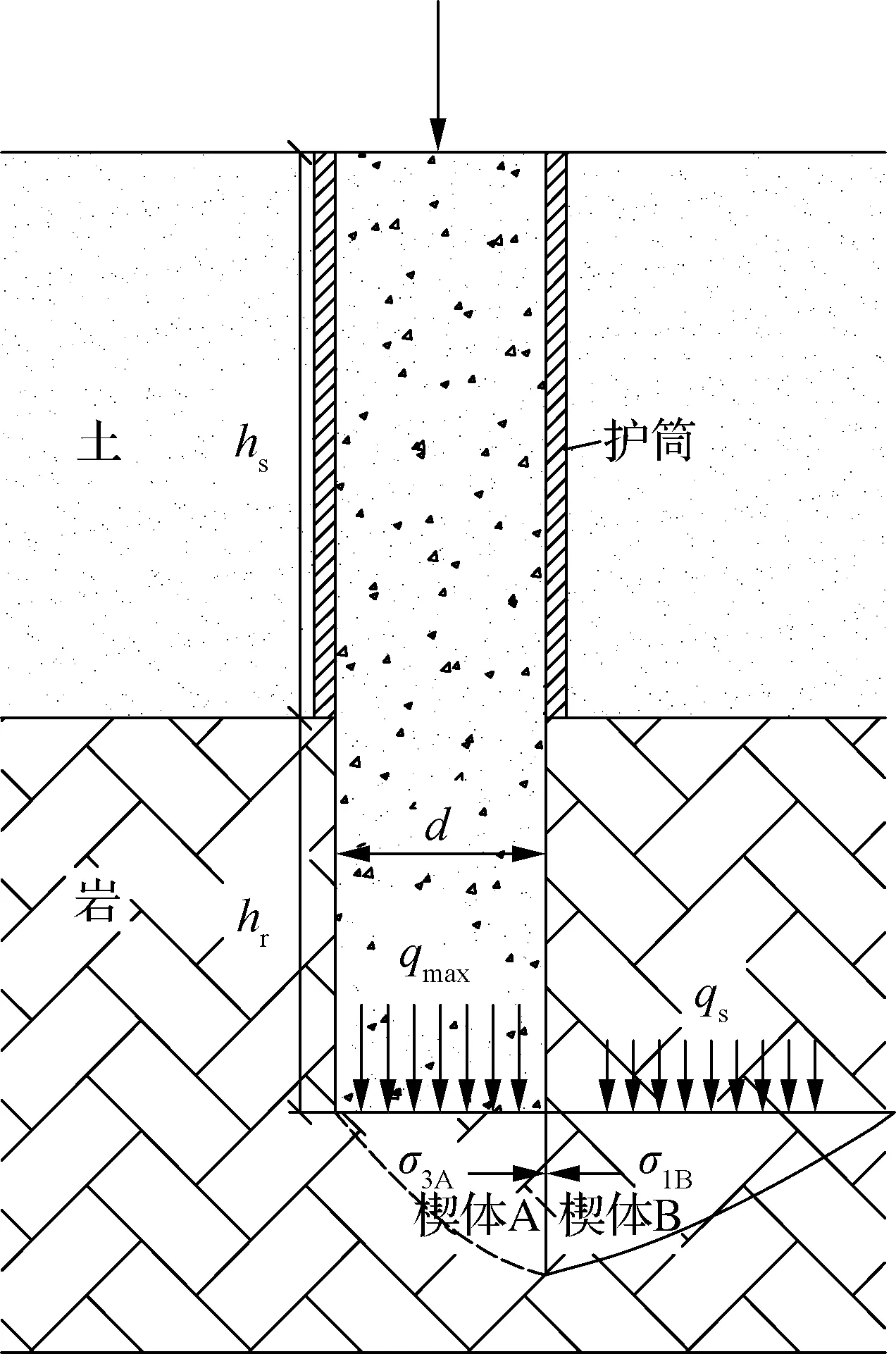
图1 桩端岩体的整体滑动破坏模式[4]

桩端岩体简化为二维平面应变条件,根据整体滑动破坏过程分析可得，楔体B处于被动应力状态,因此最小主应力为上覆岩土层自重qs.当楔体B达到极限状态时,其最大主应力σ1B为水平方向,且满足式(3),即

(5)

而楔体A处于主动应力状态,桩底压力qmax为最大主应力,最小主应力σ3A为水平方向,达到极限状态时,其最大主应力和最小主应力满足式(3),即

(6)

而楔体A与楔体B是相互直接连接的,满足如下边界连续条件:

σ3A=σ1B

(7)

桩端岩体的极限荷载为

(8)

基于连续滑裂面和二维H-B准则的计算方法没有考虑中主应力σ2的影响,而在实际中桩端岩体处于三向受压的应力状态,其强度会有所增加.因此,基于连续滑裂面和二维H-B准则的计算方法还是偏于保守,但与现行规范中采用的通过岩石饱和单轴抗压强度经换算而得到的桩端岩体极限承载力计算方法相比更为合理.

2.2 二维H-B准则的桩周岩体剪切破坏解法

李镜培等[8]依据滑移线场的叠加,获得桩基础破坏的规律.当上覆岩层较薄时,基础边缘处先屈服,其宏观表现为桩周剪切破坏,因此当不考虑上覆岩层的影响且基岩为硬岩时,一般嵌岩桩入岩层深度都较小,故可认为桩周岩层先发生破坏.基于二维H-B准则和桩周剪切破坏的极限承载力计算方法,采用在各向同性半无限空间体的表面下某一深度处在垂直集中力影响下的应力场和位移场的理论解.

当桩体埋深为hr时,桩端周边缘处任一点的应力分量的Mindlin解析解为

(9)

(10)

(11)

τyz=τxy=0

(12)

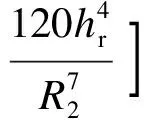
(13)

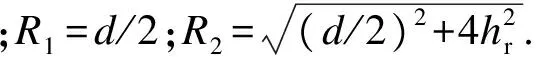
根据空间一点应力状态的6个独立分量与主应力及主方向的解析关系式[9],可得桩端周边缘处任意一点的3个主应力σ1,σ2,σ3.忽略σ2的影响,将σ1和σ3代入式(3)即可直接计算出基于二维H-B准则的桩周岩体剪切破坏极限承载力P.

2.3 三维H-B准则的桩周岩体剪切破坏解法

大量的岩体试验研究表明,中主应力σ2对岩体强度存在影响.在分析大直径嵌岩桩桩端岩体的极限承载力时,如能考虑中主应力σ2将更加合理,前面2种计算方法均未考虑σ2的影响.Zhang等[10]基于H-B准则和Mogi准则,提出了真三维H-B准则,该准则的表达式为

(14)

式中,σm,2和τoct分别为最大与最小主应力的平均值和八面体剪应力,表达式如下:

(15)

(16)

Zhang[11]进一步完善该三维准则,进行了适用于岩体的扩展,提出了广义三维H-B岩体强度准则,其表达式为

(17)

同样,根据空间一点的应力状态的6个分量与主应力及主方向的解析关系式,可得桩端周边缘处任意一点的3个主应力σ1,σ2,σ3,将其代入式(17)即可直接求解出基于三维H-B准则的桩周岩体剪切破坏极限承载力P.

2.4 Ⅰ-Ⅱ 型复合判据的桩周岩体微裂纹断裂解法

天然岩体是地质历史时期的产物,因此含有大量随机分布的裂隙和结构面,而作为工程地基的岩体,这些裂隙和结构面在工程荷载作用下,可能扩展成新的破坏(断裂)[12].潘别桐等[13]基于最大周向拉应力理论提出适用于岩石压剪断裂的Ⅰ-Ⅱ型复合断裂判据,该判据可以考虑岩体内的裂隙在压应力的作用下闭合而产生的摩擦效应,较适用于嵌岩桩桩端岩体的三向受压的应力状态.

桩端边缘处任意一点的3个主应力σ1,σ2,σ3计算同上.在最普遍的情况下,工程岩体中的断裂面可以是空间曲面,断裂前缘可以是空间曲线,但为计算简单起见,同时考虑到在实际工程中常遇见的是平面断裂或可按平面断裂处理[12],同时假定在桩周附近很小范围内的应力变化不大,则可忽略中主应力σ2的影响按平面问题考虑.桩端边缘岩体内的某一裂隙的应力状态如图2所示.

将应力坐标进行变换,得

(18)

式中,β为岩体中天然裂隙与σ1之间的夹角,rad.

Ⅰ-Ⅱ 型复合断裂的起裂角θ0可由下式确定[14]:

KⅠsinθ0+KⅡ(3cosθ0-1)=0

(19)

式中,KⅠ,KⅡ分别为Ⅰ型、Ⅱ型应力强度因子,MPa·m1/2,当σy<0时,裂纹壁面无摩擦效应,KⅠ,

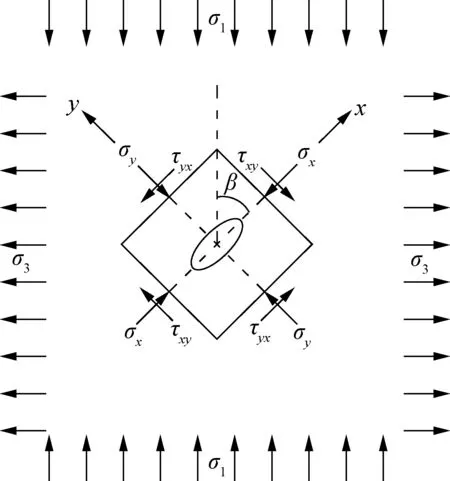
图2 Ⅰ-Ⅱ型复合断裂应力图[13]

KⅡ由下式计算[14]：

(20)

当σy>0时,需考虑裂纹壁面的摩擦效应,KⅠ,KⅡ由下式计算[13]:

(21)

式中,r为天然裂隙的裂隙半长,m;μ为裂隙壁面间的摩擦系数.

由于材料在压缩荷载的作用下不产生张开断裂,式(20)和(21)中的Ⅰ型应力强度因子KI为负值,表示引起裂纹闭合[15].将式(20)和(21)代入式(19),可得

(22)

(23)

式中,β为自变量,θ0为因变量,由式(22)或式(23)得到θ0.当σy<0时,无裂纹壁面的摩擦效应,则岩石拉剪状态下Ⅰ-Ⅱ型复合断裂判据(即最大周向拉应力理论)为[14]

(24)

当σy>0时,考虑裂纹壁面摩擦效应的岩石压剪状态下Ⅰ-Ⅱ型复合断裂判据为[13]

4KⅠc

(25)

式中,KⅠc为Ⅰ型应力强度因子临界值,MPa·m1/2,为材料的断裂韧度.

岩石类材料的抗拉强度与Ⅰ型断裂韧度之间存在较好的线性相关关系.Zhang[16]通过统计不同类型岩石的Ⅰ型断裂韧度和抗拉强度的试验数据,得到两者之间的相关关系,即

σt=6.88KⅠc

(26)

式中,σt为岩石的单轴抗拉强度,MPa.

文献[17]建立了如下反映不同类型岩石软硬程度的H-B准则经验参数mi、岩石拉伸强度σt、单轴抗压强度σc的经验关系式:

(27)

由式(26)和式(27)可知,只需已知岩石单轴抗压强度σc和岩石经验参数mi,即可得到岩石的Ⅰ型断裂韧度KⅠc.联立式(18)～(27),可求解出基于Ⅰ-Ⅱ型复合判据的桩周岩体微裂纹发生断裂时的大直径嵌岩桩桩端极限荷载以及极限承载力.

3 桩端极限承载力计算方法对比与验证

为了检验本文中提出的各计算方法的准确性,参照文献[2]中的桩端极限承载6组试验数据,采用2种现行方法和本文所提出的4种计算方法分别计算桩端极限承载力.桩径d=1.064 m，岩石重度γr=16.3 kN/m3，其余参数见表2.

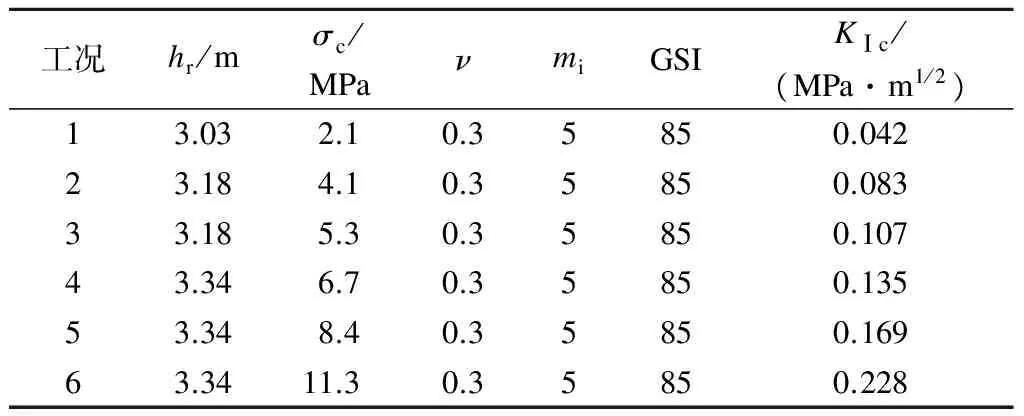
表2 试验参数[2]

桩基为结构致密、孔隙率低的石膏岩,计算中取裂隙半长r=1 mm[18],取裂隙壁面的摩擦系数μ=0.32.由于天然岩体中裂隙的分布具有随机性,角度β∈(-π/2,π/2],β分布对岩体强度有重要的影响.本文采用近似计算方法,将β假定为-π/3,-π/4,-π/6,0,π/6,π/4,π/3,π/2,最终的桩端岩体极限承载力取该8种情况下所求解结果的最小值.

采用第1节中的2种现行方法和本文所提出的4种计算方法进行桩端岩体的极限承载力qmax的计算,计算结果如图3所示.其中,方法1为《建筑桩基技术规范》(JGJ 94—2008),即式(1)计算结果;方法2为式(2)取中间值,即qmax=4.8σc0.5计算结果;方法3为基于二维H-B准则的桩端整体滑裂破坏的桩端极限荷载计算结果;方法4为基于二维H-B准则的桩周岩体剪切破坏的桩端极限荷载计算结果;方法5为基于三维H-B准则的桩周岩体剪切破坏的桩端极限荷载计算结果;方法6为基于Ⅰ-Ⅱ型复合判据的桩周岩体微裂纹断裂的桩端极限荷载计算结果;方法7为实测数据.

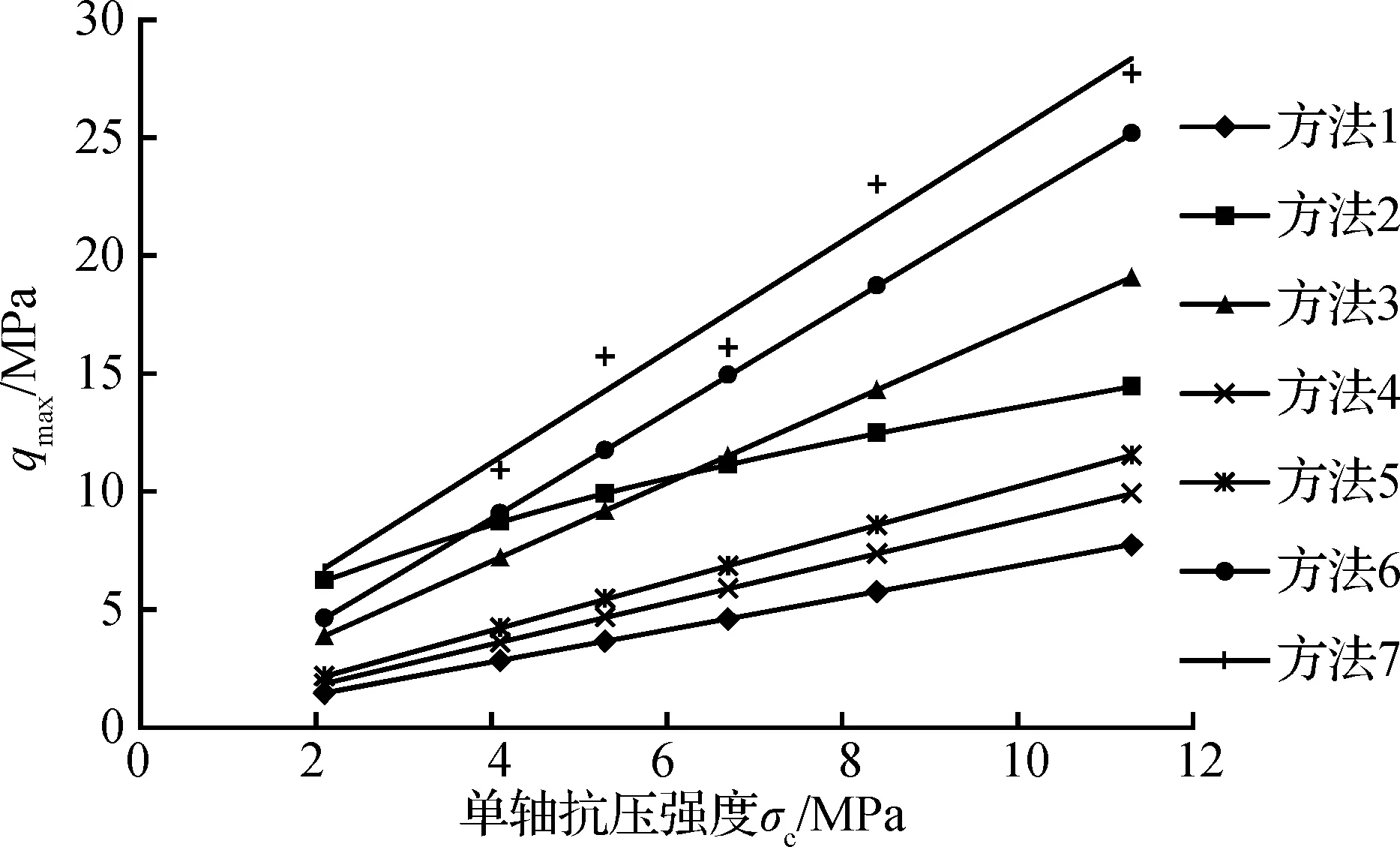
图3 各方法计算结果对比

由图3可以看出:各方法计算出的结果差异较为明显,其中方法1建筑桩基技术规范确定的承载力最小,也表明规范最为保守;而本文提出的4种计算方法(方法3～方法6)的结果比较接近实测值,尤其是方法6基于Ⅰ-Ⅱ型复合判据的桩周岩体微裂纹断裂极限承载力计算结果与实测值最为接近,说明本文所提出的4种方法较规范方法更为准确.

方法3是考虑桩端整体滑裂破坏,方法4和方法5是考虑桩周岩体剪切破坏,而方法6是假定桩周岩体微裂纹断裂,可以明显发现，方法6比其他3种方法的计算结果要大得多,而采用方法4和方法5的计算结果最小,这主要由于各方法假定的破坏模式和破坏准则判据不同.桩周岩体微裂纹断裂是微观尺度破坏,且考虑岩体内裂隙壁面摩擦效应的Ⅰ-Ⅱ型复合判据需要较大极限荷载作用,而桩周岩体剪切破坏是基于极限弹性破坏假定,认为岩体弹性状态后即破坏,未考虑弹性后的强度使承载力计算结果偏小.同时采用线性拟合由各计算方法得到的桩端岩体的极限承载力与岩石单轴抗压强度σc的关系,发现二者之间具有较好的线性相关性.

4 大直径嵌岩桩嵌岩深度与桩径对桩端极限承载力的影响

4.1 嵌岩深度对桩端极限承载力的影响

基于方法1～方法6分别计算嵌岩深度hr变化时对桩端岩体的极限承载力的影响,考虑到实际工程中嵌岩桩的嵌岩比一般不小于1,hr取为1.0～10.0 m,桩径d取为1.0 m,其余参数按表1中的工况6取值,计算结果如图4所示.

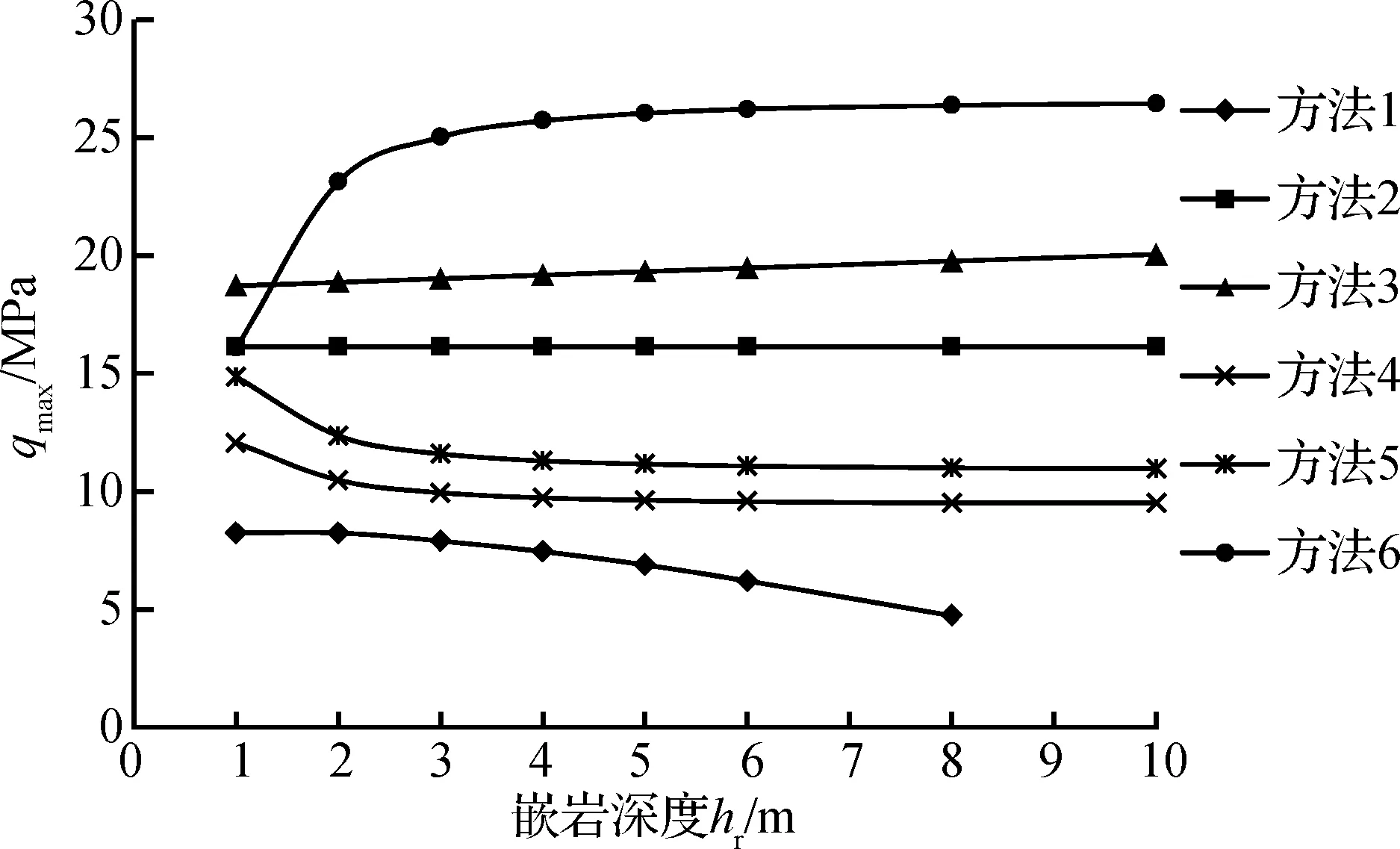
图4 嵌岩深度-桩端极限荷载关系曲线

通过图4的计算结果可以看出,当嵌岩深度hr变化时由不同方法计算得到的桩端岩体极限承载力变化规律差异明显:① 由建筑桩基技术规范确定的桩端极限承载力设计值(方法1)和基于二维、三维H-B准则的桩周岩体剪切破坏极限承载力计算方法(方法4和5)得到的岩体极限承载力都随嵌岩深度hr的增大呈递减的趋势,且后2种方法的计算结果趋于一常数.② 由式(2)取中间值的计算方法2未考虑嵌岩深度hr的影响,故其计算结果为一定值.③ 基于二维H-B准则的桩端岩体整体滑裂破坏的极限承载力计算方法3考虑了嵌岩深度hr的影响,因其考虑了上覆岩土层的自重对嵌岩桩桩端岩石承载力的影响,因而比较符合工程实际.④ 基于Ⅰ-Ⅱ型复合断裂判据的方法6得到的桩端岩体极限承载力随嵌岩深度hr的增大呈递增的趋势,这与岩石在三向受压时强度会较大提高的事实相符合.

4.2 桩径对桩端极限承载力的影响

基于方法1～方法6分别计算桩径d对桩端极限承载力的影响,桩径d取为0.8～2.5 m,嵌岩深度hr为1.0 m,其余参数按表1中的工况6取值,计算结果如图5所示.

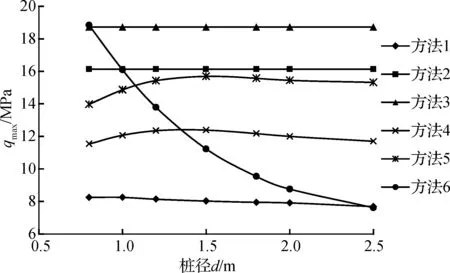
图5 桩径-桩端极限承载力关系曲线

由图5可以看出,当桩径d变化时由不同方法计算得到的桩端岩体极限承载力变化规律差异较大,甚至趋势相反:① 方法1的计算结果随桩径d的增大而缓慢减小,说明桩基规范对大直径嵌岩桩桩端承载力基本上未考虑桩径的影响.② 方法2和方法3未考虑桩径d的影响,故其计算结果为一定值.③ 方法4、方法5和方法6考虑了桩径d的影响,但所呈现趋势完全不同.文献[19]基于现场试验得到的大直径嵌岩桩的桩端极限承载力随桩径d的增大而减小,方法6计算得到的桩径-桩端极限荷载关系曲线更加符合现场实测规律.

5 结论

1) 本文假定了大直径嵌岩桩桩端岩体破坏可能的3种极限状态,提出基于二维H-B准则的桩端岩体整体滑裂破坏、基于二维和三维H-B强度准则的桩周岩体剪切破坏、基于Ⅰ-Ⅱ型复合判据的桩周岩体微裂纹断裂的4种大直径嵌岩桩桩端岩体承载力的计算方法,可为大直径嵌岩桩桩端岩体的桩端极限承载力分析与设计提供理论依据.

2) 通过引用文献中试验数据作为验证参照,现行的嵌岩桩桩端承载力计算方法较偏于保守,本文提出的4种计算方法比较接近实测值,尤其是基于Ⅰ-Ⅱ型复合判据的桩周岩体微裂纹断裂的桩端极限承载力计算结果与实测值最为接近.

3) 大直径嵌岩桩的桩端极限承载力存在明显的尺寸效应,与嵌岩深度与桩径密切相关.研究表明，桩端极限荷载与嵌岩深度及桩径密切相关,嵌岩桩桩端极限荷载随嵌固深度的增大而增大,而随桩径的增大而减小.4种计算方法中基于Ⅰ-Ⅱ型复合判据的桩周岩体微裂纹断裂计算方法与现场实测规律更加相符.

)

[1] 龚维明, 戴国亮, 宋晖. 大直径深长嵌岩桩承载机理研究与应用[M]. 北京:人民交通出版社, 2010:1-10.

[2] Leung C F, Ko H Y. Centrifuge model study of piles socketed in soft rock[J].SoilsandFoundations, 1993,33(3):80-91. DOI:10.3208/sandf1972.33.3_80.

[3] 中华人民共和国住房和城乡建设部. JGJ 94—2008建筑桩基技术规范[S]. 北京:中国建筑工业出版社, 2008.

[4] Zhang L Y, Einstein H H. End bearing capacity of drilled shafts in rock[J].JournalofGeotechnicalandGeoenvironmentalEngineering, 1998,124(7):574-584. DOI:10.1061/(ASCE)1090-0241(1998)124:7(574).

[5] Hoek E, Wood D, Shah S. A modified Hoek-Brown failure criterion for jointed rock masses[C]//ProceedingsoftheRockCharacterizationSymposiumofISRM. London:British Geotechnical Society, 1992:209-214. DOI:10.1680/rc.35621.0037.

[6] Hoek E, Carranza-Torres C, Corkum B. Hoek-Brown failure criterion—2002 edition[C]//ProceedingsoftheNorthAmericanRockMechanicsSocietyNARMS-TAC. Toronto,Canada:University of Toronto Press, 2002: 267-273.

[7] 朱合华, 张琦, 章连洋. Hoek-Brown强度准则研究进展与应用综述[J]. 岩石力学与工程学报, 2013, 32(10):1945-1963.

Zhu Hehua, Zhang Qi, Zhang Lianyang. Review of research progresses and applications of Hoek-Brown strength criterion [J].ChineseJournalofRockMechanicsandEngineering, 2013,32(10):1945-1963. (in Chinese)

[8] 李镜培, 王勇刚. 嵌岩桩桩端承载力探讨[J]. 力学季刊, 2006, 27(1):118-123. DOI:10.3969/j.issn.0254-0053.2006.01.016.

Li Jingpei, Wang Yonggang. Study of tip resistance on rock socketed pile[J].ChineseQuarterlyofMechanics, 2006,27(1):118-123. DOI:10.3969/j.issn.0254-0053.2006.01.016. (in Chinese)

[9] 董鑫, 白良, 肖建军, 等. 应力空间内主应力及主方向的解析表达式[J].昆明理工大学学报(理工版), 2004, 29(1):89-92,96. DOI:10.3969/j.issn.1007-855X.2004.01.023.

Dong Xin, Bai Liang, Xiao Jianjun, et al. Parsed currency formula of main stress and main direction in stress space[J].JournalofKunmingUniversityofScienceandTechnology(ScienceandTechnology), 2004,29(1):89-92,96. DOI:10.3969/j.issn.1007-855X. 2004.01.023. (in Chinese)

[10] Zhang L Y, Zhu H H. Three-dimensional Hoek-Brown strength criterion for rocks[J].JournalofGeotechnicalandGeoenvironmentalEngineering, 2007,133(9):1128-1135. DOI:10.1061/(ASCE)1090-0241(2007)133:9(1128).

[11] Zhang L Y. A generalized three-dimensional Hoek-Brown strength criterion[J].RockMechanicsandRockEngineering, 2008,41(6):893-915. DOI:10.1007/s00603-008-0169-8.

[12] 唐辉明, 晏同珍. 岩体断裂力学理论与工程应用[M]. 武汉:中国地质大学出版社, 1993:8-18.

[13] 潘别桐, 唐辉明. 岩石压剪性断裂特性及Ⅰ-Ⅱ型复合断裂判据[J]. 地球科学——中国地质大学学报, 1988, 13(4):413-421.

Pan Bietong, Tang Huiming. The characteristics of the compression-shear fracture in rocks and the Ⅰ-Ⅱ composite fracture criterion[J].EarthScience—JournalofChinaUniversityofGeosciences, 1988,13(4):413-421. (in Chinese)

[14] 李世愚. 岩石断裂力学导论[M]. 合肥:中国科学技术大学出版社, 2010:99-107.

[15] 郑安兴, 罗先启. 压剪应力状态下岩石复合型断裂判据的研究[J]. 岩土力学, 2015, 36(7):1892-1898. DOI:10.16285/j.rsm. 2015.07.009.

Zheng Anxing, Luo Xianqi. Research on combined fracture criterion of rock under compression(shear stress[J].JournalofRockandSoilMechanics, 2015,36(7):1892-1898. DOI:10.16285/j.rsm.2015.07.009.(in Chinese)

[16] Zhang Z X. An empirical relation between mode Ⅰ fracture toughness and the tensile strength of rock[J].InternationalJournalofRockMechanicsandMiningSciences, 2002,39(3):401-406. DOI: 10.1016/S1365-1609(02)00032-1.

[17] Gercek H. Properties of failure envelopes and surfaces defined by the Hoek-Brown failure criterion[C]//Proceedingsofthe6thRegionalRockMechanicsSymposium. Konya, Republic of Turkey， 2002: 3-11.

[18] 冯增朝, 赵阳升.岩体裂隙尺度对其变形与破坏的控制作用[J].岩石力学与工程学报, 2008, 27(1): 78-83.DOI: 10.3321/j.issn: 1000-6915.2008.01.012.

Feng Zengzhao, Zhao Yangsheng.Control effect of fissure scale on deformation and failure of rock mass[J].ChineseJournalofRockMechanicsandEngineering, 2008,27(1): 78-83.DOI: 10.3321/j.issn: 1000-6915.2008.01.012.(in Chinese)

[19] 龚成中.大直径嵌岩桩基承载特性的理论分析和实验研究[D].南京: 东南大学土木工程学院, 2014.