人行荷载模型与人致结构振动试验研究

操礼林 钱 程 张志强 李爱群,3

(1江苏大学土木工程与力学学院, 镇江 212013)(2东南大学土木工程学院, 南京 210096)(3北京建筑大学土木与交通工程学院, 北京 100044)

随着轻质、低阻尼、大跨度结构的不断增多,人行荷载激励作用导致的结构振动舒适性问题日益凸显,若设计处理不当将对结构的适用性甚至安全性造成严重威胁[1-3]．为准确预测人行荷载激励下大跨结构的振动响应、评估结构是否满足振动舒适性要求,需要建立合理的人行荷载模型．

Rainer等[4]开展了3名受试者单人行走荷载试验,并采用四阶谐波形式的傅里叶级数初探了人行荷载的数学模型．Kerr等[5]采用测力板采集了40名志愿者的1 000余条单步行走竖向荷载时程曲线．国外研究者采用傅里叶级数形式表达人行荷载激励力,不同学者采用的函数表达式存在一定差异[6-8]．樊健生等[9]基于欧美人体测试数据采用傅里叶级数建立了行人正常步行状态下的标准荷载激励模型．谢伟平等[10]采用测力板系统开展了车站候车厅单人行走步行力测试．陈隽等[11]采用三维动作捕捉技术开展了100人次的单人行走荷载试验,提出了人行荷载模型的动荷载因子和相位角等参数取值．可靠的人行荷载模型是确保大跨结构人致振动响应分析准确性的前提．目前，国内学者在进行人致振动舒适度设计或计算分析时一般选用国外的荷载模型,然而不同国家人体步行特征参数存在一定差异,研究符合我国人体步行特点的人行荷载模型及人致结构振动试验具有重要意义．

本文基于实测动荷载因子统计值,构建了人行荷载傅里叶级数模型,进而建立大跨楼盖人致振动分析方法,开展了模型结构人致振动试验研究．

1 人行荷载的傅里叶级数模型

假定人行走时保持一定的步伐,即步频、相位角等步行参数均保持不变,行走激励产生的步行荷载为周期函数．行人脚步力荷载模型可以表达为静荷载与几个简谐动荷载之和的傅里叶级数模型[12-13],即

(1)

式中,f(t)为行人脚步力荷载;t为时间;fs为人行走的步频,计算竖向荷载时为行人每秒钟落步数;G为行人体重,参考美国钢结构协会取为70 kg[2];αi为第i阶动荷载因子;φi为第i阶谐波的相位角,一般地取φ1=0,φ2=φ3=π/2．

各阶简谐波在总激励力中所占百分数随着阶数的增加而减小,高阶谐波动载因子减小迅速,实际应用时考虑前3阶简谐波已具有相当高的精度．基于实测的人行荷载曲线试验结果可知,动荷载因子值分布较离散,且总体上呈现对数正态分布[14]．统计分析得到具有75%保证率的前3阶动荷载因子取值分别为0.433 5fs-0.372 2,0.186 6和0.115 3．

2 大跨楼盖人致振动分析方法

根据结构动力学原理[15],楼盖结构某时刻人行荷载作用下的振动方程可表示为

(2)

运用标准模态坐标变换可得

y=Φq

(3)

ΦTmΦ=I

(4)

式中,Φ为关于质量的归一化模态矩阵．

将式(3)和(4)代入式(2)中,运用阻尼比和频率表达刚度和阻尼,对其进行一定变换和处理后可得

(5)

人致结构振动分析时,获取已知关心楼盖区域及人行荷载作用处的模态及圆频率矩阵,采用Wilson-θ法编程求解式(5)得到楼盖的模态坐标,继而可分别求得位移及加速度等响应．人行荷载作用位置可能不位于节点上,采用样条插值方法得到人行荷载作用位置的模态位移．由于人行荷载加载空间和时间的变异性以及大跨楼盖布局和构造的复杂性,复杂工程分析时难以通过解析方法求得结构各点的人致振动响应．因此,结合有限元方法,在楼盖有限元模型上加载人行荷载并进行动力时程分析．

3 试验

3.1 构件设计

试验模型结构2个方向的跨度尺寸分别为7 700和4 700 mm,板平面的尺寸为8 000 mm×5 000 mm,板厚60 mm,混凝土强度等级为C30．主梁采用热轧普通I20b和I22b工字形钢,次梁采用热轧普通I12.6工字形钢,柱采用H300 mm×200 mm×6 mm×10 mm．构件设计满足承载力与正常使用阶段要求．为模拟大跨轻柔楼盖,设计时考虑降低楼板刚度并增大结构自重．试件钢框架结构布置示意图见图1．采用ANSYS有限元软件和环境随机振动法分别计算和实测了模型结构的动力特性,模拟分析和实测的模态分析结果见表1．试验测试仪器主要包括941-B型加速度传感器、安正AZ308信号采集箱、安正AZ808滤波器和安正AZ-CRAS动态信号测试分析系统．

图1 试件钢框架结构布置示意图

3.2 楼盖人致振动试验

3.2.1 试验过程

分别开展了单人和多人不同工况人行荷载作用下的模型楼盖结构人致振动响应试验研究．图2给出了部分人行荷载作用下模型楼盖结构振动试验情况．相关人致振动试验情况如下:

1) 1人沿路线3往返行走,试验者对楼盖结构产生的重力为0.62 kN;

2) 3人分别沿路线2、路线3和路线4往返行走,试验者对楼盖结构产生的重力分别为0.53,0.57,0.59 kN;

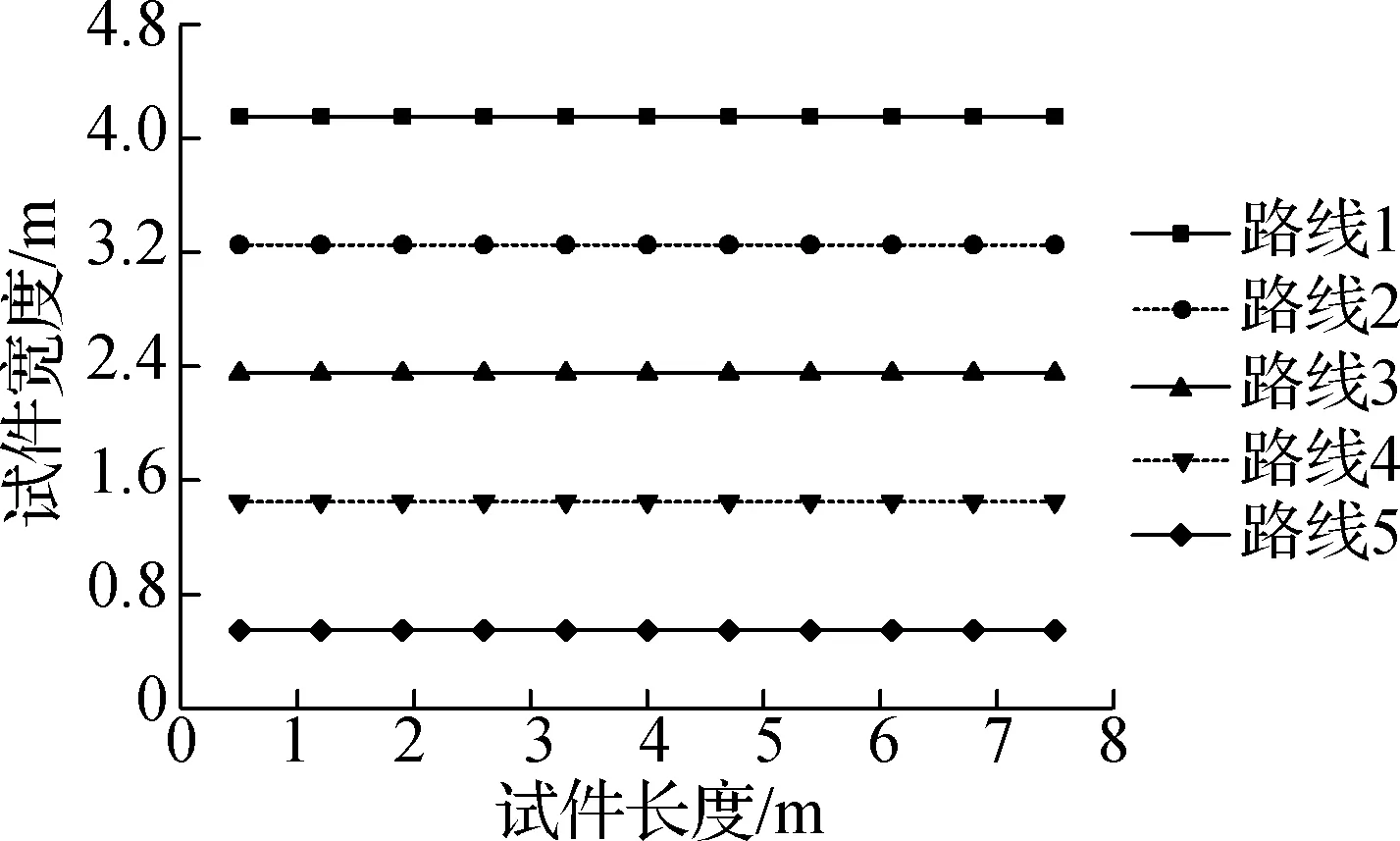
(a) 模型结构人群行走路线示意图

(b) 3人固定步频行走

(c) 5人自由行走

3) 5人分别沿路线1、路线2、路线3、路线4和路线5往返行走,试验者对楼盖结构产生的重力分别为0.65,0.57,0.59,0.62,0.67 kN;

4) 10人均沿路线1和路线5围成的口字型绕圈行走,试验者对楼盖结构产生的重力分别为0.65,0.57,0.59,0.62,0.67,0.65,0.52,0.58,0.67,0.53 kN．

3.2.2 试验结果及分析

模型结构实测的1人、3人、5人及10人自由行走和2.3 Hz步频同步行走时的模型结构楼盖中心点处的人致振动加速度响应见图3．由图3(a)

(a) 1人行走

(c) 5人行走

(d) 10人行走

可知,1人自由行走下的楼盖均方根加速度响应比2.3 Hz固定步频行走工况下的值小30%,这是因为2.3 Hz步频的倍频与模型结构基频4.635 Hz较为一致,从而使模型结构对应的模态被激起共振,而人自由行走步频与共振频率则存在较大差值．由图3(b)～(d)可知,3人、5人和10人按2.3 Hz固定步频肩并肩同步行走工况下的楼盖均方根加速度响应分别为自由行走工况下的值的2.10,2.43,3.10倍．由于2.3 Hz步频的倍频与模型结构基频一致,且多人是按照指令同步调行进,步行激励力叠加放大,故结构对应的模态被激起共振;相反,多人自由行走时步频和相位不同,步行激励力谐波叠加后减小,而且自由行走步频的倍频与模型结构的基频相差较大,导致该工况下的楼盖加速度响应较小．

进一步分析图3可知,随着自由行走人员数量的增多,模型结构均方根加速度响应略有增大,10人自由行走下楼盖均方根加速度响应值比3人自由行走下时增大20.4%,这是因为随着行走人员数量的增多,不同步调和相位的步行激励力叠加后抵消显著,结构均方根加速度响应与人群数量增加值不是简单的线性放大关系;然而,当试验者按2.3 Hz固定步频同步行走时,人行荷载激起结构模态共振,且行人同步调一致行进致使步行激励力叠加放大效果明显,导致该工况下楼盖均方根加速度响应随着同步行走人员数量增加而明显增大．其中,10人按2.3 Hz固定步频同步行走下的结构均方根加速度响应值为1人行走时的4.1倍．

4 理论分析与试验结果比较

采用建立的人行荷载模型及人行荷载加载分析模式,基于动力时程分析方法对2人、4人、8人自由行走和2.3 Hz步频同步行走下模型结构振动加速度响应进行计算分析,板中心位置点加速度响应时程分析结果和实测结果见图4．人行走路径情况如下:

1) 2人行走路径分别为图2(a)中路线2和路线4,试验者对楼盖结构产生的重力分别为0.65和0.62 kN;

2) 4人行走路径分别为图2(a)中路线1、路线2、路线4和路线5往返行走,试验者对楼盖结构产生的重力分别为0.65,0.53,0.57,0.59 kN;

3) 8人行走路径分别为图2(a)中路线1、路线2、路线4和路线5,两侧各4人相向而行,试验者对楼盖结构产生的重力分别为0.65,0.57,0.59,0.62,0.67,0.65,0.58,0.67 kN．

根据图4的计算结果和相应实测结果对比分析可知,不同工况下人致振动加速度响应计算分析结果与人行荷载试验实测结果吻合较好,加速度响应峰值和平均值比较一致,从而验证了本文建立的人行荷载模型及人致振动响应分析方法的正确性．

(a) 2人自由行走

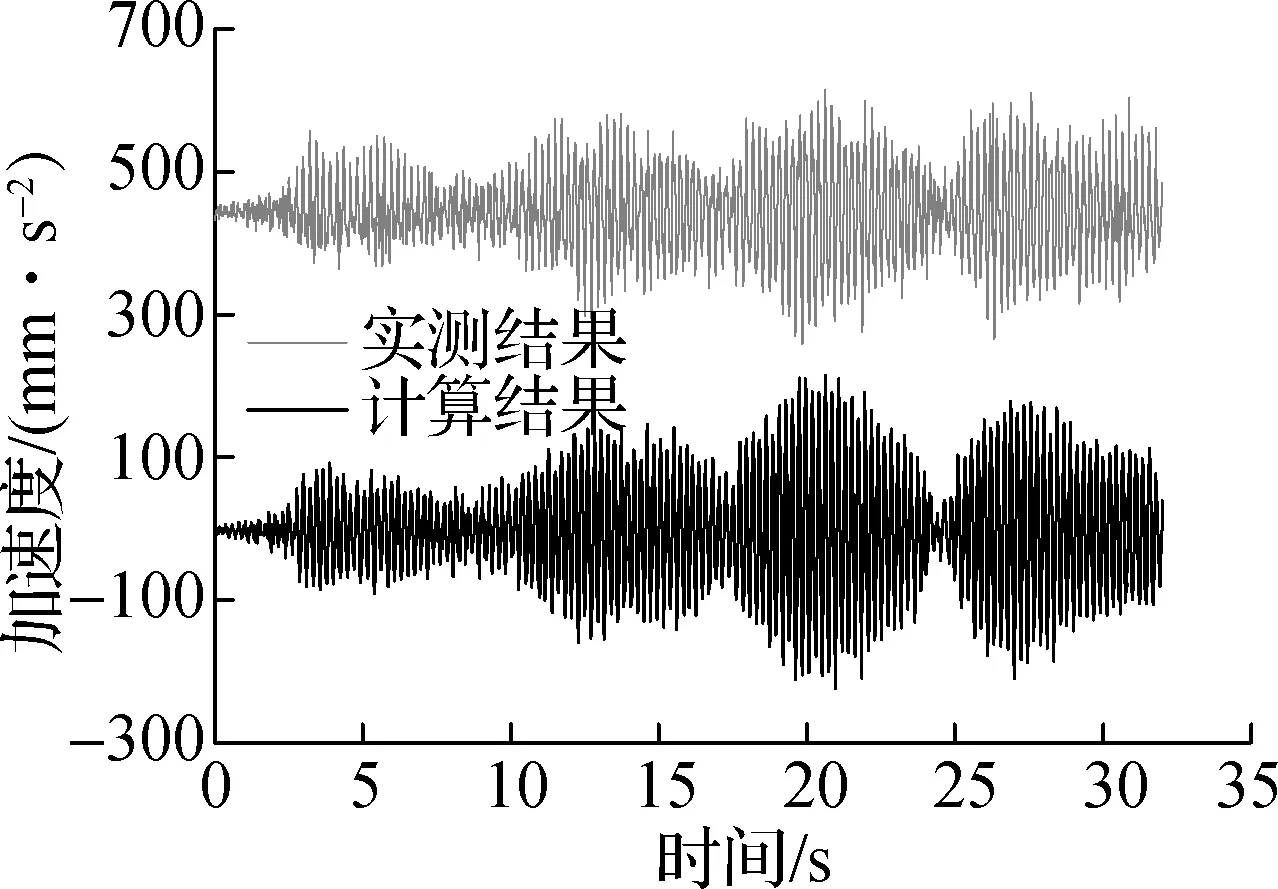
(b) 2人2.3 Hz固定步频行走

(c) 4人自由行走

(d) 4人2.3 Hz固定步频行走

(e) 8人自由行走

(f) 8人2.3 Hz固定步频行走

5 结论

1) 不同工况人行荷载作用下的模型结构人致振动试验结果与模拟计算分析结果吻合较好,建立的人行荷载模型及大跨度楼盖结构人致振动响应分析方法具有较好的适用性．

2) 试验结果表明,按固定步频行走的人行荷载作用下楼盖振动加速度响应大于自由行走时的人行荷载作用效应;随着自由行走人员数量增多,模型结构均方根加速度响应值略有增大,但增大值与行人数量增加值不是简单的线性放大关系．

3) 多人按结构基频一半的固定步频同步行走时将激起结构模态共振,且同步调一致行进会使步行激励力叠加放大效果显著,导致楼盖结构均方根加速度响应随着同步行走人员数量增加而明显增大．

)

[1] van Nimmen K, Lombaert G, de Roeck G, et al. Vibration serviceability of footbridges: Evaluation of the current codes of practice[J].EngineeringStructures, 2014,59: 448-461. DOI:10.1016/j.engstruct.2013.11.006.

[2] Jones C A, Reynolds P, Pavic A. Vibration serviceability of stadia structures subjected to dynamic crowd loads: A literature review[J].JournalofSoundandVibration, 2011,330(8): 1531-1566. DOI:10.1016/j.jsv.2010.10.032.

[3] 操礼林, 李爱群, 张志强, 等. 大跨度组合楼盖人致振动分析与实测研究[J]. 西南交通大学学报, 2012, 47(6): 922-928. DOI:10.3969/j.issn.0258-2724.2012.06.003.

Cao Lilin, Li Aiqun, Zhang Zhiqiang, et al. Human-induced vibration analysis and measurement of long-span composite floors[J].JournalofSouthwestJiaotongUniversity, 2012,47(6): 922-928. DOI:10.3969/j.issn.0258-2724.2012.06.003.(in Chinese)

[4] Rainer J H, Pernica G, Allen D E. Dynamic loading and response of footbridges[J].CanadianJournalofCivilEngineering, 1988,15(1): 66-71. DOI:10.1139/l88-007.

[5] Kerr S C, Bishop N W M. Human induced loading on flexible staircases[J].EngineeringStructures, 2001,23:37-45.

[6] Racic V, Pavic A, Brownjohn J M W. Modern facilities for experimental measurement of dynamic loads induced by humans: A Literature review [J].ShockandVibration, 2013,20(1): 53-67. DOI:10.1155/2013/975956.

[7] Racic V, Pavic A, Brownjohn J M W. Experimental identification and analytical modeling of human walking forces: Literature review[J].JournalofSoundandVibration, 2009,326(1): 1-49. DOI:10.1016/j.jsv.2009.04.020.

[8] Tubino F, Piccardo G. Tuned mass damper optimization for the mitigation of human-induced vibrations of pedestrian bridges[J].Meccanica, 2014,50(3): 809-824. DOI:10.1007/s11012-014-0021-z.

[9] 樊健生, 陈宇, 聂建国. 人行桥标准行人激励荷载的构建与验证[J]. 计算力学学报, 2012, 29(4): 538-544.

Fan Jiansheng, Chen Yu, Nie Jianguo.Modeling and confirmation of pedestrian induced walking load on footbridge[J].ChineseJournalofComputationalMechanics, 2012,29(4): 538-544. (in Chinese)

[10] 谢伟平, 何卫, 艾康伟. 车站结构人行荷载特性研究[J]. 工程力学, 2012, 29(12): 256-264.

Xie Weiping, He Wei, Ai Kangwei. Study on characteristics of pedestrian loads of railway station structures[J].EngineeringMechanics, 2012,29(12): 256-264. (in Chinese)

[11] 陈隽, 彭怡欣, 王玲. 基于步态分析技术的三向单足落步荷载曲线试验建模[J]. 土木工程学报, 2014, 47(3): 79-87.

Chen Jun, Peng Yixin, Wang Ling. Experimental investigation and mathematical modeling of single footfall load using motion capture technology[J].ChinaCivilEngineeringJournal, 2014,47(3): 79-87. (in Chinese)

[12] 陈政清, 华旭刚. 人行桥的振动与动力设计[M]. 北京: 人民交通出版社, 2009:44-48.

[13] 杨康. 基于人-结构相互作用大跨楼盖振动响应及控制研究[D].南京:东南大学土木工程学院,2015.

[14] 魏结强. 单人行走荷载模拟及大跨楼盖振动响应与控制研究[D].南京:东南大学土木工程学院,2015.

[15] Clough R, Penzien J．结构动力学[M].2版.王光远,等译.北京:高等教育出版社, 2010:173-192.