单连杆柔性关节机械臂的高阶滑模控制器设计
谢仕堉,孙 伟
(聊城大学 数学科学学院,山东 聊城 252059)
0 引言
早在上世纪五六十年代,前苏联学者Utkin和Emelyanov就提出滑模控制的概念[1]。近年来,滑模控制因其控制结构简单、强鲁棒性等优点逐渐成为许多专家学者的研究热点。滑模控制本质上是一类特殊的非线性控制方法,其主要特征还表现为控制的非连续性。滑模控制使被控系统的状态有目的变化,即闭环系统按照预定的滑动模态轨迹运动并到达指定位置。滑动模态是指滑模控制闭环系统发生在滑动模态面(空间中的一类超平面,简称滑模面)上的运动形式。一般地,滑模控制闭环系统的运动包括到达和滑动两个阶段,即系统状态在有限时间内到达滑模面,然后沿着滑模面滑动到系统平衡点。随着研究的深入,二阶滑模控制理论(SOSM)在前期理论的基础上发展起来[2,3]。与传统的一阶滑模方法相比,二阶滑模具有削弱抖振的优点。然而,SOSM控制算法的局限性在于滑动变量的相对程度为2,限制了该算法的应用的范围。因此,研究任意阶次的高阶滑模控制算法具有重要的意义。
高阶滑模(HOSM)的概念由Arie Levant在20世纪80年代提出[4]。与传统一阶滑模控制相比,高阶滑模的本质在于避免相对阶限制问题并削弱抖振,且能保留滑模控制的强鲁棒性、抗干扰性等优点。与现有的模糊控制[5, 6]、超螺旋算法[7]、自适应控制[8-10]、非周期采样控制[11]等方法不同,现在发展的高阶滑模控制理论弥补了控制理论存在的不足并得到了广泛的应用。目前,HOSM理论已应用于电气动执行器[12]、降压变换器[13]、自动驾驶汽车[14]等多个领域。因此,HOSM方法不仅仅是对传统滑模控制理论的进一步推广,而且有着广泛的实际应用背景[15-21]。
柔性关节机械臂是一个非线性、强耦合的复杂系统,具有精度高、能耗低、质量轻和工作效率高等特点。同时,柔性关节机械臂还具有较好的可控性,因此在许多领域具有很高的应用价值。在一些工业领域,有时并不需要机械手臂具有完整的六个自由度,而只需其中的一个或几个自由度。例如,直角坐标系机械臂可以由单轴机械手臂组合而成,使用单轴机械臂有很多的优点,其中最为重要的一点是单轴机械臂能够大大降低工业设计的成本,因此越来越多的研究者从控制算法等角度研究单连杆柔性关节机械臂[22-24],使得单连杆柔性关节机械臂系统在控制领域成为一个热点话题。
由于不确定性问题在许多实际系统中是不可避免的,柔性关节机械臂系统也不例外。那么通过高阶滑模控制技术可以有效削弱柔性关节机械臂系统不确定性带来的影响。本文主要研究高阶滑模控制对于单连杆柔性关节机械臂系统的镇定控制问题,创新点和研究意义主要有以下三个方面。(1)针对柔性关节机械臂系统设计的高阶滑模控制器,避免了一阶滑模中存在的相对阶限制的问题,扩展了滑模控制的应用范围。(2)利用构造的李雅普诺夫函数,使系统的输出信号始终保持在有限时间内收敛。(3)与文献[24]相比,本文将高阶滑模算法应用到单连杆柔性关节机械臂系统,用实例验证该算法的有效性和优越性,对于单连杆机械臂的算法研究具有重要意义。
符号表示R表示所有实数的集合,Rn表示n维的欧几里德空间,[x]α=sign(x)|x|α。
1 系统描述及引理
本文以欧拉-拉格朗日方程为基础,用以下动力学模型描述单连杆柔性关节机械臂[26, 27]

(1)
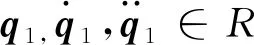
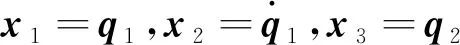
(2)
式中xi∈R,i=1,2,3,4为系统状态。
滑动变量s是系统输出,令
将系统转换为
(3)
式中s(4)=J-1M-1(x1)K(-Bx4-K(x3-x1))+M-1(x1)(-C(x1,x2)-G(x1)-M-1(x1)Kx3+M-1(x1)(-C(x1,x2)-G(x1)-F(x2)-Kx1)))+J-1M-1(x1)Ku。且A(t,x)=J-1M-1(x1)K(-Bx4-K(x3-x1))+M-1(x1)(-C(x1,x2)-G(x1)-F(x2)-K(M-1(x1)Kx3+M-1(x1)(-C(x1,x2)-G(x1)-F(x2)-Kx1)))和B(t,x)=J-1M-1(x1)K是光滑函数。
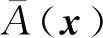
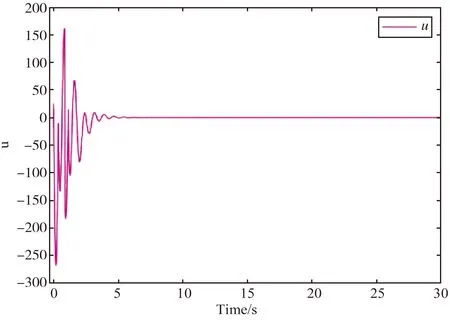
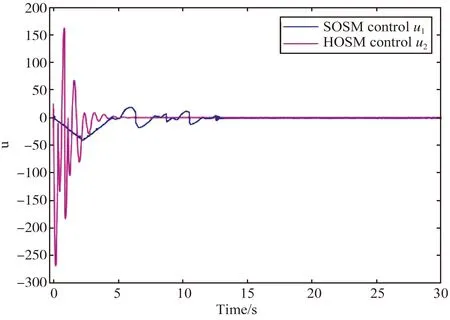
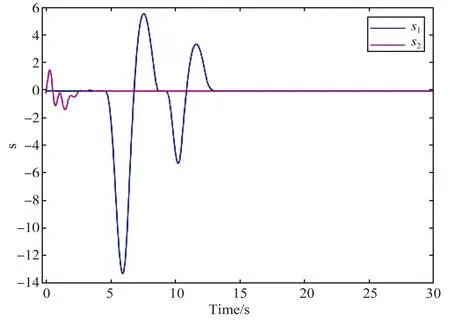
引理1[28]如果p1>0和0 |[x]p1p2-[y]p1p2|≤21-p2|[x]p1-[y]p1|p2。 引理2[29]设c和d为正的常数。给定任意实数γ>0,得到 引理3[30]对于∀xi∈R,i=1,2,3,…,n,不等式成立(|x1|+…+|xn|)p≤|x1|p+…+|xn|p。 定理若系统(1)满足假设1,则存在常数βi>0,i=1,2,3,4,建立HOSM控制器 (4) 证明第一步,选择候选李雅普诺夫函数 (5) 对V1沿系统(1)求时间的导数可得 (6) (7) (8) 将上式代入(8)式可得 (9) (10) 由引理2可得 (11) 第三步,选择候选李雅普诺夫函数 (12) (13) (14) 注意,(3)式中后两项可以合成一项,由引理1和引理2可得 (15) (16) 式中η2是一个正的常数。 由引理2,可以推出 (17) (18) 第四步,选择候选李雅普诺夫函数为 (19) (20) 进一步,(20)式中的两项通过引理1和引理2,可化简为 (21) (22) (23) (24) 将(21)和(24)代入(20)式,可得 (25) (26) 注意,根据(7)式,(12)式以及(19)式可得 针对单连杆柔性关节机械臂系统[32] (27) 表1 单连杆柔性关节机器人系统的参数 (28) 仿真结果如图1,2所示。图1为本文所定义的滑动变量s随时间t的变化曲线,不难发现,在本文提出的高阶滑模控制器作用下,滑动变量s能够快速精准的收敛到零。保证快速、高效的实现镇定,有助于提升系统的鲁棒性。图2表示的是控制输入u的曲线,当系统出现干扰影响时,控制器会迅速响应,削弱不确定性造成的抖振现象,快速收敛,极大地提高了对柔性关节机械臂系统的控制性能。 图2 控制输入u的轨迹 为了更好地说明所提方法的优越性,我们对单连杆柔性关节机械臂系统设计的算法与文献[33]中提出的SOSM控制方法进行仿真比较,模拟结果如图3,4所示。 图3 HOSM控制器μ1和SOSM控制器μ2的轨迹 从图3和图4可以看出,虽然两种控制方法都能获得良好的控制性能,但是本文研究的HOSM控制方法使滑动变量s收敛速度更快、时间更短、控制器的响应更加迅速。因此,与文献[33]中SOSM控制方法相比,本文研究的HOSM控制方法具有更好地收敛性,大大缩短了系统的响应时间。此外,从图3,4中可以清楚地看出,在HOSM控制器的作用下,滑动变量s抖振幅度小、收敛快,说明本文提出的HOSM控制器能更好地抑制扰动的影响,削弱抖振现象。综上所述,实现了预期的控制目标。同时,对比仿真结果证明了高阶滑模控制算法应用于单连杆柔性关节机械臂系统的优越性。 图4 在HOSM控制器u1和SOSM控制器u2条件下滑动变量s1和s2的轨迹 本文针对单连杆柔性关节机械臂系统设计了一个高阶滑模控制器。通过设计的李雅普诺夫函数,保证输出信号在有限时间内收敛到零。其次,在控制器中引入符号函数抑制了抖振现象。最后,通过有限时间理论和李雅普诺夫稳定性理论,证明了该控制算法能够使单连杆柔性关节机械臂系统在有限时间内实现镇定控制。通过一个仿真例子证明了所提出控制算法的有效性。未来的工作将集中于将该方法扩展到n-连杆机械臂系统的控制问题。2 主要结果
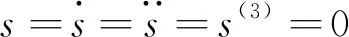
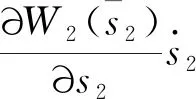


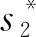
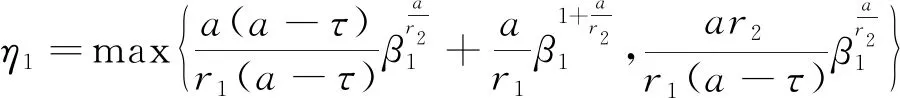
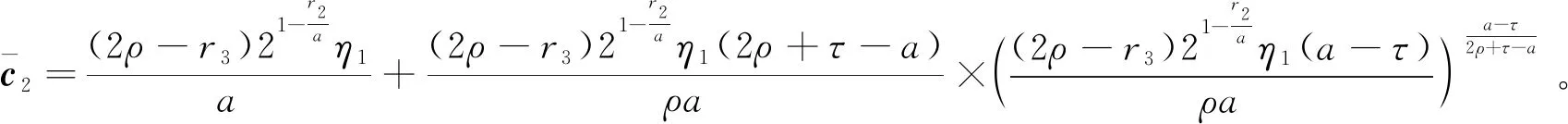
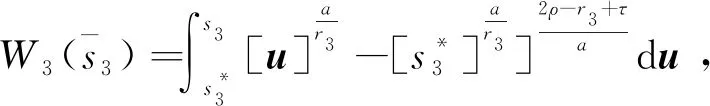
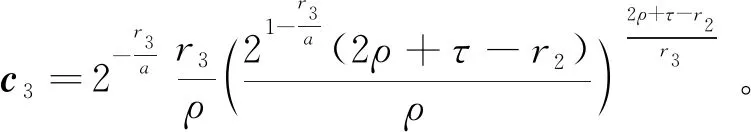
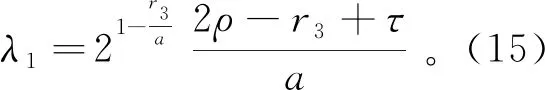
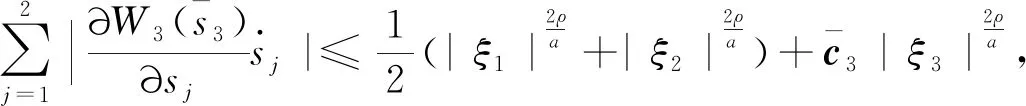
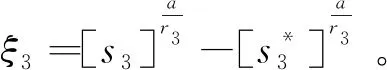

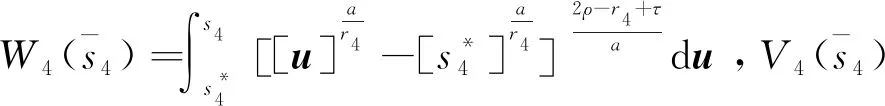

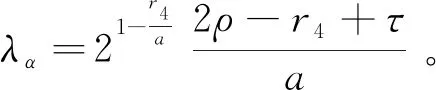
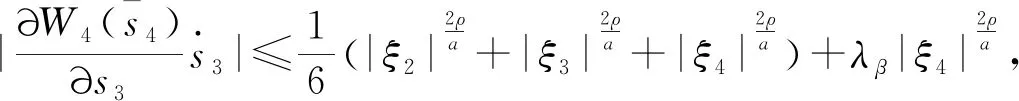


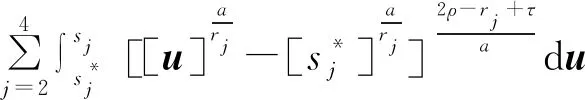
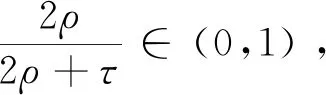
3 仿真例子

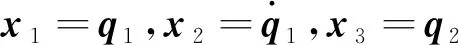
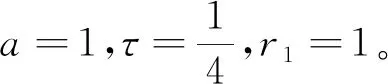
4 结论

