颗粒土中剪切带临界状态数学描述及其完全解*
黄文雄, 崔 贤
(河海大学 力学与材料学院, 南京 210098)
0 引 言
临界状态在土力学中指土体剪切失效时所趋近的无剪胀塑性流动状态.土体的临界状态只与土的物理特性及作用于土体的平均压力有关,不依赖土体的初始密度,因此是建立土体本构模型的重要参考状态[1-2].
土体均匀趋于临界状态的失效模式只是一种理想的情形,实际土体破坏往往伴随着剪切带的发展.这种集中于带状区域的应变局部化的形成和演化是认识土体结构失效与破坏的关键,也一直是土力学与颗粒材料力学所关注的研究课题.相对于土体结构的宏观尺度,剪切带的厚度是很小的,实验所观察到的剪切带厚度约为土体颗粒平均粒径的10~15倍左右[3-4].因此,剪切带两侧有限的相对剪切位移就可在带内引起较大的剪切变形,使得带内材料很快达到临界状态.
经典连续介质本构模型不包含任何与材料细观结构相关的特征长度,预测的剪切带理论厚度为零.因此,常规的土体本构模型只能预测剪切带的产生[5-6],一般不能规范剪切带的厚度并正确预测土体涉及剪切带演化的后失效行为.在采用有限元等方法分析土体的后失效行为时,数值解具有网格尺寸依赖性.
为克服上述困难,可采用高阶连续介质力学理论,如微极场理论[7]、高阶梯度理论[8]等.高阶连续介质力学模型允许引入材料细观特征长度,可以在一定程度上刻画材料中应力和变形在细观尺度上的变化.其中Cosserat介质属于微极连续介质力学理论中较简单的一种, 通过在连续体中引入质点的转动自由度和偶应力,可以在一定程度上描述材料细观尺度上的应力和变形的变化,从而能恰当模拟剪切带的发展.Mühlhaus和Vardoulakis[9]采用Cosserat介质弹塑性模型讨论了土体中剪切带厚度与颗粒平均粒径的关系;Oda[10]研究了颗粒材料细观结构、偶应力与剪切带的关系;Huang等[11]基于Cosserat介质理论,将Gudehus[12]和Bauer[13]所建立的模拟砂土等颗粒土的亚塑性模本构型推广为微极亚塑性模型,并用于砂土中局部化应变发展模式的数值分析[14].
基于文献[11]建立的微极亚塑性模型,Huang和其合作者[15]分析了颗粒材料在平面Couette剪切中,条形区域内的应变局部化的形成与演化机制,并且针对充分发展的平直剪切带,推导得到了临界状态下的控制方程,但针对该控制方程并未得到完全解.本文主要目的是在前期工作[15]的基础上,探讨剪切带在临界状态下的关键变量,即Cosserat转动角速度所满足的非线性常微分方程的主要特性及求解途径,并给出问题的完全解.
1 微极亚塑性模型简述

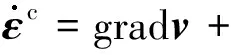
(1)
Cosserat介质中的应力张量σ和偶应力张量μ满足平衡方程:
divσ+b=0, divμ-∶σ=0,
(2)
其中,b为体力矢量;grad代表矢量和张量的梯度运算,div代表散度运算;为置换符号;点乘积运算代表两个张量相邻的一对下标的缩并,双点积运算代表两个张量前后两对对应下标的缩并.式(1)和(2)也表明Cosserat介质中的应力、偶应力、应变率和微曲率率张量在一般情况下是非对称的.
Gudehus[12]和Bauer[13]以Cauchy应力σ和孔隙比e为状态变量,建立了一个有效实用的临界状态亚塑性模型(G-B模型),能较好地模拟砂土等无黏性颗粒土的力学响应.为了能客观模拟颗粒土中剪切带的形成与发展,Huang等[11]基于 Cosserat介质理论将G-B模型推广为微极亚塑性模型,用下列张量方程描述Cauchy应力及偶应力张量的客观时间导数与应变率、微曲率率张量之间的关系:
(3)
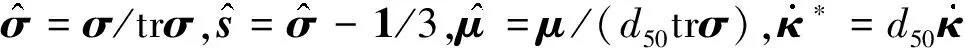
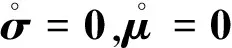
(4)
(5)
(6)
式(5)和(6)实际为建立模型时预设的临界状态流动法则和强度条件[11].
2 剪切带内临界状态的数学描述
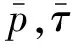
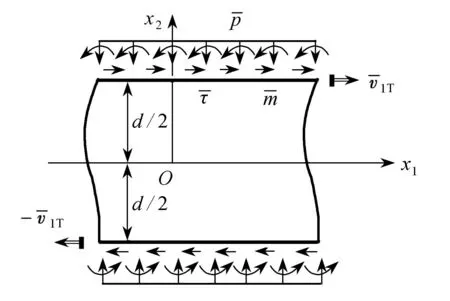
图1 剪切带脱离体及受力示意图及坐标系选取Fig. 1 Schematic diagram for the shear band with applied forces and coordinates
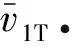
(7)
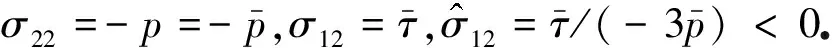
根据上述应力状态,剪切带内临界状态强度条件(5)简化为
(8)
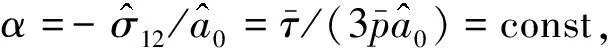
(9)
这里引入了无量纲长度因子ξ=x2/lc,并记θ′=dθ/dξ,其中
(10)
称为材料的细观特征长度,它与土体平均粒径d50呈正比,并与材料细观和宏观强度参数之比相关.
将流动法则(9)代入平衡方程(7)的第三式,可得到关于θ的控制方程(参考附录):
(11)
其中,ξd=d/lc为剪切带厚度的无量纲参数或剪切带的厚度因子;
(12)
3 剪切带临界状态完全解
上节推导表明,微极亚塑性模型所模拟颗粒土中的剪切带趋于临界状态(无剪胀流动状态)时,带内质点的Cosserat转动角速度θ满足非线性常微分方程(11).本文的主要目标是通过求解方程(11)获得剪切带厚度因子及带内各变量的分布规律.具体讨论如下.
3.1 方程的特点
本文所要求解的控制方程(11)具有以下几个主要特点:

2) 方程(11)关于基本变量θ具有齐次性, 若θ(ξ)是方程的解, 则对于任意常数A,Aθ(ξ)也是方程的解.
3) 剪切带的基本特征是其内部材料处于流动状态,外部材料作不变形的刚性运动,因此在剪切带内部θ≠0,在边界ξ=±ξd/2处应有θ=0.因此剪切带的厚度因子ξd由θ的一个完整变化周期决定,并且与θ的绝对值无关.
3.2 问题的形式解
为求解方程(11),引入如下的变量替换:
(13)
容易验证
考虑先在半带厚(0≤ξ≤ξd/2)内求解θ和其余变量,再利用对称性和反对称性获得完全解.根据图1坐标系选择及剪切带中各变量正负号规定,应有θ≤0,θ′≥0,因此有y≤0,z≥0,从而
(14)
此外,在剪切带中心和边界处分别有
ξ=0:z=0,y=-1;ξ=ξd/2:y=0,z=1.
(15)
将替换变量(13)和(14)代入式(11),问题归结为在半带厚内求解z=z(ξ),满足方程
(16)
中间变量z=z(ξ)应对式(16)直接积分获得.另一中间变量y=y(ξ)可按式(14)求出.同时,利用ξ=ξd/2处边界条件可得厚度因子表达式:
(17)
求得中间变量z(ξ)和y(ξ)后,利用流动法则(9)可求出正则化的应力和偶应力分量:
(18)
(19)

(20)
(21)
令ξ=ξd/2,可以得到剪切带中心Cosserat转动角速度与边界处剪切速率的线性关系式:
(22)
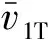
3.3 参数的确定和问题的完全解
由于未能求出式(16)的解析积分,上述剪切带中各变量的表达式仅是问题的形式解.本文中拟采用数值积分求出z~ξ关系及其余各变量的数值解.为此,需要确定方程(11)中参数β的具体数值.

(23)
根据平衡方程(7)的第三式知,(σ12-σ21)|ξ=0=(∂μ32/∂x2)|ξ=0>0.

(24)
上述分析虽然给出了参数β的范围,但尚不能确定β的具体值.通过假定r0(或β)的不同值,按数值解可求得半剪切带厚度因子ξd/2的对应值.结果表明(如图3所示),剪切带厚度因子ξd对参数r0(或β)具有强烈的依赖关系.
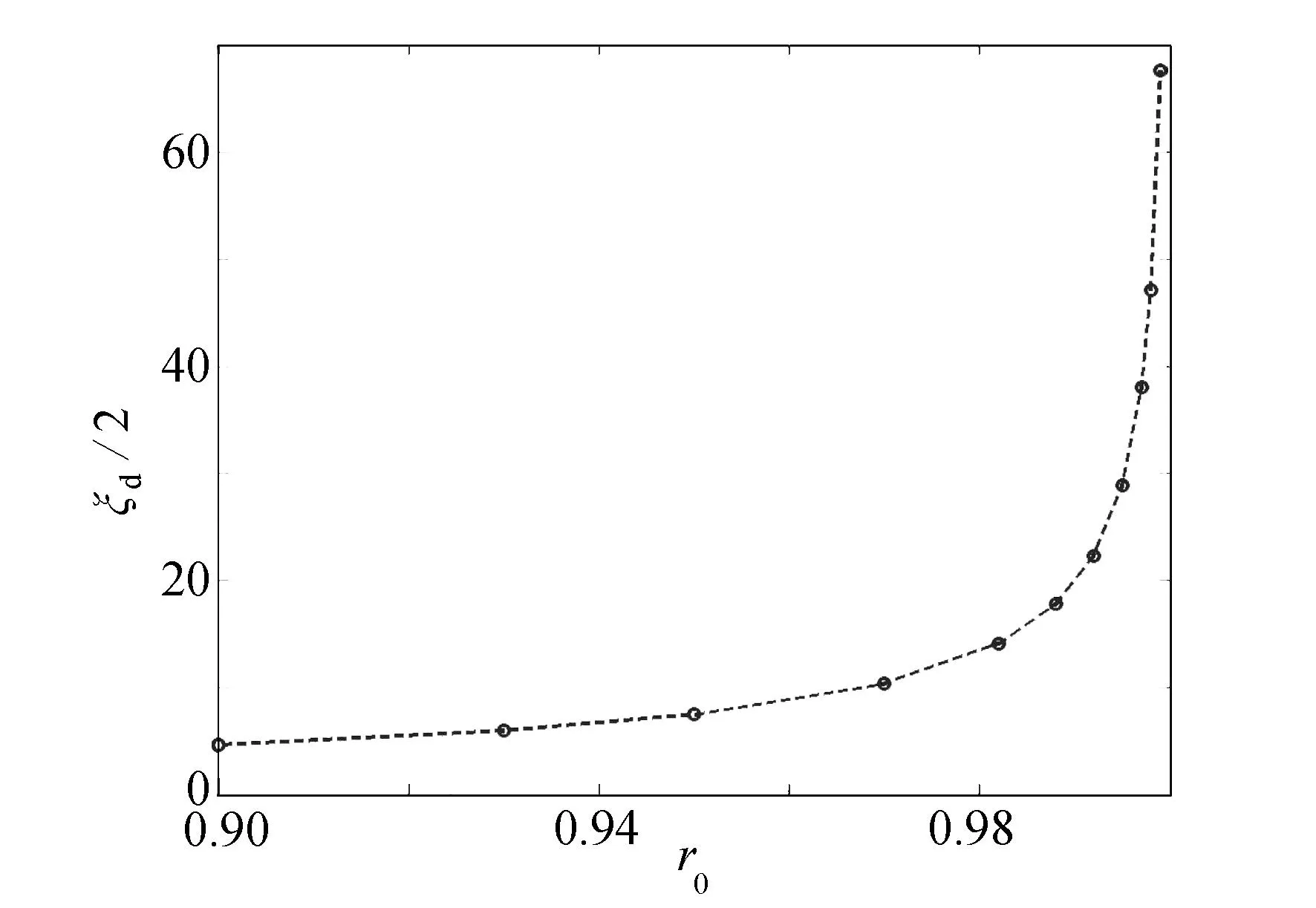
图3 剪切带厚度因子ξd/2对参数r0的依赖关系Fig. 3 Shear band thickness factor ξd/2 vs. parameter r0
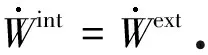
(25)
(26)
(27)
此式为假定的参数β值提供了一个后验条件.正确的结果应使β的后验值与通过设定r0得到的设定值相等,据此确定参数从而获得问题的完全解.

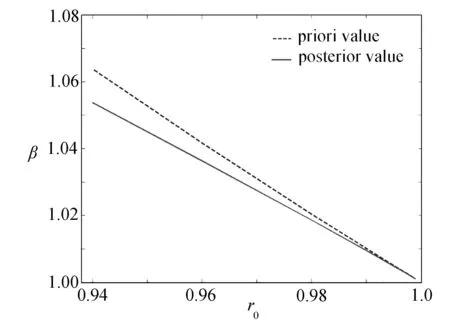
图4 对应r0设定值参数β的先验和后验值Fig. 4 Priori and posteriori values of β vs. parameter r0
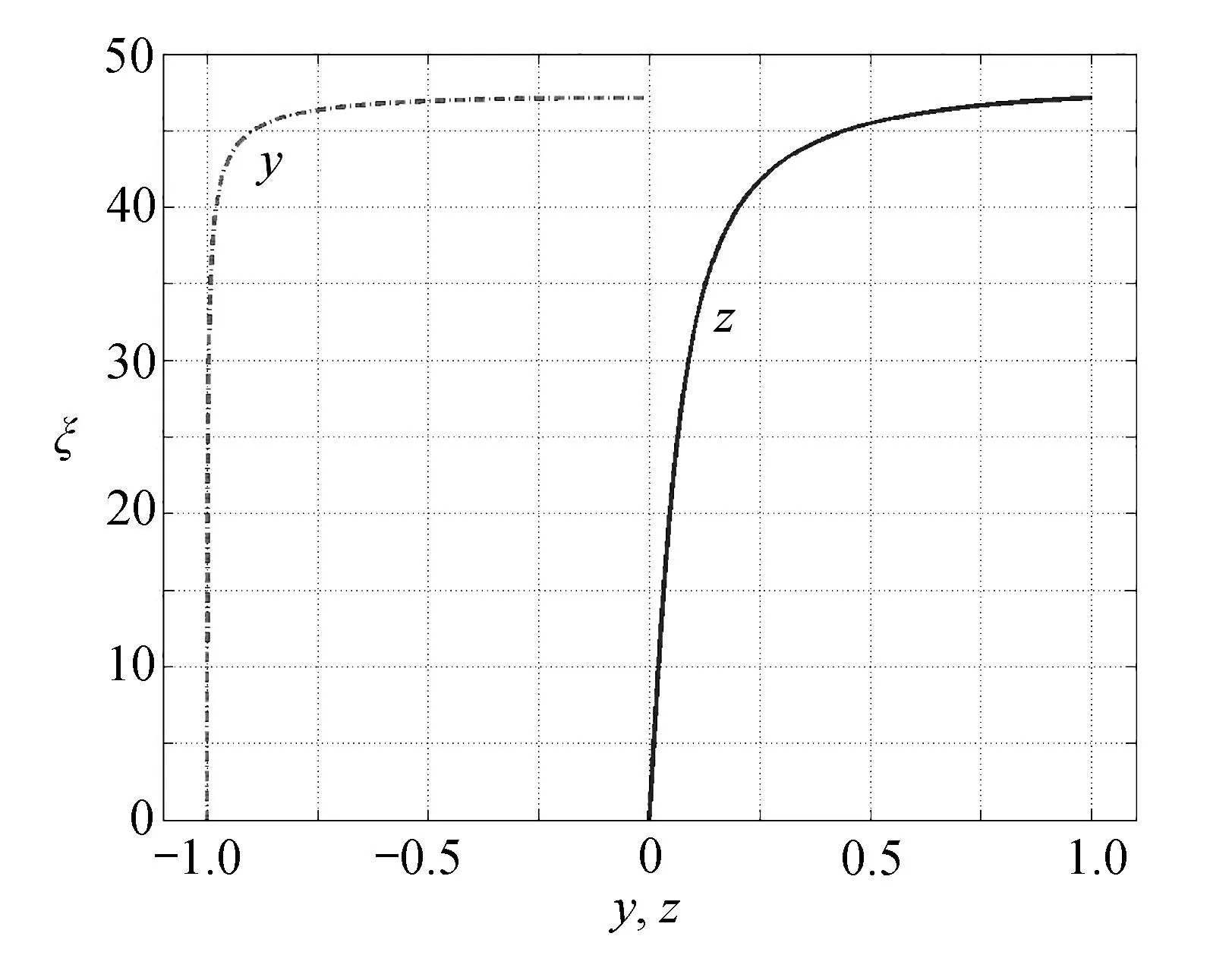
图5 半带厚内y(ξ)和z(ξ)Fig. 5 Variations of y(ξ)and z(ξ)in the half shear band
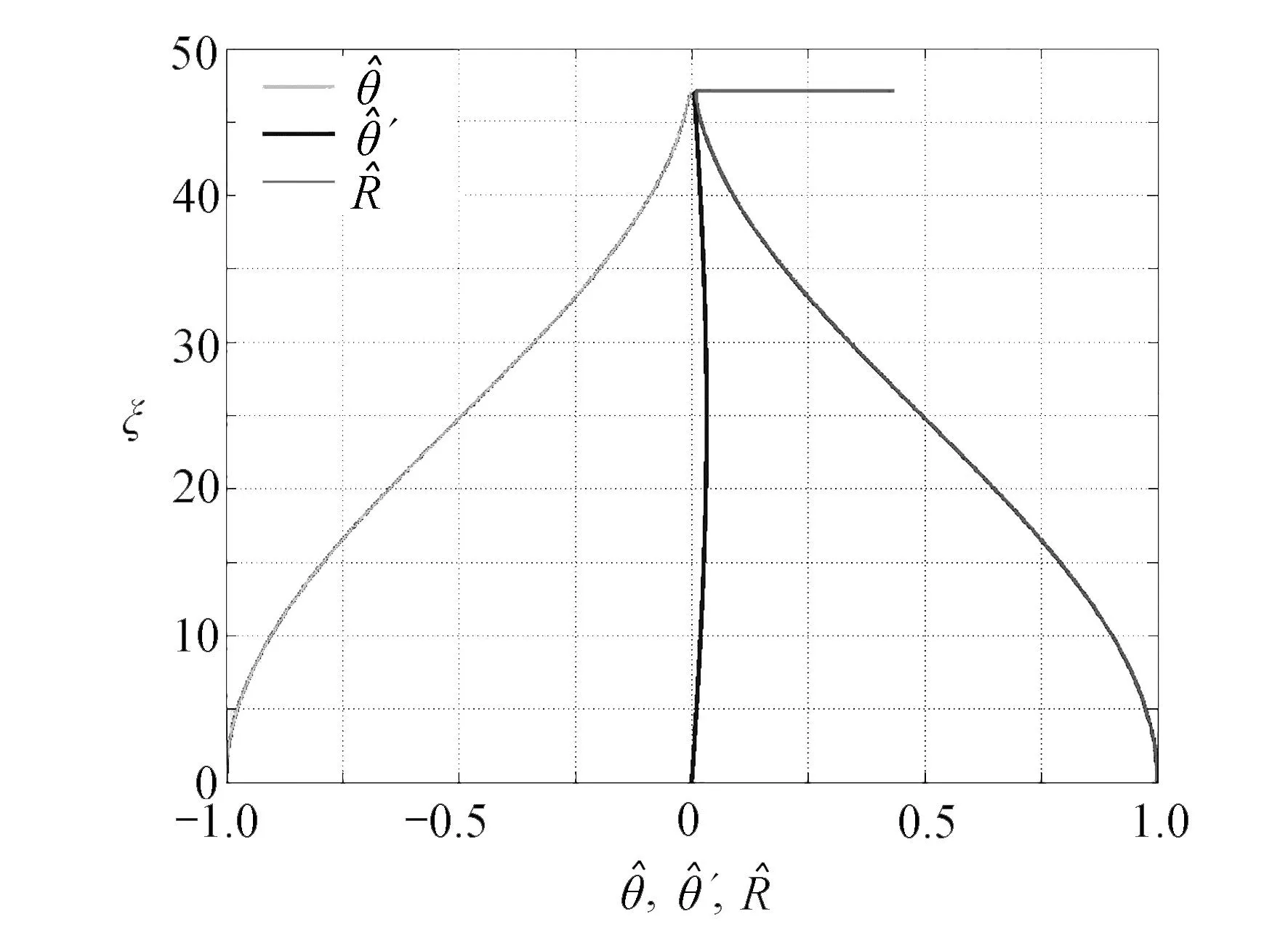
图6 半带厚内和Fig. 6 Variations of z(ξ) in the half shear band
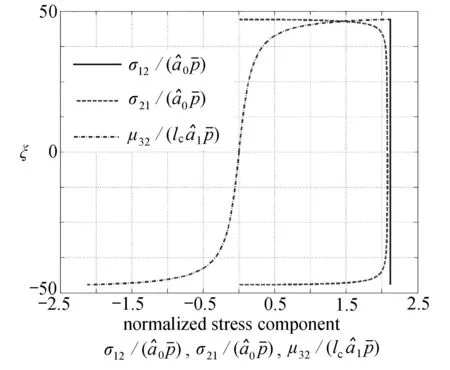
图7 剪切带内正则化应力、偶应力分布Fig. 7 Distributions of the normalized stress and the couple stress components in the shear band

图8 剪切带内正则化应变率、微曲率率和剪切速率分布Fig. 8 Distributions of the normalized strain rate, the micro-curvature rate and the shear velocity in the shear band
3.4 剪切带厚度因子的作用
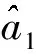
(28)

4 结 论
剪切带的厚度具有土体颗粒粒径尺度相近的量级,带内变形量的剧烈变化只有采用高阶连续介质力学模型才能恰当模拟.采用笔者[11]先期提出的微极亚塑性模型模拟的理想颗粒土,剪切带的临界状态(无剪胀流动状态)可以通过一组流动法则、强度条件和关于Cosserat转动角速度的一个非线性常微分方程描述.该方程的解析求解具有难度.笔者在本文中结合剪切带的基本特征,讨论了该微分方程的一些主要特点和关键参数的取值范围,通过应用能量守恒关系补充完备了求解条件,从而能够利用数值积分的方法求出剪切带厚度因子及带内应力、变形率各分量的分布规律等完全解.这一解答揭示了颗粒土失效时凝聚在小尺度范围内的材料剪切流动机制,而剪切带厚度因子与细观特征长度对于本构模型中细观强度参数的确定具有重要作用.此外,形如式(11)这样有趣的非线性常微分方程也值得应用数学研究者们的关注.
附录 方程(12)的推导
(A1)
(A2)
其中
(A3)
上式两边乘方后可求得R的下列表达式:
(A4)
代入式(A2)后得到关于θ的常微分方程(11).

