3D打印仿贻贝足丝结构的黏附性能*

徐万崟, 谢 宇, 钱 劲,2

(1. 浙江大学 航空航天学院 工程力学系, 杭州 310027;2. 浙江省软体机器人与智能器件研究重点实验室, 杭州 310027)

0 引 言

为了应对海洋中的波浪和激流, 贻贝会产生多个足丝, 从而通过足丝末端的黏附斑块固定在各种表面上．这种足丝线-斑块结构是一种独特的黏附器,从贻贝主体向外延伸至被黏附的物体上,通过黏附斑块与物体硬表面形成紧密的黏附[1-2],以此抵御恶劣环境带来的冲击[3-4]．每条足丝包含了三个形态不同的部分:褶皱且有弹性的近端部分、相对光滑且较硬的远端部分以及在基底表面的黏性斑块[5-6]．足丝线通常在斑块横截面中心附近的位置与斑块连接,自然状态下与横截面的夹角约为5°～45°,该角度取决于斑块位置与贻贝主体之间的距离[7-8]．

贻贝足丝具有良好的黏附性、延展性和自修复性[1,9-11],为仿生黏附研究提供了许多灵感,催生了许多新型的胶黏剂[12-15]和功能材料[16]．斑块部分与固体表面接触的界面相互作用和性能在贻贝足丝黏附中起着关键作用,而本征的界面相互作用取决于二者的理化属性[17]．本文侧重于力学研究,重点讨论了在给定本征界面相互作用的条件下,黏附结构(如足丝方向角、足丝线-斑块连接位置、斑块底部形状等关键因素)对贻贝足丝黏附性能的影响机制和调控作用,为仿贻贝人造黏附系统的结构设计和制备提供参考．研究指出[18],贻贝足丝在一定的斑-线比(足丝斑块直径/足丝线直径)范围内,存在使其黏附效率最优的结构．

本文将重点关注贻贝足丝的结构特性对于黏附性能的影响,采用3D打印技术[19-20]设计并制备了仿贻贝足丝结构,通过脱黏实验研究了其在不同方向角下的脱黏模式和黏附性能．同时,基于内聚力黏附接触理论[21]建立仿贻贝足丝结构的数值模型,以模拟仿生结构和基板的黏附作用．通过比较脱黏实验和模拟结果,分析和讨论了黏附性能的调控因素,进而对贻贝足丝黏附的调控机理有了进一步的认识．

1 仿贻贝足丝结构脱黏试样的设计和制备

在自然界中由于贻贝的种类多样,贻贝足丝的形态大小也有所差异[22-23]．本文聚焦的贻贝足丝结构源于加州贻贝[7](图1),其典型特征是足丝与基底的接触界面附近有类似蘑菇状的斑块结构[24-26],使得贻贝足丝表现出牢固而持久的黏附能力．

(a) 黏附在鱼缸上的贻贝 (b) 贻贝足丝黏附结构侧视图 (c) 从下方拍摄的斑块-玻璃黏附界面的图像(a) The representative mussels stuck to the fish tank (b) The side view image of a thread-plaque holdfast (c) The image of the plaque-glass interface taken from below to allow for direct observation of detachment process

图1(a)的比例尺为5 cm[18],图1(b)和图1(c)的比例尺均为1 mm[7]．图1(b)足丝线处于拉伸状态,外表皮上的黑色标记作为基准,用来测量试样应变;斑块底部直径约为3 mm,足丝线直径约为0.3 mm,足丝线与斑块连接处与斑块底部中心的水平距离约为0.5 mm,竖直距离(也即斑块厚度)约为0.45 mm．

为便于实验观测,本文根据上述加州贻贝足丝的形态特征,将原有尺寸放大20倍设计了仿贻贝足丝结构,如图2(a)所示．其中,lt=100 mm为试样的足丝线长度,h=9 mm为斑块厚度,Δx=10 mm为足丝线-斑块连接点与斑块中心的水平距离,D=60 mm为斑块直径,d=18 mm为足丝线-斑块连接处直径,dt=6 mm为足丝线直径．θ为试样的足丝线方向与基板的夹角,称为足丝方向角,同时作为实验中脱黏试样的加载角．在脱黏实验过程中,保持其他各参数不变,只需改变足丝线角度θ,即可分析仿贻贝足丝结构的足丝方向角θ对结构黏附性能的影响．在仿生结构的设计过程中,足丝线底部和足丝线-斑块连接处采用“放样”操作过渡连接,使试样表面形状平滑,尽可能真实地符合贻贝足丝的形态特征．

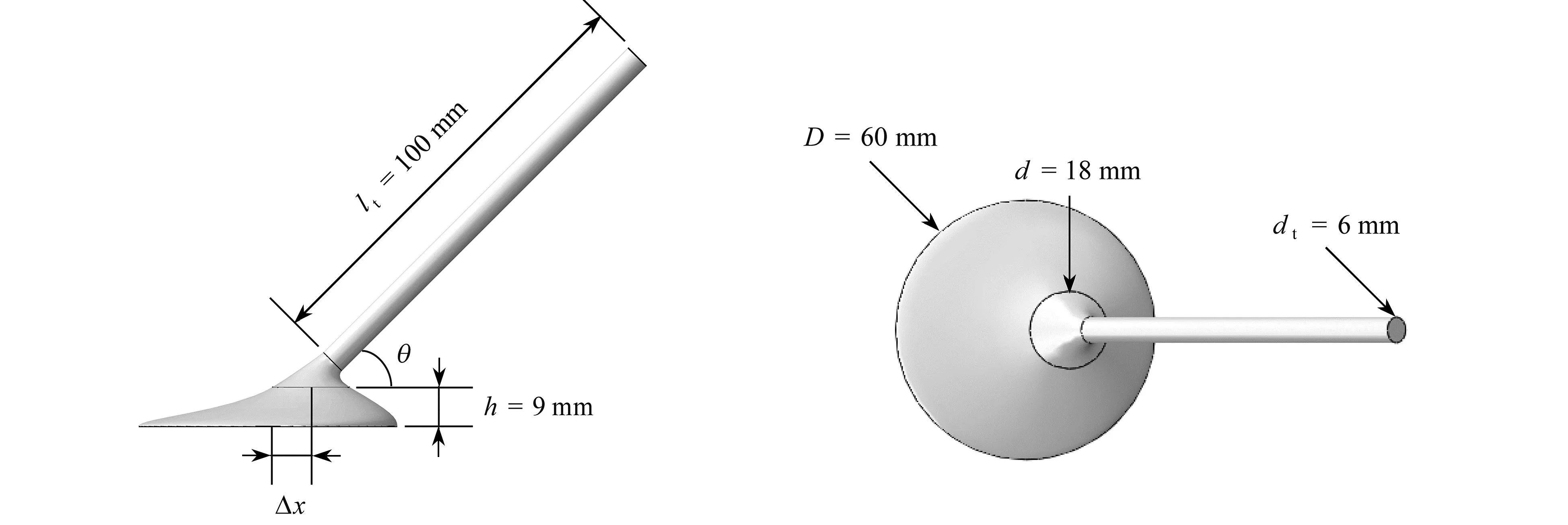
(a) 几何模型(a) The geometric model

在综合考虑自然界中贻贝足丝各部分的材质和结构特性后,我们将仿贻贝足丝结构试样分为两部分制备,如图2(b)所示:一是采用树脂材料的立体光固化成型(stereo lithography appearance,SLA)工艺[27-28]制备细长的足丝线部分;二是基于聚氨酯(PU)软胶材料的硅胶复膜工艺[29],制备了参与黏附和脱黏过程的斑块部分．所选用树脂的弹性模量为2 600 MPa, Poisson比为0.3, PU软胶的弹性模量为0.54 MPa, Poisson比为0.48．由于树脂的拉伸强度比软胶大得多,上述设计可有效避免足丝线处的破坏,从而更容易观察到试样的脱黏现象．最后,将试样的两个部分通过塑料胶连接,垂直于接触面按压一段时间后,待胶水自然风干,对连接处的缝隙以适量塑料胶加固,使其在脱黏过程中不易发生破坏．

2 仿贻贝足丝结构的脱黏实验

脱黏试样和测试基板之间的黏附层为3M5925双面胶(丙烯酸胶泡棉基材),其黏附强度适中,可清晰地呈现试样的脱黏过程而不至污染基板．我们采用聚四氟乙烯板作为试样黏附的基板,以保证试样与基板脱黏过程中不引起试样的破坏．为便于脱黏试样不同加载角(即足丝方向角)的调控,我们设计了角度可调的测试平台,并将其搭建在万能材料试验机(Instron 5944, Instron Co., Ltd., USA)上,如图3(a)所示．脱黏测试过程中,试验机始终保持竖直加载,通过转动装置的插槽来改变基板的角度,从而间接改变了试样的受力方向．

(a) 实验装置 (b) 足丝方向角为θ =45°时试样的脱黏过程(a) The experiment apparatus (b) The detachment process of the sample at a thread direction angle of θ =45°

为测试不同方向角下仿贻贝足丝结构的脱黏情况,我们制备了足丝方向角θ分别为15°,30°,45°,60°,75°,90°的仿生结构试样．在加载试样前,先剥开3M双面胶的红色离型纸,通过按压使暴露出的黏性面与试样底部均匀黏贴,之后静置0.5 h．然后,撕去双面胶的黄色离型纸,将试样轻轻放置在聚四氟乙烯基板上,随后将角度可调测试平台倒置,用装置自重对黏附体系施加压力．30 s后将装置放正,试样不再受到外界压力作用,静置2 min．之后将角度可调测试平台的基板调整至合适位置,使试样的足丝线方向为竖直方向,用夹具夹住足丝线上端,取夹持部分长度为20 mm．调零载荷和位移,启动试验机,观察并记录试样的脱黏过程,所选的拉伸速率为10 mm/min．

3 基于内聚力黏附接触的有限元模拟

为进一步研究结构特性对仿贻贝足丝结构黏附性能的影响,我们对仿生结构脱黏过程进行了有限元建模和计算．采用与脱黏实验相同的结构与数值模型,用ABAQUS有限元软件分别模拟θ=15°,30°,45°,60°,75°,90°足丝方向角下仿贻贝足丝结构的脱黏过程．由于内聚力模型可综合分析脱黏过程中界面拉伸、剪切与剥离等复杂的受力状态,因而广泛应用于研究复杂结构及其界面的黏附问题[30-31]．在数值建模的过程中,结构和基板之间的黏附作用采用内聚力接触模型,并在足丝顶端施加竖直向上的位移载荷．

为充分探究仿贻贝足丝结构的足丝线-斑块连接位置、斑块底部形状等几何特征对黏附性能的影响,并且保证有限元仿真模型的运算量和准确度,我们借助万能材料试验机测量了仿贻贝足丝、斑块的弹性模量值,所采用内聚力模型的参数来自于文献[7]中贻贝足丝界面作用的实验测试结果,如表1所示．

表1 有限元模拟所用的材料性质[7]

4 结果与讨论

我们通过脱黏实验得到了不同足丝方向角下仿贻贝足丝结构的黏附力-位移曲线,如图4(a)所示．观察不同方向角下的力-位移曲线,可以看出,这些曲线呈现出相似的变化趋势．结合θ= 45°方向角模拟的黏附力-位移曲线(图4(b))以及实验曲线(图4(c))、方向角θ= 15°时的黏附力-位移实验曲线(图4(d))、脱黏实验侧视图(图4(e))、底部脱黏区域演化(图4(f))以及对应的底部失效模拟图(图4(g)),我们归纳出仿贻贝足丝结构的脱黏过程具有4个阶段:

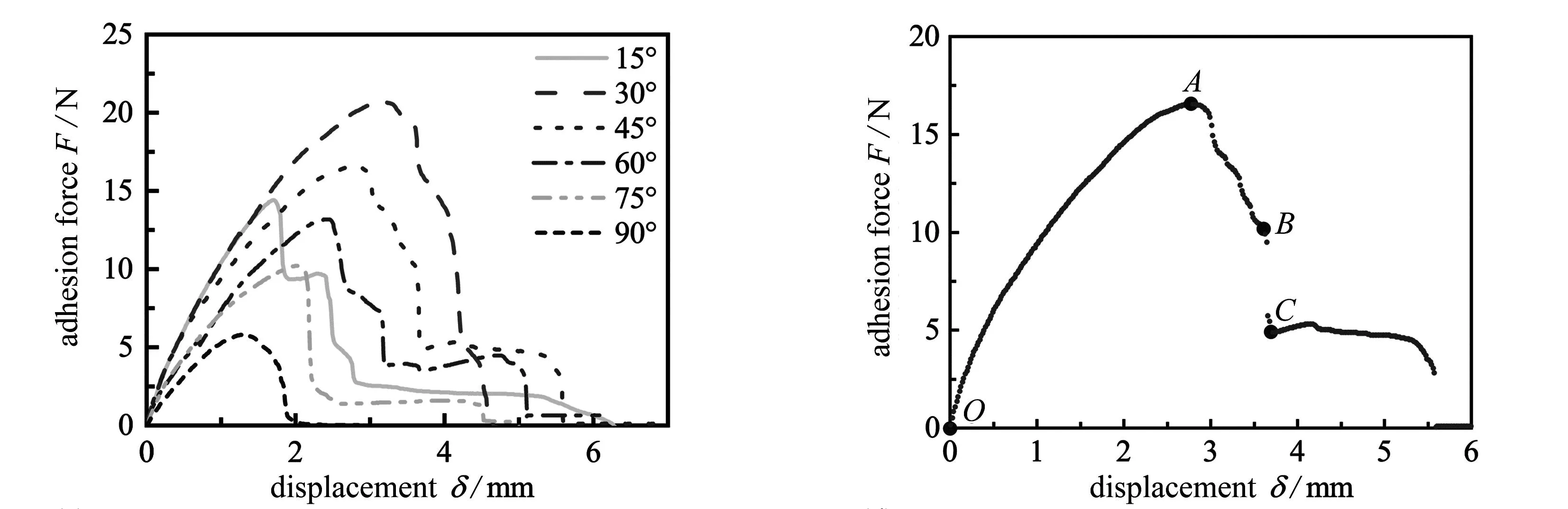
(a) 实验得到的黏附力-位移曲线(b) 实验得到的θ =45°时的黏附力-位移曲线 (a) Adhesion force-displacement curves obtained from experiments (b) The experimental adhesion force-displacement curve for θ =45°

1) 均匀拉伸阶段OA:在开始拉伸的一段时间内,黏附力随着位移的变大而增加,随着拉伸位移的增大,对应图4(g)中试样的斑块部分出现较大形变,导致整体曲线斜率逐渐降低．

2) 初始脱黏阶段AB:试样底部开始脱黏而使得受力下降,对应图4(g)中脱黏区域由中心均匀地向四周扩散,直到抵达斑块的边界．

3) 单侧脱黏阶段BC:当底部裂纹穿过边界后,对应图4(g)中脱黏区域向一侧扩散,直到该侧脱离基板,在这个过程中黏附力突然减小．

4)C点之后的完全脱黏阶段: 位移继续增大,黏附力缓慢降低,待位移达到临界状态后,拉力骤降,随后试样完全脱黏．

通过比较图4(b)、4(c)中模拟与实验的仿生结构脱黏曲线,可发现本文建立的数值模拟方法具有较佳的可靠性．此外,对于脱黏实验中底部裂纹的演化,模拟与实验的结果取得了较高的一致性．值得一提的是:模拟的力-位移曲线与实验曲线在完全脱黏阶段(力-位移曲线C点后)有一定的偏差,可能是由于仿生结构在脱黏过程中发生了较大的变形和翻转,导致与基板的实际接触面积较大,因此仍具有较高的黏附力．

由黏附力-位移曲线图4(a)可以看出,不同方向角的脱黏过程均呈现出4个阶段,但在黏附力极值以及特定的位移上存在较大的差异．为便于后续讨论,我们将脱黏的峰值力(B点)称为脱黏力,C点对应的位移称为临界脱黏位移,在C点后黏附力降为0时对应的位移称为脱黏位移．对比不同足丝方向角的仿生结构,脱黏力和临界脱黏位移表现出明显的角度依赖性,因此我们有必要探究足丝方向角对仿贻贝足丝结构的黏附性能的调控作用．

4.1 足丝方向角对黏附性能的影响

由黏附力-位移曲线与坐标轴所围的面积,可计算出仿贻贝足丝结构的黏附能．对比不同方向角脱黏的黏附能(图5(a))、脱黏力(图5(b))、临界脱黏位移(图5(d)),可归纳出: 1) 方向角为30°时实验测得的黏附能、黏附力和临界脱黏位移均最大; 2) 30°<θ<90°时,脱黏力和临界脱黏位移均随着角度的增大而减小．然而在图5(c)中,当方向角变化时,仿生结构最终的脱黏位移并没有呈现出类似的规律．

(a) 黏附能 (b) 脱黏力(a) The adhesion energy (b) The detachment force

通过实验观测和ABAQUS模拟的底部裂纹演化过程,并结合仿贻贝足丝结构的几何特性,可分析出不同方向角下仿生结构的脱黏行为．首先,我们定义斑块-基板界面上的远点和近点,如图6(a)所示:远点为界面上离足丝线-斑块连接面上圆心最远的点,即P1点;近点为界面上离足丝线-斑块连接面上圆心最近的点,即P2点．针对不同方向角下模拟的脱黏过程,如图6(b)所示,我们从中发现如下规律: 1) 方向角θ较小(θ=15°,30°)时,中间区域首先脱黏,然后裂纹前沿扩展至远点附近,再经由两侧扩展到近点附近区域;2)θ角较大(θ=45°,60°,75°,90°)时,中间区域首先脱黏,脱黏的裂纹前沿从中间区域扩展到近点附近,经由两侧扩展到远点附近区域．进一步地,观察图6(b)中不同方向角仿生结构底部的单侧脱黏状态(第三列)可得:当方向角θ=30°时,裂纹前沿在中间区域扩展的极限面积(主要黏附区域)最大,此后拉力突然减小,结构的黏附能力急剧失效,因此足丝方向角为30°时,仿贻贝足丝结构具有最好的黏附性能;而当方向角θ=90°时,裂纹前沿在中间区域扩展的极限面积最小,之后边缘快速脱黏,从而导致90°方向角下的黏附能、脱黏力和临界脱黏位移的数值较低,即黏附性能最差．实验中不同足丝方向角试样的脱黏过程如图6(c)所示,与模拟(图6(b))具有一致的脱黏过程: 1)θ角较小(θ=15°,30°)时,裂纹从中间区域开始脱黏,之后裂纹前沿扩展到远点附近,远点先于近点脱黏; 2)θ角较大(θ=45°,60°,75°,90°)时,中间区域开始脱黏,之后裂纹前沿扩展到近点附近,近点先于远点脱黏．

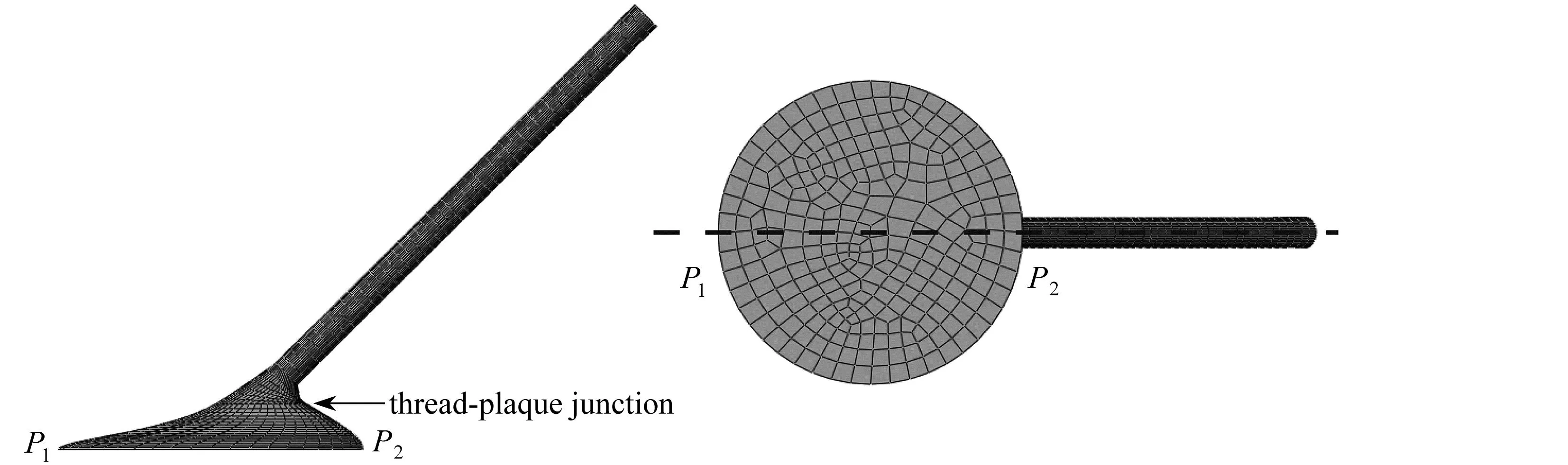
(a) 仿贻贝足丝结构的网格划分(a) The meshing of the biomimetic mussel byssal structure

从上述分析可知,仿贻贝足丝结构有最优方向角,其中最优方向角θm为30°．在最优方向角下,仿贻贝足丝结构的极限脱黏面积(如图6(b)灰色区域)占底面总面积的百分比最大．

4.2 足丝线-斑块连接位置对黏附性能的影响

依据4.1小节中脱黏时底部裂纹的演变情况,既然仿生结构初始裂纹的萌生与远点和近点有关,那进一步可推断出斑块-基板界面的足丝线-斑块连接位置可能是影响脱黏行为的重要因素．为了研究足丝线-斑块连接位置对仿贻贝足丝结构黏附性能的影响,我们通过调控足丝线-斑块连接位置中心点与斑块底面中心点的水平距离Δx(图2(a)),并用λ=Δx/R(R为斑块底面半径)来定义相对连接位置,进而模拟不同λ下结构的脱黏情况．

由图7可知,脱黏力受足丝线-斑块连接位置影响较大的是方向角θ为75°和90°的仿贻贝足丝结构．尤其是λ=0,1/6,1/3比λ=1/2时的脱黏力大得多,这表明:当相对连接位置λ≤1/3,即足丝线-斑块连接位置离斑块底部中心较近时,相对连接位置对结构的黏附性能影响不大,而当足丝线-斑块连接位置远离底部中心时,裂纹更易向边缘扩展,从而使结构的黏附能力变弱．

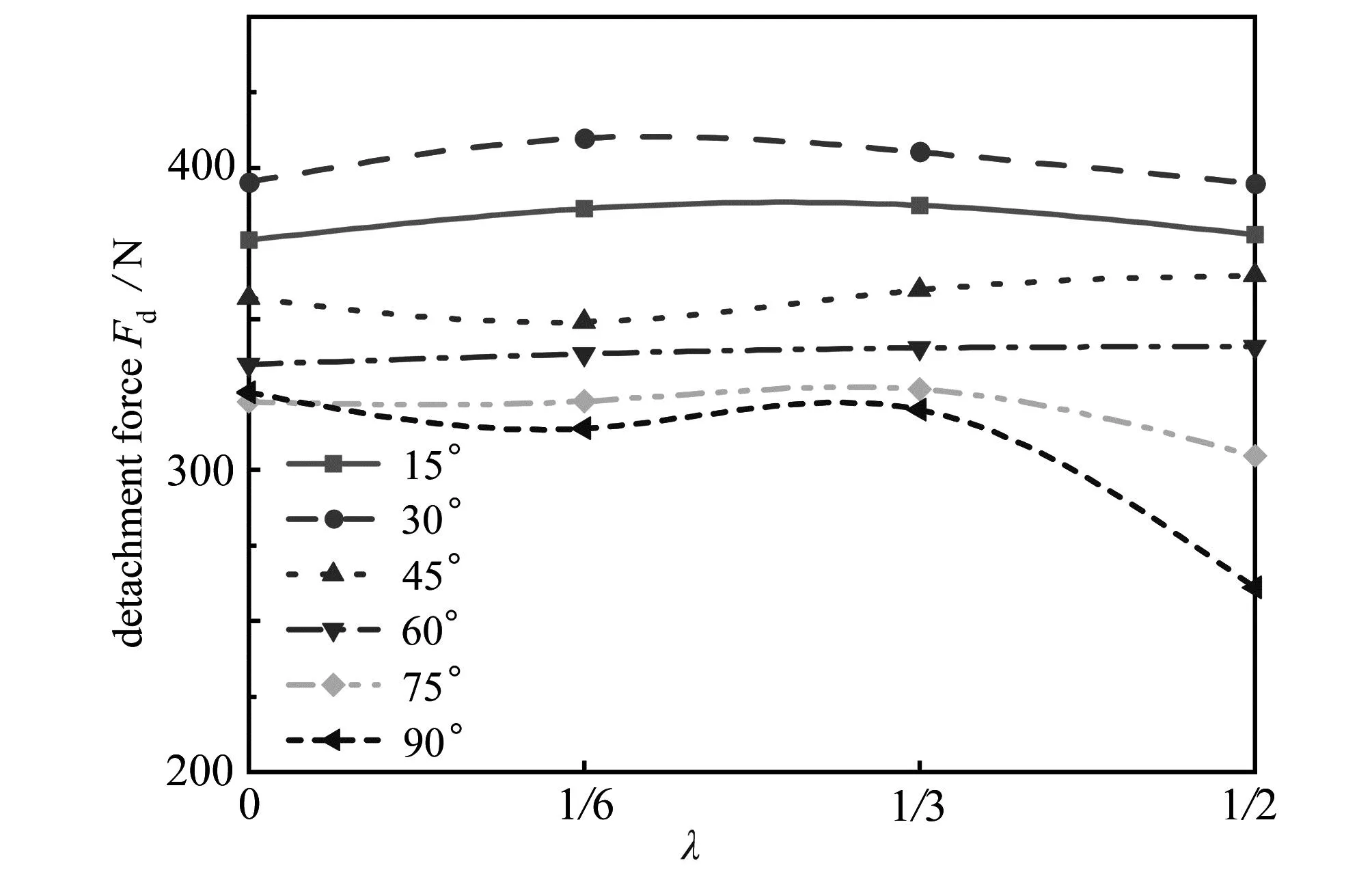
图7 不同方向角下模拟得到的脱黏力随相对连接位置的变化Fig. 7 Effects of the relative junction position on the detachment force obtained from simulations for different direction angles

然而,对于不同的方向角,仿贻贝足丝结构的黏附力与和连接位置的关系也有所差异．如图7所示,当方向角θ≤60°时,足丝线-斑块连接位置对结构黏附性能的作用并不明显,尤其是θ=60°时,脱黏力几乎不受相对连接位置的影响．

4.3 斑块底部形状对黏附性能的影响

事实上,自然界中贻贝足丝的斑块底部并不是完美的圆形,更近似于椭圆形[7,32],因此,我们在保证结构的斑块底部面积不变的情况下,在方向角θ=30°、相对连接位置λ=1/3时,改变斑块底部椭圆形的长短轴之比η=a/b(图8(a)),通过仿生结构脱黏过程的有限元仿真来讨论底部形状对黏附性能的影响．

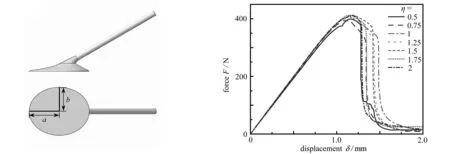
(a) 底部为椭圆形的仿贻贝足丝结构 (b) 不同长短轴之比下的脱黏曲线 (a) The biomimetic mussel byssal structure with an elliptical basal plate (b) The detachment curves for different aspect ratios

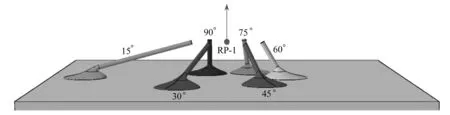
从图8(b)和8(c)中可以看出,在斑块底部面积一定的情况下,当长短轴之比η≥1时,脱黏力几乎不受斑块底部形状的影响, 黏附能在η=1.125时最大; 长短轴之比η<1时, 黏附能和脱黏力的数值都有所下降．由此,我们不难发现,当斑块底部面积一定且横向尺寸不小于纵向尺寸时,底部形状对结构脱黏几乎没有影响．该现象产生的原因是:当斑块底部面积一定且a≥b时,斑块底部的主要脱黏区域面积不变,所以结构的黏附性能几乎不变;而当斑块底部面积一定且a

5 束状仿贻贝足丝结构的脱黏过程分析

在自然界中,贻贝通常通过一束足丝黏附在周围物体上以保证本体的稳定,为了探究这一结构特性所隐含的力学机制,采用图9(a)中的束状模型来模拟仿贻贝足丝结构的脱黏过程．束状模型中包含足丝方向角分别为15°,30°,45°,60°,75°和90°的仿贻贝足丝结构,各结构足丝线的顶部平面中心围绕受力点RP-1呈圆形阵列均匀分布,且各顶部平面与受力点RP-1耦合,在该点施加竖直向上的位移载荷,模拟得到的力-位移曲线及脱黏过程如图9(b)所示．

(a) 束状仿贻贝足丝结构模型(a) The model for bundle-like biomimetic mussel byssal structures

通过模拟得到的力-位移曲线可以揭示束状结构脱黏的演化规律(图9(b)):束状足丝结构锯齿状脱黏曲线,呈现出6个极大值点,分别对应方向角贻贝仿生足丝的6个脱黏阶段．首先,当方向角θ=90°的仿生足丝开始脱黏时,束状结构整体的黏附力达到最大值,即第一个极大值(a点);然后,θ=90°仿生足丝逐渐脱黏,黏附力明显减小,同时方向角为75°的仿生足丝承受的力增加至出现脱黏,束状仿生结构整体的黏附力达到第二个极大值(b点),此时90°仿生足丝大部分已脱离基板表面;之后,θ=75°的仿生足丝逐渐脱黏,黏附力明显下降,方向角为60°的仿生足丝受力增加至出现脱黏时,束状结构整体的黏附力达到第三个极大值(c点),此时90°仿生足丝完全脱离基板;再之后,75°仿生足丝大部分脱离基板表面．重复此过程,直至所有结构完成脱黏．由此可见,方向角越高的仿贻贝足丝结构,其脱黏顺序更为优先．进一步对比不同极值附近的脱黏力位移曲线(图9(b)中的内插图),不难发现,随着束状结构逐渐脱黏,加载曲线的斜率逐步降低,而相邻两极值点间的位移量显著提高．在逐步脱黏过程中,脱黏力阶段性减小,使束状结构在出现脱黏后不至于马上完全失效,从而有效地延缓了脱黏过程,大幅提升了整个黏附体系的稳定性．

6 结 论

本文主要研究了仿贻贝足丝结构的结构因素与其黏附性能之间的关系,详细分析了仿贻贝足丝结构的足丝方向角、足丝线-斑块连接位置以及斑块底部形状对黏附性能的影响．我们利用3D打印技术制备了仿贻贝足丝结构仿贻贝足丝结构,并通过脱黏实验和有限元模拟分析了不同因素对该结构黏附性能的定量影响和力学机制,主要结论如下:

1) 方向角对仿贻贝足丝结构黏附性能有显著影响,最优方向角θm约为30°．

2) 足丝线-斑块连接位置对黏附性能的影响与方向角有关,在方向角较大(如75°和90°)时,连接位置对黏附性能的影响显著;而方向角较小(如其他角度)时,连接位置对黏附性能无较大影响．

3) 在斑块底部面积不变的前提下, 椭圆形斑块底部的长宽比对仿贻贝足丝结构的黏附性能基本没有影响．

此外,通过模拟自然界中束状足丝从平面脱黏的情形,锯齿状的脱黏曲线表明,贻贝采用的多足丝黏附结构具备强力的黏附性能,有利于其在湍急水流等恶劣环境中提高黏附的稳定性．本工作期望通过研究仿贻贝足丝结构的形状和几何因素对黏附性能的影响,推动对贻贝足丝强黏附结构的理解,为仿生黏附器的研究和发展提供新思路．未来的研究可以进一步探索仿贻贝足丝结构在不同环境下的应用,进一步完善仿生结构模型并拓展其应用领域．