基于PCA-SVM 的PSA 制氧系统关键部件故障诊断

刘健民

华氧医疗科技（大连）有限公司 （辽宁沈阳 110000）

随着我国人口老龄化程度的不断加深，居家养老人数不断增加，国内家用医疗设备市场规模不断上升，制氧系统行业的发展进入快速扩容阶段[1]。气控阀、分子筛、稳压阀等为制氧系统的关键部件，对于制氧系统的运行起着至关重要的作用[2]。制氧系统运行中常出现许多故障。朱芬梅等[3]提出运用支持向量机建立推理机自动判断实时的技术状态是否正常。刘璇斐等[4]以专家机为方法开发了用于制氧系统的故障分类诊断机，以提高制氧元件故障诊断的准确率。但分类算法诊断的关键是通过训练样本数据满足高准确率要求，然后对实际状况下收集的数据进行故障诊断分类，所以样本的选择至关重要，特征突出的样本数据可以较好地提高分类的准确率，但仅通过对模型进行更新无法达到分类准确性的要求，所以以上方法应用于制氧系统故障诊断无法保证其诊断的准确性。

基于此，提出一种基于主成分分析（principal component analysis，PCA）、支持向量机（support vector machine，SVM）的PSA 制氧系统故障诊断方法，利用PCA 降维消除特征值冗余，生成故障敏感特征，再对SVM 进行训练和测试，生成故障诊断模型实现制氧系统故障的精准、高效、全面分类。

1 PCA 主成分分析原理

PCA 采用降维思想将高维度的、相关性较大的多个指标，通过数学变换转换为数个不联系的综合指标，且转换后的综合指标一般可以表征为转换前90%以上的多个指标，即主成分[5]。

需要对矩阵X XT进行特征分解，特征值排序为：λ1≥λ2≥…≥λd，再取前d′个特征向量构成W=（w1，w2，…，Wd′），其中d′通常可以自由设定[11]。

2 支持向量机SVM 原理

SVM 是建立在 VC 维理论和结构风险最小化原理之上[12]，特别针对于解决数据样本非线型、维度高、数据样本不充分等问题[13]。

SVM 的原理核心为寻找最优超平面ωTx+b=0，当数据集呈现线型状态时，寻优问题为：

其中，ω为超平面方向，b为超平面距原点距离[14]。

当数据集呈现非线型状态时，加入松弛变量ζi>0 和惩罚因子C，可以控制最优超平面对本身的路径规划，所以式（5）成为凸二次规划问题[15]：

SVM 为解决数据特征不明显问题，通过寻找最优的核函数将1 个低维度的数据集通过升维的方式向高维空间映射，最终获得1 个函数，使数据集在低维与高维的内积结果一致，此种函数即SVM 核函数。常用的核函数有高斯核函数、多项式核函数等[16]。

引入核函数k（xi，xj） 和拉格朗日乘子αi，则式（6）变形为[17]：

SVM 模型在给定的样本集 D1 中，通过寻找最优化的ω和d确定1 个划分超平面[18]，将不同类别的样本分开，遇到复杂的样本集 D2 时，通过寻找合适的核函数g使样本集中数据升维再寻找可划分的超平面[19]，或采用惩罚因子C与松弛变量ξ来约束划分超平面[20]，达到 SVM 模型准确分类的效果。

3 PSA 制氧系统故障诊断分析

3.1 PSA 制氧系统关键部件的作用

PSA 制氧系统内最关键的3 个部件，分别为气控阀、分子筛以及稳压阀。气控阀实现分子筛的周期性进气，以及PSA 制氧系统的整体排气。分子筛可以实现对空气中氮气的吸附，使进入分子筛的空气中的氧气剥离出来。稳压阀的作用是减小储气罐流出的氧气气体压力，让最终PSA 制氧系统产生的氧气压力适合人体吸入，因此，此3 个关键部件是PSA 制氧系统平稳运行的基础，也是PSA 制氧系统内部故障率最高的3 个部件。

3.2 PSA 制氧系统故障特征值选定

单独的SVM 分类模型所采用的制氧系统特征值，通过人为选定，存在较大的干扰，故障分类准确性受到限制。而采用PCA 降维的方式，可有效解决故障诊断准确率不高以及诊断时间长的问题。对于PCA 降维方式，选定的时域特征值为最大值、最小值、均值、峰值、方差、波形因子、峰值因子、脉冲因子、裕度因子、峭度、偏度均方根，频域特征值为重心频率、均方频率、均方根频率、频率标准差、频率方差。

经过PCA 后，重新生成4 个主成分分量PC1～PC4，根据图1 主成分分量累计贡献率可知，前 4 个分量已达 95%以上，符合PCA 要求，即此4 个主成分代表16 项性能指标，4 个主成分性能指标的方差贡献率见表1。

表1 PCA 指标方差贡献（%）

图1 主成分分量累计贡献率

PCA 为主成分分析经过 PCA 对16 项特征值的降维处理，得到4 种新的故障特征值 PCA1～PCA4，4 种新型特征值可以表征该PSA 制氧系统关键部件97.71%的故障特征，解决了所选取特征值不稳定性、未正交化、重复性的问题。

如图2 所示，通过PCA 降维，综合指标保留了原始变量的重要信息，彼此间不存在相关性。4 种类型分散轮廓明显，各类型区域内的数据散落点在区域内存在相互靠拢的情况，且各类型间有较好的差异性，便于模型分类。

图2 4 种类型分散轮廓图

4 模型建立

4.1 SVM 模型的建立

SVM 模型的最终表现形式，通过对待诊断特征值数据进行隔离分类，使其聚集在各自的标签下，以此表示该类故障的发生概率。

每种运行类型选取 80 个维修返厂的PSA 制氧系统，总计320 个PSA 制氧系统。收集各自的压力信号，并将上述选取到的特征值归于各自的标签下，同时数据分为2 个部分，240 组数据作为训练集，80 组数据作为预测集，见图3、图4。

图3 SVM 训练数据结果

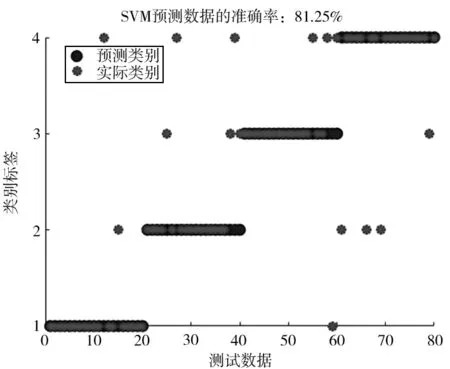
图4 SVM 预测数据结果

由图3、图4 可知，SVM 训练集的预测准确率为92.1%，测试集的预测准确率为 81.25%，不符合模型预期的准确率要求，无法在实际故障诊断中应用。

4.2 PCA-SVM 模型的建立

由SVM 模型预测结果可知，该SVM 分类模型诊断准确率过低，不适用于PSA 制氧系统关键部件的故障诊断，由此需设计一种针对PSA 制氧系统关键部件的故障诊断方法，即PCA-SVM 故障分类模型。试验数据选择320 个维修返厂的PSA 制氧系统各自的压力信号，每种运行状态下有80 组数据。数据分为2 个部分，60 组数据作为训练集，20 组数据作为预测集，结果如图5、图6 所示。

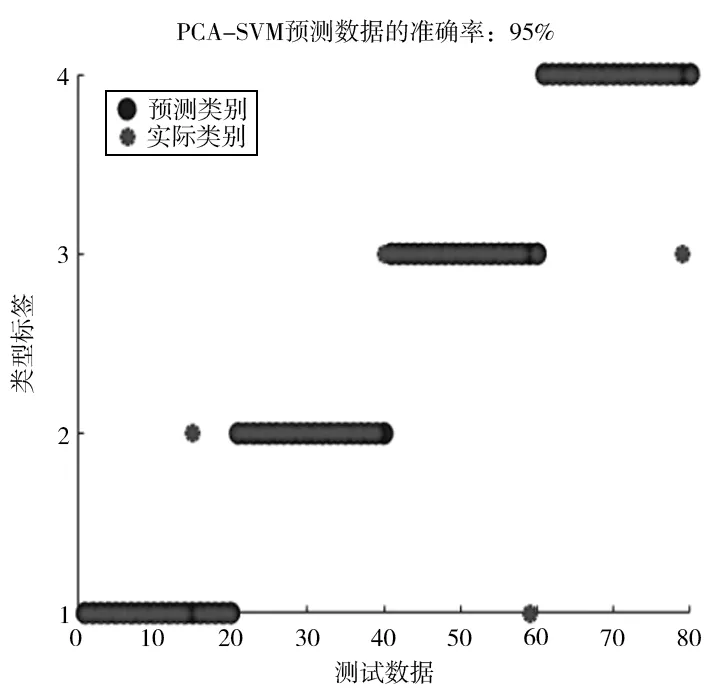
图6 PCA-SVM 预测数据结果

由图5、图6 可知，PCA-SVM 训练集的预测准确率为 100%，测试集的预测准确率为 95%，符合模型预期的准确率要求，可以在实际故障诊断中应用。

5 验证

为验证2 种模型的PSA 制氧系统故障诊断的实际适用性，选取30 个稳压阀。因市场反馈稳压阀最常见的故障为稳压阀膜片磨损，所以对稳压阀的典型故障处理为对稳压阀膜片进行手工磨损，并安装在PSA 制氧系统上进行检测，稳压阀处理结果如图7 所示。

图7 稳压阀膜片破损

采用2 种分类模型（SVM 分类模型与PCASVM 分类模型）对其进行故障诊断，故障诊断结果如图8、图9 所示。

图8 SVM 测试信号分类结果

图9 PCA-SVM 测试信号分类结果

SVM 分类模型与PCA-SVM 分类模型最终对特征数据进行归类划分，若多数特征数据归类于同一标签下，则证明此情况发生的可能性最大，应予以重视。如图8 所示，SVM 分类模型结果显示，30 组特征数据在标签“3”处的散落点数最多为80%，该模型认为标签“3”所代表的稳压阀膜片受损可能性最大，但由图8 可知，SVM 分类模型还有20%的可能性指向了分子筛故障。图9 所示的PCA-SVM 分类模型，所有特征数据点均散落在“3”号故障代表的稳压阀膜片受损故障，此种结果不会误导检测人员对PSA 制氧系统的故障判断，所以可以判定PCA-SVM 故障诊断模型更适用于PSA 制氧系统的故障诊断。

为充分验证2 种分类模型针对PSA 制氧系统的故障诊断适用性，再次选择气控阀、分子筛、稳压阀各30 个，针对3 种关键部件的典型故障进行人为破坏模拟，2 种分类模型最终准确率结果统计如图10 所示。

图10 分类模型准确率

如图10 所示，横轴代表故障类型，纵轴代表准确率，可知PCA-SVM 分类模型无论针对哪种关键部件的故障诊断准确率始终稳定在93%以上，而SVM 分类模型除正常工作情况下可以达到良好的分类结果，其他故障分类准确率仅维持在83%左右。

6 结论

本研究针对PSA 制氧系统关键部件的故障诊断难题，提出了一种准确、高效的故障诊断方法，即PCA-SVM 分类模型方法。PSA 制氧系统的压力特征值不易于提取，原因在于该系统的压力受系统内各个元器件的影响，且该系统元器件精细且复杂，所以仅通过人为分析故障特征值，并采用这些特征值对SVM 分类模型进行训练，达不到PSA 制氧系统的故障诊断准确率要求。而PCA-SVM分类诊断模型，先采取PCA 降维方式减少特征值的冗余，生成可以精确表征故障类型的特征值，再放入SVM 故障分类模型中，可提高SVM 分类模型的诊断效率与准确率。

后期的实验结果说明，PCA-SVM 分类模型相对于SVM 分类模型更适用于复杂、多变的PSA 制氧系统故障诊断，且具有全面、高效、准确率高的特点。