基于自适应陷波与重复控制的主动磁悬浮轴承系统谐波振动抑制
李俊峰,徐向波,陈 劭,王献章,付 磊,朱亚辉
(北京林业大学 工学院,北京 100083)
1 引言
主动磁轴承(Active Magnetic Bearing,AMB)是旋转机械中的一种新型支承结构。AMB 具有许多优点,如无接触,噪声小,主动可控性[1-4]。AMB 已经广泛应用于许多实际应用领域,如真空技术、涡轮分子泵和储能飞轮[5-7]。振动是旋转机械中常见的问题,AMB 刚度可控,产生主动控制力可以抑制振动。
AMB 中有两个主要的振动源:转子质量不平衡和传感器跳动,质量不平衡引起的振动力与转速的平方成正比,是旋转系统振动的主要来源[8]。当转子的惯性主轴与几何轴线不重合时,离心力将激发出与旋转频率相同的振动[9]。另一个振动源是传感器跳动,它是由转子传感表面的不均匀特性引起的,导致谐波干扰[10]。同频干扰和谐波干扰会在控制电流中引入不需要的谐波分量,从而产生传递到外壳的谐波振动力[11]。振动会降低旋转操作的质量,甚至导致AMB 系统不稳定。因此,抑制振动有助于提高AMB 系统的稳定性和精度,具有重要意义。
近年来,国内外学者抑制不平衡振动的方法主要有两种。一种是不平衡补偿,转子绕几何轴旋转,实现最小位移补偿;另一种是自动平衡控制,转子绕惯性轴或近似惯性轴旋转,使转子没有不平衡力输出[12]。针对AMB 刚性转子系统中不平衡质量引起的同频振动。Herzog[13]引入通用陷波滤波器方法,该方法在传统的陷波器环路中插入一个传递矩阵消除同频电流,并改善系统稳定性,为减少运算量,通用陷波器可转变为相移陷波器。Zheng[14]研究了陷波器连接到原始控制器上并联和串联模式下的影响,发现并联模式具有更深和更快的收敛性。Cui[15]利用X方向和Y方向位移传感器输出信号的正交特性,提出了一种基于多同频旋转坐标变换的控制算法,以抑制同频振动。这些研究主要针对自动平衡控制。为了进一步提高振动力的抑制精度,必须对同频位移刚度力进行补偿。徐[16]使用相移陷波器辨识同频位移消除同频电流,并构建前馈控制器抑制同频位移刚度力。Li[17]提出了一种双通道自适应最小均方误差算法,应用前馈校正来自适应地补偿由于质量不平衡引起的残余位移刚度。然而上述研究没有考虑传感器跳动的影响,将降低同频信号的辨识精度。
由于传感器跳动,位移传感器的输出信号会叠加多个谐波分量,并通过控制器产生电流刚度力。He[18]提出采用级联模式相移陷波器来减少AMB 控制系统谐波电流。Xu[19]采用重复控制的方法抑制了磁悬浮飞轮系统的谐波电流。文献[20]在运用频域自适应 LMS 算法抑制谐波电流的同时,还利用陷波器来消除同频振动力,最终实现了谐波振动力的有效抑制,但仅进行了仿真验证,且LMS 算法的计算量随谐波数的增加而增大。
本文提出一种复合控制方法,通过重复控制方法抑制传感器跳动引起的谐波振动,利用可变相位的自适应陷波滤波器辨识转子不平衡引起的同频信号并自适应补偿不平衡,并对同频位移刚度进行补偿,通过改变不同频率下的相位角来保持系统的稳定性,达到同时抑制质量不平衡和传感器跳动产生的谐波振动的目的。分析了所提方法的稳定性。仿真及实验结果验证了复合控制方法的有效性。
2 具有质量不平衡和传感器跳动的磁轴承转子系统动力学模型
磁轴承转子系统结构如图1 所示。两个径向平移自由度由AMB 控制。N为定子几何中心,O为转子几何中心,C为转子质量中心。以N为原点建立惯性坐标NXY。以O为原点,建立转速为Ω时的旋转坐标Oξη。坐标系的示意图如图2所示。
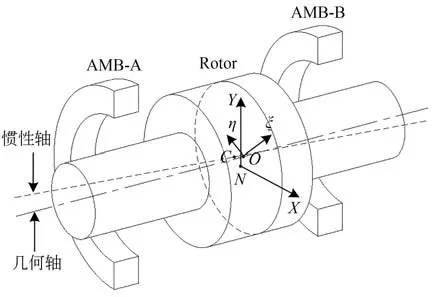
图1 AMB 转子系统结构Fig.1 Structure of an AMB rotor system
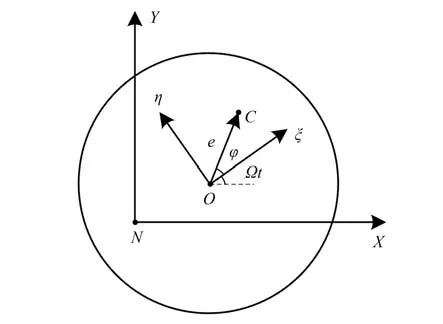
图2 坐标系示意图Fig.2 Schematic diagram of a coordinate a system
对于AMB 转子系统,转子的平移自由度沿X轴和Y轴。考虑到X和Y方向的对称性,不失一般性,转子在旋转过程中Y方向比X方向相位滞后90°,以X方向为例,根据牛顿第二定律,径向自由度运动方程可表示为:
其中:m为转子质量,fx为X方向的电磁力,fi为不平衡力。
在平衡点处,磁悬浮系统中的非线性电磁力可被线性化表示为[21]:
其中:kx和ki分别为位移刚度和电流刚度,ix为控制电流。
转子不平衡表现为转子几何中心O与质心C的不一致,以Ω的转速与转子同步旋转,使得转子不平衡引起同频扰动,不平衡力fi可以表示为:
其中:e为不平衡系数,Ω为转速,φ为不平衡质量的初始相位。
具有质量平衡的转子系统,转子质心位移为:
其中:x(t)为几何中心的位移,fd(t)表示质量不平衡引起的扰动。
受材料不均匀和位移传感器检测表面圆度误差的影响,位移传感器的输出信号会引入倍于转子转速的谐波噪声,即传感器跳动[22]。对于有传感器跳动的AMB 系统,无法获得转子几何中心的真实位置。位移传感器输出信号可表示为:
式中xsr(t)为传感器跳动,可表示为[11]:
其中:ci为传感器跳动幅度,θi为初始相位,i为谐波数(i=1,2,…,n)。
具有质量不平衡和传感器跳动的AMB 转子控制系统框图如图3 所示,其中Gc(s)为原系统的比例-积分-微分控制器,Gw(s)为功率放大器,P(s)为系统的传递函数转子系统,R(s)是参考信号。kad和ks分别是采样和位移传感器的系数。
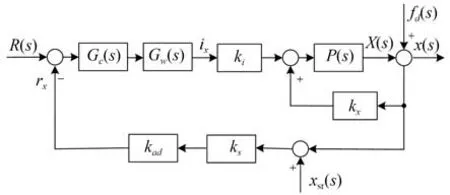
图3 具有质量不平衡和传感器跳动的AMB 转子控制系统框图Fig.3 Schematic diagram of an AMB rotor system with mass imbalance and sensor runout
根据控制框图,以fd(s)和xsr(s)为输入,ix为输出,得到如下表达式:
磁悬浮转子系统动力学方程可以公式化为:
由式(8)可知,质量不平衡引起的同频振动力包含两个部分,该振动力包含与kx相关的位移刚度力和与ki相关的同频电流刚度力,而位移传感器跳动通过传感器反馈进入系统产生谐波电流,进而产生谐波振动力。
3 抑制振动的复合控制方法
3.1 复合控制方法概述
本研究首先采用重复控制的方法来抑制由传感器和不平衡引起的谐波振动。然后,采用带相位角的自适应陷波滤波器在线提取同频信号自适应补偿不平衡,并对同频位移刚度进行补偿,通过改变不同频率下的相位角来保持系统的稳定性。
根据控制框图,为了分析方便,记Gp(s)=ki P(s)/[1-kx P(s)],Kas=kskad,干扰输入D(s)=fd(s)+xsr(s)。复合控制方法的AMB 转子系统谐波振动抑制框图如图4 所示。
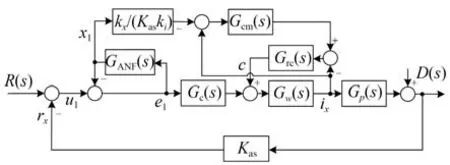
图4 采用复合方法的AMB 转子系统控制框图Fig.4 Control block diagram of an AMB rotor system with compound method
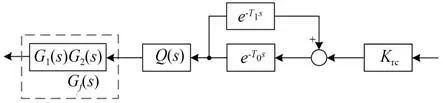
图5 重复控制器Grc(s)框图Fig.5 Block diagram of the repetition controller Grc(s)
这里Grc(s)为重复控制器,信号引入点为功放输出电流ix,插入点为功放正向控制信号,以降低功放对系统的影响。GANF(s)为自适应相移滤波器,其信号引入点为Gc(s)的输入信号,得到系统的同频信号自适应补偿不平衡。Gcm(s)为位移刚度补偿模块,对同频位移刚度进行补偿,实现同频振动力的抑制。最后通过复合控制方法实现磁悬浮转子系统谐波振动抑制。的相位特性,相位补偿器Gf(s)由两部分组成,分别采用G1(s)和G2(s)对系统的低频和中频相位进行补偿[19]。可以描述为:
重复控制器传递函数如下:
以干扰D(s)为输入,电流ix为输出,加入重复控制器后的传递函数为:
将式(10)代入式(11),整理可得:
当s=jkΩ,k=1,2,3,…,时=1,则电流ix→0。因此,该方法可以有效抑制谐波电流。
由于残余位移刚度力的存在,在上述稳定系统中引入GANF(s)辨识转子不平衡引起的同频信号自适应补偿不平衡,并对同频位移刚度进行补偿。为便于分析,定义:
GANF(s)原理框图如图6 所示,表达式为[23]:
其中:θ为保证闭环系统稳定性的相位角,ε为收敛因子,u1和u2两个信号作为输入,由位移传感器检测后获得的径向位移信号,状态变量x1和x2为输入信号u1,u2的估计值。
加入自适应陷波器后,干扰信号D(s)到输出电流ix的系统误差传递函数可表示为:
当s=jΩ,ε≠0 时,存在ix(jΩ)=0。因此,当频率与转速同频时,同频电流能被有效抑制。由式(8)可知抑制同频电流并不能完全消除同频振动力,还需进一步补偿位移刚度力。在系统稳定的基础上增加位移刚度补偿模块Gcm(s),实现同频振动力的抑制。Gcm(s)原理框图如图7 所示,其中ε1为补偿系数。
由图3 控制系统框图可知反馈进入控制器的位移rx可以表示为:
由式(3)和式(6)可知,转子不平衡引起同频扰动,传感器误差引起谐波扰动,因此有如下关系:
故反馈信号中各谐波成分可表示为:
由图4 和图7 可知:
由式(15)、式(22)、式(23)和式(24)整理可得:
由于传感器跳动带来的同频扰动叠加在转子不平衡所导致的同频位移信号中,但不产生同频位移刚度力。所以抑制谐波振动力需要将传感器跳动带来的同频扰动识别出来,使xsr(jΩ)=0,此时进入控制器的同频信号为转子的真实同频位移信号。当ε≠0 时,控制电流中各谐波成分表示为:
抑制所有谐波振动力:
3.3 复合控制方法的稳定性分析
为便于表达,定义[24]:
式(28)和Gf(s)可以分别表述为:
重复控制系统的稳定性需满足以下条件:
其中,γ由三部分组成:S0(s)产生的θa(ω),Gf(s)产生的θb(ω)和时间延迟元件eT1s产生的T1ω。且γ=θa(ω)+θb(ω)+T1ω。
加入自适应陷波器后,由式(16)可知特征方程为:
在加入重复控制器后系统稳定的前提下,特征方程可简化为:
当ε=0时,存在s=±jΩ。将ε作为自变量,s作为因变量,对式(34)在ε=0,s=jΩ处求偏导得到:
要想加入算法后的系统闭环特征函数的根都在复平面的左半平面,须满足条件:
在上述系统稳定前提下,加入同频位移刚度补偿后,系统的传递函数为:
式(37)的特征方程为:
将式(25)代入式(38)后可简化为:
当ε1=0 时,存在s=±jΩ。将ε1作为自变量,s作为因变量,对式(39)在ε1=0,s=jΩ处求偏导,得到:
要想加入算法后的系统闭环特征函数的根都在复平面的左半平面,须满足条件:
综上所述,通过选择合适的参数,使式(31)、式(32)、式(36)和式(41)同时被满足,可以保证系统的稳定性。
根据图8(a)相位补偿前曲线和参考文献[19]设计相位补偿器为:
当N1=4 时,经相位补偿后Gf(s)S0(s)eT1s相频图如图8(a)补偿后曲线所示,可以看出相位范围γ∈(139.4°,250.1°),满足式(31)相位稳定性条件。根据γ的范围,我们可以得出min|cosγ|=0.342,Kb(s)L(s)的幅频计算可以得到max {Kb(ω)L(ω)}=1.6,最后根据式(32)条件,Krc应满足:
在设计自适应陷波器相位补偿参数时,考虑了包括重复控制器在内的系统的稳定性。系统相位补偿前后的相图如图8(b)所示,为了满足式(36)中稳定条件的要求,当Ω>700 rad/s 需要相位补偿,相位补偿为170°。在设计位移刚度力补偿参数时,考虑了包括重复控制器和自适应陷波器在内的系统的稳定性,S2(s)的相频曲线如图 8(c)所示,满足式(41)的稳定性条件。
4 仿真与实验结果
为验证所提出的控制方法的有效性,使用MATLAB 进行了仿真分析,并使用高速磁悬浮电机实验平台进行了实验,实验平台如图9 所示。所提出的控制算法在基于TMS320F28377D 的控制器中实现,采样和控制频率为10 kHz。仿真和实验中使用的参数均列于表1 中。量明变。入文提方后动的波量到效制验了方的效。据流感和移感的量通式2可算动,对进FT处。

表1 磁悬浮转子系统参数Tab.1 Parameter of magnetically suspended rotor

图9 磁悬浮电机实验系统Fig.9 Experiment system of magnetically suspended rotor
图10 为转速200 Hz 时控制电流ix和振动力fx的FFT 的仿真结果,图10(a)为在没有使用振动抑制方法的情况下,电流ix的一次、三次和五次谐波分量非常明显,分别为-14.8 dB,-28.6 dB 和-33.3 dB,加入重复控制方法后,如图10(b)所示,谐波分量分别被抑制到-40.7 dB,-49.8 dB 和-53.3 dB,谐波电流得到有效抑制,振动力的一次、三次和五次谐波分量分别由-15.9 dB,-23.3 dB 和-29.1 dB 降低到-25.4 dB,-49.1 dB 和-48.5 dB,三次和五次谐波分量显著降低,但由于同频位移刚度力的存在,一次谐波分量仍然明显。加入本文所提算法后,如图10(c)所示,电流的一次谐波分量增加到-22.1 dB,但仍小于未使用振动抑制方法时一次谐波分量,增加的部分用于补偿同频位移刚度力,同时振动力的一次谐波分量显著降低,其他谐波分无显化加本所出法振力谐分得有抑,证该法有性
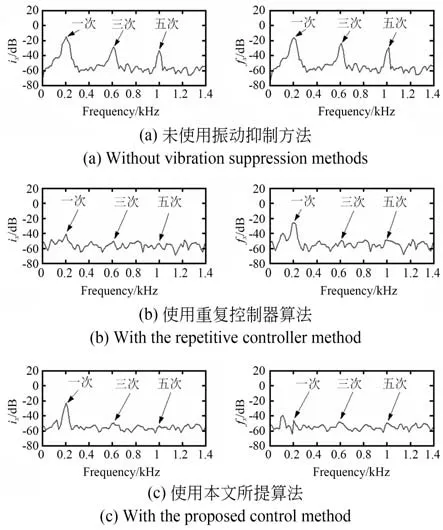
图10 转速200 Hz时算法抑制前后ix和fx的FFT仿真结果Fig.10 FFT simulation results of ix and fx before and after algorithm suppression when the speed is 200 Hz
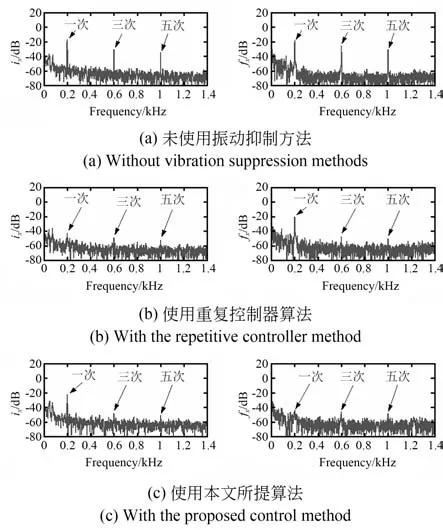
图11 转速200 Hz 时算法抑制前后ix和fx 的FFT 实验结果Fig.11 FFT experimental results of ix and fx before and after algorithm suppression when the speed is 200 Hz
根电传器位传器测,过()计振力并其行F 理图250 Hz 时进行实验,表2 为转速200 Hz 时算法抑制前后fx的FFT 实验结果,表3 为转速250 Hz 时算法抑制前后fx的FFT 实验效果。由表2 和表3实验数据对比可知,抑制效果近似一致,故仅在表3 列出了转速为250 Hz 时振动力fx的FFT 实验数据,也验证了本文所提方法的有效性。

表2 转速200 Hz 时算法抑制前后fx 的FFT 实验结果Tab.2 FFT experimental results of fx before and after algorithm suppression when the speed is 200 Hz(dB)

表3 转速250 Hz 时算法抑制前后fx 的FFT 实验结果Tab.3 FFT experimental results of fx before and after algorithm suppression when the speed is 250 Hz(dB)
5 结论
在本研究中,通过建立磁悬浮轴承转子系统模型,分析了质量不平衡和传感器跳动产生的振动机理,提出了基于重复控制和可变相位自适应陷波反馈的同频位移刚度补偿的复合控制方法,然后以X方向为例分析,设计了插入式重复控制器和可变相位自适应陷波反馈的谐波振动抑制的复合控制方法,计算了该方法的参数并分析了系统的稳定性,最后对所提出的方法进行了仿真和实验。实验结果表明:采用该算法后,一次、三次和五次谐波振动分别减少94.4%,90.4%和85.9%。谐波振动得到了有效抑制,验证了所提出的复合控制方法对谐波振动抑制的有效性。本文所提算法可应用于鼓风机、压缩机、分子泵等恒速运行的磁悬浮高速电机,也可扩展至更高的转速范围。

