双振头超声固结振动装置设计及实验

钟相强，邹令令，冯赛龙

（安徽工程大学 机械工程学院，安徽 芜湖 241000）

上世纪50 年代，人们发明了锆钛酸铅（即PZT），截至目前，常用的压电陶瓷主要有PZT-4，PZT-5 以及PZT-8，而其中PZT-4 常用在低功率的压电换能器中，PZT-5 一般不应用在压电换能器方面，PZT-8 经常被用在大功率的压电换能器中，本文夹心式压电换能器要求大功率和大振幅，故压电材料选用PZT-8［14-15］。

压电换能器的频率方程是研究超声振动的重要方程。任意阻抗下的频率方程为：

当Zω=0，即处于空载时，式（1）可以简化为：

根据设计要求，压电陶瓷晶片要与前盖板相配合，外径设为与前盖板相同的50 mm，孔内径统一设计为16 mm，厚度为5 mm。由于偶数倍的压电陶瓷晶片数量能更好地使压电换能器的前后盖板与同一极性的电极相连接，并结合实际，最终陶瓷片的数目定为p=4。压电换能器结构材料参数见表1。

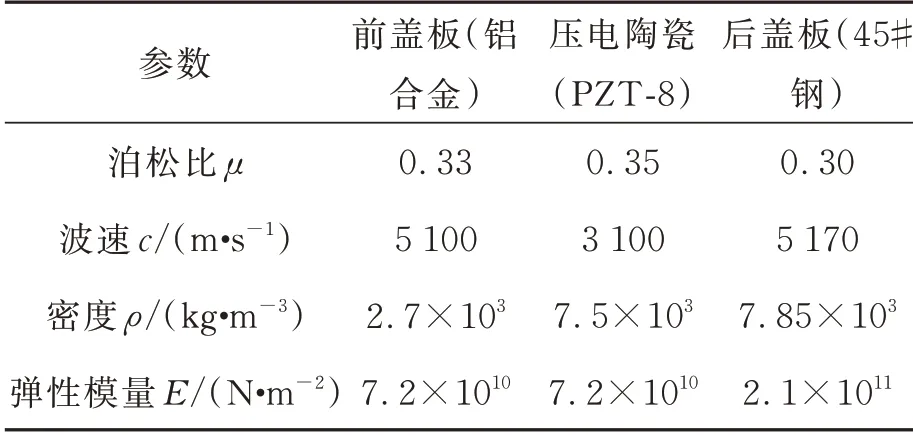
表1 压电换能器结构材料参数Tab.1 Structural material parameters of piezoelectric transducer

本文所设计的夹心式压电换能器为半波换能器，半波换能器的总长为声波波长的1/2，而所设计的前盖板长度又近似为整个压电换能器的1/2，所以该压电换能器的前盖板长度约为声波波长的1/4，即：l1=λ2/4=c2/4f=63.75 mm，四舍五入取整，长度为64 mm。

由上文可知压电陶瓷材料选择PZT-8，电极片厚度设计为1 mm，数量为4 片，则压电堆叠长度为：l=5×4+1×4=24 mm.

将所需参数代入式（2）可计算出后盖板的长度：

其中：E为弹性模量，c=为波速，ω为振动角频率，k=ω/c为圆波数。代入相关参数可得：l2=9.87 mm，四舍五入取整，长度为10 mm。

2.2 圆锥形复合变幅杆的设计

阶梯形变幅杆可以实现放大振幅的要求，但稳定性不如圆锥形变幅杆，而圆锥形变幅杆比阶梯形变幅杆的稳定性高，但放大倍数要比阶梯形变幅杆低。故本文将两种变幅杆进行结合，优势互补［16-17］。

考虑到压电换能器半径设计为25 mm，且本文固结装置单侧使用双换能器进行驱动，因此在设计变幅杆时，为了圆锥大端能和两个压电换能器尺寸相互配合且两个压电换能器之间要留有空隙，超声变幅杆圆锥部分长度初步设计为l5=66 mm，圆锥大端半径R5=55 mm，圆柱部分半径设计为R6=30 mm。

圆锥形复合变幅杆的圆波数为：

其中，c5为超声波在变幅杆（45#钢）中的传播速度，其值为5 170 m/s。

引入圆锥形复合变幅杆的频率方程和放大倍数方程分别为：

代入相关参数可得：l6=55 mm，Mp=4.69。

2.3 固结工具头的设计

目前学术界对于固结工具头的设计还没有统一的理论，只能通过工程实际来获取经验，本文设计的固结工具头是对称结构，设计的谐振频率为20 kHz，中间为固结盘作用于待固结的工件，两侧结构关于固结盘对称，材料选用45#钢，考虑到整个超声固结振动装置要相互配合，两侧圆柱直径均设计为60 mm，固结盘的直径定为75 mm。

双振头超声固结振动装置如图1 所示，压电换能器、超声变幅杆、固结工具头端面均有螺纹孔，三者之间用双头螺柱连接。将高频电信号接入到两侧的压电换能器中，输入两侧压电换能器的激励信号需设置180°的相位差，使同一时刻两侧振动方向保持一致，形成推拉作用，进而使4 个换能器产生的振幅叠加，压电换能器产生的纵向振动经由超声变幅杆放大后，传递给固结工具头，使其产生往复纵振。

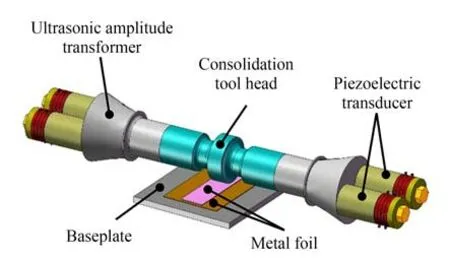
图1 双振头超声固结振动装置Fig.1 Double-head ultrasonic consolidation vibration device

3 双振头超声固结振动装置有限元分析与优化

3.1 超声固结振动装置模态分析

将压电换能器、超声变幅杆和固结工具头的三维模型导入ANSYS Workbench，在其材料栏中分别定义各元件的材料属性，然后对每个模型进行网格划分，并定义模态提取阶数为15 阶，设置搜索频率在16 000 Hz 和23 000 Hz 之间。本文模态分析处于自由模态下，即不施加外力载荷不考虑阻尼效应，最后进行模态求解。纵振状态下最佳振动频率如图2 所示。

图2 各部件的模态分析Fig.2 Modal analysis of each component

如图2（a）所示，换能器的第四阶模态为纵向振动，且其纵振频率为19 192 Hz，与理论工作频率20 000 Hz，的误差为4.04%＜5%，满足设计要求。如图2（b）所示，变幅杆的第三阶为符合加工的纵振振型，且其频率为18 688 Hz，但其与理论工作频率误差大于5%，后续将会对变幅杆的关键参数进行优化。如图2（c）所示，工具头的最佳纵振频率为20 426 Hz，与理论工作频率20 000 Hz 相差426 Hz，误差仅为2.13%＜5%，满足工程设计要求。

同理，对双振头超声固结振动装置进行模态分析，如图3 所示，该固结装置在第五阶时满足纵向振动振型，其频率为19 591 Hz，略低于20 000 Hz，但偏差低于5%，满足设计要求。

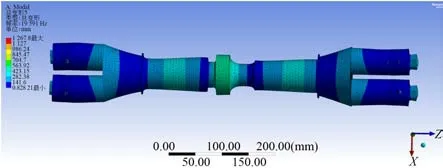
图3 双振头超声固结振动装置模态分析Fig.3 Modal analysis of double-head ultrasonic consolidation vibration device

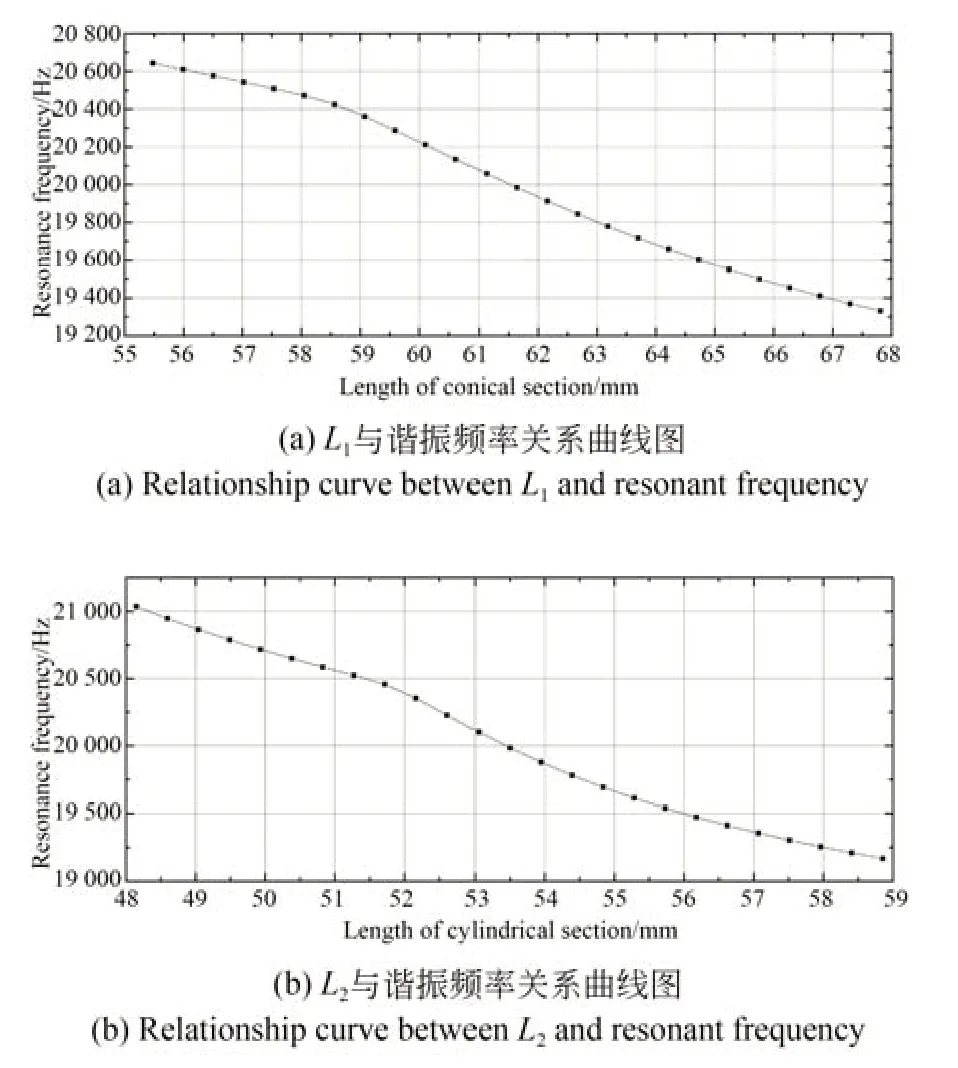
图4 变幅杆结构参数与谐振频率关系图Fig.4 Relationship between the structural parameters of the amplifying bar and the resonant frequency

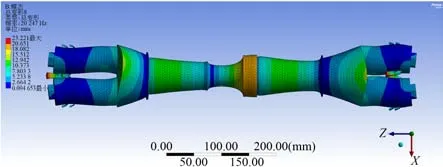
图5 优化后振动装置整体模态Fig.5 Overall mode of the optimized vibration device

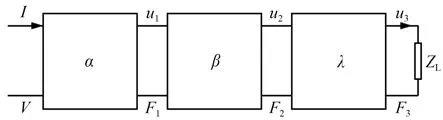
图6 换能器的机械等效四端网络级联图Fig.6 Mechanical equivalent four-terminal network cascade diagram of the transducer

3.2 超声变幅杆的结构优化

降低；L2在48～59 mm 范围内，随着L2的增大，谐振频率也在降低。

优化后的超声变幅杆圆锥与圆柱两端的直径并未发生变化，仅两端的长度发生了改变。根据优化结果，圆柱部分最优长度为53.5 mm，圆锥部分最优长度为61.6 mm，后续将会依据该尺寸制作实验样机。

4 基于Matlab 的双振头超声固结振动装置建模仿真

4.1 双振头超声固结振动装置的受力分析

故压电换能器后盖板、压电陶瓷和前盖板的等效四端网络矩阵分别为：

若换能器末端的机械负载阻抗为ZL，则：

当压电换能器处于空载状态时：

引入传输特性方程矩阵：

压电换能器后盖板、压电陶瓷和前盖板的等效四端网络矩阵可整理为：

本文工作时的功率为3 000 W，加工电压为220 V，故电流为13.64 A，联立以上方程组，代入相关参数整理得：

同理，对超声变幅杆和固结工具头分别进行受力分析，求得：

4.2 双振头超声固结振动装置的建模仿真

本文所设计的双振头超声固结振动装置由多个元件组成，其质量也具有分散性，不利于振动的分析，故通过等效质量来表示每个元件的质量，引入等效质量公式：

同理，引入等效刚度公式：

由于所设计的元件材料都具有阻尼，引入等效阻尼系数公式：

代入相关参数，对各元件的等效物理参数进行求解，结果见表2。

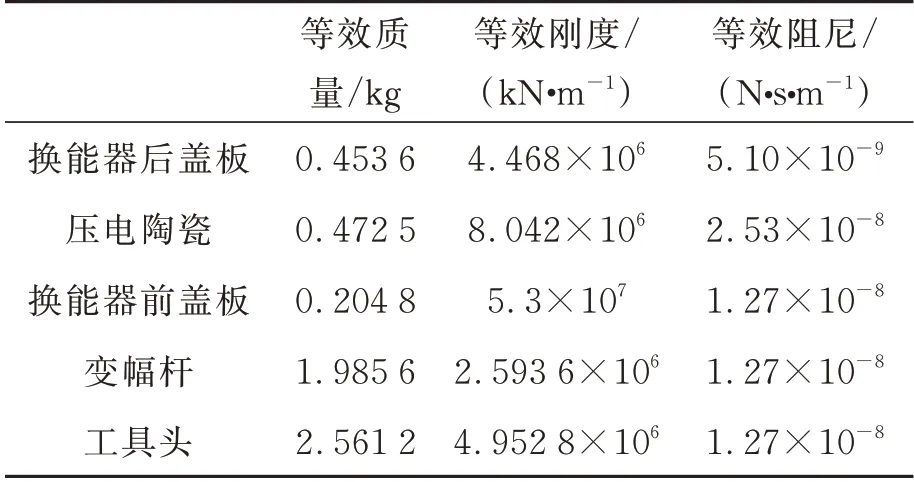
表2 等效物理参数表Tab.2 Equivalent physical parameter table

根据理论分析建立双振头超声固结振动装置半结构的五自由度力学模型，如图7 所示。其中为双换能器的激振力矩阵。运动方程为：

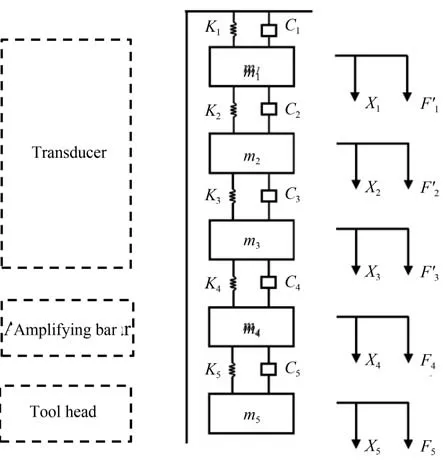
图7 双振头超声固结振动装置半结构五自由度力学模型Fig.7 Semi-structural five-degree-of-freedom mechanical model of double-head ultrasonic consolidation vibration device

根据式（14），建立双振头超声固结振动装置矩阵：

本文使用Matlab 软件对固结装置的输出振幅进行仿真分析，在Simulink 环境中，选择State-Space 模块进行模型的建立，并设置仿真所需参数，初始条件设为0。仿真完成，双振头超声固结振动装置的输出振幅仿真结果如图8 所示（彩图见期刊电子版），绿色曲线表示工具头，红色曲线表示变幅杆，黄色曲线表示前盖板，蓝色曲线表示压电陶瓷，黑色曲线表示后盖板。一个周期内，双振头超声固结振动装置的最大输出振幅为36 μm，相较于传统单侧单换能器进行驱动的固结振动装置，振幅输出值有明显提高，满足设计目标。

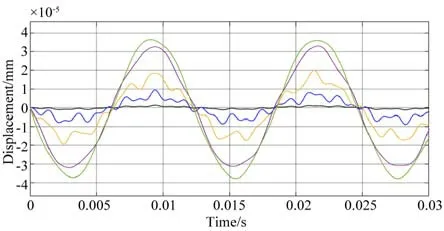
图8 双振头超声固结振动装置振幅仿真结果Fig.8 Amplitude simulation results of double-head ultrasonic consolidation vibration device

图9 振幅测试实验平台Fig.9 Amplitude test experimental platform

5 双振头超声固结振动装置实验

5.1 固结振动装置振幅测试实验

超声固结振动装置的输出振幅测试主要由扫频测试和定频测试两部分构成。扫频测试主要是为了获取超声固结振动装置的共振频率，而定频测试是为了获取共振频率下超声固结振动装置的输出振幅。对双振头超声固结振动装置进行扫频测试，结果如图10 所示。

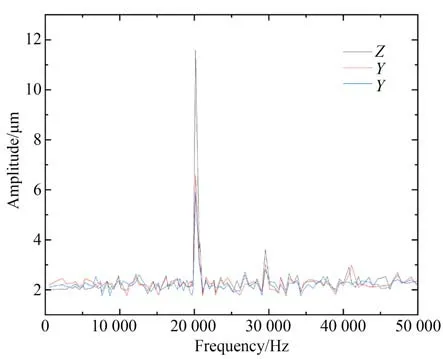
图10 扫频测试Fig.10 Sweep check

Z代表固结装置纵振时的振动变化情况，X，Y代表固结装置扭振时的振动变化情况，当频率达到20 156 Hz 时，X，Y，Z三个方向同时达到共振状态，与理论设计目标20 000 Hz 的误差为0.78%＜5%，符合工程设计要求，同时也验证了双振头超声固结振动装置结构的合理性。

对双振头超声固结振动装置进行定频测试，设置共振频率20 156 Hz，输入电压为140 V，定频测试结果如图11 所示。纵向振动状态下，双振头超声固结振动装置的最大输出振幅为34.4 μm，与4.2 节的建模仿真结果36 μm 误差为1.6 μm，误差率为4.4%，小于5%，验证了仿真结果与实验结果的一致性，达到了设计目标。Matlab 建模仿真结果和实验结果存在误差的原因：（1）建模仿真时忽略了实际工作时的环境误差；（2）实验样机加工时存在加工误差；（3）压电换能器、超声变幅杆、固结工具头及实验平台在装配过程中存在装配误差。

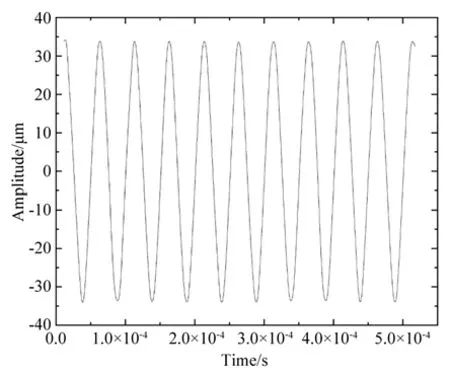
图11 定频测试Fig.11 Constant frequency test

5.2 固结振动装置输出振幅与激励电压的关系

在振幅测试实验过程中，发现超声固结振动装置的输出振幅大小与输入的激励电压信号存在一定的关系，故对输出振幅与激励电压之间的关系进行实验探究。控制信号发生器产生不同的激励电压信号，电压信号范围设置在60～140 V 之间，初始输入电压信号为60 V，之后每次递增10 V。

输出振幅与激励电压之间的关系如图12 所示，Z表示在纵振状态下，超声固结振动装置输出振幅与激励电压之间关系变化情况。由图可知，纵向振动输出振幅与激励电压呈线性相关，随着激励电压的增大，输出振幅也在逐渐增大，但当电压超过130 V 后，振幅的增速明显变慢，最终趋近于最大振幅34.4 μm。

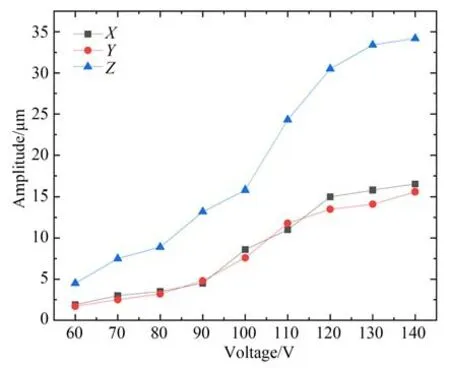
图12 输出振幅与激励电压之间的关系Fig.12 Relationship between output amplitude and excitation voltage

分析原因可知，压电换能器温度会随激励电压的增大而升高，当其温度超过居里温度的一半时，压电换能器的性能会明显下降，故振幅的增速也会放缓。

6 结论

本文针对传统超声固结振动装置输出振幅较小的问题，提出通过单侧双换能器进行驱动的方式提高固结装置的输出振幅。设计了一套双振头超声固结振动装置，基于ANSYS Workbench 对所设计的固结振动装置进行模态分析及优化，优化后的固结装置整体谐振频率为20 247 Hz。基于Matlab 平台对双振头超声固结振动装置进行建模仿真，该装置的最大输出振幅能达到36 μm。完成了振幅测试实验，纵振状态下，双振头超声固结振动装置最大输出振幅为34.4 μm，与仿真结果的误差率小于5%，验证了结构的合理性。探究了输出振幅与激励电压之间的关系，在一定的激励电压范围内，输出振幅与激励电压呈线性相关，最终趋近于最大振幅34.4 μm。该双振头超声固结振动系统结构振型正确，有效提高了系统的输出振幅，对固结效果的提升有积极意义，为后续超声固结振动系统的发展提供了新的参考，进一步促进了超声固结技术在相关领域的应用。