顾及杆状物和车道线的城市道路场景轻量化快速点云自动配准

赵辉友，吴学群，夏永华

（昆明理工大学 国土资源工程学院，云南 昆明 600093）

1 引言

随着智慧城市和数字化城市的迅猛发展，对各大场景三维信息获取的效率和精度有着更高的要求，出现了许多可以获取三维信息的方法，如傅里叶变换轮廓术（Fourier Transform Profilometry，FTP），相移测量轮廓术（Phase Shifting Profilometry，PSP），调制测量轮廓术（Modulation Measurement Profilometry，MMP），空间相位检测法（Spatial Phase Detection，SPD），锁相环轮廓法（Phase Lock Loop Profilometry，PLLP），计算莫尔轮廓术（Computer-Generated Moire Profilometry，CGMP），激光雷达距离测量等（Light Detection and Ranging Measurement，Li-DAR）［1-4］。其中FTP 和PSP 应用较为广泛，但对不同物体表面反射十分敏感，测量精度低，成像慢，效率低，对于复杂动态场景的适应还有待提高；LiDAR 是集成电子机械控制以及计算机技术等信息手段的一门新兴技术，主要通过发射和接受激光束，由于光速非常快，飞行时间非常短，因此速度快，精准，成像快。车载移动激光扫描（Mobile Laser Scanning，MLS）能够快速高效的获取大场景三维激光点云数据，具有测量精度准、视野广和效率高等优势［5］，且不受光照变化影响，能准确获得深度信息和检测周围环境。但车载MLS 在获取数据时，受扫描角度、动态目标和场景地物之间等遮挡的限制［6］，造成数据不完整，密度不均匀，需要在同一路段进行多次扫描的方式来采集数据，对区域空间信息进行缺漏补测。然而，在城市环境中卫星信号闭塞敏感，多路径效应可能导致位置误差大和较大的姿态误差积累，系统所依赖的定位精度逐渐降低［7］，同一区域重访车载点云之间存在偏差。为了整合目标场景地物完整的三维几何纹理信息，需要将多次扫描点云通过点云配准技术使其处于同一坐标系，为后续三维重建做准备。

迄今，Besl等［8］1992 年提出的迭代最近点算法（Iterative Closest Point，ICP）最为经典，但ICP 效率低，需要局部初始粗配准，否则会陷入局部最优导致配准失败。为了满足MLS 在实际工程项目的需求，许多专家和学者提出了点云配准算法相关的优化方法［9］。Gressin等［10］对点云进行划分，对每一段点云使用ICP 完成点云配准，最后合并点云实现配准；但配准误差会导致块之间出现偏差，增加误差积累，约20 cm 的精度。Lu等［11］利用旋转投影统计（Rotation Projection Statistics，RoPS）来提取关键点，并使用几何一致性方法（Sample Consensus Initial Alignment，SAC-IA）确定关键点对应关系，在户外点云上配准效果较好，在一百六十万个点配准精度3 cm；但其需要计算整体大量特征和描述，且需要的存储空间大。Yang等［12］先使用自适应距离聚类算法对点云截面进行聚类，后利用拟合线或圆柱的空间连续性来提取特征线和特征三角形，然后根据相似度进行三角形匹配，并根据几何约束拒绝不匹配的三角形。最后，该方法通过构造加权无向图的最小生成树来配准多视点云，精度达到5 cm 范围内；但对长度距离、高度和半径阈值较为敏感。Gonzále等［13］利用反射强度信息，保留反射强度高的交通标志，以交通标志为基元使用ICP 进行配准，配准精度为2 cm；但该方法对采集数据的强度特征要求较高，且强度反射距离也会造成偏差和点稀疏，影响配准精度。李鹏等［14］提出了基于虚拟特征点的拟合算法，以端点拟合、直线拟合完成点云粗配准；但却只适用于规则几何的被测物，一千万个点耗费近67 s，配准精度达到20 cm。闫利等［15］利用遗传算法进行全局搜索，寻找最优对应关系，再使用ICP 完成车载激光点云的精配准；但在局部搜索寻优花费时间较长，计算复杂度高，一千三百万点迭代了300次，花费了208 s，配准精度达到5 cm。孙培芪等［16］利用尺度不变特征转换（Scale Invariant Fea-ture Transformation，SIFT）算法提取关键特征点，后使用特征点法向量距离与其夹角进行约束，但提取特征点时间消耗长，在三万点的模型中花费了37 s，且不适用于大模型。谭舸等［17］利用激光跟踪仪来辅助实现点云配准，精度达到了1.66 mm；但只适用水平扫描固定物体，对平行地面值影响较大，且存在多站扫描误差积累，四站花费时间300 s。Li等［18］先提取杆状物，后使用蒙特卡洛定位（Monte Carlo Localization，MCL）和ICP 进行数据和地图匹配，在室外大场景数据平均绝对误差小于0.2 m；但依赖于杆状物的位置精度，且只提取了固定高度的杆状物。刘如飞等［19］提取配准基元的SIFT 关键点，应用四点全等集算法粗配准和双向KD 树改进的ICP算法精配准，完成多期道路点云的配准，配准精度在5 cm 范围；但没有考虑同名特征点的配对正确性，且存在误差积累，600 m 路段耗时近100 s。

综上，在城市场景中点云配准仍存在对噪声点敏感，提取表面几何特征少或提取不完全，配准计算复杂度较高、配准效率低和鲁棒性弱等局限性。本文根据城市道路场景中杆状物和车道线的重复性和长期稳定性，且同名特征配对准确性较高，为保证提取的准确性，利用改进方法准确提取杆状物和车道线作为目标特征，后利用改进的ICP 算法和法向量约束，将杆状物作和车道线作为配准基元，利用SAC-IA 算法剔除错误点对，并使用双向KD 树快速对应的特征点关系，降低了计算复杂度和存储占用，加快配准速度和提高精度，增强鲁棒性。

2 点云配准基本原理

本文首先得到地面点和非地面点；利用地面点反射强度值和密度分割法，将车道线根据格网灰度统计转为灰度图，通过方差阈值准确提取车道线；同时为保证杆状物的准确提取，使用RANSAC 圆柱拟合前先使用包围盒格网投影，进行遍历。后提出以杆状物和车道线特征为配准基元的面到面ICP 改进配准算法，主要使用了Levenberg-Marquardt算法进行非线性迭代优化，并引入Cauchy损失函数作为加权函数来抵抗噪声和离群点，以面的法向量和特征法向量双重约束，得到两个点云的最优配准关系，算法流程如图1所示。

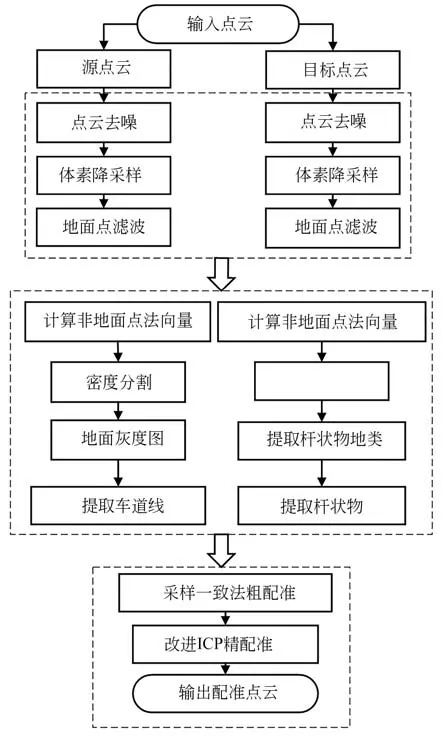
图1 本文算法流程Fig.1 Algorithm flow of this article

2.1 杆状物配准基元提取原理

杆状物在城市中属于丰富且相对稳定和规整的地物类型，具有较为显著的对象特征，比较适合作为配准的基元。杆状物的准确提取对后续配准也是重要的，为避免在提取杆状物时误将建筑物立面当作杆状对象提取，造成杆状物的误分，本文先对布料模型滤波［20］后的非地面点云使用K 均值［21］无监督分类，分类后对场景点云行道树，路灯，标识牌和电线杆打上标签，提取行道树的树干、路灯、标识牌和电线杆为杆状目标。为确保杆状物提取效果，首先对分类后的点云使用包盒法［22］建立空间格网，利用高程阈值将高于杆状物的多余点云去除；再用随机抽样一致性算法（Random Sample Consensus，RANSAC）［23］对 格网俯瞰图进行遍历，进行先验选取符合圆柱拟合的格网，并以树干为中心设置圆柱半径，对半径邻域搜索圆弧状点集；最后通过判别格网密度、最小支持点数量和垂直于立面的角度阈值，对格网内符合要求的视为杆状点云。城市路灯的灯头部会有水平延伸区域，路灯头部和标示牌的牌部点云数量较少，设置不同的密度和最小支持点云数量阈值，即可精确提取杆状点云集。

根据点云中坐标极值构建边长为L的m×n格网，将点云数据划分入规则的二维格网中，m和n计算方式如式（1）所示：

其中：Xmax，Xmin，Ymax和Ymin为点云数值极值，L为格网宽度，根据点云密度设置，本文设为1 m。

采用RANSAC 算法搜索拟合圆提取圆柱点云，设置半径缓冲区范围为0.05～0.5 m 来提取圆柱点云。

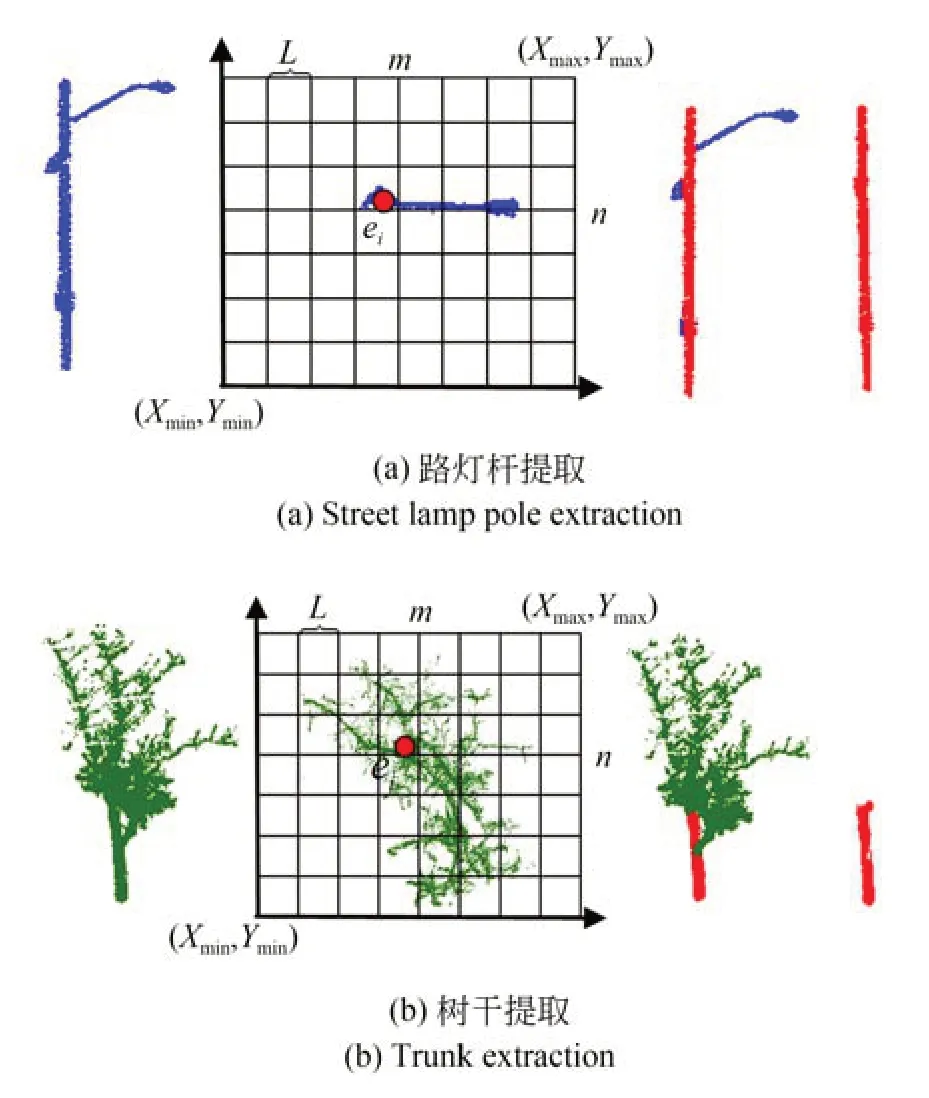
图2 树杆和路灯投影提取示意图Fig.2 Schematic diagram of tree pole and street lamp projection extraction

其中：ωR和ωM分别是路面和道路标记出现的概率；μR和μM是相应的平均水平。

网格单元灰度值计算如式（4）所示：

最后，选择最佳强度阈值：

点的空间密度定义如式（9）所示：

其中：N(p)表示点p的局部邻域，dN是邻域的大小，并且pi(xi，yi，zi)是邻域内的点。通过这样的定义，位于一点附近的点越多，该点的空间密度越高。因此，噪声的空间密度低于道路标记点的空间密度。在计算点的空间密度后，将空间密度低于阈值ρSD的点视为噪声并进一步滤除。图3 展示了强度值归一化统计图，根据车道线的强度值较小，绿色表示车道线统计；图4 展示出了在空间密度分割之后利用Otsu 的灰度格网图（彩图见期刊电子版）。

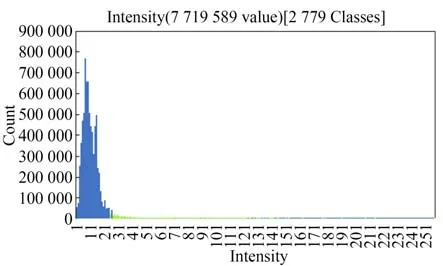
图3 密度分割反射强度统计图Fig.3 Density split reflection intensity statistical chart

图4 Otsu 提取的车道线格网灰度图Fig.4 Grayscale map of the lane line grid extracted by Otsu

2.3 L-M 改进的面到面ICP 算法

传统的ICP 算法由于采用欧氏距离最近点作为对应点，容易受到噪声干扰，会引入许多错误点对，直接用最小二乘优化计算得到的解会受一定的影响；利用奇异值分解法（SVD）［8］分解的特征值对噪声比较敏感，影响配准的精准性导致误差大。因此，本文利用概率模型构建平面到平面的距离［25］来搜索相应的点，改进的ICP 基于概率模型附加的简化步骤。保持算法的其余部分不变，降低计算的复杂度和加快配准速度，仍使用欧式距离而不是概率度量来计算对应关系。这样做是为了允许在查找最近点时使用KD 树，并因此保持ICP 相对于其他完全概率技术的主要优点，速度快和利于应用。概率函数的最小化可用最速下降法、牛顿法等方法进行非线性优化，但这些方法计算量大，收敛慢。为此，本文使用Levenberg-Marquardt（L-M）算法［26］优化的ICP 平面到平面算法进行全局精配准。不仅降低了对初始位置的要求，而且加快了配准的收敛速度。

设一个非线性方程f(x)，最基本的非线性最小二乘法，将目标函数f(x)在x附近使用泰勒公式一阶展开，得到式（10）：

其中：J(x)是f(x)关于x的导数，Δx为下降量，为使f(x)+J(x)Δx2最小，需求适合的Δx。

为目标函数Δx*展开求导并令其为0 得到式（12）：

那么可以看出是一个高斯-牛顿法的正规方程，L-M算法则在其加入一个正定对角矩阵，变为：

其中：I为单位矩阵，λ为一个正实数，用来控制步长，在每次迭代的时候，除了要更新误差函数f(x)在第k次迭代值x和在该处的一阶偏导数值以外，还要更新λ的值调节收敛步长。

其中：Τopt 为更新的刚性变换矩阵，Τ=R·t，是L-M 优化E(Τ)每次迭代求得的刚性矩阵。

为了改善相对于点到平面的性能并增加模型的对称性，使用点到面来激发概率模型。本质上，每个测量点仅提供沿着其表面法线的约束。为了构建这种模型，认为每个采样点沿其局部平面有高的协方差分布，并且在表面法线方向具有非常低的协方差。如果点的表面法线为ni，则协方差矩阵变为：

其中：α表示沿着法线的协方差的一个小的常数。这对应非常高的置信度并知道沿着法线的位置，但是不确定其在平面中的位置。

其中：si，ti为ai和bi相对应点的法向量，Rx为变换基向量的旋转矩阵。

再将式（18）和式（19）代入到式（17）计算出变换刚性矩阵Τopt。即L-M 优化的平面到平面ICP 算法构建完成。图5 提供了在极端情况下算法的效果图示（彩图见期刊电子版。在这种情况下，沿着绿色扫描的垂直部分的所有点都不正确地与红色扫描中的单个点相关联。由于曲面方向不一致，平面到平面将自动忽略这些匹配；每个对应最终求和的协方差矩阵将是各向同性的，并且相对于精确定义的对应协方差矩阵，将形成对目标函数的非常小的贡献。这种行为的另一种观点是作为每个对应的软约束。不一致的匹配允许红色扫描点沿着水平轴移动，而绿色扫描点可沿着竖直方向自由移动。因此，不正确的对应关系形成了对整体比对的非常弱且无信息的约束。

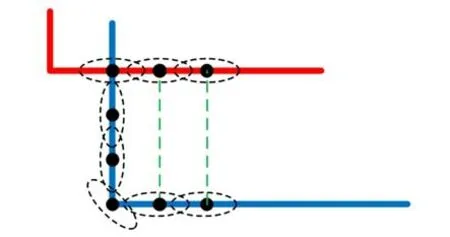
图5 平面到平面匹配示意图Fig.5 Schematic diagram of plane-to-plane matching

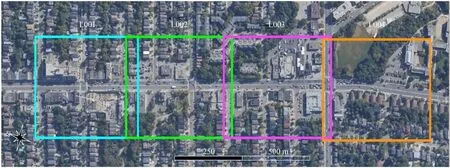
图6 研究区域示意图Fig.6 Schematic diagram of the study area

图7 L001 区域点云彩色图Fig.7 L001 area point cloud color map

为减小点云配对过程噪声和离群值的影响，利用Cauchy 损失函数［27］作为加权函数来抵抗噪声和离群点。改进的ICP 算法如下：

其中：ρCauchy为Cauchy 损失函数权重，k为损失参数，通常情况下k取1.345，r为优化时的残差。

将L-M 优化得到的Τ=R·t中的R，代入到式（19）和式（20）可以求得和，再代入求得更新变换矩阵Τopt，并求出，以此迭代使得小于设置欧式距离阈值τ或者使变换更新矩阵小于设定的阈值ς，达到其中一个条件即停止迭代。

3 实验与分析

3.1 数据准备

3.2 数据分析与预处理

依据第二节原理，本文对地面滤波过后的点云进行噪点滤除，得到去噪后的地面点和非地面点如下图，再对其分别提取出车道线和杆状物作为配准基元，更能有效快速完成配准。如图8 所示为从地面点中提取车道线流程，图8（a）中可以看出车道线与地面点的强度值不同，能看出车道线特征，但还有少量混合，为了准确提取，先进性密度分割，如图8（b）所示，看起来更加准确；图8（c）展示了根据强度值将分割的车道线转为灰度图，可以明显看出车道线，再利用Otsu 算法分割出车道线，如图8（d）所示。图9 为非地面点的杆状物提取，先将非地面点进行分类，并打上标签，如图9（b）所示；后只保留有杆状物的地类，以免建筑物立面和其他地物的干扰，如图9（c），并加快速度准确提取杆状物，图9（d）为提取的杆状物。图10 展示了提取的杆状物和车道线俯视图，红色为杆状物，白色为车道线；图11 为利用SAC-IA 进行初始估计，从图中可看出许多的同名点配对，也有误配对，但也得到了初始变换矩阵，为后续精配准做准备（彩图见期刊电子版）。

图8 车道线提取效果图Fig.8 Lane line extraction rendering

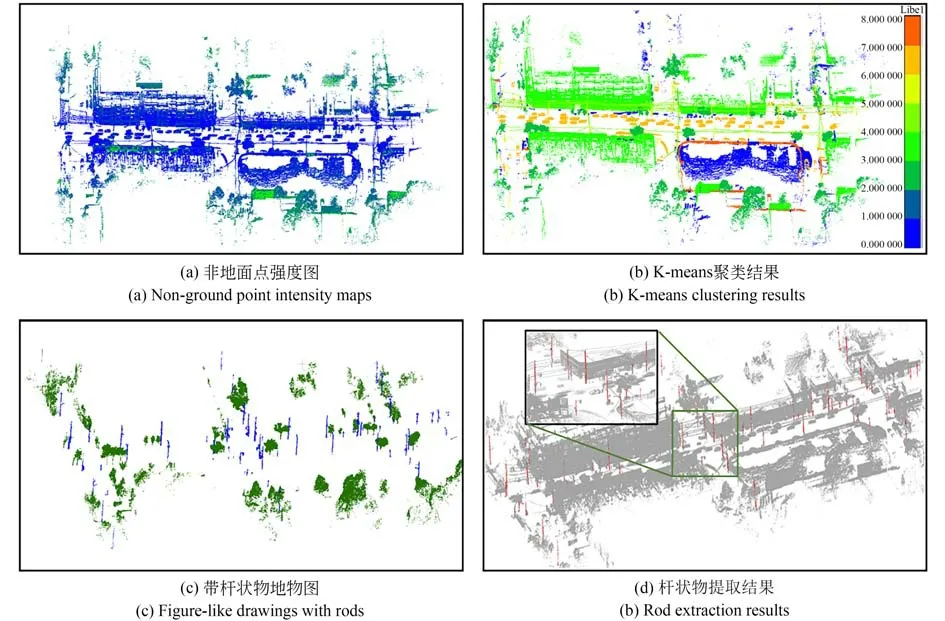
图9 杆状物提取效果图Fig.9 Pole-like extraction rendering

图10 配准基元的提取结果图Fig.10 Extraction result of registration primitives

图11 SAC-IA 算法初始估计配对Fig.11 Initial estimation pairing of SAC-IA algorithm

3.3 各算法配准对比实验与分析

实验将本文算法与点到点ICP 算法［8］、点到面PP-ICP 算法［29］、FGR 算法［30］、ISS-ICP 算法［31］和以杆状物为配准基元的ICP 算法进行试验比较。实验选择迭代次数阈值均为200 次，变换矩阵误差阈值为10-5m，均方根误差（RMSE）阈值为10-5m，满足其中一个阈值则停止迭代。本次实验的评价指标选用迭代所耗时间和配准误差［32］，采用点对的欧式距离RMSE 作为配准误差精度进行评估，单位为米。选用配准算法所耗时间作为配准效率进行评估，单位为s。由式（21）可得RMSE：

其中：si=(six，siy，siz)为源点云点的坐标，ti=(tix，tiy，tiz)为待配准点云的坐标，n为配准的点对数量。

各算法的配准结果如图12 所示，表1 时间为整体流程算法总时间，ICP、PP-ICP 和FGR 三种算法利用的全局降采样的点数量；ISS+ICP，Pole-ICP 和本文算法则是使用各自提取特征点数量，相对于ICP，PP-ICP 和FGR 三种算法数量较少，点对距离大，初始RMSE 就偏大。如图12（a）所示，将L001 区域数据利用平移和旋转分别得到不同位置的两片点云，重叠度为10%，再进行点云配准实验。结合表1 和图12 可以分析得出，点云数量较大时，传统ICP 算法配准效率低，融合效果不佳，使用邻近点对的搜索方式导致算法运算时间长，消耗了186.231 s，收敛速度慢，达到了迭代阈值次数，且对噪声较为敏感，鲁棒性较差，可从图12（b）可以看出明显位置偏差；点到面ICP 算法配准结果误差减少许多，虽然比传统ICP 算法收敛快，配准效率提高了24 s，用了162.224 s，但也达到了迭代阈值次数，从图12（c）仍可看出效果不太好，在局部放大图中依旧有明显位置偏差。FGR 算法的配准效果明显有了改善，且配准精度较高，能达到9 cm，从图12（d）可以看出基本融合，但输电线依旧可看出有偏差；由于在计算较大模型时，花费了大量时间计算快速点特征直方图（FPFH）［33］和特征描述子，配准时间较长，用了859.095 s；ISS+ICP 算法比前三种算法配准精度与效率明显提高，配准误差为0.146 85 s，但在ISS 算法提取优良点时较慢，且主要为边角点，从图12（e）主图可看出融合效果还有待提高；受到噪点的影响，后续配准收敛也慢，迭代了90 次变换矩阵才达到误差阈值，耗时51.749 s。本文方法配准结果如图 12（g）所示。从整体情况看，本文算法实现了高度融合，杆状物、车道线和其他地物配准结果较好，只花了19.622 s，比ICP，PP-ICP，FGR 和ISS-ICP 算法的配准效率分别快了166 s，142 s，830 s 和32 s，且只用了20 次迭代就达到了RMSE 误差阈值，配准精度远高于其他四种方法，达到了1.987 7×10-5m。为证明加入车道线和改进ICP 的配准提高效果，本文还与杆状物作为配准基元的点到点ICP 方法作比较。虽然多了计算车道线提取的时间，但可以明显看出本文算法迭代次数较少，且收敛较快，配准效率也略有提高，且配准精度从4.861 2×10-5m 提高到了1.987 7×10-5m，从图12（f）主图可看出比本文算法主图融合效果略差，证明了本文算法具有较强的鲁棒性。

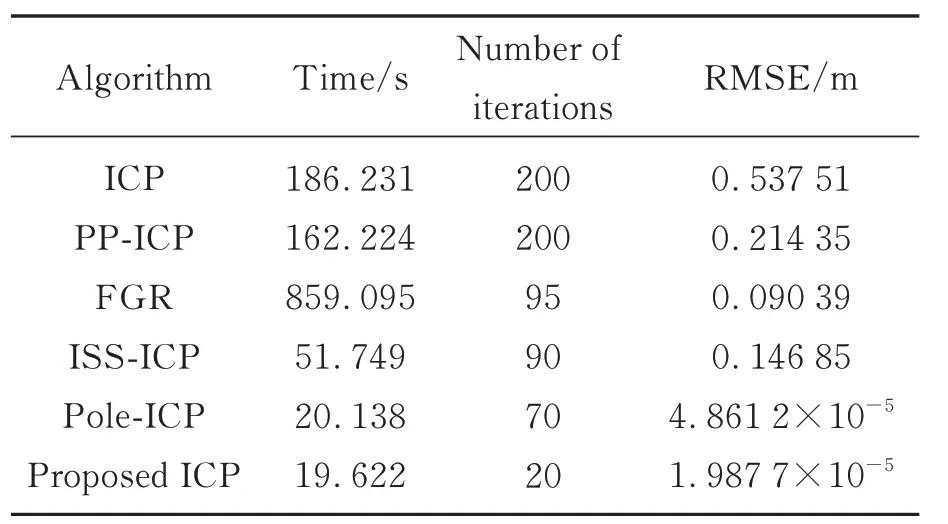
表1 各算法的配准精度和运行时间Tab.1 Registration accuracy and run time for each algorithm

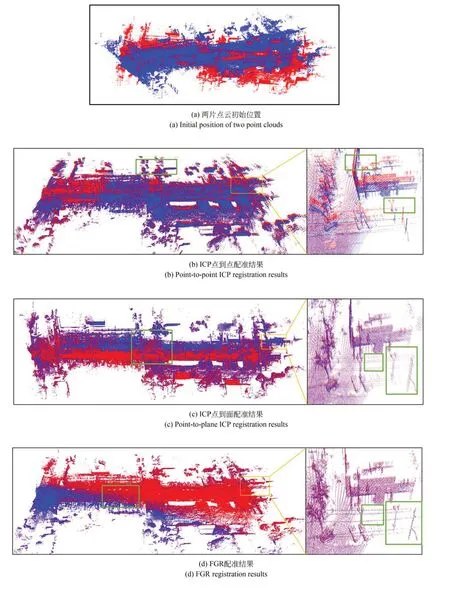
图12 不同算法的配准结果和局部放大图Fig.12 Registration results of different algorithms

图13 为六种算法的迭代收敛性对比图，初始RMSE 不一致是由于点云数量的不同。从图13中可看出本文算法收敛很快，呈现陡崖是下降收敛，Pole-ICP 算法虽然开始收敛很快，但后续陷入了局部最优，出现缓慢收敛，本文采样概率非线性优化配准，并不会陷入局部最优解，其他四种算法从图可看出收敛缓慢。

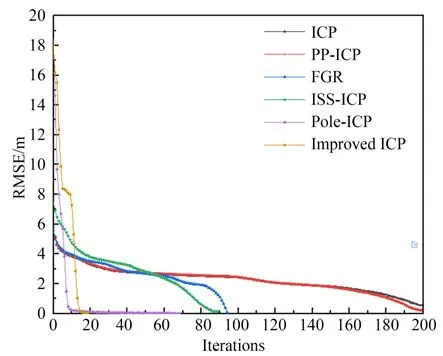
图13 六种算法收敛速度对比Fig.13 Comparison of convergence speeds of six algorithms

4 结论

针对车载MLS 获取城市场景出现不同时期位置偏差，且数据具有密度不均、目标多样和离散点多等特点，点云配准方法仍存在计算复杂度较高、配准效率低和鲁棒性弱等局限性。本文根据城市道路场景中杆状物和车道线长期优异的稳定性和重复性，提取杆状物和车道线作为配准基元。利用改进的面到面ICP 算法，并使用L-M 非线性迭代法优化和加入Cauchy 损失权重函数抗噪，利用SAC-IA 算法剔除错误点对，使用双向KD 树保证特征点对应的关系，加快配准速度和提高精度，增强稳定性。最后使用城市场景的点云数据，与五种点云配准方法进行对比实验。结果表明，在初始重叠度较低的城市环境情况下，本文配准方法相比于传统配准方法效率、配准精度和鲁棒性显著提高，在大面积点云用了不到20 秒，只需迭代20 次，精度可达1.9877×10-5米，实现了轻量化的快速准确点云配准，对三维重建具有重要意义。