弧焊机器人针对V 形坡口的焊接路径规划设计与仿真分析
刘志诚,康辉民,刘厚才,欧阳普仁,崔正杰,段良辉
(1.湖南科技大学 机电工程学院,湖南 湘潭 411100;2.江南工业集团有限公司数控加工分厂,湖南 湘潭 411207)
中厚板因其强度较大,韧性较好,被广泛应用在船体、压力容器、建筑结构等许多工程领域,但因所需面积过大不能一次性锻压成型,且板件的厚度较大,需对坡口进行多层多道焊以此来相互拼接,但多层多道焊会导致焊接变形并影响工件的尺寸精度。同时,受人工焊接效率低、工作强度大、难度高、工作环境恶劣等诸多因素的影响,亟需开发新的焊接工艺[1]。而随着现代工业机器人技术的兴起,利用机器人代替人工进行自动化焊接已成为必然的趋势[2-3],故国内外学者对此展开了比较深入的研究。如Zhang 等[4]开发了一个用户自定义的路径布局模型,以实现多层多道焊接的示教离线编程。但这种多层多道焊接路径将使得工件整体受热不均,易发生焊接变形。因此,张华军[5]通过把焊道排布由正向顺序焊接改为交叉焊接,以此来保持焊接过程中零件受热的对称性,以减少因受热不均而导致的变形。在此基础上,郑银湖等[6]通过对比正向顺序焊接、交叉焊接以及反向顺序焊接的焊道排布顺序,得出反向顺序焊接变形量最小结论。另外,在焊道截面拟合方面,传统多层多道焊道采用菱形和梯形截面拟合的方式进行摆焊[7],虽然可以减少焊道排布的数量,但相比单一的直线焊,在一定程度上使得单条焊道的热量堆积更大[8-9]。因此,胡啸等[10]在焊接菱形截面焊道时,为防止工件过热,采用非摆动焊接方式,而对梯形截面的焊道依旧采用摆动焊接方式以保证焊道的平整度。
需要指出的是,无论是摆动焊还是直线焊,其焊道设计都是采用从下往上的逐层逐道堆积,由此导致前期的焊接热量无法有效散发,大量堆积在工件下部,从而引起工件变形。针对这一问题,本文提出了一种新的V 形焊层堆积方法。即根据坡口形状,将焊道呈V 字形排布在坡壁上,以分散焊道的热量堆积,同时将空间平行轨迹和空间轮廓轨迹的特性综合应用在V 形坡口焊道轨迹的优化设计上,在规避机器人发生碰撞的同时,使每个焊层轨迹连续,且方便机器人离线编程。这样既能够有效避免传统焊接机器人因人工示教不准而导致漏焊或焊道轨迹不连续的缺陷,又能够有效减少机器人焊接时的起弧和熄弧次数,提高焊接精度和工作效率。
1 V 形坡口路径规划模型
传统面向V 形坡口的多层多道焊的填充策略是如图1a)所示的逐层逐道堆积焊接,其焊道类型依次分为打底焊、填充焊、盖面焊3 类。因其焊接轨迹由下而上且相互堆叠,致使焊接热量不能有效散发而聚集在工件底部,从而导致坡口容易发生热变形。
为了改善图1a)逐层逐道焊接时热量聚集的缺陷,根据V 形坡口的结构特点,将焊道呈V 形排布在坡壁上,从而使得焊道的热量能够得到有效散发的同时,避免了焊接热量的局部堆积,并能够有效减少工件的变形量。其焊道分布如图1b)所示。
首先根据两块板材在V 形坡口的实际尺寸和焊接强度的要求下,初始确定打底焊的高度hd[11],但为了能准确的确定图1b)中所有V 形焊层焊道的位置和焊道层数,需通过特定的等腰三角形截面对坡口截面进行划分,焊道截面的大小则由三角形的有效个数进行拟合。坡口z轴方向所能容纳的三角形层数n则为填充焊道层数nw以及焊道位置分布在做好计算的理论依据,具体计算过程如下:
因为焊道呈V 形对称分布,且在传统方式中,第2 层一般所能容纳焊道个数为两条,所以将打底焊道宽度wd的一半长度设为三角形底边长度,同时三角形高度为hd/2。此时三角形层数n为
若n不为整数,则n取小于等于本身的整数 [n]。于是,其修整过后打底焊的高度为
式中H为钢板厚度。
修整后打底焊道的宽度为
则每层V 型焊层的填充高度为
若将盖面焊层的高度等效为最顶部一层三角形。则通过除去盖面焊层(占一层)和打底焊层(占两层),填充焊层的实际层数nw为
2 V 形焊层的轨迹规划设计
在填充焊层数计算的基础上,为了实现每层焊道轨迹的连续性,避免传统焊道轨迹采用示教编程导致漏焊和轨道不准确的缺陷,需要构建每层焊道的解析表达式。为此,根据V 形坡口的截面特征,结合空间平行往复轨迹和空间轮廓偏执轨迹的可达性,对V 形焊层进行轨迹优化设计。
而在轨迹优化设计中,无论是空间平行往复轨迹还是空间轮廓偏置轨迹,一方面都需要通过V 形坡口截面的4 个轮廓点来规划截面的投影轨迹,以此作为总体轨迹规划的基础;另一方面对两种轨迹的选取,取决于板材的长度、厚度、V 形坡口的宽度等实际特征。即当V 形坡口具有深、窄、长等特征时,因机器人末端执行器在V 形截面的底部,易受空间位置的限制,其空间位姿调整极为困难,轨迹的设计需要尽可能减少机器人末端执行器的位姿调整;同时焊接过程的焊接热需要快速消散,以免热量聚集,引起零件的焊接变形。而空间轮廓偏置轨迹沿长度方向的单条焊道以及第一条焊道和第二条焊道之间的间隔时间相对较长,焊接热量能够得到有效散发,因此能满足焊接要求。而当V 形坡口具有浅、宽、短等特征时,机器人末端执行器的空间位姿调整相对方便,沿V 形截面轨迹的单条焊道轨迹耗时较长,热量能够得到充分散发,但此时坡口前后端会因长时间热量不均而导致横向变形,所以坡口总长度较短的情况下,坡口前后端的焊接时间间隔较短,故利用空间平行往复轨迹在轨道变换过程中机器人末端执行器的空间位姿调整相对简单、引入误差少、控制精度高的特点,来满足焊接精度要求。下面将介绍两种空间轨迹方程的设计过程。
2.1 轮廓点的选取及截面投影轨迹设计
如图2 所示,为确定截面投影轨迹4 个轮廓点的坐标位置,以坡口底部前端点o为坐标系原点建立工作坐标系,其中x轴沿着坡口走向,z轴此时位于坡口角平分线处。

图2 轮廓点的选取Fig.2 Selection of contour points
当焊道位于第i焊层时(2 ≤i≤nw),其投影轨迹的4个轮廓点在yoz平面上的坐标位置依次为:Pi1(yi1,zi1)、Pi2(yi2,zi2)、Pi3(yi3,zi3)、Pi4(yi4,zi4),且:
显然,Pi1、Pi2与Pi3、Pi4相对于z轴对称。
于是,截面投影轨迹的路径点从yoz平面上看,其起弧点位于Pi1,经Pi2、Pi3、Pi4这4 个轮廓点,构成第i层的截面投影轨迹。其计算公式为:
2.2 空间平行往复轨迹
若已知图1 中沿V 形坡口x轴方向的长度为L,填充焊道的高度为h′。设焊道的熔宽为w,焊道间距d=2w/3,则
式中a为x轴方向上所能容纳的焊道数。
取小于自身的整数为 [a]。则修正过后的焊道熔宽为
以焊道高度h′和熔宽w′为依据,通过二次回归线方程[12]得出对应的焊接参数,并求出修整过后的焊道截面S′。则此时焊接速度=S·Vw/S′。
进一步,以第2 层焊道为例,并结合截面投影轨迹4 个轮廓点的坐标位置和熔宽w′,可求得焊道沿x轴方向的偏移量。于是,该焊道在xoy平面的投影如图3a)所示。同时,依据焊道高度h′、熔宽w′、V 形坡口高度H、焊道层数n等参数,可求得V 形坡口空间平行往复轨迹盖面焊的关键点Pg1的坐标为而另一坐标点Pg2则关于z轴对称。此时,盖面焊道在xoy平面的投影如图3b)所示。
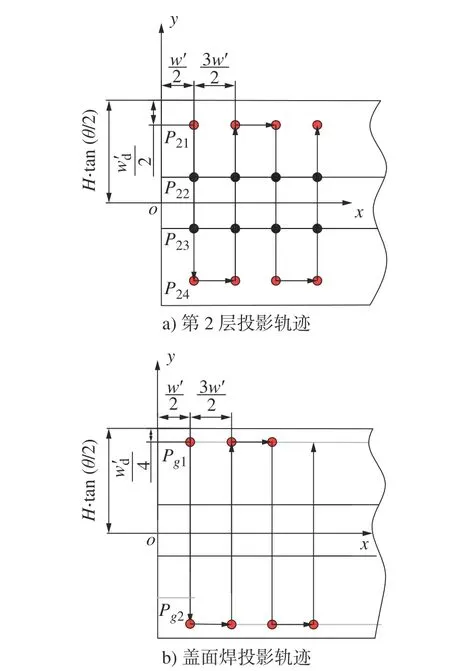
图3 空间平行往复轨迹Fig.3 Space parallel reciprocating trajectory
2.3 空间轮廓偏置轨迹
由于空间轮廓偏置轨迹相比于平行往复轨迹更加注重空间上的对称性,故在进行轨迹解析式求解时,首先将坡壁上的每条直线焊道拟合成梯形(由3 个三角形组成),如图4 中点Pij1的位置所示。
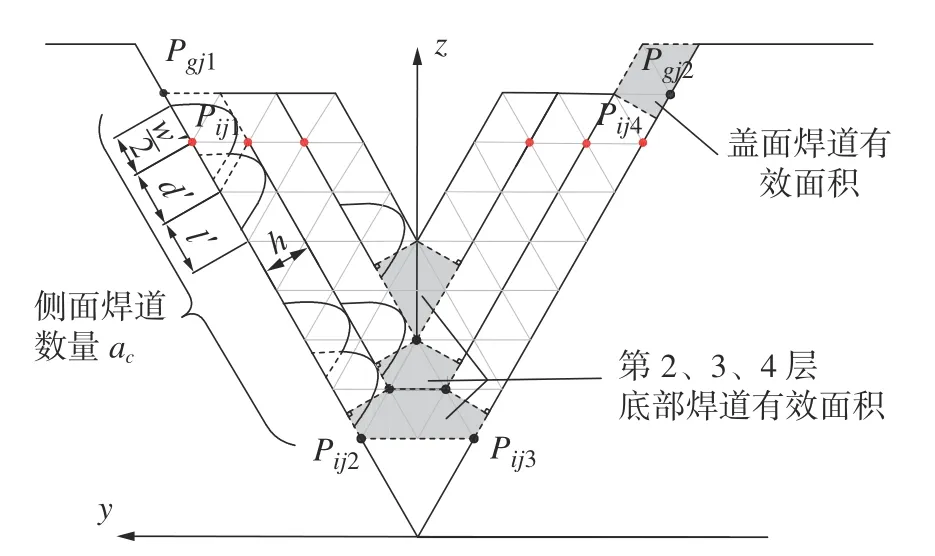
图4 空间轮廓偏置轨迹焊道排布Fig.4 Weld bead layout of spatial contour offset trajectory
再结合焊道层数n,可得出每层侧壁所能容纳的焊道圈数ac为
需要指出的是,由于单条焊道实际所占有效面积为2 个三角形,且第2、3层焊层底部的有效面积如图4 中的虚线框出,则第2、3层底部分别可容纳2、1 条直线焊道。现以第2层焊道轨迹为例。根据图2 可知:截面投影轨迹有4个轮廓点,其中靠近坡口顶部的两点为转折点,靠近底部的两点为过渡点。则图5a)中每圈轮廓的轨迹由两个过渡点的中点oij为起点,顺时针依次经过Pij2、Pij1、其中第j圈的pij1相对第一圈的偏移距离为:Δxj=2(j-1)w′/3,由此可求出侧边焊道最末圈过渡点的坐标为:piac2(xiac2,yiac2,ziac2),piac3(xiac3,yiac3,ziac3),以及对应的偏移点。则每层的底部焊道起点坐标为填充长度为
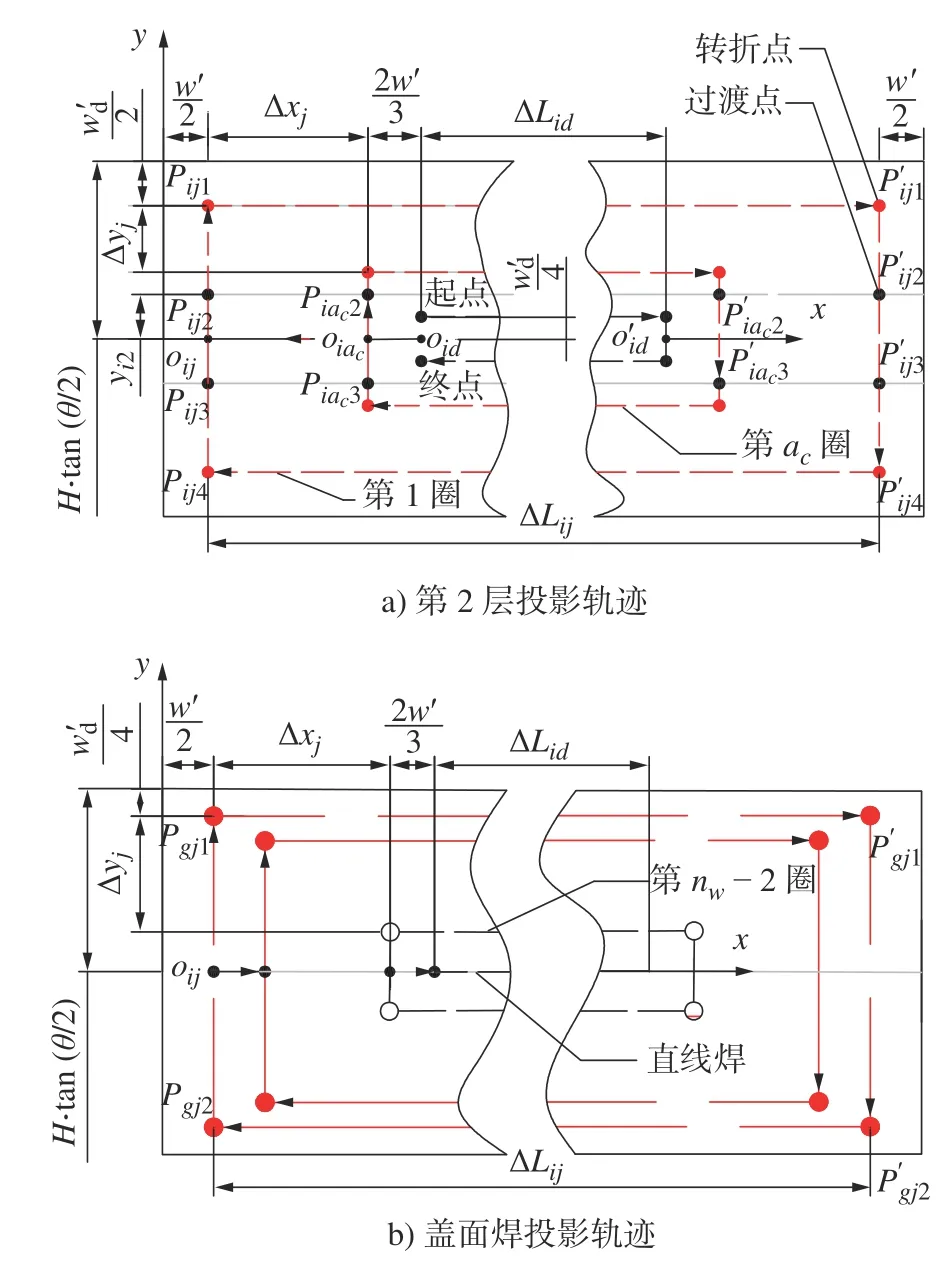
图5 空间轮廓偏置轨迹Fig.5 Spatial contour offset trajectory
通过填充长度ΔLid,可得到偏移点oid。但由于第2层底部需要两道直线焊,所以需从oid的左侧为起点,右侧为终点进行直线焊。
而对于第3层以上的所有焊层,此时两个过渡点重合,焊层底端有效面积为3 个三角形,如图4 中第4 层焊层底部虚线框出,且有效面积是单条焊道的3/2倍,此时底端焊接速度,可以利用式(15)得到由到oid的直线焊,再由空间轮廓偏置轨迹填补整个焊层。
对于盖面层焊接轨迹,同样采用平面轮廓偏置轨迹的方法进行焊接。由于之前焊层有部分缺失,所以为了能够填满坡口,盖面焊道的有效面积得设为2.5 个三角形,如图4 中Pgj2的位置虚线框出,此时盖面焊的焊接速度。为求解盖面焊的轮廓轨迹,当已知的坐标时,根据z轴的对称性可以求出其对称点pgj2,其中pgji表示盖面焊第j圈的第i点。盖面焊每圈的pgj1相比pg11的偏移量为: Δxj=2(j-1)w′/3,Δyj=。偏移距离ΔLij如式(13)所示,可求出pgj1,pgj2沿着x轴的偏移点。若n为偶数,则焊接圈数为nw-1圈。若n为奇数,则焊接圈数为nw-2圈,同时外加一条直线焊,图5b)中所示为当n为奇数时的盖面焊轮廓偏置轨迹。
2.4 三角形层数n 的奇偶性分析
无论是哪种填充焊轨迹,由于三角形层数n的奇偶特性关系,为了提高焊接效果,填充焊层的第nw、nw-1层的焊接路径需做些许的改动:
1) 若n为奇数,第nw层的焊道截面一定为高,宽的大三角形,如图6a)所示,轮廓点由pnw1,pnw2(pnw3),pnw4这3 点组成,无论是对于空间平行往复轨迹还是空间轮廓偏置轨迹,都可直接采用直线焊填补,并通过调整焊接速度,使与前焊层底端焊接速度一致即可,该层起弧点为pnw2(pnw3)。

图6 n 的奇偶性分析示意图Fig.6 The parity analysis of n
2) 若n为偶数,如图6b)中的左图所示。其中第nw层的焊道截面为高,宽的小三角形,且与第nw-1层截面组合成高,宽的大三角形。但在实际焊接过程中,为了达到焊接效果,可通过拓宽第nw层焊道为等腰梯形,如图6b)右图所示。此时,第nw层路径改为平面摆焊,摆焊起弧点为(0,0,znw1),焊枪摆幅为R=-m,m为考虑熔池形状的修正因子,一般为2 ~ 3 mm。而此时对于第nw-1层,与当n为奇数时的第nw层焊接操作一致。
综上所述,空间轮廓偏置轨迹相比于空间平行往复轨迹而言,不仅在焊接坡口时能左右对称,同时也能兼顾工件上下以及前后的受热对称,以此解决空间平行往复导致的横向变形。因此,空间轮廓偏置轨迹相对空间平行往复轨迹更加适用于坡口较深,板件较厚的情况。
但在实际工业焊接轨迹中,为避免多段直线连接处尖角所导致的突变和冲击,两种轨迹都可选择B 样条曲线或圆弧曲线等进行圆滑过渡[15],轨迹优化后如图7 所示。
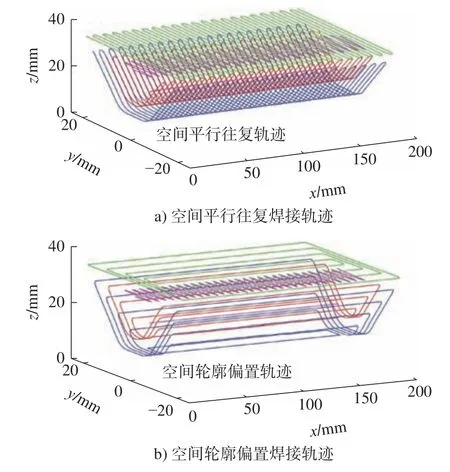
图7 总体焊接轨迹Fig.7 Overall welding trajectory
3 焊枪倾角规划
在焊道填充中,由于坡口底部的焊道深度大、空间较小、可达性较差。所以在轨迹规划时,为了避免频繁的计算焊枪倾角,通过对极端情况下的焊枪姿态进行约束,来避免焊枪发生碰触,具体设计过程如下:
如图8 中第2、3 层焊道底端的极端位置所示,图中深蓝色线为已焊的焊道外轮廓线lb, 红色线为焊炬的外轮廓线lr。
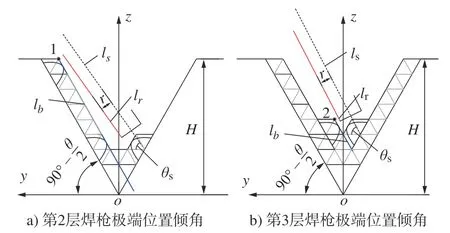
图8 焊枪碰壁模型示意图Fig.8 Model of the welding gun hitting the wall
此时坡壁的倾角为90° -θ/2:设在进行第2层焊接时,焊炬倾角为θs,焊炬半径为r,则焊炬中心线ls的方程为
此时直线lr的方程为
当处于第2层焊道时,直线lr与lb的极限交点为图中的黑点1 , 该点在yoz平面的坐标为从而可进一步求出此时直线lr的倾角为。为了避免碰撞,需要焊枪在第2焊层时左边的焊枪倾角θ1>,则右边的倾角为180°-θ1。
当焊层在第3层及以上时,由于空间偏置轨迹的对称性且空间较为狭小,在底部焊道完成后进行轮廓偏置轨迹时,需保证焊枪不碰触到沿z轴对称的焊道。此时直线的方程为
4 仿真分析
4.1 仿真结构模型的构建
为了验证上述理论的正确性,选用待焊工件的尺寸长200 mm、宽150 mm、厚40 mm 的低碳钢板,V 形坡口角度为60°,如图9 所示。
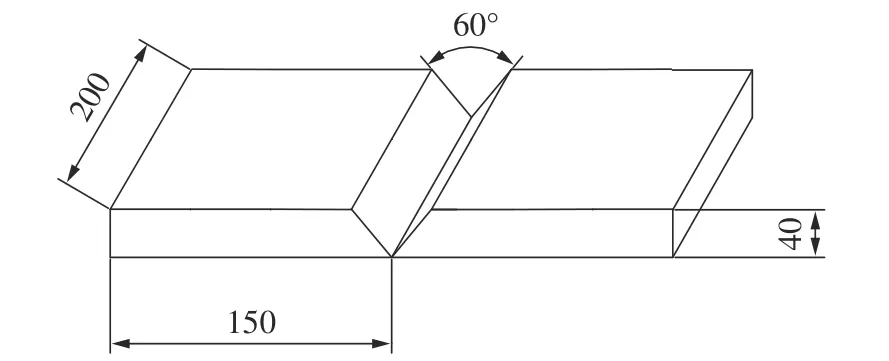
图9 待焊钢板尺寸Fig.9 Dimensions of steel plates to be welded
首先用Solidworks 对工件以及焊层进行三维建模,然后通过Hypermesh 软件进行网格划分,并将其导入到Simufact welding 6.0 中进行仿真分析。其中母材、焊缝以及焊丝材料均采用Q345 钢,对应牌号为S355J2G3。
4.2 热源模型和焊接参数的选择
焊道热源参数如表1 所示。对于填充焊道,为了便于比较,空间平行往复轨迹的焊接参数在空间轮廓偏置轨迹的基础上进行调整。令空间轮廓轨迹焊道尺寸的熔宽为6.48 mm、余高4.99 mm。则空间平行往复轨迹通过调整后的焊道尺寸为熔宽6.45 mm、余高4.99 mm,两者参数相差不大,可采用同一参数。实验过程中的焊接参数,均采用二次回归方程进行计算和选取。在仿真过程中,为了便于观察焊接完成后的变形量,只对其中一块钢板进行装夹固定,以便观察另外一块钢板的变形量。
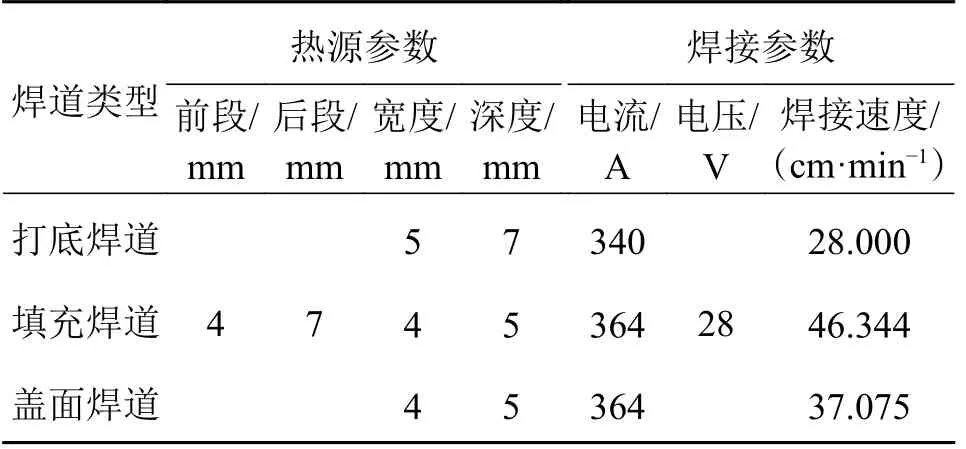
表1 热源模型参数及焊接参数的选择Tab.1 Selection of parameters for the heat source model and welding parameters
4.3 仿真结果分析
在保证焊接参数一致的条件下,通过对比空间平行往复轨迹、空间轮廓偏置轨迹、以及传统多层多道焊接方式之间的焊接变形量(分别标为方案1、方案2、方案3),由图10 所示的仿真结果可知,各方案的变形量如表2 所示。

表2 各方案焊接仿真变形量Tab.2 Deformation of welding simulation for each scheme
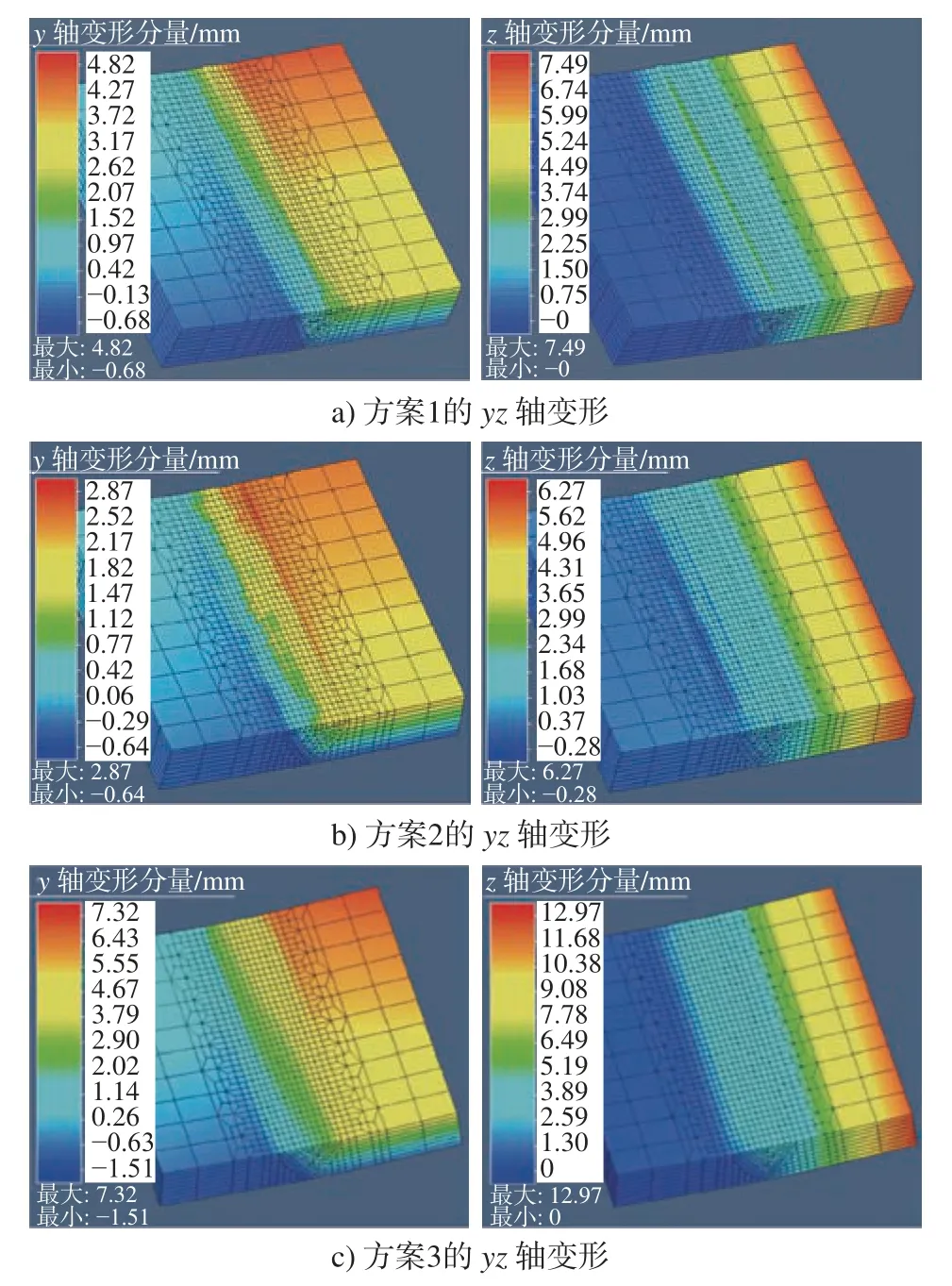
图10 仿真焊接变形量Fig.10 Simulation of welding deformation
由于焊接件结构的原因,x轴方向的变形量相对z、y轴而言可忽略不计[16],则从图10 和表2 可知,焊接后的变形量在y、z轴方向的降低都非常明显。与方案3 相比,方案1 在z轴上的变形量减少42.3%,在y轴方向的变形量减少了34.2%;方案2在z轴方向上的变形量减少了51.7%,在y轴方向的变形量减少了60.8%。
4.4 试验结果分析
为了进一步验证方法的可行性,焊接试验采用了FANUC M-20iA 工业机器人以及Phoenix 552 plus XR 焊机。焊接试验平台如图11 所示。

图11 焊接试验平台Fig.11 Platform for welding test
选用待焊工件的尺寸为100 mm×100 mm×20 mm 的Q345 钢板,V 形坡口角度为60°,并对距离坡口底端50 mm 处做好标记。所采用的焊丝为Ø1.2 mm ER50-6,保护气体为80%Ar + 20%CO2,气体流量为15 L/min。焊接参数如表3 所示。
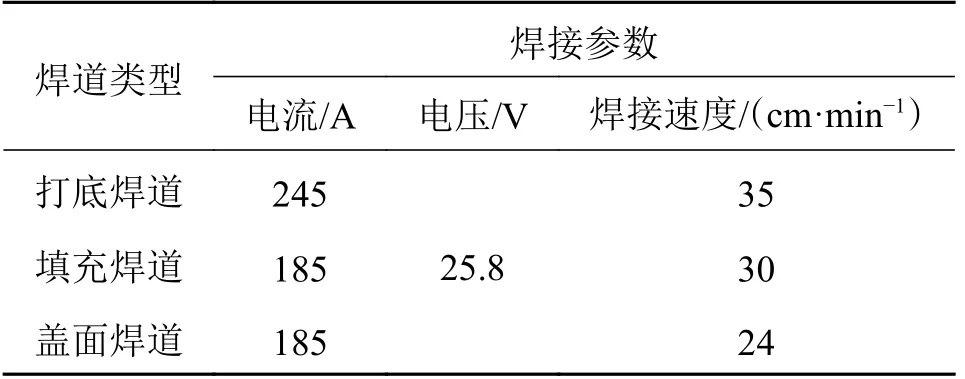
表3 试验焊接参数Tab.3 Parameters for test welding
焊接试验结果如图12 和表4 所示,与方案3 相比,方案1 在z轴上的变形量减少了37.3%,在y轴方向的变形量减少了5%;方案2 在z轴方向上的变形量减少了49.3%,在y轴方向的变形量减少了47.5%。可见方案1 在实际情况中,在y轴方向上的变形相对较大。

表4 各方案焊接试验变形量Tab.4 Deformation for each welding test scheme

图12 试验焊接变形量Fig.12 Deformation of Test Welding
该试验结果一方面验证了前述通过V 形焊层堆积方式可以减少工件焊接变形的理论论述。另一方面,方案1 与方案2 在z轴方向上的变形量相比,方案2 的变形量比方案1 少29.4%;在y轴方向上,方案2 的变形量要比方案1 少44.7%;进一步证明方案1 的焊接热量在V 形坡口的前端更容易集中堆积,不便于散发,从而导致坡口发生较为明显的横向变形。所以方案2 相对于方案1 来说,不仅在空间上更具对称性,而且在坡口较宽处的散热特性更好,更有利于降低前后端的焊接变形,但从编程和操作效率上来说,方案1 相对方案2 简单且直观。
因此,在实际焊接过程中,考虑到方案1 焊枪位姿的可调性,故可以根据V 形坡口的尺寸特性,综合考虑焊接变形量和焊接效率,可交替使用空间平行往复轨迹和空间轮廓偏置轨迹。前期坡口较窄,可采用空间平行往复轨迹,后期坡口较宽,为了减少前端大量热量堆积可采用空间轮廓偏置轨迹。
5 结论
本文主要介绍了一种面向中厚板V 形坡口的新型多层多道焊接方法,并对该方法从理论上进行了深入阐述,建立了两种方法的轨迹解析方程和焊枪倾角偏置方程;同时应用仿真软件将两种方法与传统焊接方法进行了对比分析,得出了以下结论:
1)根据坡口形状,采用V 形焊层的焊接方式相对于传统的逐层堆积方式,散热效果更好,在y、z轴方向的变形量均有显著降低。
2)通过在y、z轴方向变形量的仿真分析与试验计算,得出空间轮廓偏置轨迹优于空间平行往复轨迹的结论。
3)空间平行往复轨迹在轨道变换过程中焊枪的空间位姿调整相对简单、引入误差少、控制精度高,更适合具有坡口较窄、长度较短等特征的V 形坡口;而空间轮廓偏置轨迹更加适用于坡口较宽,长度较长的情况。

