卧式套管潜热蓄热单元偏心与肋片结构优化模拟

张璐荻，周国兵

（华北电力大学能源动力与机械工程学院，北京 102206）

我国能源行业在国家“双碳”目标指引下大力加强可再生能源利用[1]。以太阳能为代表的可再生能源具有安全清洁、总量大和分布广等诸多优点，但同时也存在分散性、间歇性和不稳定性等诸多问题，使得能源利用的供需侧存在时间、空间上不匹配的矛盾，这些问题凸显了发展热能储存技术的必要性。热能的储存可分为显热、潜热和化学热储存三种形式。其中，潜热蓄能，又称为相变蓄能，主要是利用相变材料(phase change material，PCM)在物态变化时所释放或吸收的大量潜热，具有蓄热密度高(为显热蓄能的5～10 倍[2])、蓄/释热温度稳定、易控制等优势[3]，但除金属/合金类PCM 外，大多数PCM 的热导率均较低，难以满足工业应用中对蓄放热速率的需求，已成为制约相变蓄能系统广泛应用的主要瓶颈之一。因此，强化传热技术一直以来都是相变蓄能领域的研究重点之一，目前着眼于PCM 本身和相变蓄能系统两个方面，包括提高系统传热系数、增大传热温差、扩展接触面积等。提高蓄热材料导热系数目前主要是通过添加各种填料来实现的，包括金属或氧化物纳米颗粒[4-5]、纳米碳材料(石墨烯、碳纳米管等)[6]、泡沫金属和膨胀石墨等多孔介质[7]。增大换热流体(heat transfer fluid，HTF)与PCM 间的换热温差可以显著提高PCM 的蓄放热效率，还可以利用梯级相变技术，即将具有不同相变温度的PCM 按照一定的顺序排列布置形成具有一定相变温度梯度的复合相变蓄热系统[8]。扩大PCM和换热器结构之间的接触面积也是增强传热的一种非常有效的方法，包括PCM 封装[9]、添加肋片等。由于成本低且易于制造，肋片常用于扩展工业设备中的换热面积，学者们通过实验和数值研究，分析了各种肋片参数对潜热蓄能系统的影响，如肋片的形状、分布、材料和厚度[10-13]。

除了上述方法，增强PCM内部的自然对流是提高相变蓄热系统性能的新思路。通过水平壳管式相变蓄热系统的结构变化来提高内部自然对流强度的一个简单措施是调整内管相对于外管中心的相对位置，即偏心布置。Yusuf等[14]通过实验研究了偏心布置对卧式壳管潜热蓄热装置传热性能的影响。通过在重力方向上移动内管到三个不同位置来改变偏心率，发现与同心布置相比向下偏心距离为30 mm时，完全熔化时间减少了67%。Yazici 等[15]在保持入口温度和质量流量不变的情况下研究了偏心布置对石蜡凝固的影响，发现随着偏心率增加，总凝固时间增加。然而对于不同参数不同系统设备尺寸，获得合适的偏心距离颇具挑战性。Zheng等[16]指出在某些条件下获得的偏心距可能不适用于其他情况。

本工作通过对卧式套管潜热蓄热单元的流场与温度场分析提出了“偏心面积比”这一新参数评价偏心布置蓄热单元的性能，并通过数值模拟对较佳偏心位置进行预测，此外针对偏心结合肋片的强化传热问题，在预测的较佳偏心位置对不同形式的肋片进行了数值模拟以分析其性能，为相变蓄热单元强化传热设计提供参考。

1 物理及数值模型

1.1 物理模型

卧式套管相变蓄热单元的物理模型如图1所示。该装置由外管和内管组成，长度l均为500 mm。外管内径D为40 mm，外设保温层；内管内径d为10 mm，管材为铜，管壁厚度δ为1 mm。蓄热单元的基本结构是同心的，y用于描述内管中心相较于基本结构的偏心距离。选择水作为HTF从内管流过，硬脂酸(stearic acid，SA)为PCM 填充在内管与外管之间的环形空间，表1 为SA、水和铜的各项热物性参数。

表1 硬脂酸、水和铜的热物性参数[2]Table 1 Thermophysical properties of stearic acid,water, and copper[2]

图1 卧式双管相变蓄热单元物理模型Fig.1 Schematic diagram of horizontal double-tube latent heat storage unit

1.2 数学模型

相变传热问题具有很强的非线性，传热过程同时存在导热、自然对流和固液相变。为简化计算，假设如下：①相变材料在蓄热单元中均匀且各向同性；②PCM 的密度采用Boussinesq 假设，即密度仅在浮升力项中随温度变化；③不考虑黏性耗散产生的热量；④液态PCM 为不可压缩牛顿流体；⑤蓄热单元初始温度分布均匀，忽略蓄热单元散热损失；⑥模型中流动为非稳态不可压缩流动，采用层流模型。

基于以上假设，建立潜热蓄热单元传热过程数学模型。采用焓-孔隙率法对PCM熔化和凝固进行求解，其中两相混合区(糊相区)视为多孔介质。当PCM熔化时，多孔介质的孔隙率从0增加到1；当PCM 凝固时，孔隙率从1 降低到0。控制方程如下[13,17]：

连续性方程：

式中，t为时间，s；ρ为密度，kg/m3；p为压强，Pa；μ为动力黏度，kg/(m/s)；β为热膨胀系数，K-1；g为重力加速度，m/s2；T为温度，K；Tref为参考温度，根据Boussinesq 假设，该值假定为PCM的固相线温度，K；源项S为达西定律阻尼项：

式中，Amush为糊相区常数并取值105用于计算[17]，b是小于0.0001 的常数，以免分母为零，f为液相率，表示为：

式中，hlat为潜热焓，kJ/kg；L为熔化潜热，kJ/kg；TS和TL分别为PCM的固相线温度和液相线温度，K。

能量方程：

式中，k为导热系数，W/(m/K)；Cp为比热容，kJ/(kg·K)；PCM 总焓htot包括显热焓hsens和潜热焓h

lat：

式中，Tref是参考温度，K；href为参考温度下的焓值，kJ/kg；L为熔化潜热，kJ/kg。

㶲效率也用于分析蓄热单元的性能，其定义为PCM中储存的㶲与HTF提供的㶲之比：

式中，ψ为潜热蓄热单元的㶲效率，Exsto和Exinp分别为PCM 中储存的㶲和HTF 提供给蓄能单元的㶲，kJ。ṁHTF为HTF的质量流量，kg/s；THTF,in和THTF,out分别为潜热蓄热系统入口和出口处的HTF温度，K；T0为环境温度即系统的初始温度，K；TPCM为PCM的平均温度，K。

1.3 边界条件和数值求解

由于所研究卧式相变蓄热单元的几何结构是轴对称的，为了节省计算资源，取原始结构的1/2 为计算域，选用多面体网格进行划分，网格质量保证在0.7以上，如图2所示。

图2 计算域网格划分Fig.2 Mesh generated in computational domain

初始时刻PCM的温度分布均匀，为40 ℃：

HTF入口采用速度入口边界条件，相应的入口速度(Re=2000)，温度为：

在HTF 出口处，采用outflow 出口边界条件，认为出口处流动充分发展：

内管的内、外壁面应用耦合边界条件，外管壁面根据假设为绝热边界条件：

采用基于有限体积法的ANSYS Fluent 软件对模型进行数值求解。SIMPLE算法用于求解压力-速度耦合，PRESTO!方法离散压力项。能量和动量方程采用二阶迎风格式离散。压力、速度、液相率和能量的亚松弛因子分别设置为0.3、0.7、0.9 和1。连续性、动量和能量方程的残差收敛标准分别设置为10-5、10-5和10-6，每个时间步长的最大迭代次数设置为20。

1.4 无关性验证和模型验证

为了验证网格和时间步长的独立性，计算了同心布置中不同网格数和时间步长的PCM 液体分数变化，如图3 所示。图3(a)表明1.6×105和1.9×105的网格数之间的液相率最大偏差为9.3%，而1.9×105和2.4×105之间的偏差为1.8%。图3(b)中，液相率在0.5 s和0.1 s的时间步长之间的最大偏差为13.6%，而在0.1 s 和0.05 s 之间的偏差为3.4%。因此，选取时间步长0.1 s和1.9×105规格的网格来确保计算的准确性。

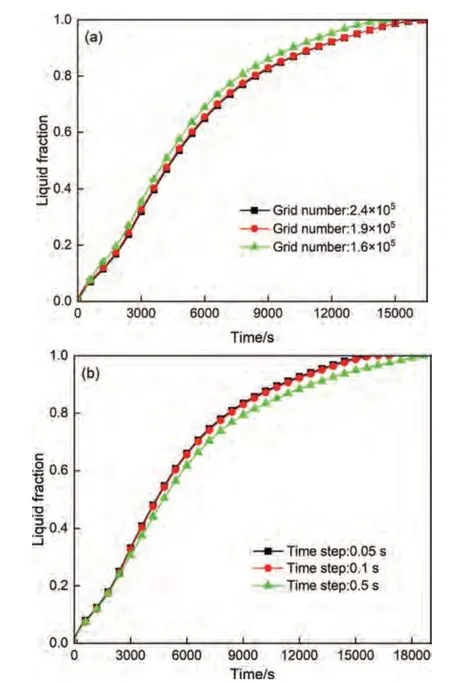
图3 (a)网格无关性验证；(b)时间步长无关性验证Fig.3 (a) Grid number independence verification;(b) Time step independence verification

为了验证当前模型和求解方法的正确性，将上述模型与Hosseini 等[18]的实验结果进行对比，如图4 所示。可见当前模型与Hosseini 等[18]结果之间PCM 平均温度最大偏差小于1.4%，表明计算模型是可靠的。

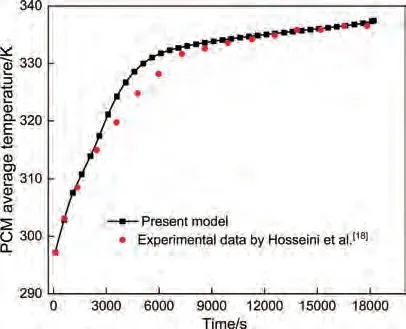
图4 本文模拟与Hosseini等[18]的实验结果比较Fig.4 Comparison between the present model predictions and experimental results of Hosseini et al.[18]

2 结果与讨论

2.1 熔化过程分析和偏心面积比

图5为卧式套管相变蓄热单元在长度方向上的中间截面处(z=l/2)的温度、液相率和流线随时间变化的分布。在每个截面中，左半部分为熔化过程温度分布，右半部分为带有流线的液相率分布。

图5 蓄热单元中间界面处(z=l/2)随时间变化的温度云图(左)和带流线分布的液相率云图(右)Fig.5 Temperature contours (left half) and liquid fraction contours with streamlines (right half) at z = l/2 during the melting of PCM for concentric position

可以看出，在熔化的初期2000 s 左右时液相份额还很少，主要围绕内管壁面呈环形分布，此阶段液相内部温度分布比较均匀，无法产生足够的密度差，因此在这一时期，自然对流效果很弱，导热在蓄热单元的传热机理中占据主导地位。

随着熔化过程的进行，蓄热单元内部PCM 的液相在单元上部积聚，这主要是因为内部液相温度分布不均匀引起的密度差导致了强烈的自然对流起到了强化传热的作用，使得蓄热单元上部的熔化过程加快。从流线上也可以看出该阶段单元上部流动更加剧烈，这时蓄热单元的传热机理为自然对流主导。

随着自然对流的持续强化传热作用，当熔化时间为8000 s时蓄热单元的上部区域已经完全熔化，从温度云图可以看出此时单元上部液相温度分布比较均匀，而在单元下部区域PCM 处于较低温度，这种向上的温度梯度使得自然对流效果减弱且很难影响到单元下部区域。因此单元底部依靠导热需要更长的时间去完全熔化(16000 s)，此时的传热机理又变为导热主导，并且由于相变材料热导率低的原因使得下部区域成为更难熔化的区域。

因此基于上述分析可以将蓄热单元内部根据传热机理不同划分为两个区域，如图6所示，即自然对流主导区域(温度云图中红色部分)，弱自然对流与导热主导区域(温度云图中分层温度部分和蓝色部分)。

采用偏心布置可以扩大熔化较快的自然对流主导区域，缩小熔化较慢的弱自然对流与导热主导区域面积，进而缩短蓄热单元整体熔化时间，所以两个区域的面积关系是决定卧式套管偏心相变蓄热单元的固有因素。在此基础上提出了一个新的参数“偏心面积比”来评估偏心蓄热单元的性能，其定义如下：单元截面图上自然对流主导区域面积(A1)和弱自然对流与导热主导区域面积(A2)之比，即：

为获得设计蓄热单元的较佳偏心面积比利用数值模拟展开研究。

2.2 蓄热单元的偏心优化

为了获得偏心面积比和完全熔化时间的关系，模拟了在不同偏心面积比的熔化过程(Tin=85 ℃，入口Re=2000，win=0.073 m/s)，表2 列出了5 个不同偏心面积比(同心布置和ɛ=4∶1、8∶1、16∶1、24∶1)的偏心距离y。

2.2.1 液相率与熔化云图

图7 表示不同偏心面积比的液相率随时间变化，可以看出不同偏心面积比下的液相率上升呈类似趋势，与2.1节分析获得的熔化过程一致。另外，还发现完全熔化时间随着ɛ的增加而不断减少，当达到16∶1时获得最短的熔化时间8700 s，相较于同心布置缩短了45.8%。然而当偏心面积比增加到24∶1时，总熔化时间反而会增大到9070 s，这主要是因为偏心过大，下部区域的导热主导面积变得非常小，以至于在熔化初期几乎完全熔化，比上部要早得多，导致上部区域的熔化负荷比下部区域的更大，从而整个单元的总熔化时间变得更长。

图8为不同偏心面积比熔化过程的温度与液相率云图，可以看出对于各偏心面积比情形，在熔化初期内部的熔化前沿在导热作用下具有相同趋势，并且随着熔化过程进行，在较小偏心面积比情况下，上部自然对流主导域的熔化前沿均比下部导热区域先到达蓄热单元边界。在较佳偏心ɛ=16∶1处则是上部区域和下部区域的熔化前沿同时到达蓄热单元边界。当偏心面积比继续增加时，可以看到下部区域的熔化前沿在初期就已经到达了单元下边界，而上部区域还在向外扩展，这也解释了为什么偏心过大反而会增加熔化时间。理论上，当自然对流主导区域的熔化前沿和导热区域的熔化前沿同时分别到达蓄热单元的上、下边界时即可获得此时的最佳偏心，这也对偏心面积比这一参数的合理性给予了证明。但获得的较佳偏心面积比在16∶1附近是只针对当前使用的材料(SA)获得，对于其他材料，可以预期最佳偏心面积比与使用材料的自然对流强度和导热能力之间的比值有直接相关。

图8 不同偏心面积比的温度(左)和液相率(右)云图(z=l/2)Fig.8 Temperature (left half) and liquid fraction contours (right half) with varying eccentric area ratios

2.2.2 㶲效率分析

图9为不同偏心布置下㶲效率随时间变化曲线图，可以发现蓄热单元的㶲效率都呈现出随时间增加的趋势，这是因为随时间推移，PCM 温度逐渐升高与HTF 之间的温差减小，进而㶲损失逐渐减少，系统的㶲效率逐渐增加。还可以看到随偏心面积比的增加㶲效率呈下降趋势，这主要是因为随偏心面积比增大，单元上部自然对流主导区域面积增加，避免了由于对流强烈而产生的过热现象，内部温度更加均匀，所以在熔化过程大部分时间里大偏心面积比的平均温度相对更低，与HTF的温差相对更大，导致了㶲损失更大，㶲效率变低。但由于偏心布置会加快熔化速率，所以在后期大偏心比由于已经全部熔化，单元整体温度高于相变温度，平均温度更高，温差变小，相较于小偏心布置㶲损失更少，所以在图9看出在熔化后期不同偏心㶲效率之间差距缩小，这意味着偏心布置虽然缩短了蓄热单元的熔化时间，但会使蓄热单元㶲效率略有降低。

图9 不同偏心面积比的㶲效率--时间曲线Fig.9 Time dependent exergy efficiency with varying eccentric area ratios

2.3 偏心布置与肋片结合

上述分析得到的较佳偏心面积比16∶1相较于同心布置完全熔化时间缩短了45.8%，但从图8液相率云图中可以看出在蓄热单元靠近左右边界处熔化还是较为缓慢，因此尝试利用扩展接触面积与偏心布置相结合的方式来进一步加速内部熔化过程。本工作在ɛ=16∶1的基础上设计了三种不同的肋片结构，分别为螺旋肋、十字肋和X形肋，其结构和尺寸如图10 所示，为便于比较，这三种不同形状的肋片具有相同的体积，沿肋片伸展方向上厚度均为1 mm。

图10 三种肋片结构及尺寸Fig.10 Structures and sizes of three kinds of fins

图11 和图12 分别为三种肋片结构的液相率随时间变化曲线图和熔化过程长度方向中间截面处的温度和液相率云图。从图11 可以看出有螺旋肋、十字肋和X形肋的偏心蓄热单元结构的完全熔化时间分别为6910 s、5930 s 和5510 s，相较于偏心面积比同为16∶1的无肋片基础结构熔化时间分别缩短了20.6%、31.8%和36.7%。其中螺旋肋片对熔化速率的提升效果较差，这主要是因为螺旋肋相较于其他两个肋扩展的换热面积更小，所以初期导热主导阶段液相率上升相对缓慢，从图12 云图上也可以看出在自然对流主导的阶段其影响并未达到单元左右边界以加速其熔化。而十字肋和X形肋由于拥有相同的扩展换热面积，所以在熔化初期导热主导阶段液相率上升具有相近速率，而从云图上可以看出十字形肋片的上、下肋分别加速了熔化前沿在单元上、下方向的扩展速率，左右肋片也因增加横向的扩展面积而扩大了上部自然对流的影响范围，并且可以看出也对较难熔化的单元左右边界起到一定强化作用。相比之下，X形肋片同时具有增强导热和自然对流的作用，既利用肋片的结构直接导热作用扩大传热面积加速了单元左右边界熔化，又因其肋片有一定倾斜角度引导自然对流沿其流动，进而其影响范围也扩大到了单元左右边界，所以具有更好的强化传热效果。

图11 不同结构肋片与无肋单元的液相率--时间曲线Fig.11 Time dependent liquid fraction with varying fin structures (ε=16∶1)

图12 不同肋片结构的温度(左)与液相率(右)云图(z=l/2)Fig.12 Temperature (left half) and liquid fraction contours (right half) with varying fin structures

3 结 论

本工作建立了卧式套管相变蓄热单元数学模型，并对环形空间内PCM 的熔化过程进行数值模拟，以获得潜热蓄热单元强化传热的较佳偏心与肋片结构。相关结论如下。

（1）通过对卧式套管相变蓄热单元熔化过程流场与液相扩展分析，将熔化过程划分为三个阶段：导热主导的初始阶段，随后是自然对流和导热的混合作用中间阶段，以及导热再次占主导的最终阶段。并据此将PCM 分布的环形空间划分为两个区域，进而提出新的评价参数“偏心面积比”。得出硬脂酸为PCM 时较佳的偏心面积比位于16∶1 附近，熔化时间相对于同心布置缩短了45.8%。

（2）针对偏心潜热蓄热单元进行了㶲效率分析，发现蓄热单元的㶲效率呈现出随时间增加的趋势，并且随着偏心面积比的增加㶲效率呈下降趋势，即偏心布置缩短了蓄热单元的熔化时间，但会使单元的㶲效率略微降低。

（3）利用偏心布置结合肋片的方法进一步强化传热，设计了螺旋肋、十字肋和X 形肋三种结构，在同为ɛ=16∶1条件下，相较于无肋结构熔化时间分别缩短了20.6%、31.8% 和36.7%，采用偏心结合X形肋的结构可以获得较佳性能。

符号说明

Amush—— 糊相区常数

A—— 面积，mm2

Cp—— 比热容，kJ/(kg·K)

D—— 外观内径，mm

d—— 内管内径，mm

EX—— 㶲，mm

f—— 液相率

g—— 重力加速度，m/s2

h—— 比焓，kJ/kg

k—— 导热系数，W/(m·K)

L—— 潜热，kJ/kg

l—— 长度，mm

m—— 质量流量，kg/s

p—— 压力，Pa

Re—— 雷诺数，量纲为1

S→—— 源项

T—— 温度，K

t—— 时间，s

u,v,w——X,Y,Z方向速度，m/s

y—— 偏心距离，mm

希腊字母

ρ—— 密度，kg/m3

μ—— 动力黏度，kg/(m·s)

β—— 热膨胀系数，K-1

ψ—— 㶲效率

δ—— 厚度，mm

ɛ—— 偏心面积比

下标

S—— 固态

L—— 液态

PCM—— 相变材料

HTF—— 换热流体

sens—— 显热

lat—— 潜热

tot—— 总热

ref—— 参考

sto—— 储存

inp—— 输入

in—— 入口

out—— 出口