多尺度分解下GRU-TCN集成的动力电池剩余使用寿命预测方法

刘 佳，马志强,3，刘广忱，高俊东，李宏勋

（1内蒙古工业大学数据科学与应用学院；2内蒙古工业大学大学电力学院；3大规模储能技术教育部工程研究中心，内蒙古 呼和浩特 010080）

作为新能源汽车的关键部件，动力电池的循环寿命、技术水平和安全性直接决定了新能源汽车的续航效果、性能和安全性。随着新能源汽车市场的不断扩大，动力电池的需求量也在不断上升。锂电池作为目前主流的动力电池之一，存在安全性差、成本高、循环寿命短等缺点。精准预测动力电池的RUL，能够提前规避因电池过度使用带来的风险，在电池故障前发出警告，还能在退役电池的二次利用中为使用者提供决策依据，在安全可行的范围内提升电池第二寿命的利用率，既能提升动力电池的安全性，还能在一定程度上降低使用成本，实现资源的循环利用。一般认为，当电池容量衰退到原始容量的70%时达到失效阈值，电池的RUL 代表当前状态下电池容量衰退到失效阈值前的剩余循环次数。

现有的方法中，电池的RUL 预测主要分为基于模型的方法和数据驱动的方法[1]。基于模型的方法旨在建立一个描述电池退化行为的数学模型来预测未来的电池性能变化。Sadabadi等人[2]使用电化学模型提取电池容量衰退的相关特征，实现了不同操作条件下的电池RUL 预测，但该方法建模计算复杂度高且需要大量的专业知识作为支撑。Wang等人[3]使用粒子滤波(particle filtering，PF)和卡尔曼滤波(Kalman filtering，KF)算法表征电池的容量退化并预测电池的RUL，PF 在一定程度上解决了KF 只适用于线性高斯系统的问题，但同时又带来粒子退化的问题。在1C 电流下，内阻与电容线性相关，基于这一关系，Guha 等人[4]提出了基于PF的内阻增长模型以更加准确地预测电池的RUL，但该方法只考虑了相同放电速率的情况，没有考虑不同放电速率和温度变化等其他因素的影响。Zhang等人[5]采用线性优化组合重采样的方法以提高RUL预测精度，但依旧面临着粒子退化和粒子多样性缺陷问题。

基于数据驱动的方法只需要历史数据而不需要充分了解电池内部机理及循环过程，相较于基于模型的方法来说更加灵活。王萍等人[6]基于高斯过程回归(Gaussian process regression，GPR)和最小二乘支持向量机(least squares support vector machine，LS-SVM)实现了SOH和RUL联合预测，但该方法对异常值较为敏感，电池容量回升现象及异常值均会对预测结果产生较大影响。廖力等人[7]通过对动力电池的多个健康因子进行相关性分析，提出了一种多健康特征融合及IGSA-SVR 的SOH和RUL 联合预测方法，但该模型的网络结构相对简单，可能无法准确捕捉到一些复杂的非线性关系。随着深度学习的发展，吴忠强等人[8]使用PFLSTM模型实现了电池的RUL预测，相较于其他模型，神经网络模型通常具有更灵活的网络结构和自适应学习的能力，能够更好地处理复杂的非线性关系，但该方法忽略了LSTM 的长期依赖性问题。Chen 等人[9]为了减小电池容量再生期间的噪声影响，使用去噪自编码器(denoising auto-encoder，DAE)来处理电池原始数据，并使用Transformer捕获时间信息和特征，在RUL 预测任务上取得了较好的效果，但DAE 在非线性噪声和混合噪声的处理上有一定的局限性，并没有显著地提升预测精度。Hong 等人[10]开发了第一个用于快速预测锂离子电池剩余使用寿命的端到端的深度学习框架，通过考虑时序特征及多HIs的相关性，来寻找电池退化期间更显著的特征，实现了更快、更准确的电池RUL预测，但该方法没有考虑多HIs之间的耦合关系，同时引入多HIs进行预测时可能会引入冗余特征，导致模型精度下降。董渊昌等人[11]使用奇异值分解(singular value decomposition，SVD)对锂电池容量的多个HI 进行了特征提取，再通过Spearman 相关性分析，挑选出与原始锂电池容量数据相关性极高的7 个HI 通过堆叠自编码器(stacked autoencoder，SAE)进行特征融合，最后使用GPR对该融合HI进行预测，有效提升了RUL预测的精度，该方法仅仅考虑了各HI 与电池容量数据的相关性，仍然忽略了多HIs 之间的耦合关系。由于锂电池的容量衰退过程中所体现出的各种非线性特征以及容量回升现象，Liu 等人[12]通过经验模态分解(empirical mode decomposition，EMD)方法，将原始电池容量数据自适应分解为一些固有模态函数(IMFs)和残差，然后利用长短期记忆网络(long short-term memory，LSTM)和GPR分别对IMFs 和残差进行预测，因此捕获到了容量的长期依赖性和容量再生现象的不确定性波动，但EMD 方法容易产生模态混淆的问题，即分解出的单个IMF可能同时包含了低频和高频的数据，不能有效地根据时间特征对不同频段的数据进行有效分解。

综合以上分析，为了降低动力电池RUL预测任务中噪声和容量回升现象导致的非线性特征对RUL预测精度的影响，本工作提出了一种基于EEMD多尺度分解下门控循环单元网络与时序卷积网络集成的动力电池RUL预测方法，首先使用EEMD对原始数据进行分解，将噪声和容量回升现象导致的非线性特征及原始容量数据的主要趋势分解到对应的高频分量和低频分量，再使用GRU和TCN网络分别对高频分量和低频分量进行预测，最后使用Attention对预测结果进行集成。在NASA数据集上进行了对比实验、不同预测起点实验及消融实验，实验结果表明该集成模型能够有效降低动力电池RUL预测任务中噪声和容量回升现象导致的非线性特征对RUL预测精度的影响，相较于典型单一模型和其他同类型模型具有更高的准确性和稳定性。

1 方 法

1.1 RUL定义

电池老化分为存储老化和循环老化。存储老化被定义为电池在空闲或存储条件下，由于两个电极的自放电引起的容量衰减的不可逆变化，电池容量衰减到失效阈值所经过的时间，称为搁置寿命或贮存寿命。循环老化被定义为电池充放电过程中，使用模式、温度条件和电流作用引起的容量衰减变化，电池容量衰减到失效阈值之前能反复充放电的次数称为循环寿命。为了更加清晰地定义动力电池的RUL，首先引入动力电池的健康状态(state of health，SOH)定义。

动力电池的SOH 用于描述电池长期的健康状态，通常由随电池老化而改变的电池参数表征，主流方法是使用容量定义动力电池的SOH。计算公式(1)如下。

其中，C(0) 表示动力电池的初始容量，Cmax(n)表示动力电池在循环n时的最大容量。随着电池循环次数的增加，电池的SOH 值呈下降趋势，表明电池性能退化，当电池满充状态的容量下降到标称容量的70%时，认为动力电池寿命终止。

动力电池的RUL 通常定义为在达到失效阈值之前剩余的循环次数，即动力电池的循环寿命。计算公式(2)如下。

其中，NRUL为电池的RUL，即电池在达到失效阈值之前剩余的充放电次数，NEOL为电池容量由初始状态退化到失效阈值时电池经历的循环次数(即SOH 下降到70%时动力电池的循环次数)，NECL为电池当前状态下已经历的循环次数。

1.2 动力电池RUL预测模型

为了分离原始信号中混淆的多个固有模态数据，获取相对平滑的模态特征，并最小化数据重构过程的噪声影响，从而降低噪声和容量回升现象导致的非线性特征对动力电池RUL预测精度的影响，本工作提出一种多尺度分解下GRU-TCN 集成的动力电池RUL预测模型，如图1所示。该模型主要包括三个模块：数据分解模块、时序预测模块、数据重构模块。

图1 动力电池RUL预测架构图Fig.1 Power battery RUL predictive architecture diagram

1.2.1 数据分解模块

为了减少分解过程中噪声对原始数据的影响，且考虑到原始数据的非线性特征，使用具有一定抗噪性、能够自适应分解非线性信号的EEMD[13-14]方法对原始信号进行分解。经过分解后，原始信号被分解为不同的固有模态函数，从而将包含原始信号主要部分的低频分量与包含高频噪声的高频分量分解，使各个分量具有相对平滑的特性，能够提高时序预测的准确性。在数据分解模块中，将电池原始容量序列X作为EEMD分解的输入，输出高频分量XH1、XH2、XH3及低频分量XL作为时序预测模块的输入。

1.2.2 时序预测模块

分别使用TCN[15]和GRU[16]预测低频分量和高频分量。低频分量包含了原始数据的长期变化趋势，因此选择具有更大感受野的TCN 对低频分量进行预测，相对于卷积神经网络[17](convolutional neural network，CNN),TCN引入了循环结构和残差链接，能够更好地处理原始数据的动态模式，并且具有更大的感受野，使得信息可以在网络中传播更长的时间跨度，从而更好地捕捉序列数据中的长期依赖关系。 相对循环神经网络[18](recurrent neural network，RNN)，TCN的梯度消失和梯度爆炸的问题较小。高频分量的数据波动性较大，因此选择能够捕捉短期波动的GRU 对高频分量进行预测，能够更好地捕捉数据中的瞬时变化和短期趋势，提高预测的准确性。相对于RNN，GRU 能够更有效地传递梯度，避免梯度消失或梯度爆炸的问题，而相对于LSTM，GRU具有较小的参数和计算量，在相同的训练时间内，GRU 通常能够达到相近或者更好的性能。在时序预测模块中，将低频分量XL作为TCN 模型的输入，输出其预测结果为YL，将高频分量XH1、XH2、XH3 作为GRU 模型的输入，输出其预测结果为YH1、YH2、YH3，时序预测模块的输出结果将作为数据重构模块的输入。

1.2.3 数据重构模块

目前主流的EEMD数据分量重构方法是将各分量预测结果直接叠加得到最终的预测结果。但是在该方法的重构过程中，各个不同频率的分量之间可能相互影响、互相干扰，导致重构结果与原始信号不完全匹配，并且直接叠加重构会进一步放大EEMD分解过程中引入的误差，影响最终的预测结果。因此，本工作使用注意力机制[19]对预测结果进行加权平均集成(weighted average)。在数据重构模块的权重推理过程即Attention 的训练过程中，使用[XH1,XH2,XH3,XL]作为输入，通过线性变换计算查询(Query)、键(Key)和值(Value)，由键、值相乘得出注意力分数，使用softmax 对其进行归一化并以最小化损失函数为目标不断优化线性变换的参数、更新注意力分数，最终推理出注意力权重矩阵W。在数据重构时，将时序预测模块的预测分量矩阵[YH1,YH2,YH3,YL]作为Attention 的输入，与注意力权重矩阵W相乘得到动力电池容量衰退状态预测序列Y，由此得出NEOL，再由RUL 计算公式NRUL=NEOL-NECL即可得出动力电池RUL预测结果。

2 实验结果与分析

2.1 数据集和评价指标

本实验采用NASA 锂电池数据集[20]，选用B0005、B0006、B0007 号电池的历史容量数据作为研究对象，每个电池各包括168次充放电循环的历史容量数据，B0005、B0006、B0007 号电池的历史容量衰退曲线如图2所示，图中箭头所指为噪声及容量回升现象导致的非线性特征。测试电池额定容量为2.0 Ah，以额定容量的70%看作锂电池的失效阈值，即1.4 Ah，由于在原始数据集中B0007号电池容量没有下降到1.4 Ah以下，为了便于验证，将B0007 号锂电池的失效阈值设置为71%，即1.42 Ah。在本实验中，时序预测模块和数据重构模块均使用前T个循环周期的数据进行模型训练，使用第T个循环周期之后的数据对模型进行验证。

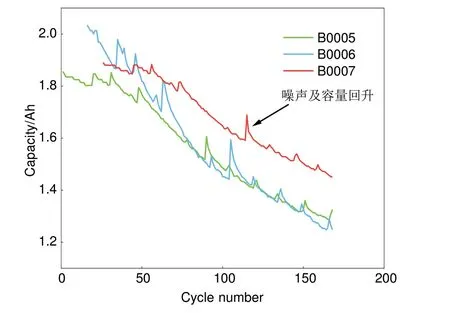
图2 NASA锂电池容量衰退曲线Fig.2 NASA lithium battery capacity decline curve

为了定量评估本模型的性能，本工作选取以下三个评价指标对模型进行评估。

（1） 平 均 绝 对 误 差(mean absolute error，MAE)，范围[0,+∞)，当预测值与真实值完全吻合时等于0，即完美模型；误差越大，该值越大。公式(3)如下所示：

（2）均方根误差(root mean square error，RMSE)，范围[0,+∞)，当预测值与真实值完全吻合时等于0，即完美模型；误差越大，该值越大。公式(4)如下所示：

（3）绝对误差(absolute error，AE)，范围[0,+∞)，当预测值与真实值完全吻合时等于0，即完美模型；误差越大，该值越大。公式(5)如下所示：

其中，i表示第i次放电循环，n表示预测放电循环总数，ŷi表示电池容量预测值，yi表示电池容量真实值，TRUL表示真实状态下动力电池的RUL值，T̂RUL表示预测的动力电池RUL值。

2.2 EEMD结果分析

以B0005 号电池为例，使用EEMD 对其原始容量衰退曲线进行分解，分解出4 个信号分量IMFs，按照各信号分量的频率由高到低排序，如图3 所示，IMF1 至IMF3 的信号频率较高，曲线波动性较大，视为高频分量，IMF4 曲线平缓，具有原始数据的主要趋势，视为低频分量。由分解结果做出以下假设：动力电池容量衰退过程中由噪声和容量回升现象导致的非线性特征被分解到高频分量，而原始容量数据的主要趋势被分解到低频分量，且低频分量中不再有噪声及容量回升现象导致的非线性特征，有利于提升动力电池容量衰退状态和RUL预测的准确性。此假设也在2.3节实验结果对比分析中得到了验证。

图3 B0005号电池容量衰退曲线分解结果Fig.3 B0005 battery capacity decline curve decomposition results

2.3 实验结果对比分析

为了测试提出的集成模型是否能够有效提升动力电池RUL 预测任务中动力电池容量衰退状态和RUL预测的精度，进行了一系列对比实验，在预测起点为80 的条件下，分别与3 种典型单一模型、4 种基于EEMD 的组合模型及1 种基于EEMD 的集成模型进行对比。本工作提出的集成模型是指在使用GRU和TCN分别预测EEMD分解所得的高频分量和低频分量的基础上，不采用当前主流的叠加重构的方法对数据进行重构，而是通过加权平均集成的方法对GRU 和TCN 模型的预测结果进行重构，使用Attention 对各分量的权重进行推理，并对GRU 和TCN 模型的预测结果进行加权求和。为了验证该集成方法对提升模型性能的有效性，实验在同等条件下对比了叠加重构和堆叠集成(Stacking)的数据重构方法。其中，叠加重构是指将时序预测模块的预测结果按列相加实现数据重构，不涉及模型训练及推理。堆叠集成采用GRU 对预测结果进行集成，其训练集是时序预测模块训练过程中各分量的预测结果及对应的原始数据，测试集是时序预测模块测试中各分量的预测结果及对应的原始数据。各模型对电池容量衰退状态的拟合情况如图4所示，各模型的评价指标值如表1所示。

表1 对比实验评价指标Table 1 Compare experimental evaluation indexes

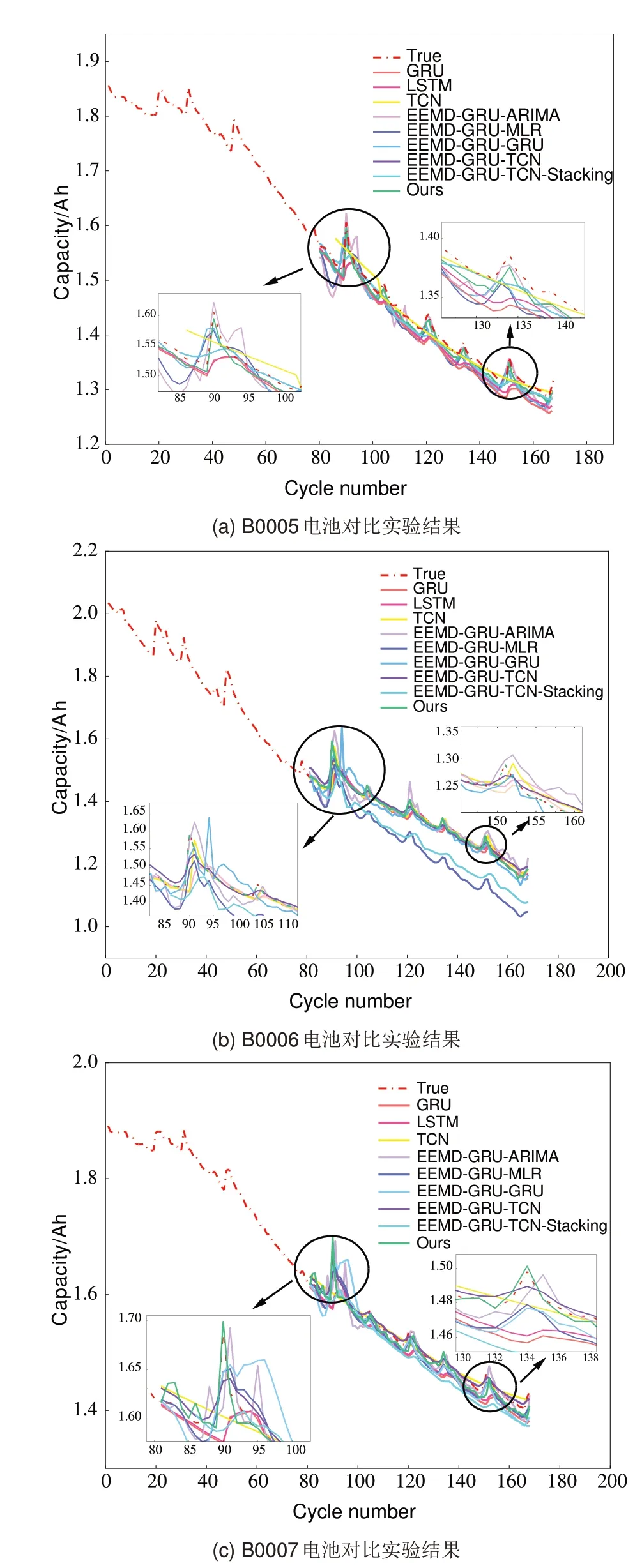
图4 对比实验结果Fig.4 Comparative experimental results

由图4 可得，在同等条件下，相较于单一模型，EEMD组合模型的预测曲线在噪声和容量回升部分更好地拟合了实际容量衰退曲线，这是由于EEMD方法能够分解原始容量数据中混淆的多个固有模态数据，由噪声和容量回升现象导致的非线性特征被分解到高频分量，原始容量数据的主要趋势被分解到低频分量，且低频分量中不再有噪声及容量回升现象导致的非线性特征，因此，此类基于多尺度分解的模型能够降低各模态之间的相互干扰，使得时序预测模型的输入数据相对平滑，提升模型预测精度。相较于其他同类型模型，本工作提出的集成模型对电池容量衰退的总体趋势及由噪声和容量回升现象导致的非线性特征的拟合具有更乐观的表现，这是由于EEMD方法对原始容量数据进行分解时引入了噪声，叠加重构会进一步放大噪声，而堆叠集成使用时序预测模块训练阶段的预测结果进行集成模型训练，也会引入噪声，本工作选择加权平均集成方法对预测结果进行数据重构，可以减少噪声的影响及不同频率分量之间的相互干扰。

由表1中数据可知，首先，用于对比的典型单一模型和其他同类型模型中最大MAE 和RMSE 分别为0.0128、0.0113 和0.0222、0.0178，本工作提出的集成模型最大MAE 和RMSE 分别为0.0052和0.0074。同等条件下，本工作提出的集成模型的MAE 和RMSE 均为最低值，这是由于分解后的分量相对平滑，使用GRU和TCN分别对高频分量和低频分量进行预测，能够很好地预测各个分量的特征变化。其次，本工作提出的集成模型的AE 值最低，平均不超过一个循环周期，且在不同电池数据下本工作提出的集成模型AE 值波动最小，而同样的分解和预测条件下，使用叠加重构的EEMDGRU-TCN 模型最大AE 值和最小AE 值分别为9 和0，使用堆叠集成进行数据重构的EEMD-GRUTCN-Stacking 模型最大AE 值和最小AE 值分别为15和7，这是由于使用Attention对预测结果进行加权求和，能够重点关注对电池容量衰退状态影响较大的分量，充分学习各分量与电池容量衰退状态之间的关系，避免了对分解噪声的二次放大和各分量之间的相互干扰，因此提升了动力电池RUL 预测的精度和稳定性。综合以上分析，本工作提出的集成模型能够提升电池容量衰退状态及RUL 的预测精度，并且相较于典型单一模型和其他同类型模型在动力电池RUL预测中具有更强的稳定性。

为了进一步测试工作文提出的集成模型的预测性能，将预测起点分别设置为70、80、90 和100进行RUL预测，其实验结果评价指标如表2所示。

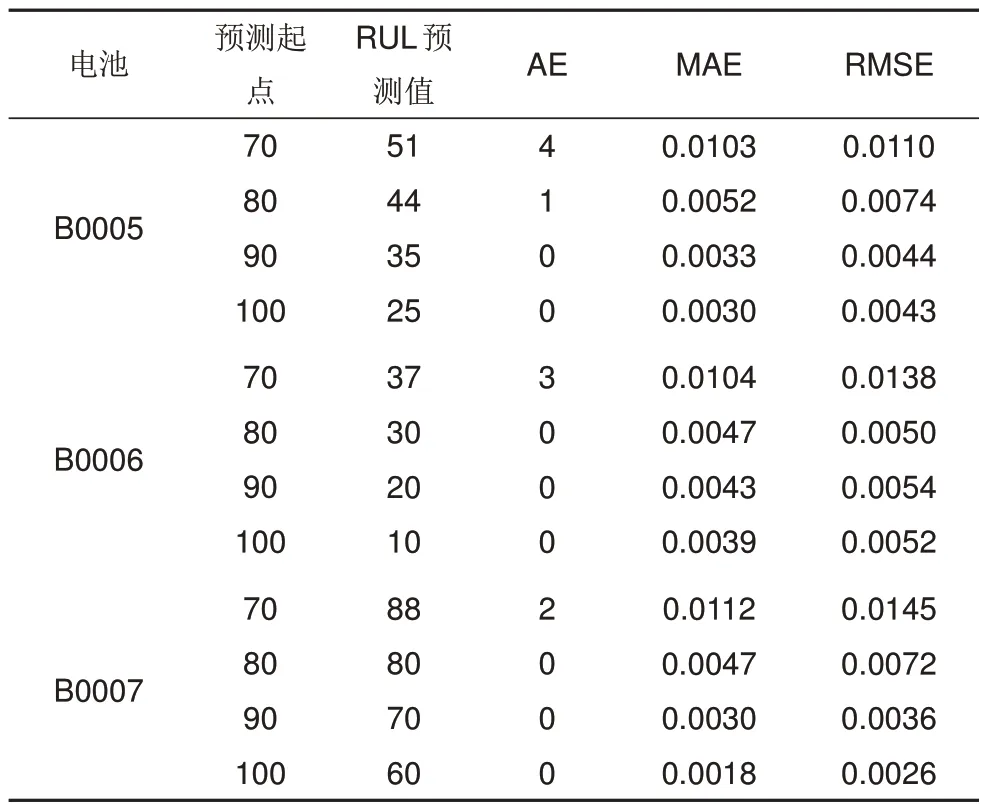
表2 不同起点对比实验结果Table 2 The experimental results were compared with different starting points

由表2可得，当预测起点为80、90、100时都能得到较为准确的RUL结果。当预测起点为70时，由于仅有70 条训练数据，模型未能充分学习和训练，AE 值相对较高，最高为四个循环周期，MAE和RMSE 最高值分别为0.0112 和0.0145。而当预测起点为100时，由于数据量增加了，模型精度有了一定程度的提升，AE 值均为0，MAE 和RMSE最高值分别为0.0039 和0.0052。以上实验结果表明，本工作所提出的集成模型在预测起点不同的情况下依旧可以有效预测出电池容量衰退状态。

为了验证本工作提出模型各模块的必要性，在预测起点为80 的条件下，进行了消融实验，消融实验结果如表3所示。

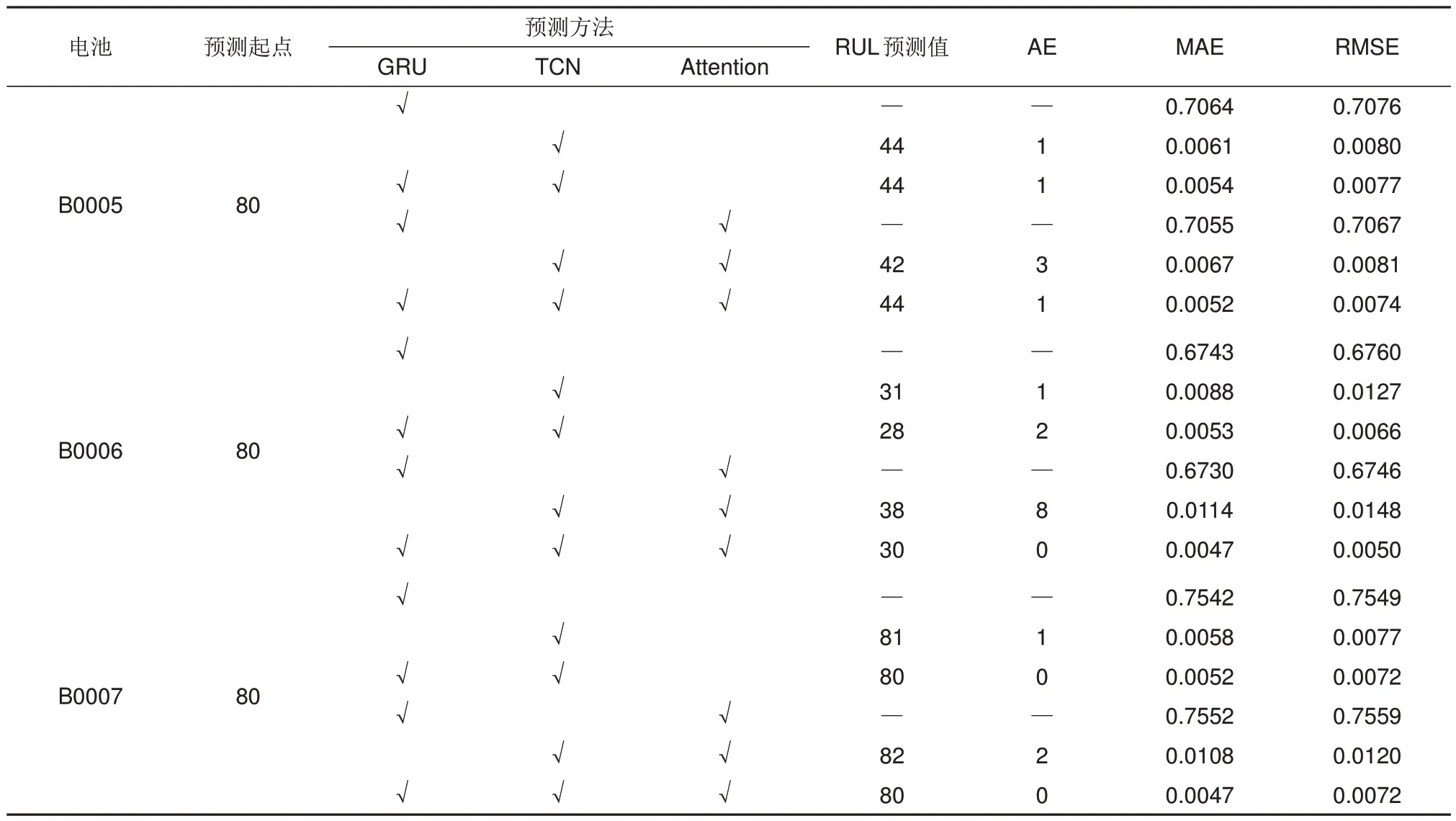
表3 消融实验结果Table 3 Ablation results

由表3 可得，当只使用GRU 对高频分量预测时，模型性能较差，MAE 和RMSE 最大值分别为0.7542 和0.7549，而当只使用TCN 对低频分量预测时，模型性能就有了较大提升，MAE和RMSE最大值分别为0.0088和0.0127，验证了2.2节中所提出的假设：动力电池容量衰退过程中由噪声和容量回升现象导致的非线性特征被分解到高频分量，而原始容量数据的主要趋势被分解到低频分量，且低频分量中不再有噪声及容量回升现象导致的非线性特征，因此当只使用TCN对低频分量进行预测时，预测精度显著高于只使用GRU对高频分量预测。当分别使用GRU和TCN对高频分量及低频分量进行预测，再对预测数据进行叠加重构时，MAE 和RMSE 最大值分别为0.0054 和0.0077，这是由于使用GRU和TCN模型对高频分量和低频分量进行预测时，能够有效捕捉分解后数据的特征信息，证明本工作提出的数据分解模块和时序预测模块能够有效提升模型性能。当使用加权平均集成替代叠加重构对预测结果进行集成后，MAE和RMSE最大值分别为0.0052和0.0074，证明本工作提出的数据重构方法相较于当前主流的叠加重构方法更有利于提升模型精度。以上消融实验结果分析验证了本工作提出模型中的数据分解模块、时序预测模块、数据重构模块在动力电池的RUL预测任务中的必要性。

3 结 论

为了提升动力电池RUL 预测精度，本工作提出了一种多尺度分解下GRU-TCN集成的RUL预测方法，在EEMD 的基础上，使用Attention 对GRU和TCN 模型的预测结果进行加权平均集成得到动力电池的容量衰退状态，从而得出RUL。在NASA数据集下进行了对比试验、消融实验及不同预测起点实验，得到了以下结论：

（1）使用EEMD能够将动力电池容量衰退数据中由噪声和容量回升现象导致的非线性特征和主要趋势分解为不同分量，有效降低了电池容量回升现象导致的非线性特征对预测结果的影响；

（2）使用GRU和TCN 模型对不同的分量进行预测，能够有效捕捉原始数据的总体退化趋势和局部非线性特征，提升了电池容量衰退状态的预测精度；

（3）使用Attention 集成两种网络的预测结果，能够避免直接叠加重构对噪声的放大及各分量间的干扰，得到更稳定的RUL预测结果；

（4）本工作提出的模型相较于典型单一模型和其他同类型模型，最大MAE 和RMSE 分别降低了0.0076、0.0047 和0.0148、0.0046，AE 均为最小值，并且在不同电池数据下AE 波动最小，证明本工作提出的模型能够增加动力电池RUL 预测的准确性和稳定性，可有效应用于动力电池RUL预测。在后续的研究中，可以考虑在多特征分解的基础上，分析多特征之间的耦合关系，进一步提升动力电池的RUL预测精度。