基于卷积Fastformer的锂离子电池健康状态估计

申小雨，尹丛勃

（上海理工大学机械工程学院，上海 200093）

锂离子电池作为一种应用广泛的电能存储技术，具有能量密度高、发电能力强、寿命长等优点[1]。锂离子电池在使用过程中持续放电和充电，随着充放电过程的进行，锂离子电池的性能会逐渐下降。为了确保锂离子电池的稳定性和安全性，准确估计SOH 对于锂离子电池可靠安全运行至关重要[2-3]。

目前，对于锂离子电池SOH 估计的方法主要有模型驱动法和数据驱动法。对于基于模型的方法，必须基于先验知识或物理定律建立电池的退化模型，这些模型可以进一步分类为电化学模型(electrochemical model，EM)[4]、等 效 电 路 模 型(equivalent circuit model， ECM)[5]、 滤 波 模 型(filtering model，FM)[6]和随机过程模型(stochastic process model，SPM)[7]。为了研究EM 和ECM 的化学或物理特性及工作原理，必须进行电池老化分析，需要复杂的建模过程。FM和SPM的目的是挖掘内部电池状态的递归关系或电池监测数据的变化规律[8]。然而，由于内部机制和外部操作之间的相互作用，这些方法表现出动态精度低、适应性有限和先验知识不足的缺点。

相比之下，数据驱动法可以根据电池的电流、电压和温度等参数估计SOH，而不需要对电池内部复杂的电化学机理进行精确建模。可以很容易地为特定应用构建高精度模型[9]。Goh等[10]通过高斯过程回 归(Gaussian process regression， GPR) 估 计SOH。Xing 等[11]提出了天鹰优化（aquila optimizer，AO）支持向量机(support vector machine，SVM)核心参数的预测方法，实现SOH 估计，但基于启发式算法超参数的确定运行时间较长且有可能陷入局部最优解。上述这些传统方法在电池老化数据具有高度非线性特性的情况下精度较低[12]。Chen等[13]利用长短期记忆(long short-term memory，LSTM)神经网络进行容量估计。高德欣等[14]提出了卷积神经网络(convolutional neural network，CNN)与双向长短期记忆网络融合模型用于SOH 估计，两种网络结构在数据处理的不同阶段各自发挥重要作用。但是基于循环神经网络(recurrent neural network，RNN)结构的神经网络存在长期依赖性问题，影响预测性能。Transformer 模型具有更好的全局信息感知能力和更强的表达力，可以更好地捕捉充放电数据中的时间依赖性和SOH的变化趋势。陈锐等[15]采用Transformer 对锂电池SOH 进行估计，具有较高精度，但是，由于Transformer 中的自注意力机制的二次复杂度使得它在长序列建模中效率低下。

数据驱动方法的估计精度不仅取决于估计算法，还取决于提取的健康特征(health feature，HF)。近年来，从电池充放电曲线中提取特征进行SOH 估计引起了越来越多的关注，但放电状态不稳定，放电过程主要取决于使用环境和工作条件。相比之下，从充电曲线中提取特征更稳定、更容易[16]。一般通过从电压、电流和温度等变量中提取的特征来估计SOH[17]。Jia 等[18]从恒流充电电压曲线中提取HF，还计算了提取的特征与电池SOH之间的皮尔逊相关系数进行数据降维，以免特征的高维度导致过度拟合并影响估计的准确性。总结统计数据可以有效地以数字方式说明电压曲线的形状和位置变化[19]，Zhu 等[20]从充电弛豫阶段提取电压统计特征，结合XGBoost实现较高的容量估计精度。

基于上述文献启发，本工作采用统计学方法从充电阶段提取HF，采用皮尔逊相关系数降维方法消除特征的冗余性。针对上述模型存在的问题，建立了一种卷积Fastformer 模型进行SOH 估计，卷积可以更好了解输入特征的局部信息，提高预测精度，Fastformer 的线性复杂度比Transformer 复杂度低[21]，可更高效地在复杂的长序列中总结全文信息，同时利用Fastformer的附加注意力机制可以弥补RNN、LSTM等网络以循环方式对序列数据进行建模时，由于长期依赖而降低性能的缺陷。为了快速优化模型超参数，使用正交实验法找到最优参数。

1 多级充电策略分析及特征提取

1.1 实验数据

基于数据驱动方法的电池寿命预测，Severson 等[22]通过大量的组合实验收集电池数据。该数据集包括124 个商用LiFePO4石墨电池。电池的标称容量为1.1 Ah，其上限截止电压和下限截止电压分别为3.6 V和2.0 V。所有电池都在环境温度为30 ℃的恒温温箱内循环，直到其容量降至标称值的80%以下。本工作选取了第三批数据在通道11、12、13、14 上测得的电池数据，分别命名为B01、B02、B03、B04，图1 为 电 池 容 量 衰 减曲线。

图1 电池容量衰减曲线Fig.1 Battery capacity decay curve

1.2 充电过程

对于车辆应用，使用典型的恒流恒压(constant current-constant voltage，CC-CV)充电协议。充电过程在实际运行中一般由几个子过程组成：CC和CV。在实际中，为了快速充电和延长电池寿命，通常使用多级充电策略。多级充电策略包括多级恒流充电和恒压充电，可表示为“C1(Q1)-C2”，其中C1 和C2 分别是第一和第二阶段的电流速率，Q1为两阶段电流速率切换时的电池荷电状态(state of charge，SOC)。充电策略不同，Q1 也不同。CC2 阶段恒流充电至SOC 80%结束，之后用1 C的“恒流-恒压”模式对电池进行充电，本工作中1 C等于1.1 A，4个电池具体规格参数如表1所示。图2 显示了一个示例，充电电流速率首先恒定为5.6 C，在SOC 值达到Q1 后，充电电流速率切换到另一个恒定的4.3C，在SOC达到80%后，充电电流速率切换到另一个恒定的1 C充电至电池最大截止电压3.6 V结束。之后，电池以3.6 V的恒定电压以电流递减的方式充电，当电流速率为0.02 C时停止充电。电压曲线清楚地表明了严重的非线性。

表1 实验电池规格参数Table 1 Experimental battery specifications

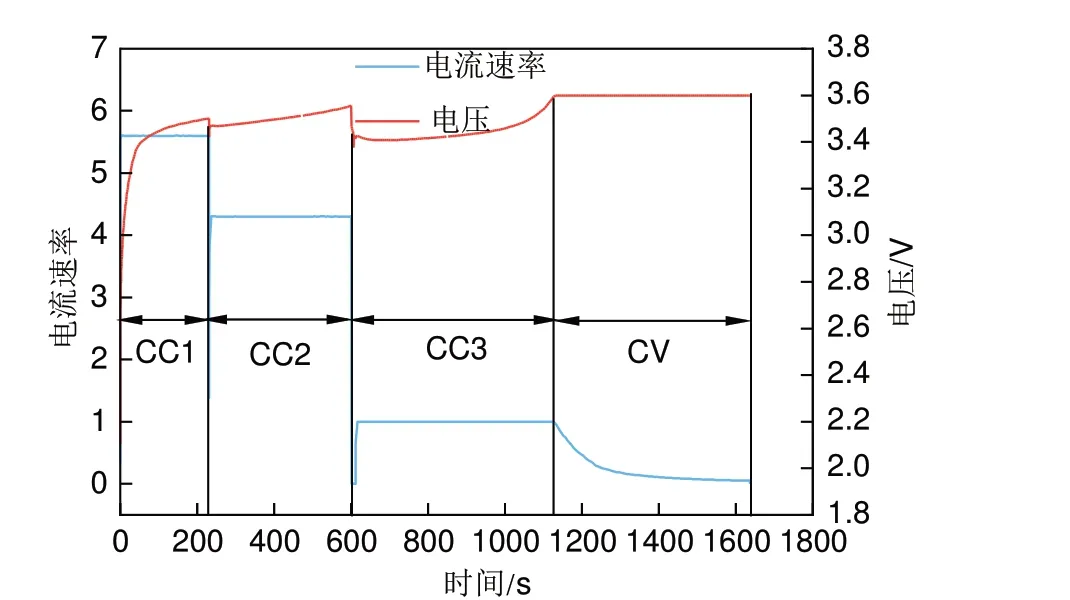
图2 充电过程Fig.2 Charging process

1.3 健康特征提取

对充电过程中的多级恒流充电阶段电压曲线和恒压阶段电流曲线进行特征提取，当电池循环数变化时，电池将具有不同的特性。因此，不同循环次数的电池，其内部性能和外部性能会有所不同，从而导致充电时的各个循环周期的电压、电流曲线形状不同。图3所示为电池在四个不同循环次数下的充电电压曲线。充电的持续时间和电压达到上限截止电压的时间在不同的循环数下都是不同的。如图4(a)～(c)所示，CC1 阶段的终止电压随着循环次数的增加呈上升趋势，CC2、CC3阶段的起始电压和终止电压随着循环次数的增加都呈上升趋势。如图4(d)所示，CV 阶段的起始电流速率和终止电流速率随着循环次数的增加呈下降趋势。

图3 不同循环充电电压曲线Fig.3 Curves of different cycling charging voltages

图4 不同循环充电曲线Fig.4 Charging curve of different cycles

统计数据能够准确用数字方式说明电压曲线的形状和位置变化，因此在恒压、恒流阶段进行特征提取时，每个阶段各个曲线转换为6 个统计特征，即方差(Variance)、偏度(Skewness)、最大值(Max）、 最 小 值(Min)、 均 值(Mean) 和 峰 度(Kurtosis)。由于CC3阶段的最终电压为截止电压，所以在处理CC3 阶段的电压数据时，每个循环采集到的数据只取其中的10%～90%。同时为了避免CC2 阶段每个循环提取到的电压最小值和CC1 阶段每个循环提取到的电压最大值有重合，处理CC2阶段的电压数据时，每个循环采集到的数据只取其中的10%～90%。数据驱动模型的输入特征和输出之间的相关性越高，模型的准确性就越好。采用Pearson相关系数(ρ)来衡量各曲线统计特征和电池容量两者的关系，公式(1)如下：

式中，xj是特征序列，y是电池容量，-xj、-y是其平均值。

如图5所示，CC1阶段的电压最大值、CC2阶段的电压最小值、CC3阶段的电压最大值这三个特征的Pearson 相关系数绝对值接近于1，与电池容量存在较强的相关性，最终选定这三个特征。图6所示为3个特征分别与电池容量的对应关系，可以明显看出在各个循环中，CC1 阶段电压Max 值、CC2 阶段电压Min 值和CC3 阶段电压Max 值分别与电池容量都表现出明显的单调相关性。

图5 充电过程统计特征和容量的相关系数Fig.5 Correlation coefficient between charging process statistics and battery capacity

图6 恒流充电阶段电压与容量关系Fig.6 Relationship between constant current charging stage voltage and battery capacity

2 基于卷积Fastformer的锂离子电池SOH估计

2.1 Transformer

Transformer[23]被提出作为一种全新的架构，它利用注意力机制来处理一系列数据。标准的Transformer 是一个序列到序列的架构，编码器获取输入数据并将其映射成更高维向量，然后送入解码器生成输出。与基于RNN 的方法不同，Transformer 中不同的注意力头会关注特征的不同方面。这些使Transformer在预测方面有明显优势。Transformer 在一个多头自注意层中，同时将输入Y转化为H个不同的查询矩阵Qh、键矩阵Kh和值矩阵Vh，公式如下：

式中，h=1…H，W Q h、W K h和W V h是可学习的参数。

在经过线性变换之后，输出缩放的点积注意力：

式中，dk为缩放因子，Oh为第h头注意力输出结果。

之后，O1,O2,…,Oh被连接起来并经线性变换。

Multihead(Q，K，V)= Concat(O1，O2，…，Oh)W O(6)

式中，W O为可学习的参数。

2.2 卷积Fastformer

卷积Fastformer模型如图7所示，通过采用内核大小为k且步幅为1的一维卷积，将输入转换为查询矩阵Q和键矩阵K，值矩阵V可以更好了解局部形状，表示为Q=[q1,q2,…,qn],K=[k1,k2,…,kn],V=[v1,v2,…,vn]，Q,K,V∈ℝN×d，其中N为序列长度，d为隐藏维数。

图7 卷积Fastforme模型结构Fig.7 Convolutional Fastforme model structure

由于Transformer 的点积注意力机制的二次复杂度使得它在长序列建模中效率低下。Fastformer中附加注意力是注意力机制的一种形式，可以更高效地在线性复杂的序列中总结重要信息，附加注意力模型如图8所示。附加注意力首先将查询矩阵概括为全局查询向量q∈ℝd，该向量压缩了查询矩阵的全局上下文信息。第i个查询向量的注意力权重αi计算如下：

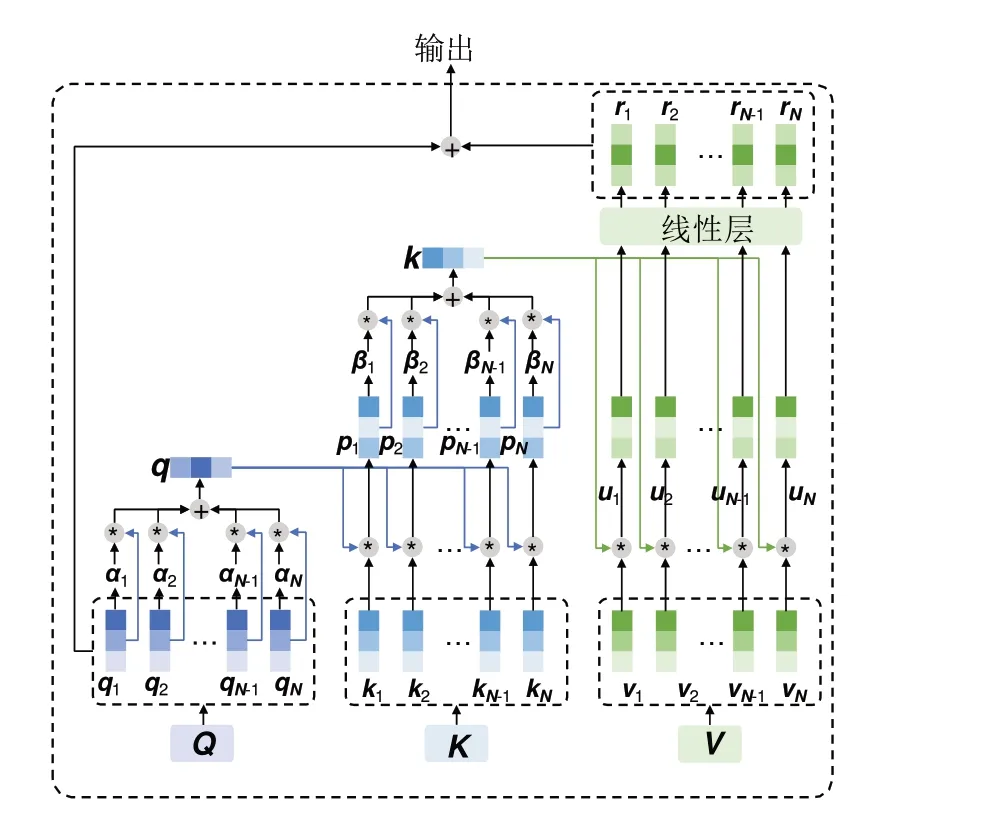
图8 附加注意力Fig.8 Additive attention

式中，wq∈ℝd是可学习的参数向量。

全局注意力查询矩阵计算如下：

使用全局查询向量和每个键向量之间的逐元素乘积得到全局上下文键向量：

使用附加注意机制来总结全局上下文感知键矩阵，其第i个向量的附加注意力权重计算如下：

式中，wk∈ℝd是可学习的参数向量。

全局注意力键矩阵计算如下：

之后，对注意力值矩阵和全局键向量进行建模：

最后，将线性变换层应用于每个键值交互向量以学习其隐藏表示。该层的输出矩阵表示为R=[r1,r2,…,rn]∈ℝN×d。该矩阵进一步与查询矩阵相加，形成附加注意力的最终输出。

2.3 SOH估计流程

该方法的流程如图9所示，主要步骤如下：

图9 SOH估计框架Fig.9 Framework for state of health stimation

（1）数据处理：提取恒流充电阶段电压数据，计算出CC1 阶段的电压最大值，CC2 阶段的电压最小值，CC3阶段的电压最大值作为模型的输入特征向量X=[U1,U2,…,Un]∈ℝL×3，其中L为输入步长。将B02划分为训练集进行模型离线训练，B04划分为验证集进行模型参数优化，B01、B03 划分为测试集进行在线估计。在数据预处理阶段还需要进行归一化处理，以保证数据被限定在同一范围，避免不同取值范围影响模型参数更新。使用Maxmin归一化方法。计算过程如下：

式中，x和x'分别是特征向量S归一化前后的数值。

（2）模型超参数选定：通过正交实验确定模型的输入步长、卷积核尺寸大小、头数、网络深度参数。

（3）模型训练：从第(2)步中获取参数搭建网络结构。将特征向量输入到一维卷积中以获得具有局部特性的Q，K，V。使用附加注意力进一步汇总为全局查询向量、键向量，然后，对全局上下文感知键和值进行交互建模，以学习全局上下文感知的注意值，然后将其与查询向量进行结合，形成输出，使得线性复杂度的Fastformer模型可在复杂的长序列中总结全文信息。最后经过线性层输出第n+1 次循环的SOH 值，将该值与真实值计算均方误差，然后通过梯度下降算法和训练集的迭代，实现网络权重和偏置参数的学习，训练模型。

（4）模型参数选定评价：当模型训练结束后，将验证集输入到训练好的模型中输出估计的SOH，将该值与真实值进行评价指标计算，以此来评价模型参数。重复步骤(1)～(4)直至达到设定的正交实验次数。

（5）模型估计：对正交实验进行极差分析确定出最优模型，将验证集、测试集输入到最优模型输出SOH 估计值，将该估计值与实际值通过评价函数进行计算，从而对所提出的锂离子电池SOH 估计模型进行评价与分析。

3 实验验证

3.1 实验设置

实验所用的模型输入特征向量是有3维充电过程特征向量，输出是锂电池SOH 值。采用Adam作为最小化目标函数的自适应优化器，其初始学习率设置为0.0001，每训练30 次，学习率降低至原来的1/10。训练集批量为50，迭代次数设置为100，测试集采用单步滚动预测方法。

为了评价SOH 模型的估计精度，本工作使用均方根误差(root mean square error，RMSE)和平均绝对误差(mean absolute error，MAE)作为评价函数，计算过程如下：

式中，n是循环次数，Creal是实际SOH值，Cprd是估计SOH值。

3.2 模型参数优化

一般神经网络模型包含很多参数需要进行优化。受限于计算机算力和训练时间，正交实验是一种用于搜索模型参数的高效方法[24]。使用正交实验法对模型主要参数进行设置优化，模型结构的主要参数包括卷积核尺寸K、网络深度N、多头注意力机制中的头数H、输入步长L，即电池前L次循环，共计4个参数。如表2所示，以电池B02为训练集，B04 为验证集确定模型参数。设计3 水平4 因素正交实验。以每次实验的RMSE作为估计精度来进行判断。

表2 正交实验设计Table 2 Orthogonal experimental design

极差分析可反映正交实验结果中模型参数对估计精度RMSE 的影响，具体数据见表3。其中A值表示模型参数各水平均值，R值代表极差，即各模型参数水平均值的最大差异。

表3 正交实验极差分析Table 3 Orthogonal experimental range analysis

通过表3分析可得，通过R值可得到四个模型参数对估计精度的影响大小程度为：输入步长>头数>卷积核尺寸>网络深度。极差分析中的A值表示的是单个因子在三个水平上的差异，通过分析得到各个参数因子A值的最小值，可得到最优的参数组合，即附加维度m、卷积核尺寸、头数、网络深度取值分别为20、4、6、3。

3.3 估计结果与分析

卷积Fastforme 模型在电池B01、B03、B04上的SOH 估计结果和相对误差如图10(a)～(c)所示，红色线代表实际SOH 值，蓝色点划线代表估计SOH，估计相对误差保持在0.8%以内，真实值曲线与估计值曲线基本吻合，证明模型有较高的预测精度。为了验证本工作所提算法的预测能力及HF提取的有效性，与RNN、CNN、GRU共计3种现有模型进行对比分析，图10(d)～(f)是不同模型下的SOH估计曲线，可与图10(a)～(c)比较看出卷积Fastformer模型更贴近真实曲线。4个模型SOH估计结果数据见表4，从整体上看各个模型都具有较高精度，证明了提取特征的有效性，卷积Fastformer 模型最大RMSE、MAE 仅为0.25%、0.29%，具有较高的估计精度和鲁棒性。MAE、RMSE评价指标卷积Fastformer模型都优于其他模型，从而证明了卷积Fastforme模型估计精度高。

图10 估计结果Fig.10 Estimation results

图11 是四个不同模型下3 个电池SOH 估计结果误差的平均值，结果显示本工作所提模型的误差均低于3 种现有算法。本工作所提的卷积Fastformer 模型的平均MAE 和平均RMSE 分别为0.14%、0.18%，与次优模型CNN 相比，平均MAE 相对降低了44%，平均RMSE 相对降低了45.45%。

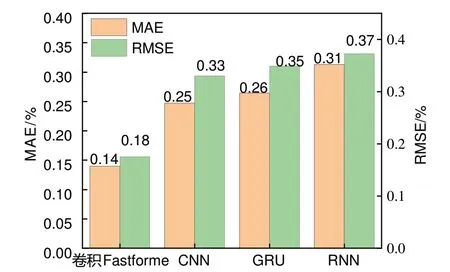
图11 4种模型评价指标平均值对比Fig.11 Comparison of estimation error of four models

4 结 论

为了提高锂电池SOH 估计精度，本工作提出一种基于卷积Fastformer 模型的锂离子电池SOH估计方法，得到如下结论。

（1）通过对充电过程各阶段电压曲线、电流曲线进行统计特征分析，发现利用电压分析方法提取的恒流充电阶段统计特征与电池容量存在强相关性，可以表征电池老化和容量衰减过程。

（2）Fastformer的附加注意力机制可以更高效提取深层特征，使用卷积可更好提取局部信息，进一步提高预测精度。

（3）由于神经网络具有较多的超参数，不同的参数组合，会对预测精度产生较大影响，为了减少算例及训练时间，采用正交实验法对模型超参数进行优化选择。通过公开电池数据集进行实验验证，MAE、RMSE最大仅为0.25%、0.29%，可准确估计锂离子电池SOH。