锈蚀钢材力学性能试验及等效本构模型研究

郑山锁 ，田忠祥 ，杨松 ，穆长俊 ，明铭 ，3

（1.西安建筑科技大学 土木工程学院，陕西 西安 710055；2.西安建筑科技大学 结构工程与抗震教育部重点实验室，陕西 西安 710055；3.中国电力工程顾问集团西北电力设计院有限公司，陕西 西安 710075）

腐蚀会造成钢材的有效截面面积减小并产生应力集中现象，影响其力学性能.张世骥等［1］对经人工锈蚀的Q235 钢板进行了力学拉伸试验，研究发现腐蚀影响钢材抗拉强度、屈服强度的主要原因为其造成试件的有效横截面积减少，同时锈坑处产生的应力集中会造成试件的伸长率大幅降低.郑山锁等［2］对不同腐蚀率的Q235B 钢板进行拉伸试验，发现锈蚀后钢材的力学性能指标随锈蚀程度的增大而显著降低，并通过拟合得到各力学性能指标随平均腐蚀率的退化模型.Wu等［3］、Fu等［4］分别采用最大截面积损失率和钢材浸泡时间表示腐蚀程度，发现钢材延伸率均随着锈蚀程度的增加而大幅下降.Bazán 等［5］对高延性钢筋进行加速腐蚀及拉伸试验，试验显示应力-应变曲线即使在腐蚀程度低于1%的情况下也会产生显著变化.

现有研究主要注重于锈蚀对钢材的单调力学性能的影响，但钢结构在服役期间可能会遭受地震作用.地震对结构施加巨大的往复地震力，材料层面的力学响应与单调荷载相比存在显著差别.薛奇峰［6］对自然腐蚀钢板试件进行循环加载试验，研究发现相较于单调拉伸，循环荷载下部分锈蚀钢材在达到最大强度时发生断裂，延性严重退化.郭宏超等［7］对Q690 高强钢腐蚀试件进行循环加载试验，发现腐蚀100 d 后试件的滞回能降低了15.2%，极限抗拉强度降低了14.6%.上述研究表明，地震所形成的往复荷载与锈蚀的共同作用会进一步加剧钢材性能劣化.而钢材的本构模型是研究钢构件及结构抗震性能的基础，因此需要对锈蚀钢材的循环本构模型进行研究.但现有的研究成果仅分析了钢材在循环荷载与锈蚀的共同作用下会产生性能退化，而对循环本构模型的定量描述相对缺乏.

鉴于此，本文采用经人工加速腐蚀的16 组锈蚀试件，分别进行单调拉伸及循环加载试验，得到锈蚀钢材力学性能及耗能能力在不同锈蚀程度下的退化规律，并通过对其骨架曲线的拟合分析锈蚀对钢材循环强化作用的影响.根据试验结果建立基于Giuffre-Menegotto-Pinto（GMP）的锈蚀钢材循环加载本构模型，并在开源有限元分析平台OpenSEES中对模型中标定的参数进行验证，为今后准确评估和预测锈蚀钢材的抗震性能提供参考依据.

1 试验概况

1.1 腐蚀试验

试验以10 mm 为主要试件，8 mm、12 mm 为对比试件，设计制作了16 组Q355 钢材试件，单调拉伸和循环加载试件各8 组，每组2 个试件.加速腐蚀试验通过湿度控制装置控制室内湿度，参照《金属和合金的腐蚀人造气氛的腐蚀试验 间歇盐雾下的室外加速试验（疮痂试验）》（GB/T 20121—2006）［8］，采用自动喷淋装置对试件进行周期性干湿循环喷雾腐蚀，为确保试件双面锈蚀程度一致，每7 d对试件进行翻面，加速腐蚀试验参数见表1.试验以45 d 为一个加速腐蚀周期，加速腐蚀时长为0～180 d.

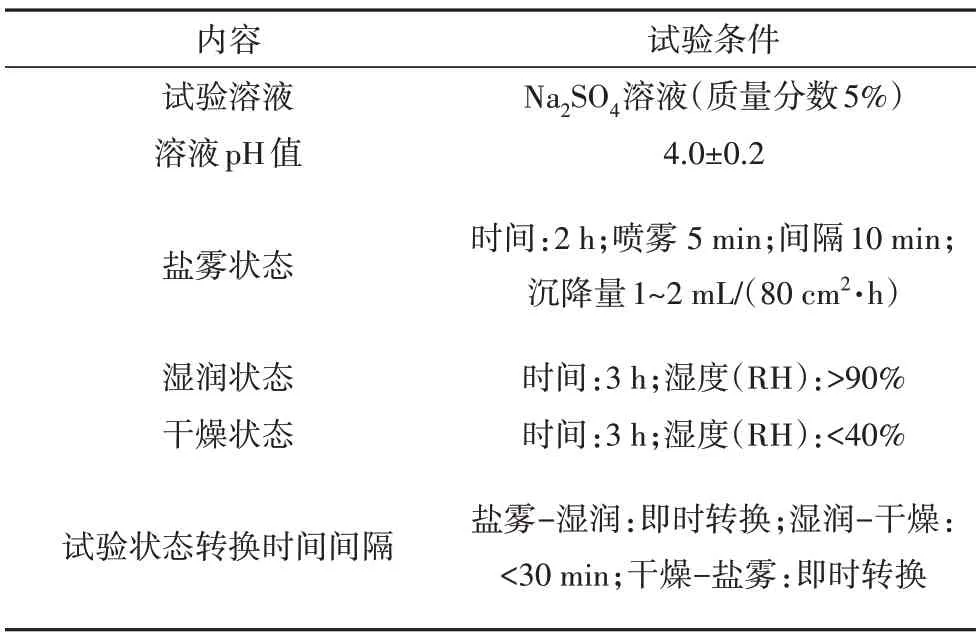
表1 周期盐雾腐蚀试验参数Tab.Parameters of periodic salt spray corrosion test

1.2 加载试验

单调拉伸和循环加载试件尺寸均依据《金属材料 拉伸试验 第1部分：室温试验方法》（GB/T 228.1—2010）［9］设计，试件尺寸如图1 所示，编号规则为：加载类型-钢材初始厚度（mm）-加速腐蚀周期数及组内编号.加载设备采用MTS 250 kN 拉压扭万能疲劳试验机，如图2 所示.循环加载试验采用应变控制加载，参照规范取名义应变速率εv=0.000 25 s-1，单调拉伸和循环加载制度的加载速率分别为1.2 mm/min 和0.45 mm/min.循环加载制度如图3 所示，每级荷载循环两次，观察在相同的应变幅值下不同腐蚀程度钢材的应力强化现象.当应变达到工程常用应变幅值4%后，将试件拉伸至荷载下降为85%峰值荷载即停止加载.

图1 试件几何尺寸（单位：mm）Fig.1 Geometric dimensions of the specimen（unit：mm）

图2 试验加载装置Fig.2 Test loading device

图3 循环加载制度Fig.3 Cyclic loading regime

2 腐蚀结果及分析

2.1 锈蚀钢材表面形貌

通过机械打磨处理试件表面锈层，采用质量分数为12% 的HCl 溶液对试件浸泡除锈，并使用Ca（OH）2溶液中和其酸碱性，随后采用超声测厚仪测量试件的最大残余厚度.图4 给出了不同腐蚀时长下钢材表面的形貌.可以看出，未锈蚀钢材试件表面较光滑.加速腐蚀45 d 的钢材表面覆盖较薄的锈层，除锈后表面可见随机分布的锈坑.随着加速腐蚀时长增加（90～135 d），锈层厚度逐渐增加，表面更加粗糙，除锈后可看出锈坑形状发生不规则变化，锈坑的直径和深度也不断增加.加速腐蚀180 d 的试件，锈层在外力作用下易大面积脱落；除锈后的钢材表面已被锈坑完全覆盖，且锈坑深度较深.

图4 不同加速锈蚀龄期下除锈前后钢材表面形貌Fig.4 Surface morphology of steel before and after rust removal at different accelerated corrosion ages

2.2 锈蚀程度分析

依照锈蚀对钢材力学性能影响的作用机理不同，将锈蚀分为均匀锈蚀与非均匀锈蚀两类.均匀锈蚀对钢材性能的影响主要体现在厚度的削弱，而非均匀锈蚀在钢材截面面积削弱的基础上同时会产生应力集中现象.根据既有研究成果［11］，本文采用非均匀锈蚀参数表示坑蚀对钢材力学性能的影响，表达式为：

式中：ρn为等效非均匀锈蚀参数；Du为均匀锈蚀部分的失重率，可根据钢材试件的厚度获得；Dn为坑蚀部分的失重率；T0和Tmax分别为试件初始厚度和最大残余厚度；Dw为钢材失重率；m0为同组两个试件的初始质量均值；m1为腐蚀后质量.

表2 给出了各钢材试件的宏观锈蚀参数.可以看出，当腐蚀龄期相同时，试件各项宏观锈蚀参数随钢材厚度的增大而降低.锈蚀前期试件的最大残余厚度基本等于其初始厚度，随着锈蚀程度的增加最大残余厚度逐渐减小，试件的失重率及等效非均匀锈蚀参数逐渐增加.对比Dn与Dw可知，坑蚀所造成的质量损失在锈蚀过程中占的比重逐渐降低.由于非均匀锈蚀的高度随机性，相同厚度的试件随着加速腐蚀时长增加，宏观锈蚀参数的离散程度增大.

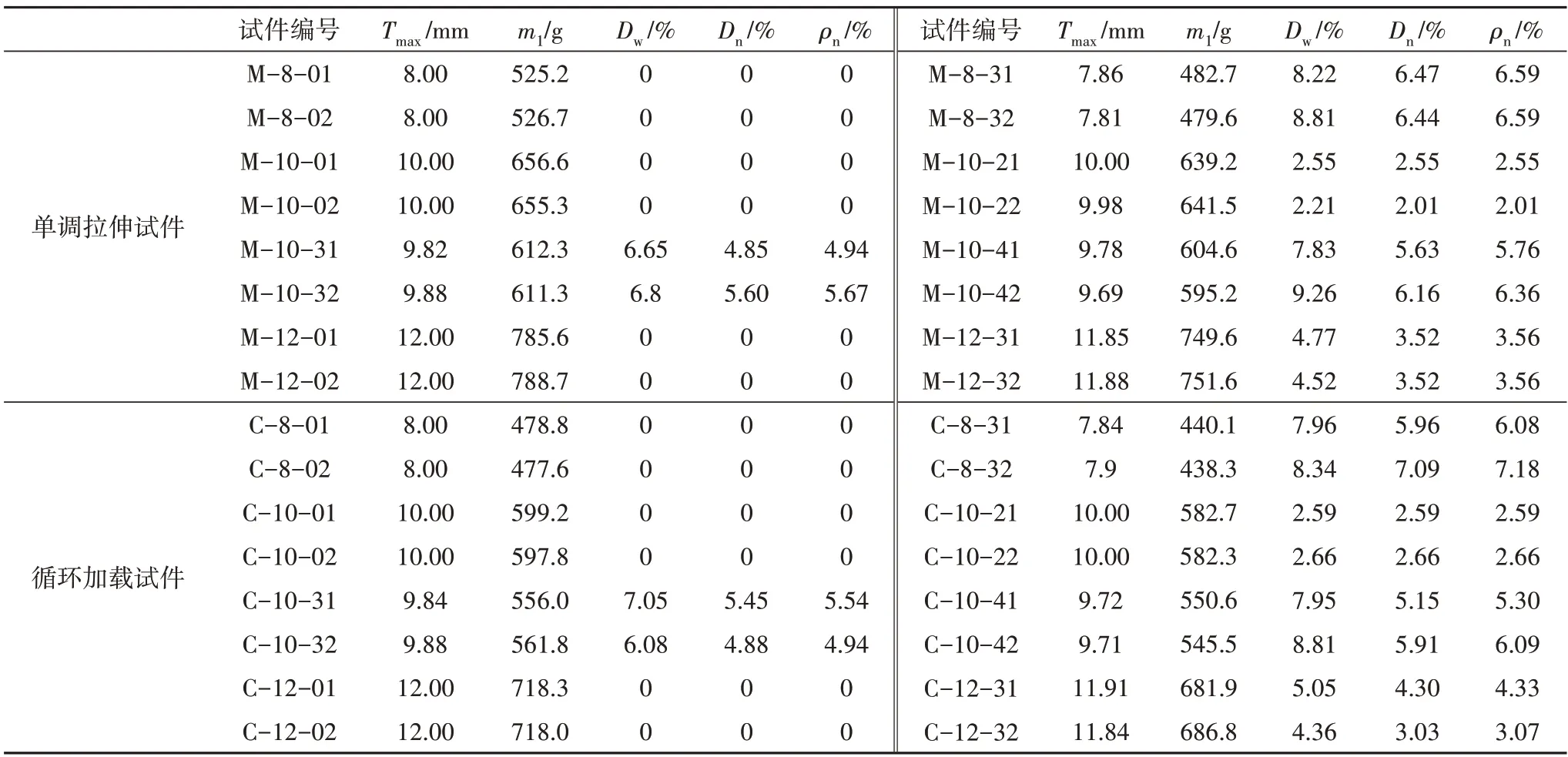
表2 试件宏观锈蚀参数Tab.2 Macroscopic corrosion parameters of the specimens

3 加载试验结果分析

3.1 单调拉伸试验

由于均匀锈蚀对钢材力学性能的影响主要体现在对钢材厚度削弱，而非均匀锈蚀则会引起钢材应力应变集中进而影响力学性能［12］.为描述腐蚀对钢材力学性能的影响，采用最大残余厚度Tmax计算名义应力及应变，分析钢材锈蚀后的力学性能：

式中：σ为试件的应力；ε为试件的应变；F为试验荷载；b为试件平行段的宽度；Lc0为引伸计标距原始长度；ΔLc为引伸计标距伸长量.

图5 与表3 汇总了典型试件在单调荷载下的应力-应变曲线与主要力学性能参数.可以看出，随着锈蚀程度的增加，弹性模量E、屈服强度fy、极限应力fu、极限应变εu以及应力下降到85%极限强度时所对应的应变εu1均逐渐减小.同时由于非均匀锈蚀所造成的试件有效截面面积减小以及应力集中使得曲线中屈服平台逐渐缩短［13］且倾角发生变化.

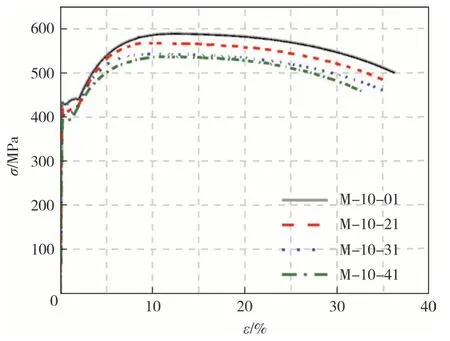
图5 单调拉伸曲线Fig.5 Monotonic tensile curve

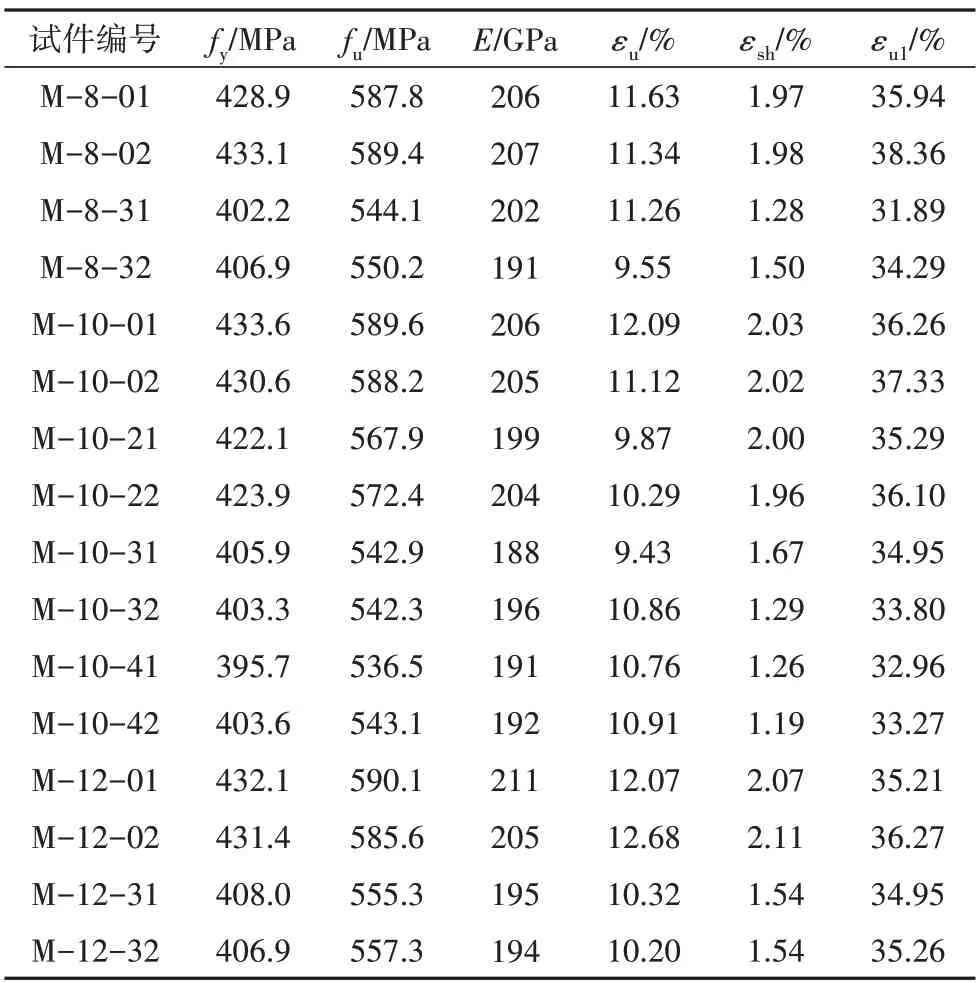
表3 单调荷载试件力学性能指标Tab.3 Mechanical properties of monotonic load specimens

为定量分析非均匀锈蚀对钢材力学性能的影响，以等效非均匀锈蚀参数ρn为自变量分别对锈蚀钢材试件弹性模量、屈服强度、极限强度进行回归分析，分析结果如图6 所示.图中fy0，fu0，E0为同组未腐蚀试件对应参数的均值，R2分别为0.66、0.90、0.94.可以看出，等效非均匀锈蚀参数对腐蚀试件力学性能有较好的拟合，并得到了钢材力学性能随等效非均匀锈蚀参数的退化规律.

图6 力学性能退化规律Fig.6 Degradation law of mechanical properties

3.2 循环加载试验

3.2.1 滞回能力

图7 和表4 分别给出了循环荷载作用下典型试件的应力-应变曲线及力学性能指标.部分试件由于几何尺寸、应力不均匀等因素［14］在受压应变较大时产生局部屈曲变形，试件平行段的形状由直线型变为折线形，如图8 所示，滞回曲线上表现出受压软化现象.随着锈蚀程度增加，钢材各项力学参数呈下降趋势.试件在加载过程中遵循等向强化和随动强化效应，加载前期强化程度较高，后期逐渐减小.对比不同腐蚀时长、不同厚度试件的滞回曲线，各锈蚀龄期试件的滞回曲线都较饱满，但滞回环面积随着锈蚀程度增加而逐渐减小，说明锈蚀对钢材滞回曲线形状特征的影响并不明显，同时反映出Q355 钢材虽具有较好的耗能能力，但其耗能能力在锈蚀损伤影响下会逐渐下降.

图8 试件屈曲Fig.8 Specimen buckling

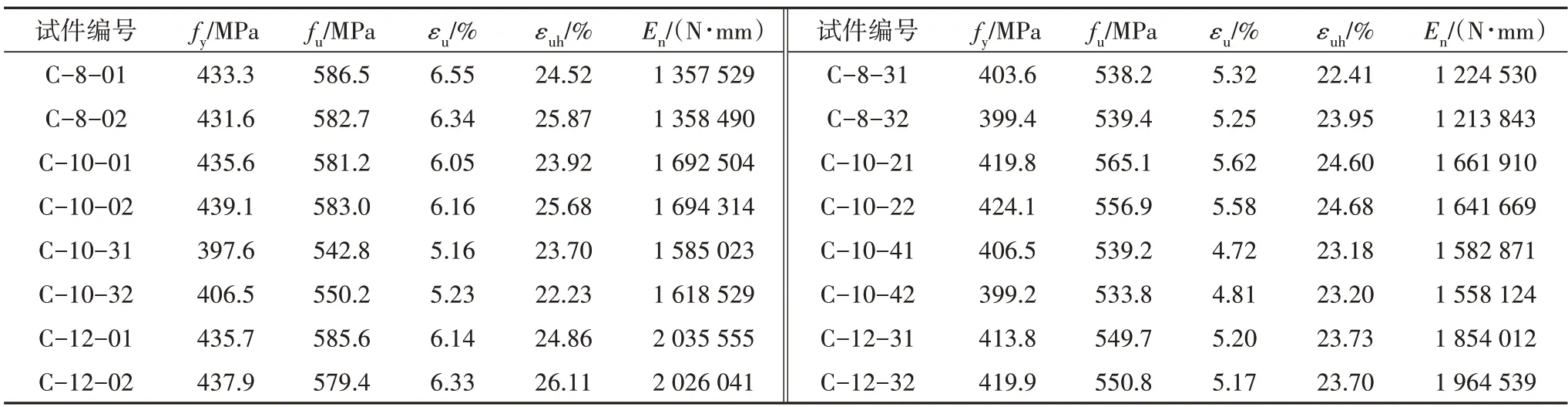
表4 循环荷载试件力学性能Tab.4 Mechanical properties of cyclic load specimens

图9 对比了相同腐蚀程度钢材在单调荷载及循环荷载下应力-应变曲线.可以看出钢材在单调加载与循环加载下的应力-应变曲线明显不同，循环加载前期钢材的强化效应更加明显.同时由于循环加载造成的损伤累积效应使得试件的强度提前降低，应力下降至85%峰值应力时对应的应变εuh大幅减小［15］.图10对比了不同锈蚀程度钢材的耗能行为，可以看出锈蚀会降低钢材的耗能能力.随着锈蚀程度的增加，钢材的耗能能力呈线性退化趋势.

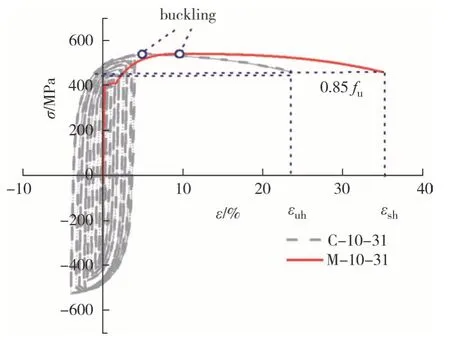
图9 单调和循环加载试件曲线对比Fig.9 Comparison of curves between monotonic and cyclic loading specimens

图10 腐蚀前后钢材的耗能行为Fig.10 Energy consumption behavior of steel before and after corrosion

3.2.2 骨架曲线

采用Ramberg-Osgood 模型［16］对各循环加载试件的骨架曲线进行拟合，并与其对应的单调加载曲线进行对比，对比结果如图11 所示.由图11 可以看出，钢材在循环加载下的骨架曲线屈服平台消失，钢材硬化更明显，屈服后骨架曲线的应力高于单调加载曲线.对比不同腐蚀程度的拟合曲线与单调拉伸曲线可知，锈蚀会降低钢材的循环强化效应.图12给出了循环强化参数随锈蚀程度变化的趋势.随着钢材锈蚀程度的增加，钢材的循环强化系数K'逐渐降低，钢材循环强化指数n'较为稳定.

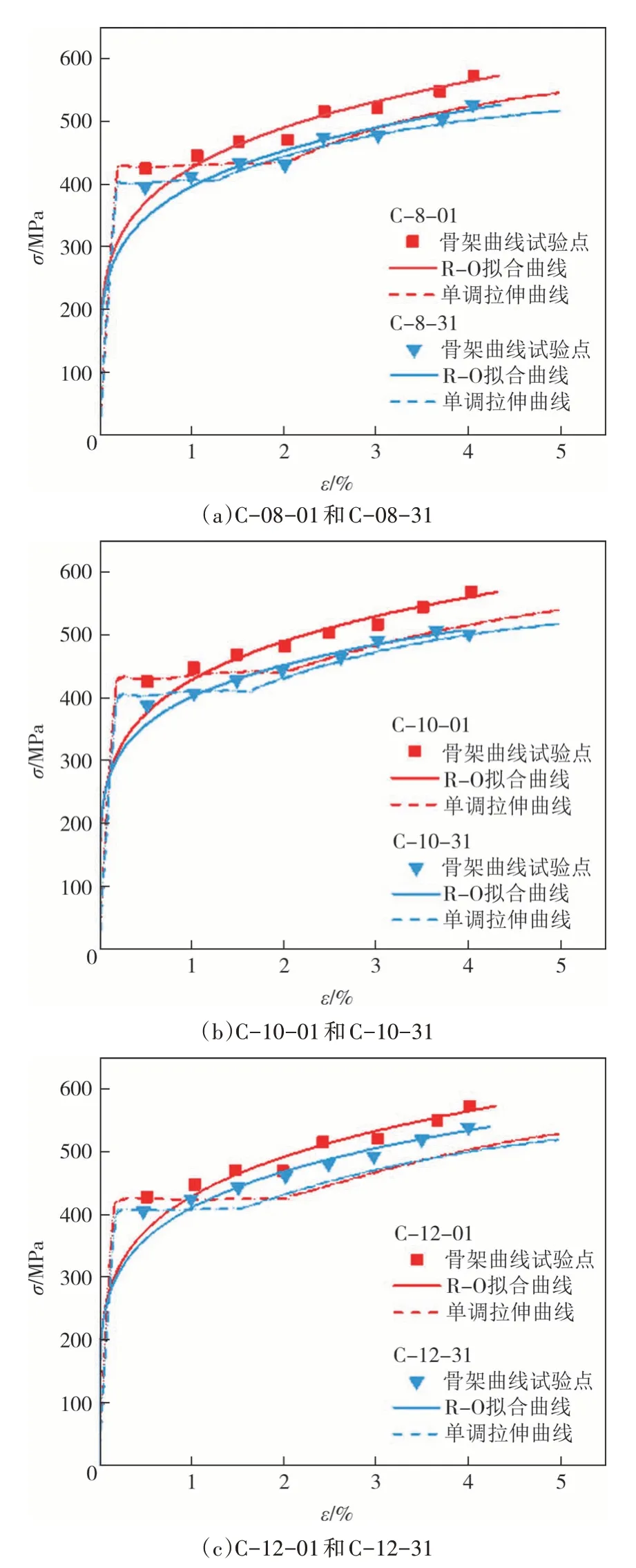
图11 锈蚀钢材循环骨架曲线与单调曲线对比Fig.11 Comparison of skeleton curve and monotonic curve of corroded steel cycle

图12 循环强化参数拟合结果Fig.12 The fitting results of cyclic strengthening parameters

4 锈蚀钢材等效循环本构模型研究

4.1 钢材循环本构模型

基于第3 节分析结果，可以看出锈蚀钢材在单调荷载与循环荷载下的本构关系差异很大，在循环荷载下钢材等向强化和运动强化效应更加明显，运用单调荷载下的本构模型无法准确描述钢材在循环荷载下的力学行为.Chaboche 和Giuffre-Menegotto-Pinto 等模型均可以考虑材料的各向同性和运动硬化.其中Giuffre-Menegotto-Pinto 模型参数较少，求解稳定，模拟精度高，对计算水平要求较低，且已在开源有限元分析平台OpenSEES 中作为STEEL02 模型实现.因此选择基于Giuffre-Menegotto-Pinto 模型建立钢材锈蚀后的循环荷载滞回响应.

Steel02模型由公式（7）表示，模型由两条渐近线和一条过渡曲线构成，应力应变关系如图13（a）所示，一条渐近线斜率为E0，另一条渐近线取斜率为E1=b·E0，两条渐近线在每一循环下不断更新.模型表达式如下：

图13 Steel02模型（Giuffre-Menegotto-Pinto 模型）Fig.13 Steel02 model（Giuffre-Menegotto-Pinto model）

式中：σ*和ε*分别为正则化应力和应变值；b为应变硬化率；R为控制曲线形状和Bauschinger 效应的参数；σr和εr分别为每级循环开始反向加载时的应力及应变；σ0和ε0分别为每级位移下弹塑性段渐近线交点处的应力及应变；

为了进一步完善Menegotto 和Pinto模型，采用弹塑性段曲线渐近线的偏移值来表示等向强化效应，如图13（b）所示，每级循环下受压和受拉方向的屈服偏移值σst为：

式中：εpmin和εpmax分别为每级循环下的最小应变及最大应变；a1及a2为控制钢材受压方向等向强化的参数；a3及a4为控制钢材受拉方向等向强化的参数.

4.2 参数确定

Steel02模型需要确定的参数主要分为4类：

1）实测参数.包括各试件的屈服强度fy、初始弹性模量E0及应变硬化率b.

2）弹塑性过渡段曲率控制参数.Carreño 等［17］对R0和C1分别取了4 种组合，通过滞回曲线的差异度以及COV 值，认为R0与C1可取常数，以此简化参数校准过程，通常取默认值即R0=20，C1=0.925.

3）等向强化参数.根据式（11）及式（12）可以看出，对于每个加载方向可由单一参数定义：拉伸和压缩分别为a3/（a4）0.8和a1/（a2）0.8，同时由于各向同性硬化与a1和a3直接相关，可将参数a2和a4的值设为1.因此，模型中的4 个各向同性硬化参数可简化为两个自变量.

4）初始应力值.取默认值siglnit=0.0.

4.3 锈蚀钢材滞回本构校验

首先计算循环加载试件在受压、受拉方向屈服后的偏移值σst，进而通过式（11）与式（12）确定受压及受拉方向的等向强化控制参数a1与a3；由于部分试件在加载过程中发生了屈曲现象，但屈曲在小应变下对试件受拉方向强度影响可以忽略［18］，因此采取小应变的曲线及受拉方向的加载峰值点进行模型参数计算与校验.对部分循环加载试件的单轴模型进行数值模拟，在已确定其他参数前提下，通过调整单轴本构模型，使其与各钢材试件的试验滞回曲线更加贴合，得到模型的曲率控制参数c2.

表5 汇总了初始厚度为10 mm 试件的应变硬化率及等向强化效应控制参数计算结果和曲率控制参数的校验结果.可以看出，应变硬化率虽随着锈蚀程度逐渐降低但幅度较小，这与Ramberg-Osgood 模型对循环骨架曲线的拟合结果中循环强化指数变化较为稳定的规律一致.受压方向等向强化参数明显大于受拉方向等向强化参数，这是由于受压时试件截面面积增大，受拉时截面面积减小.不同锈蚀程度下试件的各参数未发生较大的变化，也验证了非均匀锈蚀对滞回曲线形状的影响并不明显，故对于等向强化参数取均值，曲率控制参数建议取0.13～0.17.

表5 Steel02模型参数计算及校验结果Tab.5 Steel02 model parameter calculation and verification results

以上述得到的初始厚度为10 mm 的各参数建议值分别拟合其他厚度试件滞回曲线，如图14 所示，拟合结果与试验数据较为贴合，表明通过试验研究得到考虑钢材锈蚀的Steel02本构模型能够较准确地模拟循环荷载下锈蚀钢材的滞回响应.由于Steel02本构模型不能反映钢材受压产生的屈曲软化现象，部分试件加载至应变较大时二者在受压方向存在一定的偏差.

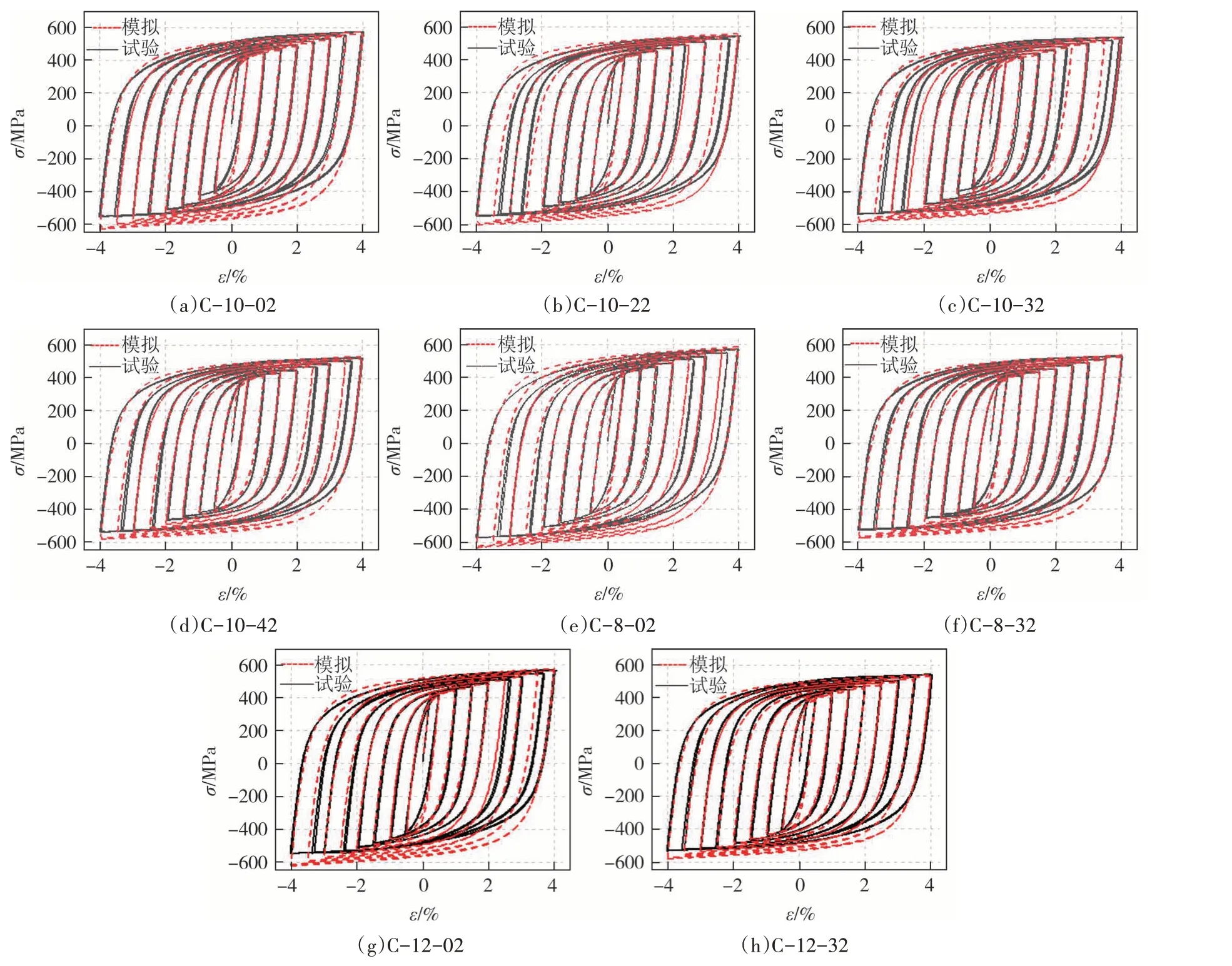
图14 GMP模型模拟结果与试验结果对比Fig.14 Comparison between simulation results and test results of GMP model

5 结论

1）钢材的锈蚀过程主要表现为锈坑产生、扩展并融合、完全覆盖钢材表面并造成厚度削弱.当锈蚀龄期较短时，钢材锈蚀仅包含坑蚀.随着锈蚀龄期增加，锈坑的直径和深度不断增加，钢材的最大残余厚度普遍小于初始厚度.对比均匀锈蚀，坑蚀在钢材锈蚀中所占的比重逐渐减小.

2）单调荷载下，钢材的力学性能及变形能力随着锈蚀程度的增加而降低，主要表现在：①屈服强度逐渐降低，屈服平台逐渐缩短；②峰值应力逐渐降低，且峰值应力对应的应变减小；③应力下降至85%极限强度时对应的极限应变逐渐降低；④弹性模量逐渐减小.

3）随着锈蚀程度增加，钢材各项力学参数呈下降趋势.各锈蚀龄期试件的滞回曲线均较饱满，但滞回环面积随着锈蚀程度增加而逐渐减小，表明Q355钢材虽然具有较好的耗能能力，但其耗能能力在锈蚀影响下仍会下降.Ramberg-Osgood 模型对各锈蚀程度试件的骨架曲线均有较好的拟合，且随着钢材锈蚀程度的增加，钢材的循环强化系数K'逐渐降低，但循环强化指数n'较为稳定.

4）模型参数测定及校准结果表明，Steel02 模型较准确地模拟循环荷载下锈蚀钢材的等向强化和随动强化，但由于无法考虑钢材发生弹塑性屈曲而表现出的受压软化，故滞回曲线在受压方向存在一定的偏差.