基于失稳模量理论的降雨条件下非饱和边坡流滑与滑移失稳机理研究
冯学茂 ,刘敏 ,宋祉辰 ,赵炼恒 ,2,3†,林宇亮
[1.中南大学 土木工程学院,湖南 长沙 410075;2.重载铁路工程结构教育部重点实验室(中南大学),湖南 长沙 410075;3.湖南省轨道交通工程结构防灾减灾重点实验室(中南大学),湖南 长沙 410075;4.广西新发展交通集团有限公司,广西 南宁 530029]
降雨入渗会导致土体抗剪强度降低[1-2],引起山体滑坡,给国民经济和人身财产安全带来极大的威胁.近几十年来,气候变化的不确定性以及人类对大自然的开采使得灾难性滑坡事件愈发频繁地发生.许多经典滑坡案例表明,在滑坡事件中通常发生有限滑移破坏和快速流动破坏(流滑)共存的情况[3-4],特别是后者,由于其破坏力强、发生速度快、波及范围广且常常难以预料,因而越来越受到人们的关注[5-8].
边坡失稳是其内部土体发生破坏后的最终表现.该过程通常与土层内滑动面的产生有关,从力学角度看,这意味着形成一个剪切应变集中的狭窄带[9],而这种局部化失稳的形成过程可以凭借确切的数学条件进行描述,并可通过适当的本构模型予以预测[10].近几十年来,涌现出了许多理论模型用来预测和解释上述滑坡的发生及其触发机理[11-16].然而,绝大多数模型无法模拟土体液化导致的流体加压现象以及非饱和土的水力耦合效应.对于快速流动滑坡破坏模式,其内部局部土体往往易发生由固态到液态的相转变,即发生所谓的“静态液化”现象[17].无论是饱和土边坡的剪切扰动还是非饱和土边坡的降雨入渗,根据其内部土体所经受的边界条件(即排水条件和不排水条件)不同,边坡的失稳模式亦有所区别:对于存在潜在液化能力的土质边坡,其在不排水条件下触发液化所需的载荷扰动(Δτliq,Δswc)通常要远小于在排水条件下所需的达到临界状态所需的荷载扰动(Δτsf,Δssf).以上现象说明有必要借助合适的边坡失稳准则来判断和区分降雨导致的土体液化和传统的剪切破坏.
本文针对上述可能出现的不同失稳模式开展了降雨条件下非饱和土边坡的渗流稳定性研究.从经典塑性理论出发,引入考虑基质吸力的弹塑性本构模型,利用“失稳模量”的概念建立了相应于不同失稳模式的破坏准则,并详细介绍了理论模型所需各项参数的标定方法;为了验证理论预测模型的正确性,引入了火山灰土的室内水槽试验,预测了火山灰土边坡在不同初始条件下的失稳模式以及失稳时的体积含水率,并将模型预测结果与试验结果进行对比.此外,将失稳模量法与传统的安全系数法相联系,给出了同等条件下基于安全系数法的非饱和土边坡渗流稳定性预测.最后,通过一系列参数分析,探讨了影响非饱和土边坡渗流失稳模式的相关因素,以期为进一步理解非饱和土边坡在降雨条件下失稳后演变成的不同运动模式提供理论依据.值得一提的是,由于非饱和土的降雨入渗过程并不是本文研究的重点,为了简便起见,主要借非饱和土含水率的变化来反映降雨入渗的影响.
1 弹塑性材料的失稳准则
1.1 二阶功理论
在小应变连续力学的背景下,Hill[18]提出了二阶功的概念并由此建立了传统的稳定性准则:
该理论不仅可以较好地描述材料不稳定性状态的扩散效应,还能同应力应变增量响应解的存在性和唯一性联系起来[19-20].在任意给定的应力-应变路径增量下,式(1)大于零,即d2W> 0,意味着材料具有足够的稳定性,同时应力应变增量解具有唯一性.而当d2W< 0 时表明材料处于不稳定状态.因此,二阶功的丧失(即d2W=0)意味着材料将无法承受所施加的扰动,而在数学模型上则体现为本构控制矩阵为奇异矩阵.
1.2 失稳模量
考虑一般形式下的弹塑性材料经受塑性加载,根据经典塑性理论的一致性条件,有:
式中:f(σ',χ)为屈服面函数;df为屈服面增量;σ'为广义有效应力向量;χ则代表与硬化相关的变量.偏导数和分别量化了屈服面随应力和硬化参数的变化.
根据弹塑性理论,弹塑性材料的应变可以分为弹性(可恢复)部分和塑性(不可恢复)部分,即:
式中:δε为总应变增量;δεe和δεp分别为弹性应变增量和塑性应变增量.而当有效应力发生变化时总会相应地产生弹性变形,因此有:
式中:De为弹性刚度矩阵.
结合式(2)、式(3)、式(4)以及非关联流动法则δεp=对于塑性硬化材料在标准应变控制加载条件下的情形,即χ=f(εp),有:
式中:Λ(>0)为塑性乘子,量化塑性应变随荷载增量的变化幅度而变化;g为塑性势函数.其中,硬化模量H可表示为:
于是,式(5)可改写为:
将上式重新调整并合并成含有Λ的项,即可得到:
至此即得到反映总应力与总应变关系的显示公式.从式(8)中不难发现,当HIN→0 时,Λ→∞,此时本构矩阵为奇异矩阵,从试验可控性的角度意味着达到材料的失稳状态,因此也将HIN称为“失稳模量”.
1.3 本构方程
为了推导出失稳模量HIN的显式表达式,现考虑基于广义塑性力学的Cam-Clay本构模型[21]:
式中:τ为剪应力;Mg为达到极限剪切破坏时的摩擦系数(Mg=tanφ');Mf为饱和条件下的抗液化强度(Mf=tanφLIQ,φLIQ为液化摩擦角);为当前屈服面与有效平均主应力轴的交点,即前期固结应力(压力);为使塑性势适应当前应力状态的虚拟变量;σ*为平均土骨架应力,由下式给出:
式中:σnet为法向净应力;s为基质吸力;k为吸力强度系数.
屈服面的硬化法则由其增量形式dσ*Y给出:
式中:rw为控制屈服面在受到浸湿后发生收缩的参数;λ为压缩系数;ξ为破坏时的剪胀系数.
除了力学行为的描述外,该模型还需要反映非饱和土的水文变化规律,即土-水特征模型,用来描述土体基质吸力、渗透率与饱和度的关系.本文考虑Gardner水文模型[22],有:
式中:θres、θsat分别为残余体积含水率和饱和体积含水率;αw为反映进气值的模型参数.
1.4 失稳模式
在降雨条件下的非饱和土边坡中,外界的扰动通常较为复杂,一旦形成土体的不排水条件,则可能在特定的条件下引起土体的液化,进而造成边坡发生流滑[6,23].因此,不同的水力边界条件对于边坡的破坏模式有一定影响.现考虑两种极端情况下的失稳模式:1)模式A,基质吸力控制下的滑移失稳,即排水剪切下的土体失稳;2)模式B,含水率控制下的流滑失稳,即不排水剪切失稳.如图1所示.

图1 无限边坡失稳区周围边界条件示意图Fig.1 Boundary conditions around the unstable zone of an infinite slope
在模式A 中,排水加载假设滑动层边界具有无限大的透水性,因此基质吸力不再受局部应力应变的影响,而仅取决于当前的水力边界条件.在模式B中,假设滑动层边界的渗透性为零,导致剪切过程中产生的超孔隙水压无法消散,基质吸力的变化来自多孔介质的饱和度和变形耦合的共同作用.特别地,由于在不排水失稳(模式B)中,很难直接测得基质吸力的变化率.为此,Buscarnera[24]引入了比水量νw的概念来反映基质吸力的影响:
式中:Fr为土水特征曲线的反函数,即s=Fr(Sr).与失稳模式A不同的是,基质吸力不再仅仅受含水率的变化(dvw)的影响,同时也取决于土体的塑性变形(dεp).
由失稳模量的定义,通过链式法则求导可得上述两种失稳模式下的以及的显式表达式,分别为:
其中,应力比η*由下式定义:
2 理论模型验证——以水槽试验为例
Greco等[25]针对松散火山灰土(临界孔隙度为ncr=0.70)进行了一系列的室内水槽试验,指出土在非饱和状态下的体积塌陷是引起流滑的主要因素之一.本文以上述水槽试验为参考,将模型预测结果与试验结果进行对比来验证理论模型的正确性.
2.1 模型参数标定
参考前人针对当地该类型土的室内试验结果对模型所需的各项参数值予以标定.吸力强度系数k量化了基质吸力对排水抗剪强度的影响,可由直剪试验[26]结果标定得到,如图2(a)所示,通过对数据点进行拟合得到k=0.61;屈服面函数f和塑性势函数g由式(10)给出,其中参数Mf与Mg分别与各自函数的顶点位置有关.通过对排水与不排水三轴试验[7]数据拟合可以标定Mg=0.75(即φ'=37°),Mf=0.47(即φLIQ=25°);硬化参数λ反映屈服面随饱和状态下的塑性应变的变化情况,而rw控制屈服面随吸力值变化,由侧限压缩试验[27]可得λ=0.12,rw=0.04;根据室内水槽试验[25]的土体监测数据,用Gardner 水文模型拟合土-水特征曲线可得模型参数α=0.6.标定后的模型参数汇总见表1.

表1 理论预估模型参数标定汇总Tab.1 Summary of theoretical estimation model parameter calibration

图2 模型参数试验标定Fig.2 Model parameter test calibration
2.2 计算对比结果
表2 为Greco 等[25]对于不同初始状态的火山灰土边坡水槽试验的结果.由表2 可知,对于不同初始孔隙度的样本出现了不同的失稳模式.图3(a)为试验编号为D3 的样本在体积含水率不断增加的情况下其失稳模量的变化.该图表明当考虑模式A,即φ'基质吸力保持恒定的排水条件下时,模型预测当体积含水率θf=0.694 时试验边坡破坏;而当考虑模式B,即当考虑土体的不排水失稳时,模型预测当θf=0.673 时边坡破坏,更接近真实条件下土坡失稳时的体积含水率(θf=0.67),因此模型预测该破坏模式为流滑形式.图3(b)为试验中观测到的D3累计湿润锋(h)以及平均坡表沉降(w).由图可知,当t=20 min时,压力水头发生陡增,与此同时坡表沉降增加,即内部土体发生体积塌陷,有静态液化现象发生,最终演变为流滑失稳.

表2 水槽试验初始条件及试验结果Tab.2 Initial conditions and test results of the flume test
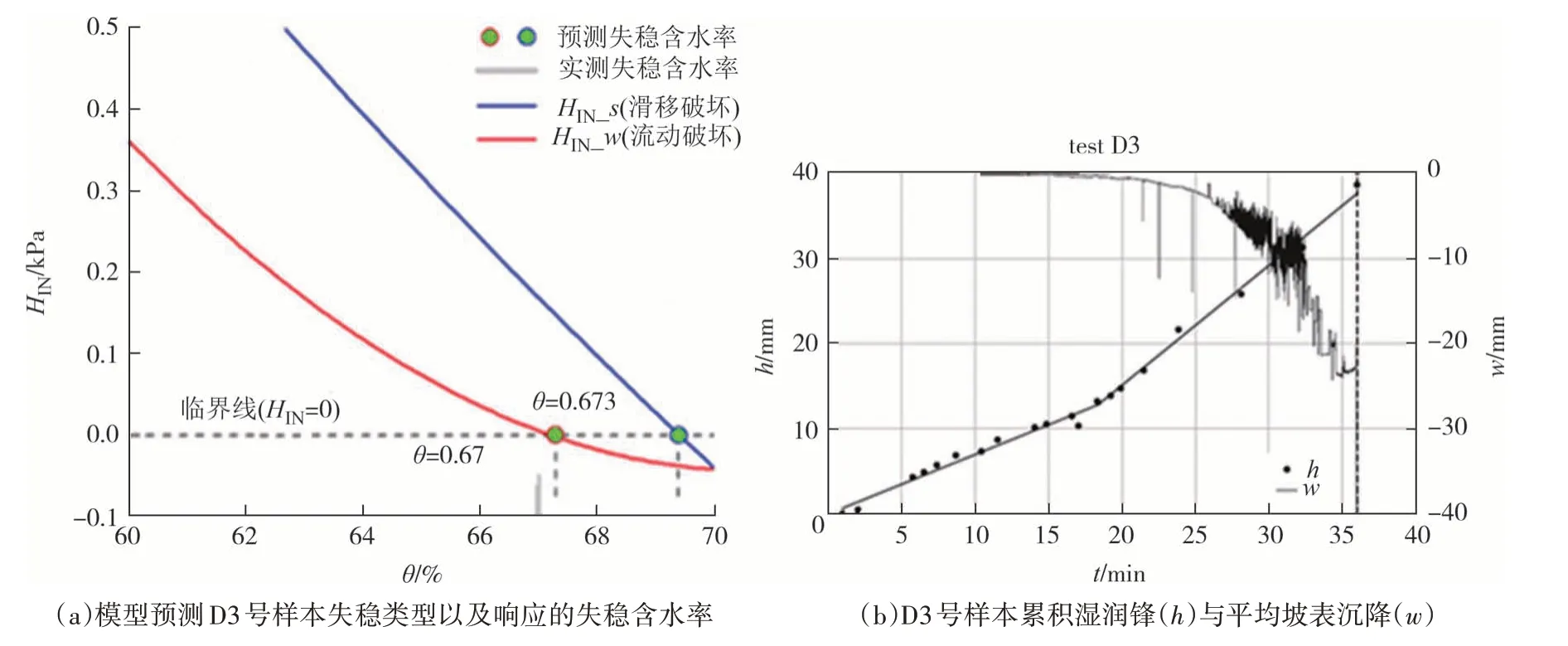
图3 D3号样本失稳模型预测与累计湿润锋及坡表沉降Fig.3 Model predictions of the failure mode,cumulated infiltration height h and mean soil surface settlement w measured during the D3 infiltration experiment
为了进一步说明模型的预测效率,图4 为利用失稳模量法预测其余各组样本出现的破坏形式以及相应失稳时的体积含水率.由计算结果可知,除D9-1 样本外,其余各组均发生失稳.其中D4、D8 失稳后演变为流滑破坏,而D7 的后破坏模式为摩擦滑移破坏,与试验观测结果相符.而就失稳时的体积含水率来说,模型预测结果与试验结果较为接近,其相对误差小于1%,如表3所示.

表3 水槽试验结果与模型预测结果对比统计Tab.3 Comparison and statistics of flume test results and model prediction results
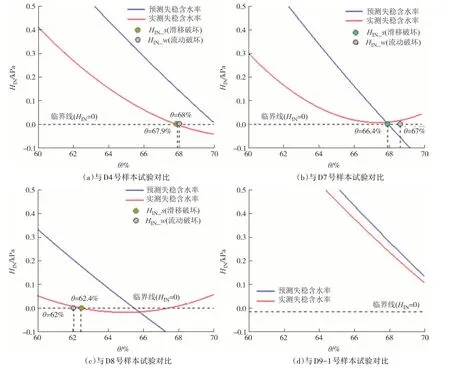
图4 基于失稳模量的模型预测失稳模式及其相应失稳时的体积含水率与实测数据对比Fig.4 Prediction of instability mode based on instability modulus model,comparison of volume moisture content at the corresponding instability with measured data
2.3 安全系数
失稳模量法从机理上解释了非饱和土边坡在不同加载条件下可能出现的不同失稳形式,而在岩土工程领域中,常通过安全系数来评估土体或边坡的稳定性.对于无黏性土的无限边坡模型而言,其安全系数可定义为当前应力比与临界应力比的比值[28-29],即:
式中:β为边坡坡度为临界应力比;rw为吸力硬化参数;λ为塑性压缩性;Sr为有效饱和度;在式(15)中,当HIN=0 时,所对应的应力比即为临界应力比ηf;G=G(Sr)是相对于St的水分特征曲线(WRC)的导数.式(18)、式(19)分别代表失稳模式A 和失稳模式B下的临界安全系数.为了说明理论方法的正确性与适用性,下面用安全系数法针对以上算例给出相应的失稳预测如图5 所示.由图5 可知,使用安全系数法的计算结果与失稳模量法一致.特别地,由于D7试样的初始孔隙度n0小于临界孔隙度ncr,从而导致模式B 下的安全系数计算出现虚根,因此仅会发生模式A 情形下的失稳模式(滑移失稳).由以上可知,无论是从安全系数的角度还是失稳模量的角度分析,都可以较好地预测非饱和土边坡的渗流稳定性,二者能够互为验证.

图5 利用FS预测破坏模式及其相应失稳时的体积含水率与实测数据对比Fig.5 Using FS to predict the failure mode and its corresponding volume water content during instability compared with measured data
3 参数分析
为了进一步探究在不同排水条件下(恒定含水率或恒定基质吸力),模型各参数对非饱和土渗流稳定性以及相应破坏模式的影响,选取上节分析中水槽试验D4 样本并以渗流过程中失稳模量HIN的演变趋势进行说明.
3.1 初始孔隙度n的影响
上节研究表明,相对松散土更容易发生静态液化,进而引发边坡流滑失稳.因此,土体的初始孔隙度对边坡的失稳模式有较大影响.图6 为不同初始孔隙度条件下D4 样本在相同降雨条件作用下的渗流稳定性计算结果.由图6 可知,当土的初始孔隙度小于临界孔隙度(ncr=0.70)时,较难发生流动破坏[图6(a)],土体以摩擦滑移破坏模式为主[图6(b)].这是由于相对密实土在加湿过程中发生体积膨胀,产生负的孔隙水压力,不会发生静态液化.相反,当土体初始孔隙度大于临界孔隙度时,在加湿过程中发生体积收缩,产生正的孔隙水压力,因此易发生静态液化.由预测结果可知触发流滑破坏时的体积含水率要小于触发滑移破坏时的体积含水率,意味着松散土以流滑破坏形式为主.

图6 相同条件下初始孔隙度对土体渗流稳定性的影响Fig.6 The influence of the initial porosity on infiltration stability of soils under the same conditions
3.2 压缩系数λ的影响
图7为不同压缩系数条件下D4样本在相同降雨条件作用下的渗流稳定性计算结果.由于λ反映了土体的硬化规律,该值越小时屈服面随塑性应变的变化越快.因此当压缩系数越小时,失稳模量对体积含水率的敏感性越高.就破坏时的体积含水率而言,当边界条件为不排水时(恒定含水率条件),λ越大,土体体积收缩性越强,越容易在正的孔隙水压作用下发生静态液化从而发生流滑,其渗流稳定性越低[图7(a)].当边界条件为排水时(恒定基质吸力条件),由于不考虑非饱和土的变形耦合效应,λ并不影响土体的渗流稳定性[图7(b)].
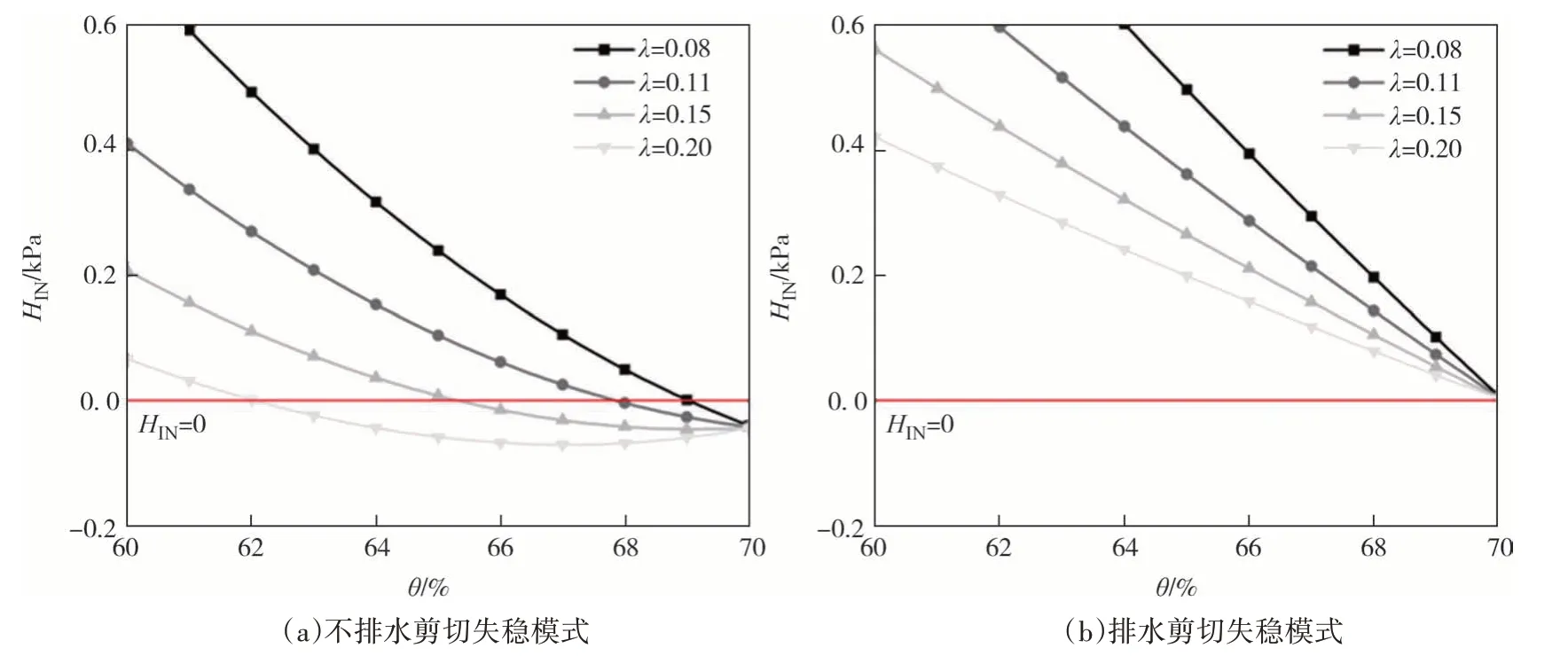
图7 相同条件下压缩系数对土体渗流稳定性的影响Fig.7 The influence of the compressibility coefficient on infiltration stability of soils under the same conditions
3.3 吸力硬化系数rw的影响
图8为不同吸力硬化系数条件下D4样本在相同降雨条件作用下的渗流稳定性计算结果.由于rw越大表明非饱和土屈服面随基质吸力的变化越大,具体表现为图中失稳模量随体积含水率变化越敏感,因此渗流稳定性越低.由于在排水加载条件下并未考虑该参数,因此rw对该条件下的不稳定模量/安全系数的计算没有影响.

图8 相同条件下吸力硬化系数对土体渗流稳定性的影响Fig.8 The influence of the suction hardening coefficient on infiltration stability of soils under the same conditions
3.4 吸力强度系数k的影响
图9为不同吸力强度系数条件下D4样本在相同降雨条件作用下的渗流稳定性计算结果.吸力强度系数k直接影响土骨架应力σ*,因此无论是恒定含水率条件还是恒定基质吸力条件,参数k的提高对土体的渗流稳定性都有着积极作用.也就是说k的增大使得土体越难发生流动破坏或滑移破坏.
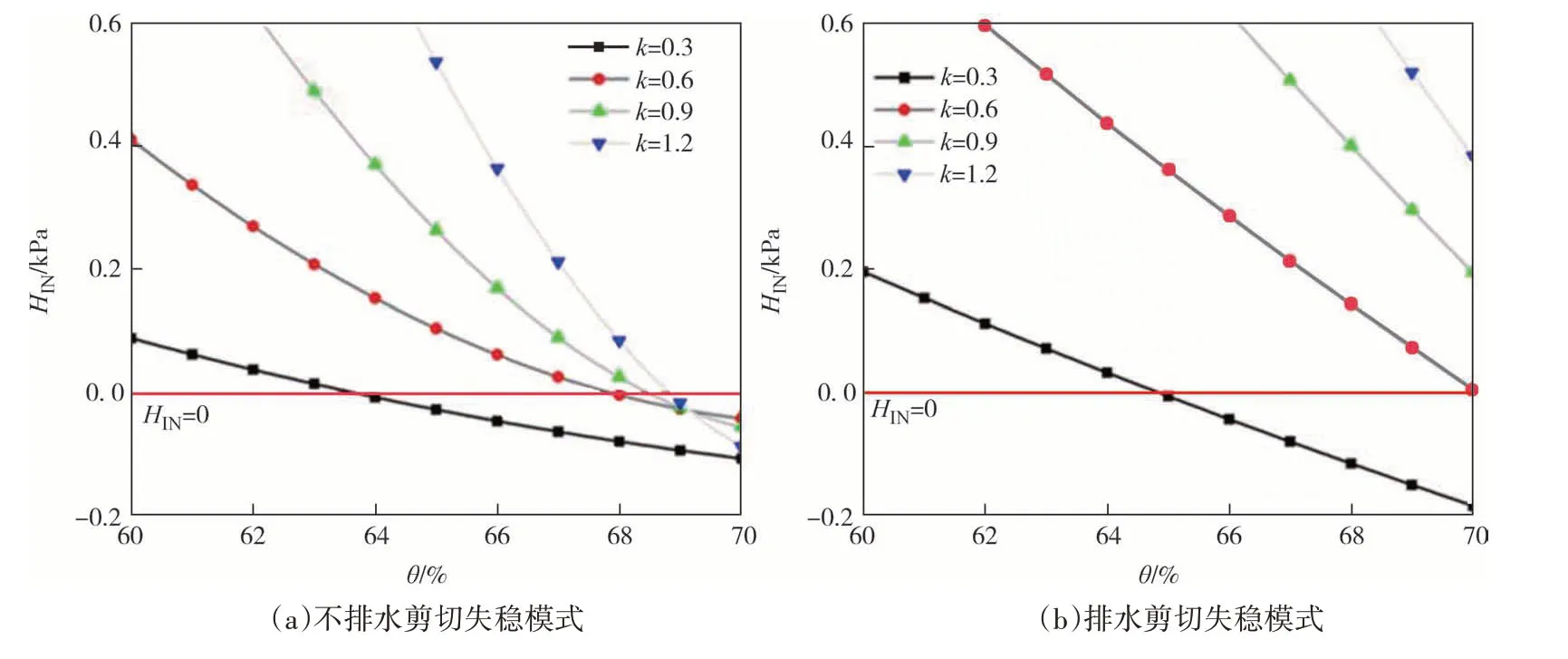
图9 相同条件下吸力强度系数对土体渗流稳定性的影响Fig.9 The influence of the suction strength coefficient on infiltration stability of soils under the same conditions
3.5 孔径分布系数α的影响
上述参数分析主要集中表现力学参数的影响,而水文模型参数同样影响着非饱和土的渗流稳定性.图10 即为Gardner 模型中不同α条件下,D4 样本在相同降雨条件作用下的渗流稳定性计算结果.由于α与土体的粒径分布有关,是与进气压力值有关的参数,因此α越大,相同体积函数率条件下基质吸力越低,非饱和土的渗流稳定性越低.

图10 相同条件下孔径分布系数对土体渗流稳定性的影响Fig.10 The influence of the aperture distribution coefficient on infiltration stability of soils under the same conditions
4 结论
1)基于失稳模量理论建立的非饱和土边坡渗流稳定性准则能较好地预测非饱和土边坡在排水条件下所发生的摩擦滑移失稳模式以及在不排水条件下发生的快速流动破坏模式(流滑).
2)初始孔隙度越大通常意味着需要更大的体积含水率才能引起土体的失稳,而相对松散土在不排水条件下易发生土体液化,进而形成边坡的流滑失稳;而相对密实土由于体积膨胀产生负的孔隙水压力,因此不易发生液化,其破坏模式以有限滑移为主.
3)压缩系数λ和吸力硬化系数rw与非饱和土的硬化特性有关.对于不排水加载条件下的流动破坏,λ(或rw)越大,土体的失稳含水率越低,即越容易发生渗流失稳.而当考虑基质吸力控制下的滑移破坏模式时,二者对土体的渗流稳定性几乎没有影响.
4)吸力强度参数k对非饱和土的渗流稳定性起着积极作用,该值越大,则触发土体失稳的体积含水率越大,即渗流稳定性越高.
5)Gardner水文模型中的孔径分布参数α对非饱和土的渗流稳定性起着消极作用,即α越大,非饱和土的渗流稳定性越低.

