考虑碾压参数影响的压实质量连续检测结果修正研究
聂志红,粟 欣,赵鹏鹏,齐 群,王学朋
(1.中南大学 土木工程学院,湖南 长沙 410075;2.中建铁路投资建设集团有限公司,北京 100070)
路基是道路工程的主体结构,良好的路基质量为道路长期承受行车荷载提供了重要保障。为使路基具有足够的承载能力、稳定性与耐久性,必须对其压实质量进行准确检测。与传统路基压实质量检测技术相比,连续压实控制技术在检测效率和检测全面性等方面的优势明显,该技术在路基工程建设中得到了广泛应用[1]。
工程实践表明,连续压实检测结果对振动频率[2]、激振力[3]、振动幅度[4-5]、行驶方向[6]、行驶速度[7]等碾压参数的变化极为敏感。为解决这一问题,保证检测的准确性,现行Q/CR 9210—2015《铁路路基填筑工程连续压实控制技术规程》[8](以下简称《规程》)对碾压参数进行了严格限制,但实际施工中为适应不同填料,达到更好的压实效果,碾压参数无法按照《规程》要求控制,这一矛盾导致连续压实控制技术难以成为压实质量的主要控制手段。为推动此技术的应用,学者们对碾压参数的影响进行了大量研究。Mooney等[7]对各碾压参数的影响规律进行了总结,并基于共振学说和轮土接触理论较为详细地阐明了其影响机理。吴龙梁等[9]采用线性回归方法分析了激振力、行进速度引起的连续压实检测数据的变化程度,聂志红等[10]、马源等[11]分别以现场试验与仿真模拟为依据,通过方差分析研究了压路机振幅、频率、速度等因素对检测数据的影响显著性。研究表明,振动方式(振动频率、激振力、振动幅度)对连续压实检测结果的影响较为显著,对行驶速度、行驶方向的影响相对较小。
以往研究[6-7,12-13]大多从压实效果来解释碾压参数对连续压实检测结果的影响机理,但相关学者[14-15]通过进一步研究发现,不同碾压参数下传统压实质量检测结果与连续压实检测结果的相关性关系并不一致。这意味着碾压参数会造成检测误差,使检测结果偏离路基的真实压实质量。因此,有必要对不同碾压参数下的检测数据进行修正,以消除误差影响[16]。吴龙梁等[17]和Meehan等[18]采用多元回归分析法,将碾压参数作为变量引入传统压实质量检测结果与连续压实检测结果的回归模型,有效提高了两者间的相关性,降低了连续压实的检测误差。但该方法存在以下局限:参数水平的确定通常依赖人为经验,极易影响多元回归分析结果的准确性;多元回归分析表达式的选择存在困难。针对多元回归分析法的不足,安再展等[19]和刘彪等[20]采用机器学习算法,基于神经网络模型分别以不同连续压实质量表征指标为目标,建立了考虑碾压参数变化的压实质量评估模型,但这类模型属于黑箱模型,其结果的可解释性较差。
综上所述,本文分别基于机器学习与多元线性回归,建立碾压参数影响下连续压实检测结果的修正模型,通过对比两种模型修正结果与传统检测结果的误差,获得最佳修正模型。进一步采用沙普利加和解释值SHAP分析各碾压参数对连续压实检测结果的影响,最后通过工程实践验证修正模型的可靠性。本研究旨在降低由碾压参数变化引起的连续压实检测结果误差,为路基压实质量的精准评价提供新方法。
1 连续检测结果修正模型
1.1 特征因子的选取
连续压实检测结果CMV具有检测原理简单、检测效率高等优点,目前已成为应用范围最广的连续压实检测指标之一。本文以CMV作为修正对象,并将其作为修正模型的特征因子之一。CMV是以振动轮竖向一次谐波的加速度幅值与基波加速度幅值的比值表征路基压实质量,计算式为[21]
( 1 )
式中:A0、A1分别为振动轮竖向基波、竖向一次谐波成分的加速度幅值,mm/s2;C为常数。
理论研究与工程实践表明,振动频率与激振力等振动参数直接影响路基压实效果,二者可以通过选择压路机挡位直接控制。然而,压路机的起振、停振、转向等均会导致振动参数产生波动,且不同挡位对连续压实检测结果的影响程度不同,因此需对振动参数进行修正。考虑同一挡位的振动频率与激振力相互对应,因此选取振动频率作为修正模型的特征因子之一。压路机行驶速度通常由驾驶者直接控制,但起步、制动、转向等操作会引起速度波动,因此行驶速度也应作为特征因子之一。此外,压路机通常以正向与反向相结合的方式进行碾压,以提高效率,然而这并不满足《规程》保持正向碾压的要求,因此,修正模型还需考虑行驶方向对连续检测结果的误差并进行修正。
动态变形模量Evd表示路基的真实压实质量,与CMV同属于动态检测,不受压路机行驶速度和行驶方向等碾压参数的影响。因此,本文选用Evd作为连续压实检测结果的修正目标值。
1.2 修正模型的建立
本文选取极限梯度提升(extreme gradient boosting,XGBoost)模型作为连续压实检测结果的修正模型,其算法原理见图1。该模型在梯度提升(GBDT)算法的基础上进行改进,在准确性、运行效率、泛化能力方面具有显著优势,可适用于复杂工况和数字化施工的大数据场景。
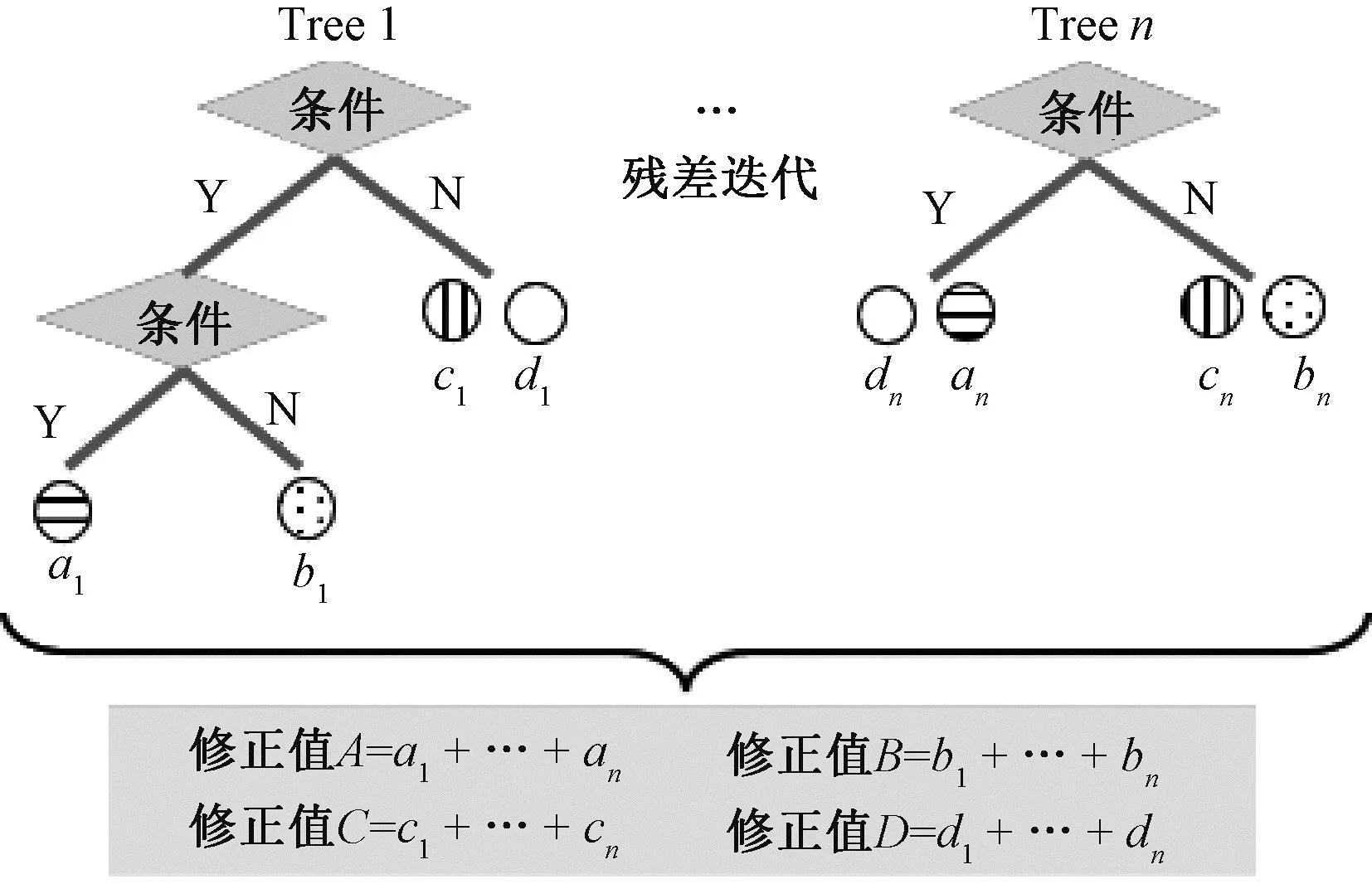
图1 XGBoost模型算法原理
基于XGBoost回归模型,本文以连续压实检测结果CMV、振动频率f、行驶速度v、行驶方向d为模型特征因子,以动态变形模量Evd为修正目标,建立了连续压实检测结果修正模型。该模型通过迭代调整,使连续压实检测的修正结果cor_CMV与目标值Evd的误差满足要求,其修正原理见图2。
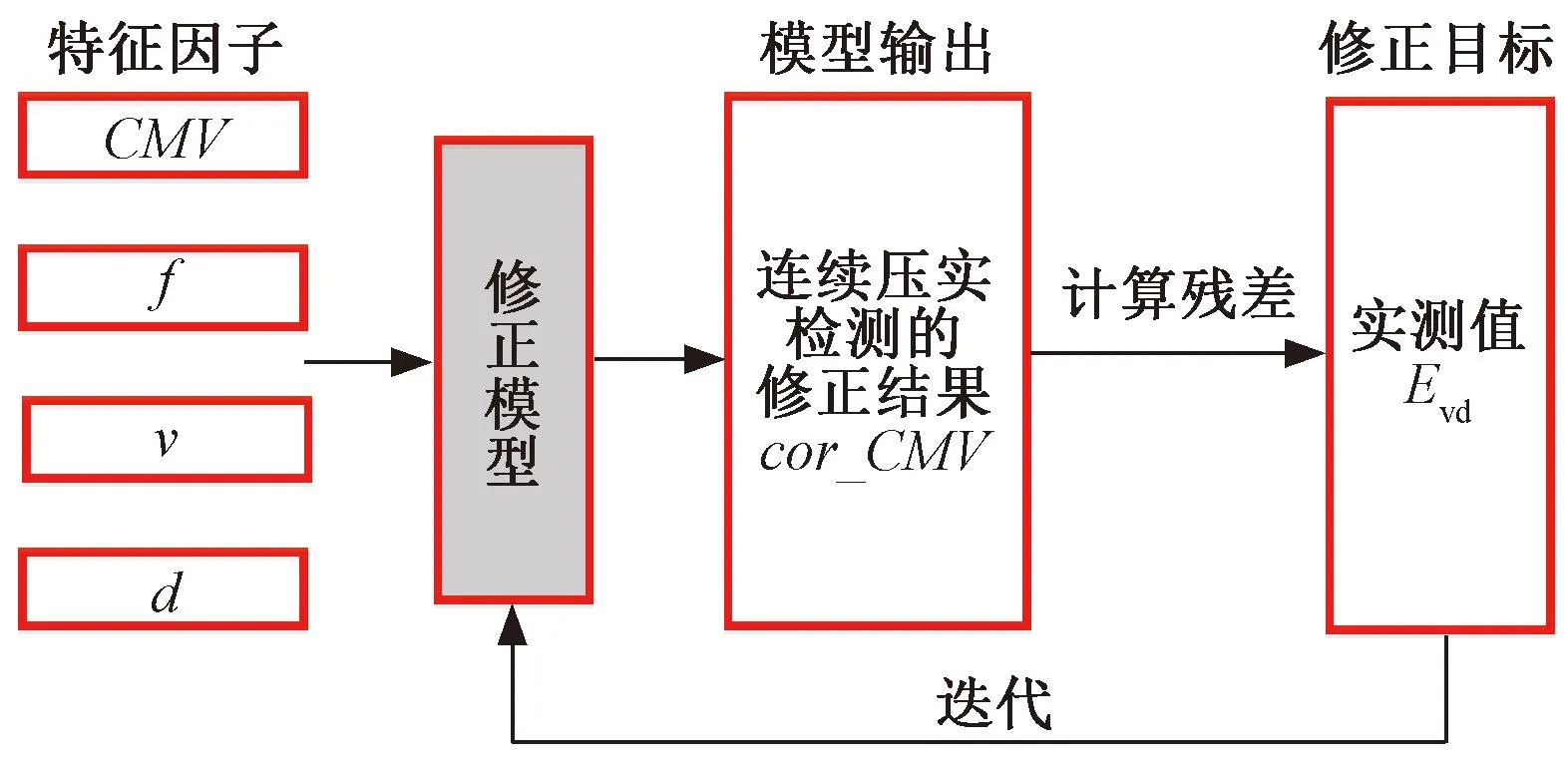
图2 模型修正原理示意
基于多元线性回归分析原理,根据式( 2 )建立实测值Evd与CMV的回归公式,从而得到修正结果CMVF的多元线性修正模型为
Evd=β1×CMV+β2×f+β3×v+β4×d+ε
( 2 )
CMVF=β1×CMV+β2×f+β3×v+β4×d
( 3 )
式中:Evd为动态变形模量;CMV为连续压实检测结果;βi为回归系数,i=1,2,3,4;f为振动频率;v为行驶速度;d为行驶方向;ε为残差;CMVF为多元线性修正结果。
2 试验概况
2.1 填料与设备
现场试验在兰张三四线铁路兰武段开展,路基填料为卵石土,填筑厚度为40 cm,现场采样获得填料的级配曲线见图3。填料的曲率系数为2.25,不均匀系数为55.69,填料级配良好。
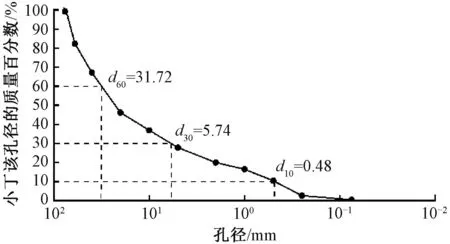
图3 填料级配曲线
碾压设备采用XG622 MH型振动压路机,工作状态下行驶速度为2.1 km/h或4.3 km/h,振动频率为28 Hz或32 Hz。压实质量连续检测设备为CCS900-CMV采集系统。该系统能实时采集连续压实检测数据CMV、测点坐标、压路机行驶速度、振动频率及振动幅度等信息,每秒输出一条数据。动态变形模量Evd采用轻型落锤仪进行检测,并通过RTK测量仪记录其测点坐标。
2.2 试验方案
试验场地大小为20 m×120 m,布置8条尺寸为2.332 m×120 m的试验带,并对每条试验段进行顺序编号。现场试验方案见表1。为模拟实际压实检测场景,提高修正模型对不同压实状态的适用性,各试验带按表1所示的预碾压工艺进行施工。压路机根据表1的设计碾压参数对各试验带进行连续检测,采集不同振动频率、行驶速度、行驶方向下的CMV,检测过程中碾压参数的波动情况如表1实测碾压参数所示。为避免叠碾对CMV检测的影响,各试验带不重叠。碾压完成后,沿试验带纵向每间隔10 m布置一个Evd采样点,每点采集3次并取平均值作为实际压实质量值。
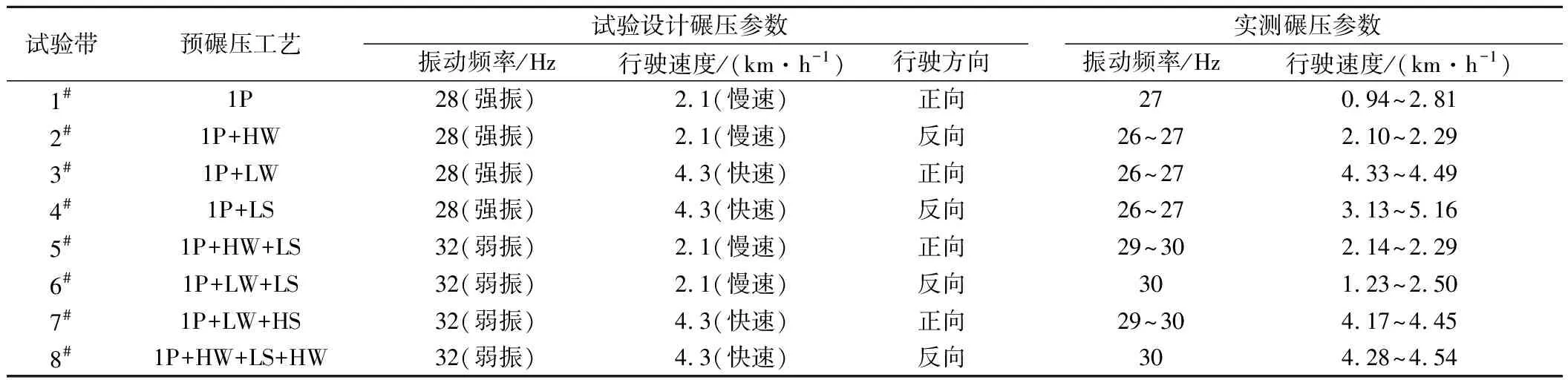
表1 现场试验方案
3 数据处理
3.1 数据集预处理与共线性检验
为提高模型训练效果,需对采集的数据进行预处理。碾压参数中,行驶方向d只存在正向、反向碾压两种情况,属于二分类变量。因此,需通过重编码将其转化为数值型变量,当正向碾压时,d取值为0,当反向碾压时,d取值为1;通过箱线图方法检测CMV、振动频率、行驶速度的异常值并将其剔除,避免影响模型结果。
本文采用方差膨胀因子VIF对各特征因子进行共线性检验,避免因共线性导致CMV修正模型出现误差或结果失真,其计算式为
( 4 )
式中:VIFj为第j个特征因子的方差膨胀因子;Rj为第j个特征因子与其他特征因子的负相关系数。
各特征因子的方差膨胀因子见表2。由表2可知,在特征因子间不存在共线性的情况下,方差膨胀因子接近1。据表2中的VIF计算结果,各特征因子的VIF值均接近1,可认为各特征因子之间基本不存在共线性,可进行后续分析。

表2 各特征因子的方差膨胀因子
3.2 Evd数据插值处理
由于现场试验中CMV与动态变形模量Evd的检测数量、范围不同,修正模型的特征因子样本与修正目标样本无法匹配。因此,采用普通克里金插值方法对试验段的Evd检测结果进行插值估计,普通克里金插值公式为[22]
( 5 )
式中:n为试验段范围内Evd的实测点个数;x0为Evd待估计点的坐标;xi、xj均为Evd实测点的坐标,i,j=1,2,…,n;Evd(x0)为坐标x0处Evd的估计值;Cov[xi,xj]为xi、xj的协方差;λi为坐标xi处Evd的克里金权重值;Evd(xi)为各实测点的Evd值;μ为拉格朗日乘子。
联立式( 5 )的第二、三项即可解得克里金权重值以及拉格朗日乘子。通过插值估计,可根据CMV测点坐标获得对应的Evd检测结果并构造数据集。将数据集划分为训练集与测试集,鉴于数据丰富的训练集可充分提高模型的训练效果。因此,本文将训练集与测试集的比例设置为8∶2。
4 数据分析与讨论
4.1 XGBoost修正模型的结果分析
XGBoost修正模型的算法通过scikit-learn机器学习包实现。由于模型的参数选取对模型修正结果具有显著影响,因此通过网格搜索结合5次交叉验证的方法(GridSearchCV)进行参数调优。
为评估模型修正结果的准确性,采用决定系数R2、均方根误差RMSE、平均绝对百分比误差MAPE共3个指标描述XGBoost修正结果cor_CMV与修正目标Evd之间的误差,即
( 6 )
( 7 )
( 8 )
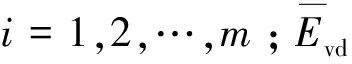
为确保数据集划分不影响模型准确性,对数据集进行了30次随机划分,不同划分情况下修正结果的R2、RMSE、MAPE波动范围均在5%内。XGBoost修正模型的评价指标结果见表3。由表3可知,在最优划分情况下,训练集和测试集中cor_CMV与Evd的R2分别为0.83与0.65,明显高于《规程》[8]要求水平(R≥0.7),表明XGBoost修正模型满足连续压实检测技术的应用要求,可适用于检测结果的修正。同时,训练集与测试集的RMSE均小于5,MAPE均小于5%,表明XGBoost修正模型具有高准确性和稳定性。

表3 XGBoost修正模型的评价指标结果
图4分别展示了测试集修正前后CMV与Evd的拟合效果。在图4(a)中,修正前的CMV与Evd呈负相关性,相关性系数为-0.379,表明在未考虑碾压参数影响情况下,CMV与实际压实质量的误差极大,不能准确评价路基压实质量。图4(b)中,修正后的cor_CMV与Evd的相关性系数高达0.808,表明考虑碾压参数影响后的CMV修正结果与实际的压实质量基本吻合,进一步验证了XGBoost修正模型在连续压实检测技术中的应用潜力。
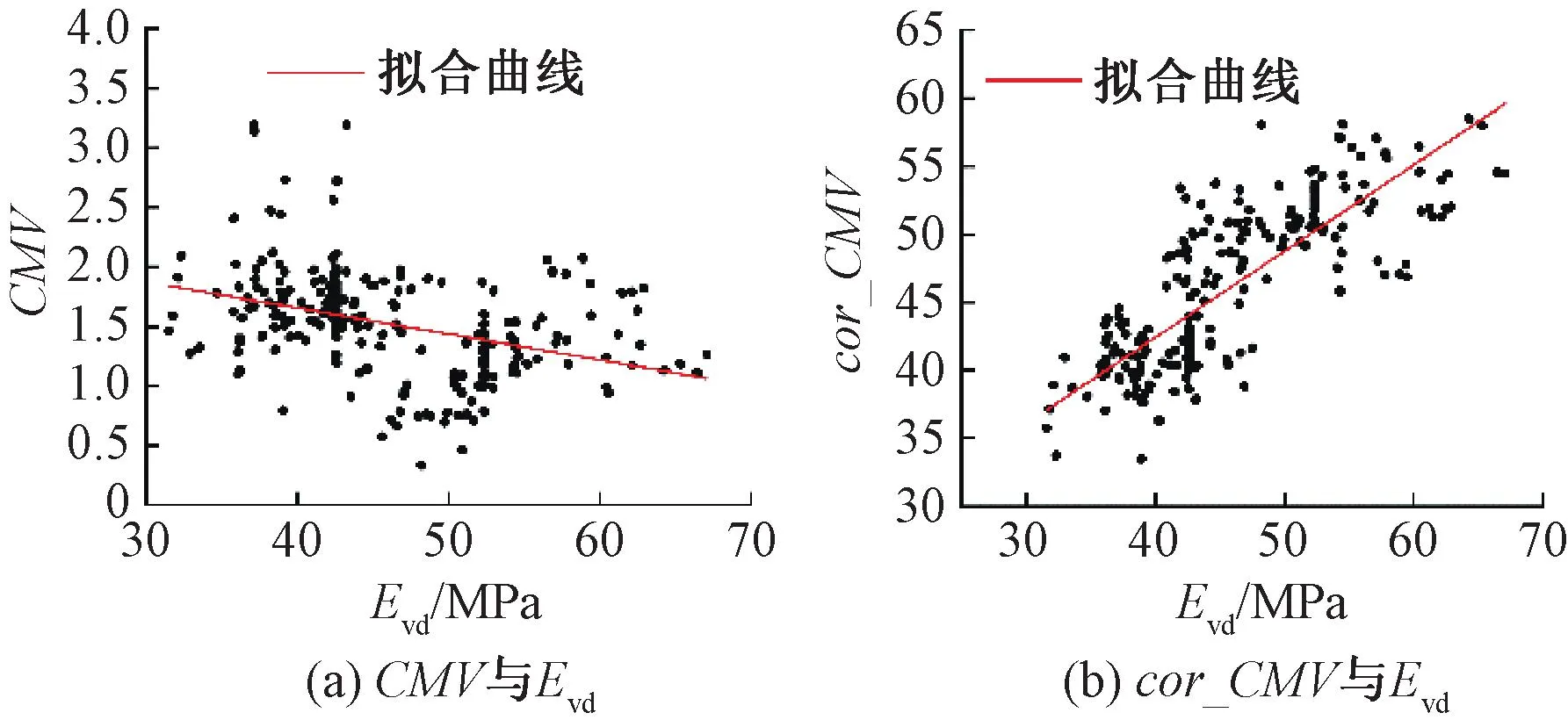
图4 测试集相关性拟合结果
4.2 多元线性修正模型的结果分析
通过训练集计算得到的多元线性修正模型为
CMVF=-3.983CMV+1.601f+11.300v+
4.587d-5.516
( 9 )
为比较该模型与XGBoost修正模型对CMV修正的适用性,同样以R2、RMSE、MAPE三种指标量化评价多元线性修正结果CMVF与Evd的偏差,其量化结果见表4,拟合结果见图5。

表4 多元线性修正模型的评价指标结果
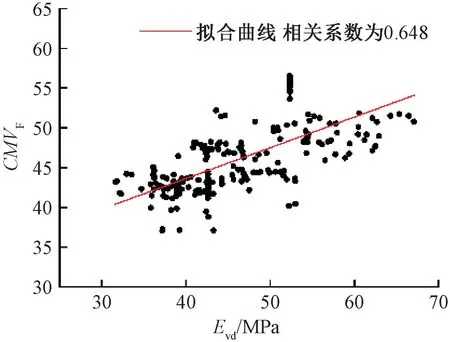
图5 测试集中CMVF与Evd的相关性拟合
相比修正前的CMV,修正结果CMVF与Evd的相关性显著提高,但仍未达到《规程》要求,不能满足连续压实检测技术的应用条件。此外,训练集与测试集中CMVF与Evd之间的RMSE均大于5且MAPE均大于5%,表明修正后的CMV与实际的压实质量检测结果仍存在较大误差,多元线性修正模型不适用于CMV修正与路基压实质量评价。这主要是因为多元线性修正模型采用线性函数进行回归,而振动频率、行驶速度等碾压参数对于连续压实检测结果的影响通常是非线性的[2,7,23-24],难以用线性函数准确表征。相比之下,XGBoost修正模型在表征变量间非线性关系方面具有强大能力,更适用于碾压参数影响下的CMV修正。
4.3 基于XGBoost修正模型的碾压参数影响分析
为分析碾压参数变化对CMV的影响程度,本文采用SHAP量化了各碾压参数对XGBoost修正模型的修正结果cor_CMV的影响。SHAP的大小能反映某个碾压参数对修正结果的影响程度,其正/负则示该碾压参数将使修正结果增大/减小。行驶速度、行驶方向和振动频率3种碾压参数对应的SHAP见图6。
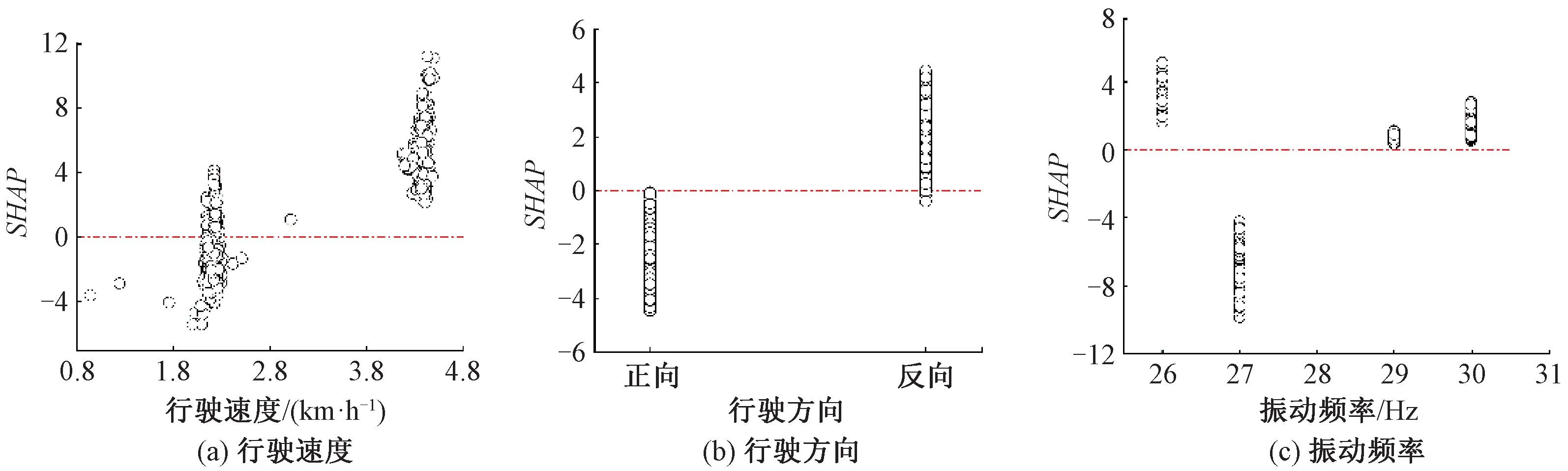
图6 不同碾压参数下的SHAP
高速行驶时(约4.3 km/h)的SHAP均大于0,表明修正结果cor_CMV在所测CMV的基础上增大。作为以Evd为目标所获得的修正结果,cor_CMV更好地代表了路基的实际压实质量。因此,高速行驶会导致CMV低于路基实际压实质量,即产生负误差。相反,低速行驶时(约2.1 km/h)的SHAP绝对值明显低于高速行驶时,表明高速行驶时的CMV检测误差更大。
正向行驶时SHAP基本为负,修正结果cor_CMV在所测CMV的基础上减小,说明正向行驶时CMV测值大于实际压实质量,即产生正误差,而反向行驶情况相反。压路机正向和反向行驶时的SHAP绝对值均在0~5 之间,表明不同行驶方向对CMV的影响程度基本相同。这主要是由于压路机的振动轮偏心块的转动方向固定,无法与压路机行驶方向同步变化,因此无论方向相同或相反,都会导致CMV检测设备所采集的加速度信号偏离真实值。
SHAP随着振动频率的增大呈现出先减后增的趋势,进一步说明了振动频率对CMV的影响是非线性的。在振动频率为26 Hz或29~30 Hz时,SHAP均大于0,表明CMV测值相比于实际压实质量偏低。振动频率为27 Hz时,SHAP为负且绝对值显著大于其他频率,表明该振动频率下CMV测值高于实际压实质量,且产生的误差相比于其他频率更显著。由于压路机的挡位限制,本文仅分析了上述振动频率对CMV误差的影响,考虑到振动频率对CMV存在复杂的非线性影响,其他振动频率下的CMV误差还需另行分析。
上述各碾压参数下SHAP绝对值的平均值,见图7,比较3种碾压参数对CMV的相对影响程度。3种碾压参数下SHAP绝对值的平均值相差不大,表明3种碾压参数对CMV均存在显著影响且各碾压参数造成的CMV误差接近。由此可见,在压实质量连续检测技术的应用过程中必须考虑碾压参数造成的检测误差并对CMV进行修正。
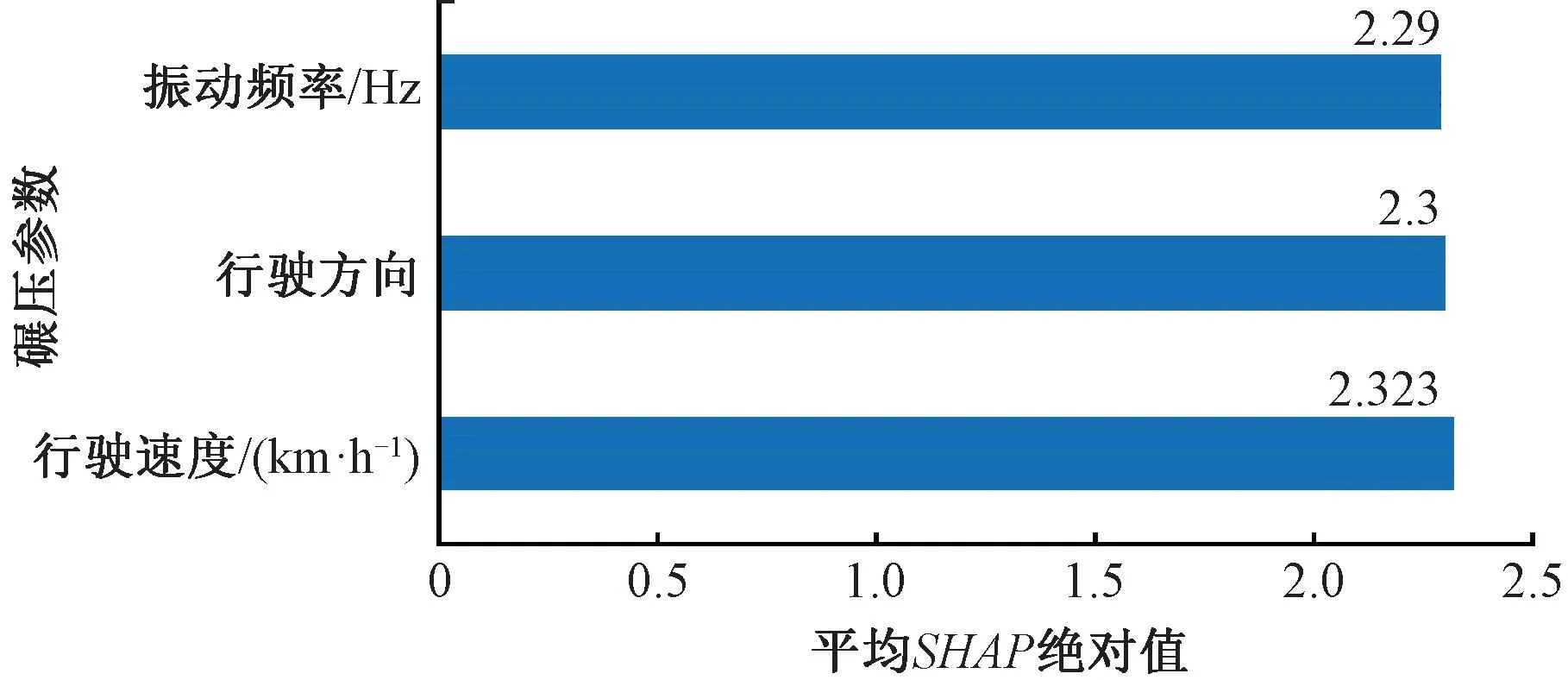
图7 各碾压参数下SHAP绝对值的平均值
5 工程应用与验证
在试验场地所在标段内选取了另一段具有相同填料类型、摊铺厚度和碾压工艺的路基,并对该路基段进行CMV与Evd检测,其中Evd检测的采样间距为10 m。检测完成后,利用XGBoost修正模型对CMV进行修正,并分别对修正前CMV、修正结果cor_CMV和Evd进行克里金插值,获得三种指标的空间可视化效果,见图8。最后,通过三种指标空间可视化效果的对比,实现对XGBoost修正模型的可靠性验证。

图8 三种压实质量评价指标的空间可视化
由图8可知,相比于修正前CMV检测结果,cor_CMV显然与Evd更为吻合,表明XGBoost修正模型较好地降低了由碾压参数引起的检测误差,使结果更贴近路基的实际压实质量,提高了连续压实检测技术的可靠性。此外,从图中绿色标注的压实薄弱区域来看,尽管cor_CMV与Evd的检测结果基本对应,但二者之间存在一定的范围差异,这主要因为Evd的采样间距较大。这一现象表明,相较于Evd等传统检测方法,修正后的检测结果cor_CMV更有助于精准定位路基的压实薄弱区域。总体而言,XGBoost修正模型保持了压实质量连续检测技术在检测效率与检测范围等方面的优势,同时显著提高了检测结果的准确性,因此在路基压实质量评价领域具有较高应用价值。
6 结论
本文依托兰张铁路工程开展现场压实试验研究,通过建立XGBoost修正模型、多元线性修正模型,分析了压路机碾压参数对连续压实检测结果的误差影响,并对比了修正模型的适用性。本文主要得到以下结论。
1)XGBoost修正模型的修正结果cor_CMV与压实质量实测值Evd较为接近,该模型有效地降低了碾压参数造成的检测误差。此外,XGBoost修正模型的可靠性通过工程实际得到了进一步验证。
2)基于多元线性回归方法的修正模型虽然在一定程度上提高了CMV修正结果与Evd的相关性,但该模型的修正误差远高于XGBoost修正模型。由于多元线性修正模型难以表征碾压参数的非线性影响,修正后的结果仍不满足相关规程要求,该模型不适用于碾压参数影响下的CMV修正。
3)碾压参数对CMV影响的量化分析表明,高速行驶对CMV影响极大且导致检测结果偏低,不同行驶方向对CMV的影响程度相当但误差相反,振动频率则对CMV产生非线性影响且误差与振动频率取值有关。上述碾压参数对CMV的影响程度显著且接近,进一步证明了CMV修正的必要性。
4)受试验条件限制,本文主要研究了单一工况下碾压参数对CMV的误差修正方法,但实际施工中XGBoost修正模型的适用性可能受路基填料的种类与含水率、下卧层的压实质量、填筑厚度等因素的变化影响,有待后续研究对此进行优化。

