基于耗散能的高速铁路路基填料动力安定临界阈值研究
毕宗琦,叶阳升,蔡德钩,闫宏业,张先军,尧俊凯,苏 珂
(1.中国铁道科学研究院集团有限公司 铁道建筑研究所,北京 100081;2.中国铁道科学研究院集团有限公司 高速铁路轨道系统全国重点实验室,北京 100081;3.中国国家铁路集团有限公司,北京 100844;4.中国国家铁路集团有限公司 工程管理中心,北京 100844)
路基填料作为构成基床结构的基础原材料,其在行车振动作用下的力学特性与变形演化规律与路基结构整体耐久稳定性存在直接的关联。如何合理地分析评估并保障路基填料的长期工作性能,进而控制路基不均匀变形,确保其全寿命周期内的服役性能,是高速铁路(以下简称“高铁”)建设运营中需要考虑的关键问题之一。
近年来,国内外学者在针对高铁路基填料动力学特征与长期变形相关研究中,主要获取其填料在不同因素影响下循环加卸载塑性应变的累积发展规律,包括应力水平[1-2]、循环作用次数与频率[3-5]、密实度[6-7]、应力历史[8-9]、细粒含量与含水率[10]等,并针对其不同发展模式与收敛性特征展开讨论。Heath等[11]、蔡英等[12]根据累积塑性应变与荷载作用次数的关系曲线,通过在半对数坐标下曲线的凹凸性进行判别,将其分为发展和衰减两种类型。王龙等[13]将累积塑性变形曲线分为稳定型、衰减型和破坏型,并分别给出了不同状态间的临界累积应变量。Minassian[14]以体积塑性应变为判断依据同样将循环荷载作用下的累积塑性应变分为三个状态。焦贵德等[15]结合土体临界动应力的概念,将累积应变特征分为稳定型、破坏型和临界型三类。聂如松等[16]同样给出了此三类累积应变形态,并根据累积应变斜率和循环振次线性关系,提出了以围压、含水率、静强度为变量的临界动应力经验公式。文献[17-18]基于循环荷载作用下基床填料累积变形演化状态特征,提出了快速稳定、缓慢稳定、缓慢破坏和快速破坏4种类型,建立了基于累积变形速率发展趋势的幂次判别法,探讨了铁路路基基床结构变形状态的控制原则和技术条件。文献[19-20]基于临界状态土力学基本原理,以控制重复荷载下填料不发生变形和孔压累积的角度提出了基于临界体积效应应变的高铁路基基床结构分析与应变控制设计方法。
在高铁百年的使用服役期内,路基填料经受的列车动载循环次数可达数亿次,面临着高周次加载长期作用(循环次数N>105)和复杂多维度荷载组合两方面的问题。在设计实践中,为了保证铁路路基的长期使用性能,路基填料需要满足在外界复杂荷载作用下长期保持稳定,使运营期不发生变形的累积。在上述背景下,考虑到试验与模拟成本、计算冗余误差以及相应参数获取等困难,通常意义下面向低周次荷载的分析评估理论方法往往很难直接对高周次行车振动作用下高铁路基填料的长期变形发展模式以及耐久稳定状态进行有效地分析评估。
作为一种有别于常规弹塑性增量分析的临界状态方法,安定理论方法为预测结构的安全性、评估长期变形趋势和稳定性提供了有效的分析途径。其最早是由Melan等[21]提出,并由Maier[22]、Ceradini[23]和Polizzotto[24]进一步发展。安定理论从结构抵抗并适应外部复杂荷载作用从而保持长期稳定能力的角度给出了分析评价准则。与传统方法相比,安定性分析不需要精确的荷载历史和时间历程,通过安定性分析,可区分不同的变形累积趋势线,获取稳定的临界条件,并据此确定材料的安定性质。近年来,安定理论在岩土工程中的应用越来越广泛,如路面车辙变形[25]、海洋平台地基承载能力[26]、边坡稳定性[27]以及无砟轨道结构[28]的相关评估和分析中。安定荷载已逐渐成为工程强度设计规范中塑性失效准则的重要理论判断依据,为面临长期动载下的高速铁路路基劣化评估、临界荷载的选取、长期变形的预测与控制等提供了有力的分析工具。
近年来,国内外学者借助安定理论方法,针对岩土体类材料的永久变形发展趋势以及安定临界阈值开展了一系列研究,提出了不同的安定状态分类依据和临界安定状态判定标准。Werkmeister等[29]将轴向累积塑性应变变化值作为动力行为类型的划分依据,利用加载曲线中代表性阶段应变速率对变形趋势和三类安定状态进行判别,并给出了基于永久应变差值的安定临界条件经验值。Chen等[30]在此基础上,基于塑性应变-加载次数半对数曲线中的次循环压缩阶段的斜率作为安定状态划分依据。Xiao等[31]则利用累积应变、应变速率、回弹模量等曲线作为判断安定类型的依据。Xiao等[32]针对铁路道砟材料,依据累积塑性应变及塑性应变率曲线变化规律给出了安定状态、塑性蠕变状态和增量破坏状态三种类型的判别。郑可扬等[33]针对不同动态应力路径下粗粒土路基填料轴向累积塑性应变发展规律,考虑循环围压效应,提出了基于Savitzky-Golay 滤波法的永久变形行为不同阶段划分方法。徐方等[34]建立了分析累积应变曲线类型与围压、动应力等相关性的灰色关联模型,以及预测临界动应力的BP神经网络模型,提出了考虑围压和含水量影响效应的粗粒土临界动应力经验公式。上述方法针对不同种类岩土体材料获取了大量有价值的结论,但安定临界判据的选取大多来源于对试验累积变形数据和应变率曲线形态、斜率等的表观规律分析和相关性分析,对不同变形发展趋势以及安定临界状态之间的理论关联还有待进一步研究。
本文在现有安定状态划分与临界值判别依据的基础上,从能量的角度入手,研究揭示行车振动循环动力作用下路基粗粒土填料的塑形应变累积特性、循环应力-应变滞回特性以及耗散能演化规律,建立长期变形趋势、安定临界状态与耗散能间的映射关系,提出基于等效单位体积耗散能的安定临界状态判别标准和相应控制阈值确定方法。研究成果可为高铁路基填料安定性分析与长期服役性能评估提供理论支撑。
1 典型高铁路基粗粒土填料动三轴试验
1.1 大直径三轴试验系统
本文采用大直径三轴试验系统开展研究,试验系统主要包括动力加载系统、压力室、围压控制系统、数据采集与控制操作系统等部分。其中,动力加载系统由伺服电机闭合回路控制,轴向力为0~64 kN,频率为0~5 Hz,位移行程为±100 mm,控制精度为0.20 μm。可提供高精度的动态荷载控制性能,压力室适配最大直径为300 mm的三轴试样,满足粗粒土试样配置尺寸要求。试验系统的组成示意见图1。
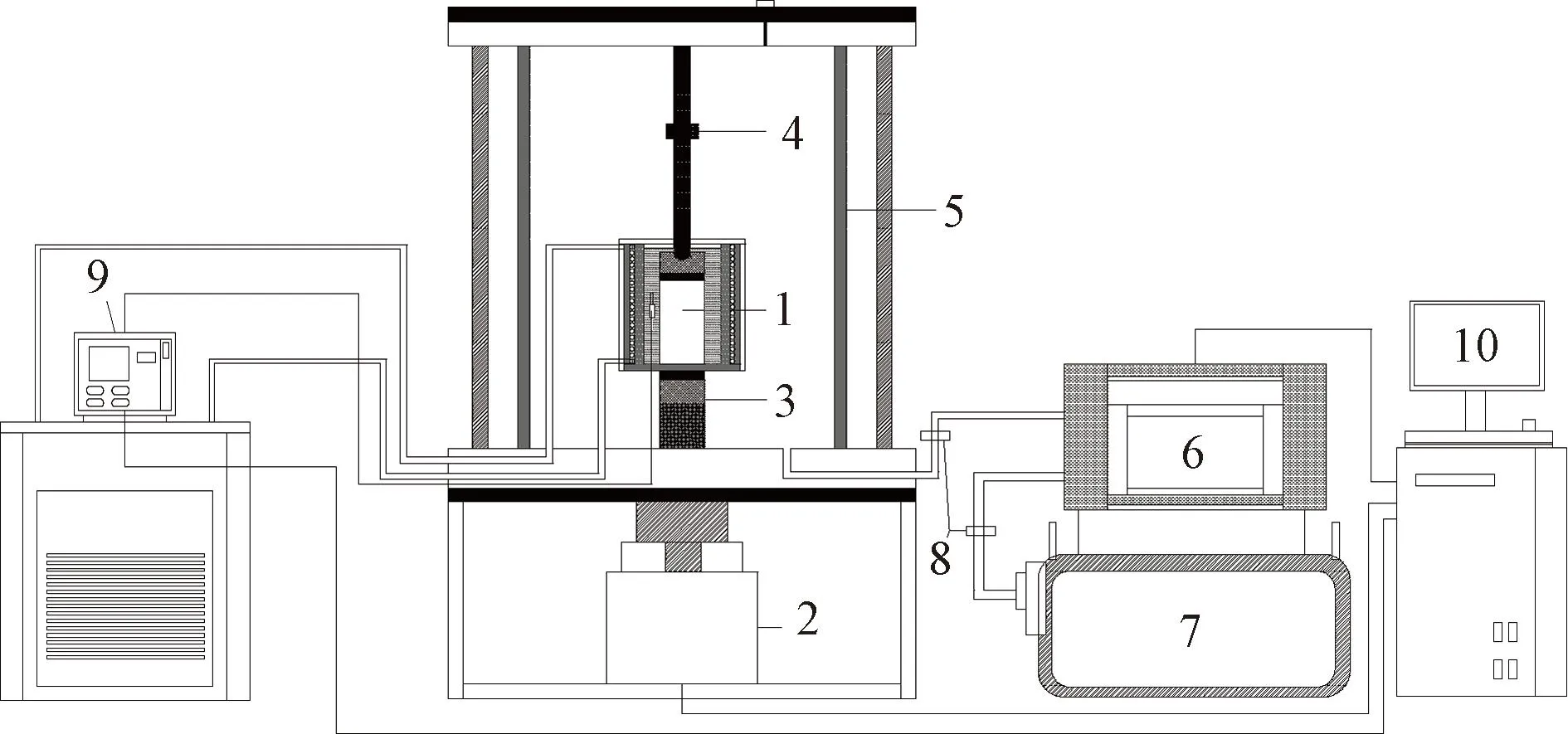
图1 试验系统组成示意
1.2 试验材料与试样制备
试验所用三轴试样参照我国高速铁路路基典型粗粒土填料级配进行制备。根据筛分试验将其分为8组不同粒径的颗粒组分,典型组分见图2。试验采用的三轴试样直径为150 mm,高度为300 mm。根据最大颗粒粒径不宜大于试样直径的1/6~1/5的要求,试验采用等量替代法对取土原样进行颗粒级配调整,最大颗粒直径定为20 mm。调整后级配曲线见图3,试样不均匀系数Cu、曲率系数Cc分别为110.8、24.1,根据TB 10001—2016《铁路路基设计规范》[35],属B组填料。经前期击实试验测试,试样最大干密度和最优含水率分别为2.44×103kg/m3和5.1%,结合TB 10001—2016《铁路路基设计规范》基床压实标准[35],试样按最优含水率5.1%配置,压实度按0.97控制。

图2 三轴试样典型粒径颗粒组分示意(单位:mm)
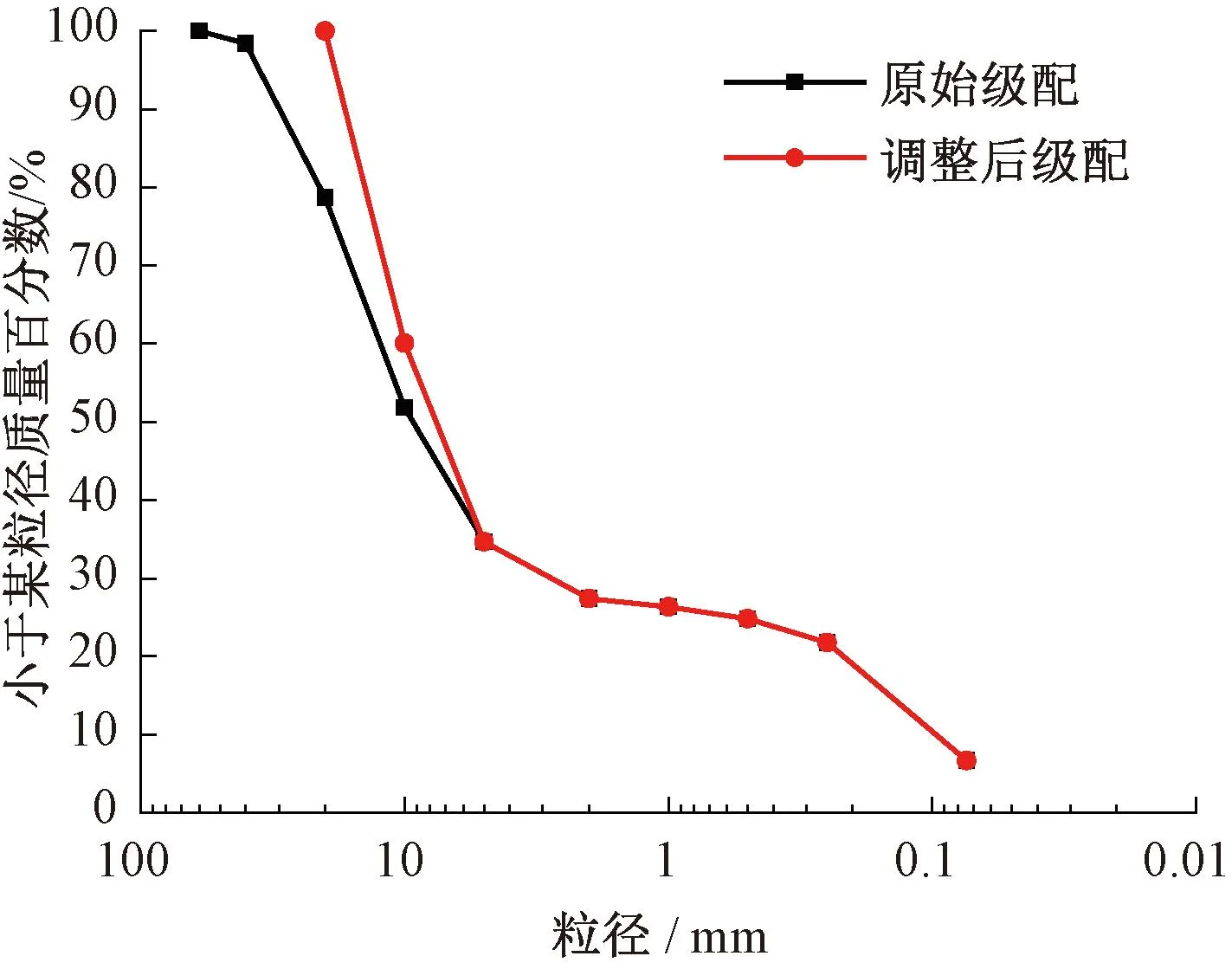
图3 路基填料颗粒级配曲线
1.3 试验方案与流程
1)初始设置
施加动载前首先施加初始围压条件,以模拟钢轨、轨道板等上部结构静载作用下,填料在路基基床所处不同深度位置的初始应力状态。依据TB 10001—2016《铁路路基结构设计规范》路基结构的分层厚度[35],分别取基床底层表面、基床底层中心以及基床底层底部位置开展研究,与3种位置相对应的试验围压设置为15、30、60 kPa。
2)动载施加
针对填料试样开展长期循环加载利用作动器在试样轴向施加不同幅值的循环动载以模拟列车动力作用的影响。由于实际高速列车通过路基断面是一个短暂过程,因此采用不排水动三轴试验。为保证加载过程中初始阶段不产生不规则冲击力,同时确保加载曲线稳定,需施加初期轴向压力,经过尝试设置为0.01 kN,其值远小于静强度,对试验结果影响较小。
在荷载水平和加载方式方面,通常高铁无砟轨道路基所受的动应力幅值大致为17~23 kPa,有砟轨道则大致为80~100 kPa[36-39]。本研究主要目的是通过一系列动应力幅值下的试验,以获取填料不同应变发展趋势间的临界状态。因此试验中动应力幅值的取值并非严格按照实际高铁路基所受动应力幅值,而是由小至大逐级递增,模拟试样由稳定状态发展至最终发生破坏,荷载最大值往往超出高铁路基动应力常规水平。试验中采用单级加载形式与分级加载两种形式,考虑高周次循环作用影响,试样设定总加载次数均大于105。其中单级加载试验首先施加初始固结应力σ3,随后施加幅值为σd的循环动应力,针对一个试样动荷载幅值固定不变,循环总次数N=105次或累积变形达5%时试验终止。分级加载试验则针对一个试样施加幅值由小至大的若干级动载,第一级荷载幅值ld,1=0.4 kN,后续每级幅值增量Δld= 0.2 kN,换算每级动应力幅值递增量约10 kPa,每级荷载循环次数ΔN=104次。本文主要采取简化复杂的频谱成分的方法,试验荷载模拟列车荷载时认为其动荷载是由相邻两节车厢2个转向架对路基作用为一个加载循环[40-41],列车速度为400 km/h时对应频率约为4.5 Hz,结合实际加载设备条件和工作情况,取加载频率为5 Hz,最高可对应模拟列车运行速度为450 km/h下通过时相邻转向架引起的荷载频率。
三轴试验方案与控制条件见表1。本文主要关注围压水平σ3、动应力水平σd、加载次数N的影响。由表1可知,试验按照2种加载方式分为2个组别,G1组为单级加载形式,考虑围压大小的不同,分析不同动应力幅值下的应变累积规律,主要目的是获取长时间尺度下填料的塑性变形累积和塑性应变率变化的完整曲线,分析长期变形发展的基本规律。G2组为分级加载形式,主要目的是利用递增荷载寻找试样由稳定转变为不稳定状态的临界条件与对应控制阈值。

表1 三轴试验方案与控制条件
2 填料长期变形演化与能量耗散规律
2.1 长期变形发展趋势与塑性应变率演化规律
基于连续加载下的试验结果,获取了路基填料在不同循环应力水平下的永久应变发展曲线。以高铁路基结构基床底层表面、基床底层中心以及基床底层底部位置的典型围压环境所对应的试验工况为例,不同动应力幅值下试样累积变形、应变率的变化曲线分别见图4、图5。
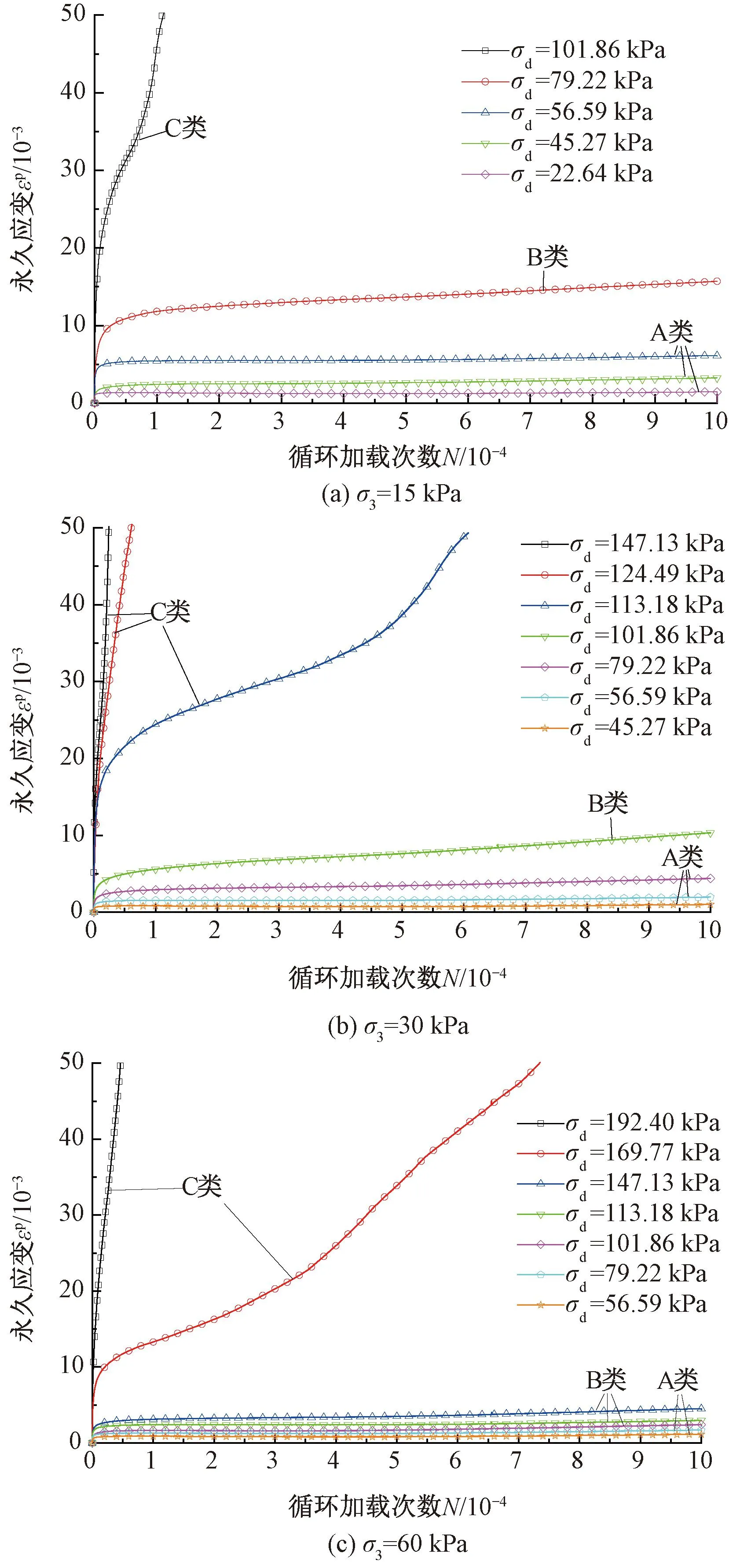
图4 不同动应力幅值下试样累积变形曲线
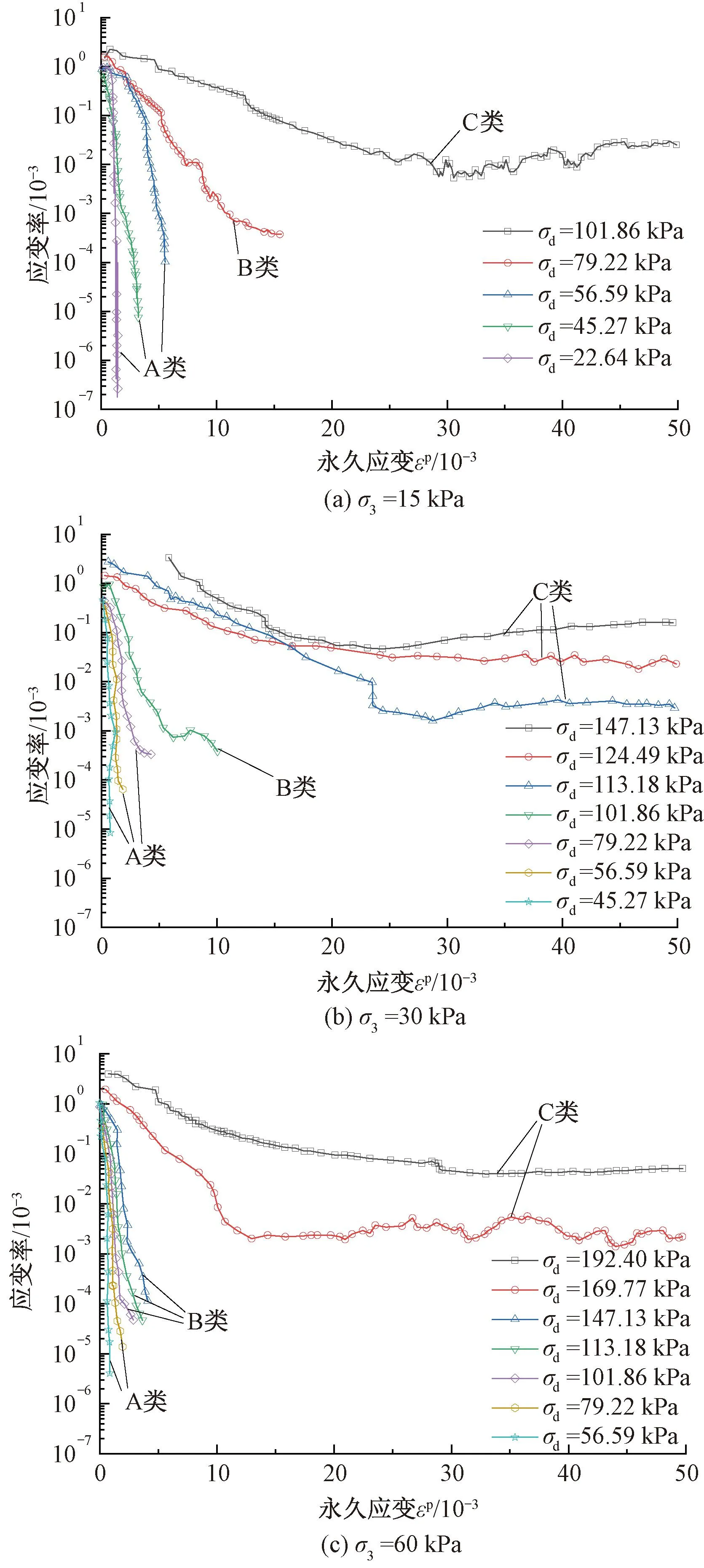
图5 不同动应力幅值下试样应变率随永久应变的变化曲线
由图4可见,不同的动应力幅值下,填料的永久应变随加载次数的累积规律存在明显的差异。当动应力幅值足够小时,累积曲线除起始若干个循环产生少量的应变累积后,后续长时间都处于稳定状态,变形不再发生新的累积,即图中的A类;随着动应力幅值的逐步提高,应变的发展速率逐渐增大,在此过程中每一个外载循环内都会产生新的变形累积,永久变形呈现出持续缓慢增长的整体趋势,即图中的B类;若动应力幅值超过一定界限,永久变形将难以维持稳定状态,在很短的时间内发生大变形累积(超出5%变形量),试样发生破坏,永久变形的曲线呈现出快速上升的趋势,即图中的C类。根据累积应变的发展趋势,即使在小应力水平下,所有试验结果也都表现出一定的永久应变,这说明在列车行驶荷载作用下铁路路基填料并不会处于纯弹性状态,不论荷载作用大小,路基填料总是会表现出一定的永久或回弹变形特性。
与永久应变相对应的,应变的累积速率可以进一步体现出上述三类应变累计发展趋势和不同稳定状态的填料变形演化规律。依据同组试验下的应变速率分析结果,计算获取了不同动应力幅值下应变累积速率与循环次数的关系。由图5可见,不同动应力幅值下试样的应变累积速率同样分为A、B、C三类。以围压σ3=30 kPa的结果为例,其中A类试样应变累积速率随永久变形量的增加快速下降,迅速达到1×10-5/cycle以下,不产生变形的持续累积;B类试样应变累积速率随永久变形量的增加缓慢下降但曲线有一定的偏转,最终停留在1×10-3~1×10-4/cycle之间,试样的变形仍在持续发展;C类试样应变累积速率随永久变形量的增加存在少量的下降,但最终维持在一个较高的水平,约在0.1~0.01/cycle,且随永久变形的持续增加,可能速率会出现反向增大的现象,最终超出5%最大应变,认为达到破坏状态。
2.2 循环加载条件下滞回曲线与能量耗散特征
岩土体在承受循环荷载过程中,其内部发生着能量的存贮,也伴随着能量的消耗。能量耗散是岩石变形破坏的本质属性,反映了材料本征强度不断弱化并最终丧失的过程[42]。循环荷载下滞回圈与能量耗散的关系见图6,滞回圈的试验现象也是能量变化的表现形式。
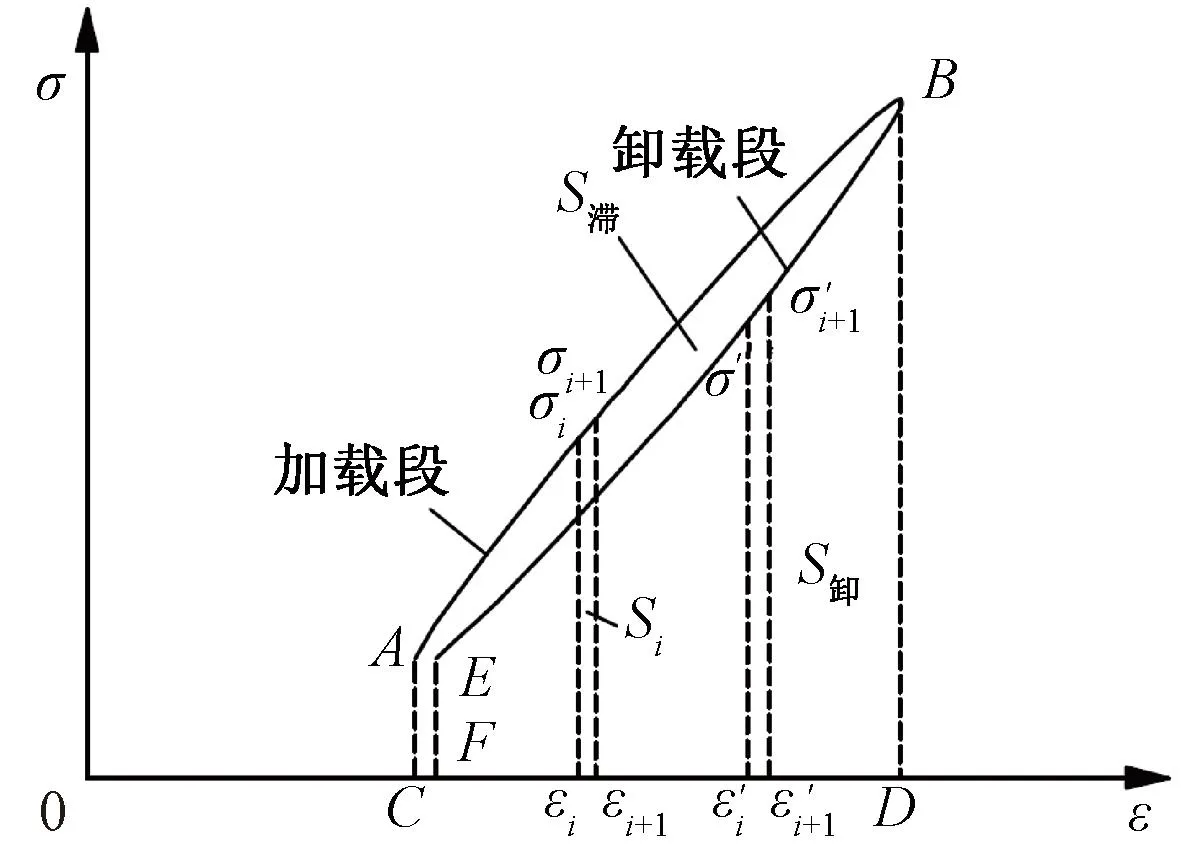
图6 循环荷载下滞回圈与能量耗散的关系
由图6可见,在应力-应变滞回圈中,加载段与横轴所包围的面积为单位体积能,表示外力对试样所做的功;卸载段与横轴所围面积S卸为单位体积弹性能;加卸载曲线面积差为单位体积耗散能,也即滞回圈面积S滞。其值越大代表该耗散的能量越多,相对的试样更趋向于发生材料损伤和不稳定破坏。基于积分累积方法,单位体积耗散能Ud可表示为
( 1 )
式中:U为总的单位体积能,Ue为单位体积弹性能;σ、ε分别为加载段应力、应变;σ′、ε′分别为卸载段应力、应变;σi、εi分别为拆分后第i段应力、应变。
列车长期循环动载作用下,A、B、C三类长期变形发展趋势对应的不同加载循环内滞回曲线见图7。以30 kPa围压下的试验结果为例进行讨论。为展示不同变形发展阶段的应力-应变演化特征,分别提取加载次数为N=100、1 000、10 000、100 000下的滞回圈进行对比分析,对应于加载起始阶段、初期发展阶段、中期发展阶段和结束阶段。由于C类累积变形发展较为迅速,很快即达到破坏状态,故最终的加载次数与破坏时间相关,并非100 000次。
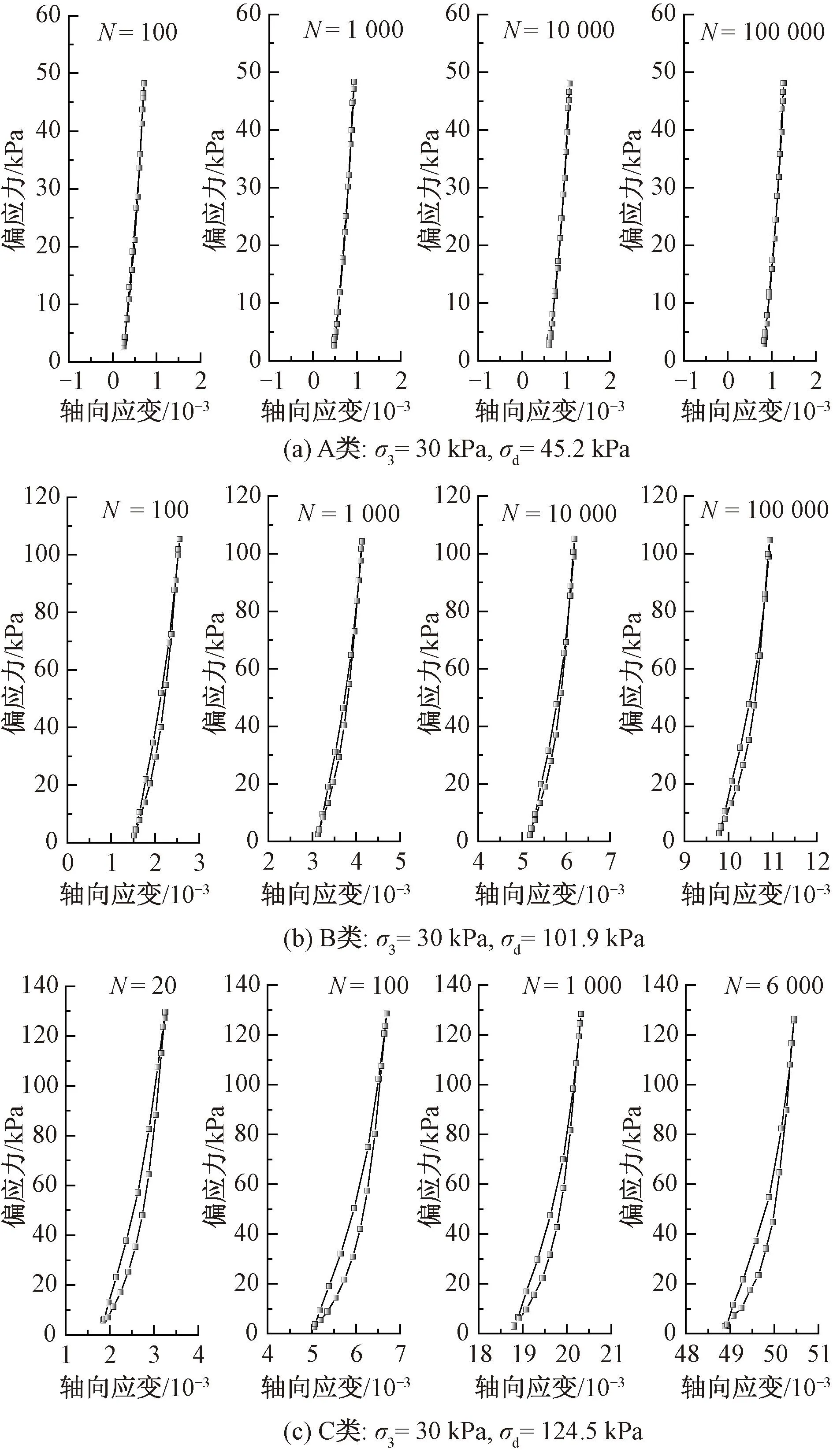
图7 不同加载循环对应滞回曲线
滞回圈形态以及能量耗散特征与填料在循环加载下的长期变形发展模式与稳定状态之间存在密切关联。由图7可见,对于A类,各阶段滞回圈形态均近似为线性,应力-应变关系呈现弹性响应,即每一个循环内几乎没有新的塑性耗散功产生,试样不发生变形累积;对于B类,滞回圈的形态呈现较细的月牙状,滞回圈面积较小,每一个循环内均产生了一定的塑性耗散功,但滞回圈的形态随加载阶段发展整体变化不大,说明变形的累积增量速率趋于一个较为稳定的常量;对于C类,变形发展的各阶段滞回圈的形态呈现较宽的月牙状,应力-应变关系呈现强烈非线性,滞回圈面积较大,试样的变形持续快速累积。
试样单位体积耗散能随加载次数的变化规律见图8。由图8可见,A类单位体积耗散能Ud始终处于约0~0.005 kJ/m3的较低水平,且较为稳定;B类单位体积耗散能Ud处于约0.005~0.015 kJ/m3的范围,在一定循环次数后呈现轻微上升趋势,上升幅度不超过0.005 kJ/m3;C类单位体积耗散能Ud通常大于0.02 kJ/m3,且波动较明显,随加载次数的增加上升显著,最终破坏时可达0.05 kJ/m3左右。
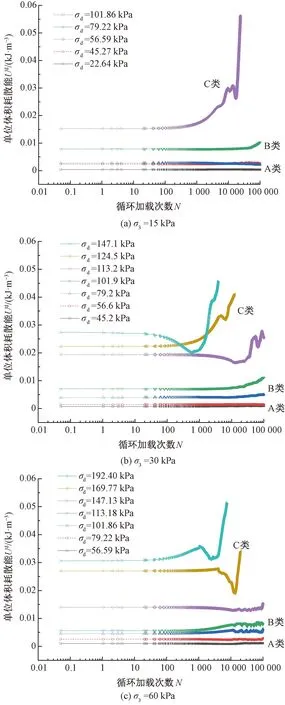
图8 试样单位体积耗散能随加载次数的变化规律
2.3 不同加载模式下长期变形与能量耗散规律对比
为快速高效获取不同发展模式之间的临界条件,开展多级加载试验进行分析。以30 kPa围压下的试验结果为例,永久应变随循环加载次数变化的累积发展曲线见图9。图9中,i为加载阶段数。由图9可见,试样的永久变形随每级外部动载幅值的增大而逐渐出现变形的累积,且累积发展速率逐级增加。初始的若干级荷载下永久变形尚能看出较为显著的稳定收敛趋势,至后续临近破坏阶段则呈现持续向上发展的非稳定状态。
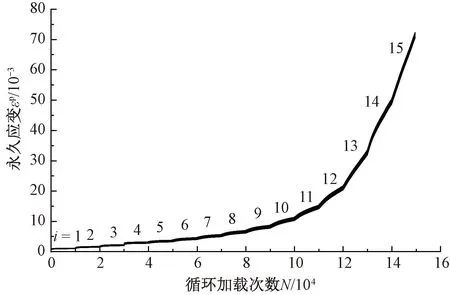
图9 多级加载条件下永久变形随加载次数累积发展曲线(σ3=30 kPa)
多级加载条件下应变累积速率随永久变形量变化曲线见图10。由图10可见,多级加载条件下的应变率曲线同样可以按A、B、C三种模式进行区分,与单级加载在应变率发展收敛性规律、变化量值方面较为近似,随动应力幅值的增大,多级加载的应变率呈现出:A类型快速衰减至1×10-5/cycle以下;B类型衰减至1×10-5~1×10-3/cycle并呈现一定的倾斜趋势;C类型则较快速稳定在1×10-3~1×10-2/cycle。
多级加载条件下试样单位体积耗散能的变化规律见图11。由图11可见,A、B、C三类变形模式下单位体积耗散能随加载次数的变化曲线与单级加载条件下试验结果类似,A类的单位体积耗散能为0~0.005 kJ/m3的较低水平,B类单位体积耗散能为0.005~0.015 kJ/m3,C类单位体积耗散则大于0.02 kJ/m3,三种类别在量值和发展趋势上均与单级加载条件相近。
综上,相较于单级加载方式,多级加载中试样受到前序低动应力幅值时的循环加载,虽然可能会产生一定的压密作用,对填料的累积塑性应变随振次的变化产生影响,主要体现在后续加载级的单阶段累积应变增量会相较同样条件下的单级加载方式要略小。对比图5和图10,单级、多级加载的塑性应变率变化曲线主要体现在两者曲线的起始点不同,以及弯曲下降的形态有所区别。主要原因是分级加载延续上一级的永久应变继续累积,因此横坐标起始点会右移,同时由于试验材料、应力历史等多方面影响,具体的曲线形态有一定差别,但从应变速率随应变量发展是否收敛以及最终的稳定值上看两者规律基本一致,从判别安定临界条件并划分三类变形发展趋势的角度来看,其影响较小。基于上述对比分析,单、多级加载的数据规律均可以反映三类不同的长期变形演化规律。鉴于多级加载试验中的动应力幅值增量可控,加载耗时和试验成本均远小于单级加载,采用多级加载数据进行长期变形发展模式判别是合理可行的。
3 填料变形模式与安定特性的关联
在安定理论体系中,当一个具有弹塑性的结构或系统受到一循环荷载作用时,根据应力-应变水平的差异将出现不同的变形发展状态和收敛性趋势,呈现不同的安定特性。材料应力-应变关系表现的安定特性如图12所示,A类区域的累积应变在初始的几个周期即达到稳定,后续不发生新的变形累积,为“塑性安定状态”;B类区域的累积应变始终缓慢的增长,表现出持续累积发展的“塑性蠕变状态”状态;C类区域的累积应变则在较短的时间内发生了突增,为“增量破坏状态”。与之对应的,应变率同样按照此规律划分为三类不同的发展趋势。
由前述试验结果可知(图4、图5、图8),累积应变曲线、应变率、单位体积耗散能的变化均与所受动应力、动应变水平有关,呈现的三类安定特性表现如下:A类(塑性安定状态),累积应变曲线呈快速收敛型,竖向永久应变率随着竖向应变的发展迅速降低,且单位体积耗散能始终稳定在较低水平,表明在有限次循环荷载作用下,路基填料处于塑性安定状态,只发生可恢复的回弹变形,而塑性永久应变不再发展;C类(增量破坏),累积应变曲线呈快速上升发散型,竖向永久应变率随着竖向应变的发展趋于稳定值不再下降,单位体积耗散能波动上升,表明在有限次循环荷载作用下,路基填料的永久变形将持续发展直至破坏;B类(塑性蠕变),是一种A类与C类之间的中间状态,累积应变曲线呈缓慢上升型,在起始循环荷载作用下永久应变率维持在较高水平,而后应变率降低并保持不变,单位体积耗散能大致处于较高水平且略微上升,表明在有限次循环荷载作用下,路基填料处于永久变形缓慢发展的状态,直至最终破坏。
基于前述分析,在三类安定状态之间,存在着某一临界阈值,当动应力、动应变水平超出限值后,填料的长期变形发展模式和稳定状态将会发生改变。通过确定填料不同安定状态间的临界阈值,即可判断预测在该应力、应变水平下填料长期变形的发展趋势及收敛稳定性。对于高速铁路路基结构设计,当总应变足够小时,A类的塑性安定状态是允许,而C类状态是严格禁止的。为保证路基填料等岩土材料在交通荷载等循环动力作用下的长期耐久稳定,需要使其尽量处于变形能够短期收敛稳定的安定状态。因此,构建填料长期变形演化规律与安定状态的关联,并确定三种状态间的临界阈值判别标准,是控制填料变形长期稳定的关键前提,具有重要的理论和实践意义。
4 安定状态判别标准与临界阈值分析
4.1 基于单位体积耗散能的安定临界状态判别标准
岩土体材料的损伤劣化与其内部能量的耗散密切相关[43]。填料受到长期循环荷载作用时,每个周期的耗散能实质表征了外力作用下不可恢复的应变能量,在耗散能产生的同时填料内部由初始状态逐步出现塑性变形和残余应力应变,这种变化可以理解为能量耗散引起的不可逆劣化或损伤,累积后将成为填料由稳定状态向不稳定状态乃至最终破坏的诱因。这与安定理论中应力-应变行为呈现出的不同安定状态存在较好的理论对应性:弹性状态没有塑性耗散能的产生,每个循环的单位体积能均由弹性能组成;塑性安定状态则是每个循环产生较少的塑性耗散能,同时该部分塑性耗散能基本维持不变;塑形蠕变状态对应与较高的耗散能水平,同时在较高振次时逐渐增加;增量破坏状态则为快速增加的耗散能,对应于填料在短时间的劣化和破坏。因此,本文通过构建耗散能与安定状态间的理论关联,作为判断临界阈值的依据。
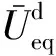
( 2 )
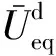
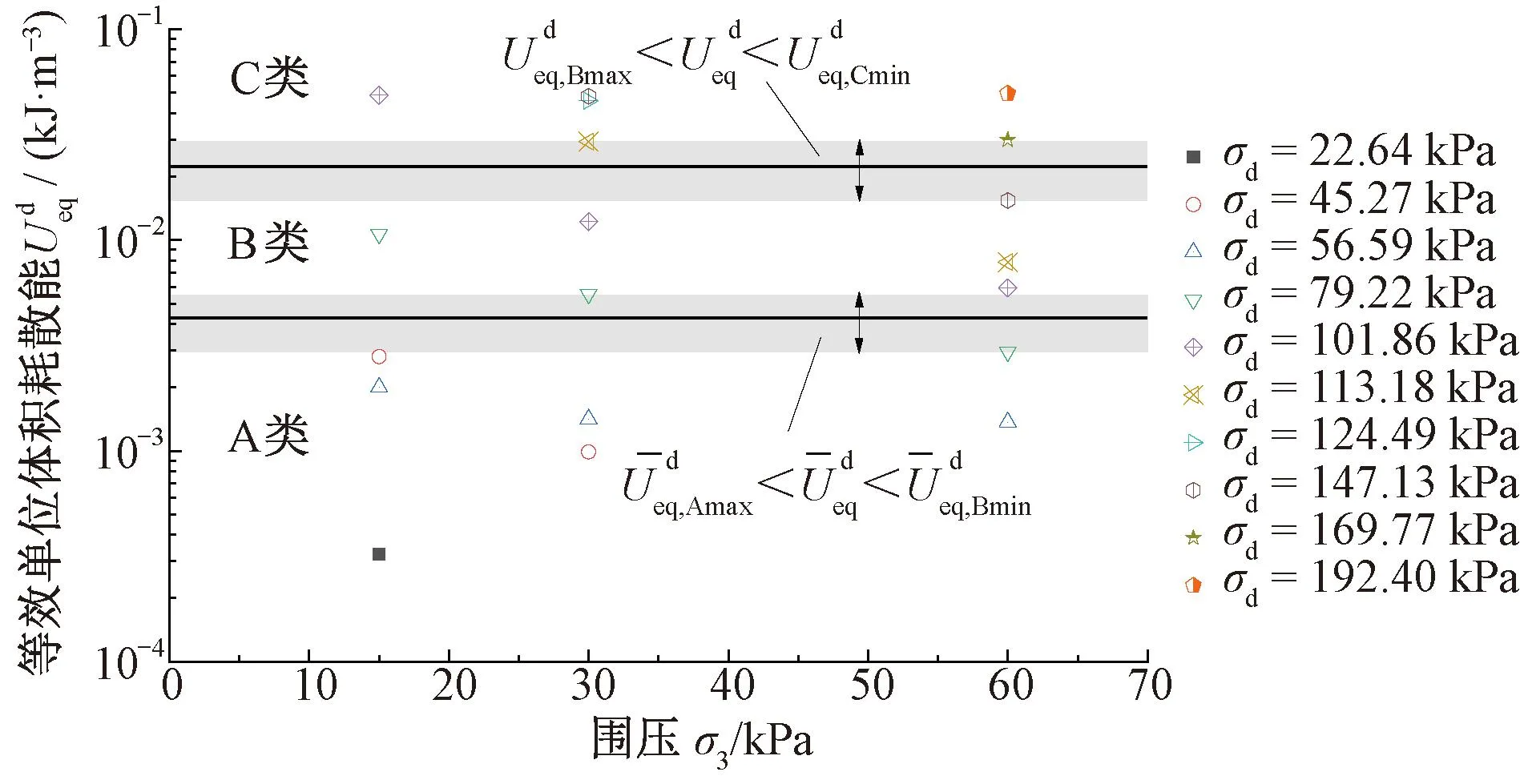
图13 基于单位体积耗散能的安定状态分区
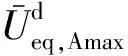
( 3 )
( 4 )
( 5 )
式中:λA-B、λB-C分别为对应于A-B状态间以及B-C状态间的等效单位体积耗散能临界值,对于本文研究的典型高铁路基填料,λA-B= 4.25×10-3kJ/m3,λB-C= 22.36×10-3kJ/m3。不同填料类型和加载试验条件可能会对该量值产生影响,但上述判别准则及阈值计算方法依然适用。
为对比验证本文阈值判别方法的有效性,另采用Werkmeister等[29]提出的累积应变率界限法获取的经验值进行分析。该方法主要依据加载曲线中3 000~5 000 次循环这一阶段应变速率对安定状态进行判别,相应准则为
( 6 )
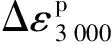
基于累积应变率界限法的安定状态分区见图14。由图14可见,该方法获取的安定状态分区数据点与通过单位体积耗散能获取的分区数据点规律近似,围压15、30 kPa下获取的阈值较本文方法略低,围压60 kPa下则获取了相同的分区结果,对应阈值判定一致。对比结果说明本文的安定阈值判别准则是有效的。
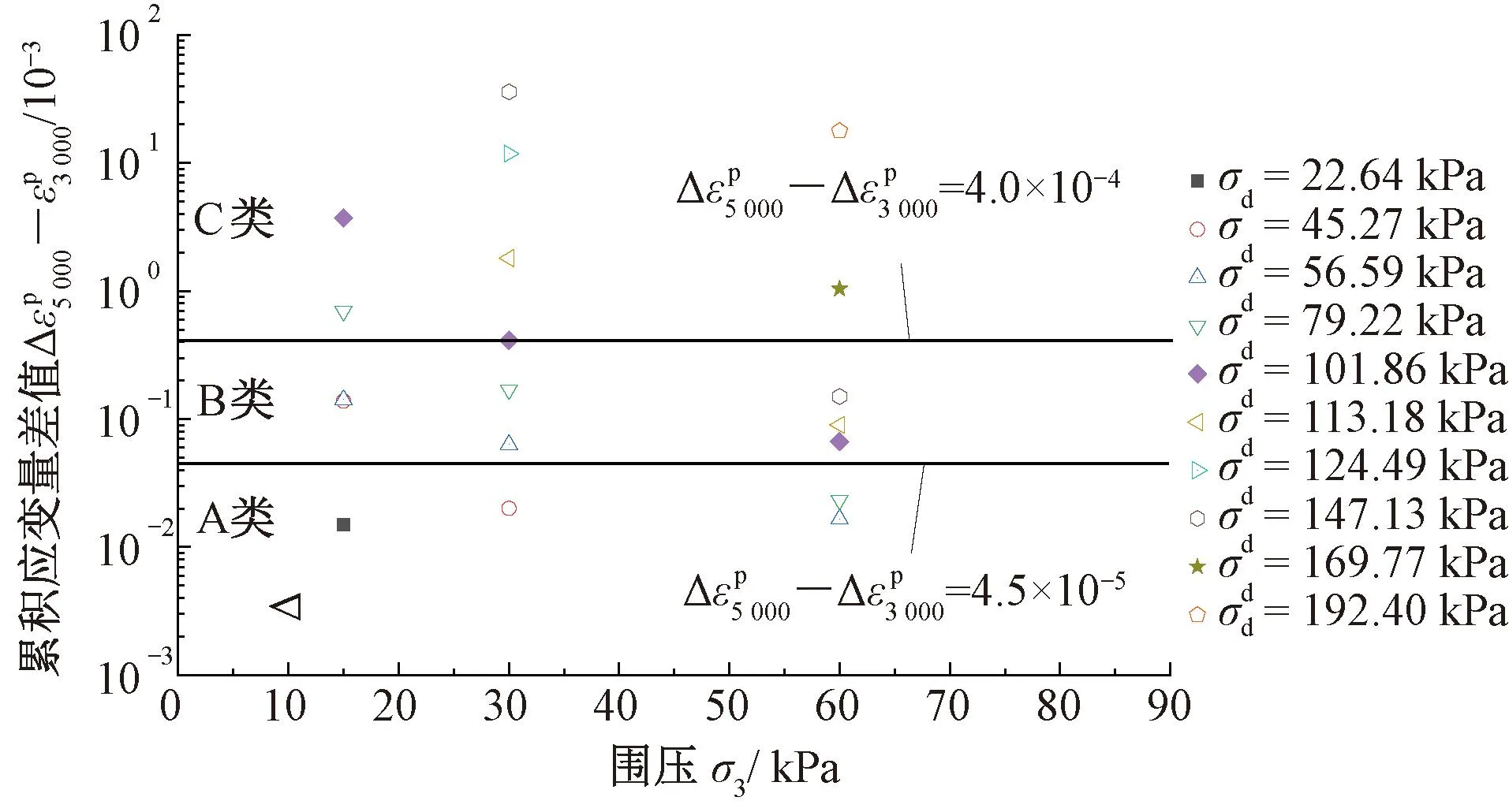
图14 基于累积应变率界限法的安定状态分区
相较于应变率界限方法,本文方法不但考虑了应变累积表观规律的差异,还可反映不同阶段填料能量耗散的平均水平及变化趋势,同时不依赖于特定加载次数区间应变或应变率数据,避免了仅用少量特征点进行判断的局限性,指标选取更为合理,适用于不同加载次数、加载模式和填料类型。
4.2 路基填料安定临界条件分析
依据式( 3 )提出的基于单位体积耗散能的安定临界状态判别准则,单位体积耗散能和动应力幅值的关系曲线见图15,并在图中标注判别临界值常数的准则线(虚线所示)。由图15可见,计算累积应变量差值和动应力幅值的关系曲线与单位体积耗散能临界值常数线相交位置的动应力幅值,其代表了由A塑性安定状态转变为B塑性蠕变状态以及C增量破坏状态的临界点,即视作对应围压条件下的A-B临界动应力幅值以及B-C临界动应力幅值。
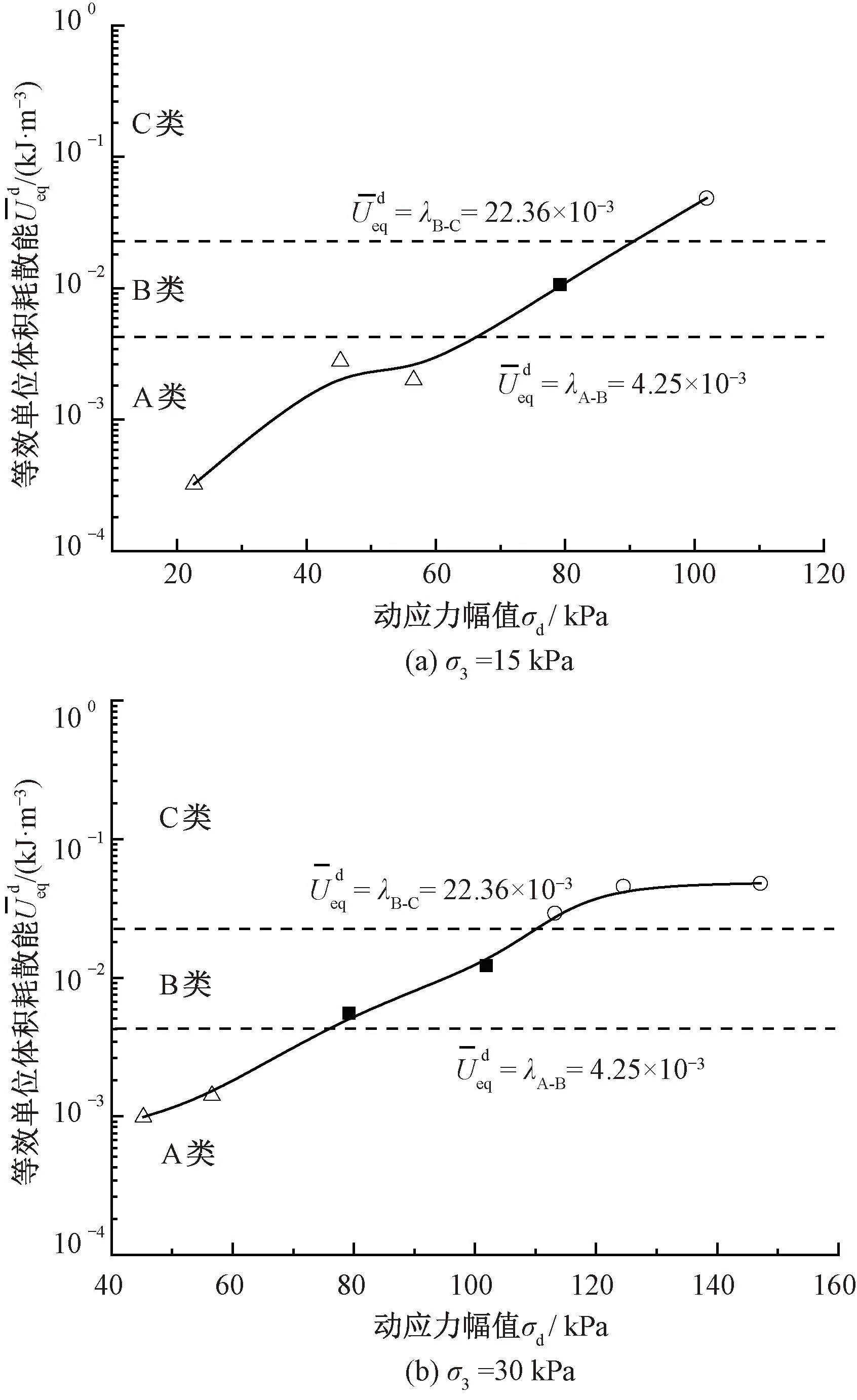
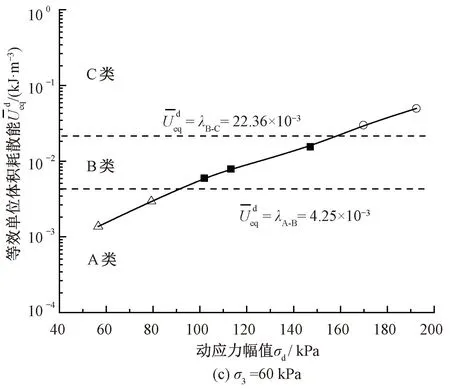
图15 单位体积耗散能与动应力幅值关系曲线
同样的,针对不同的试验条件下的动应变幅值,计算累积应变量差值和动应变幅值的关系曲线与临界值常数线相交位置的动应变幅值,视作对应围压条件下的A-B临界动应变幅值以及B-C临界动应变幅值,见图16。
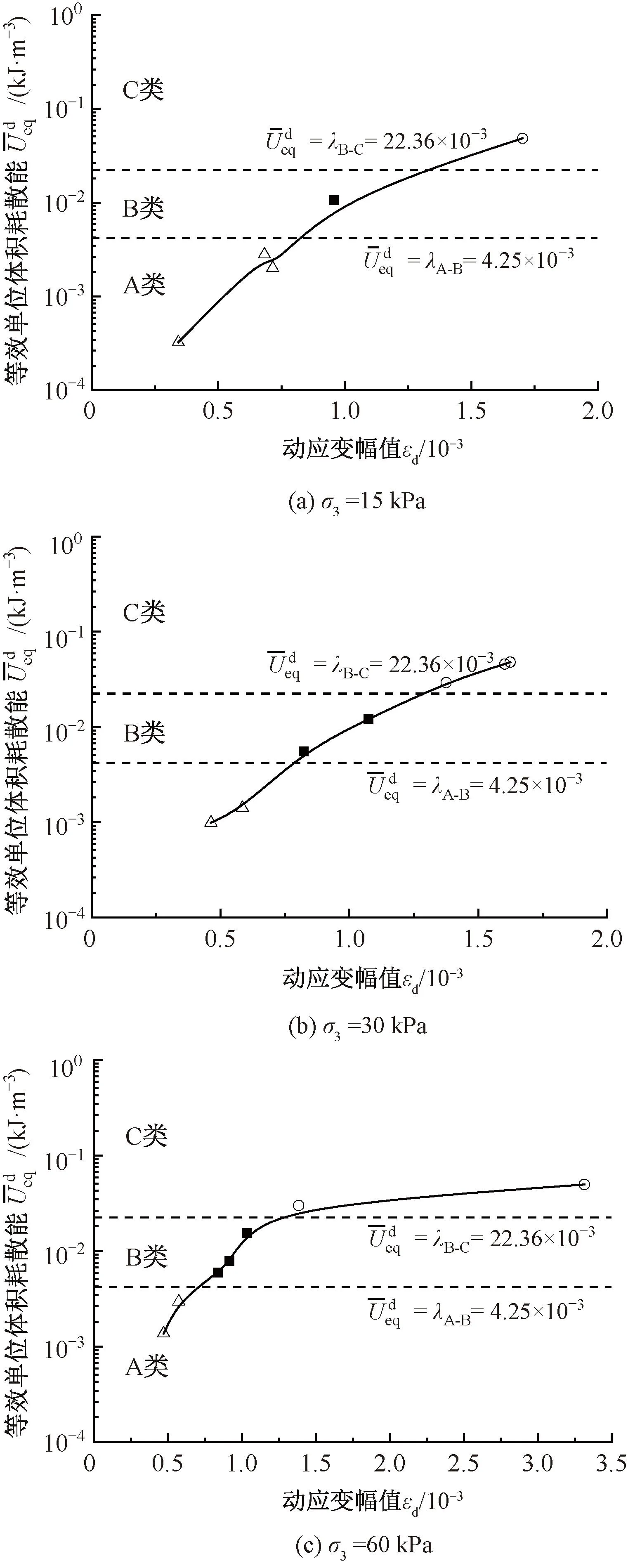
图16 单位体积耗散能与动应变幅值关系曲线
为定量分析高铁路基粗粒土填料的动应力安定临界条件和相应的安定阈值,定义循环应力比CSR为
CSR=σd/2σ3
( 7 )
通过此无量纲参数,结合各试验条件下累积应变量差值对应的临界动应力幅值,绘制塑性安定、塑形蠕变、增量破坏三类变形状态在循环应力比-围压应力空间中的数据点,并给出A-B、B-C状态间的临界阈值曲线,见图17。
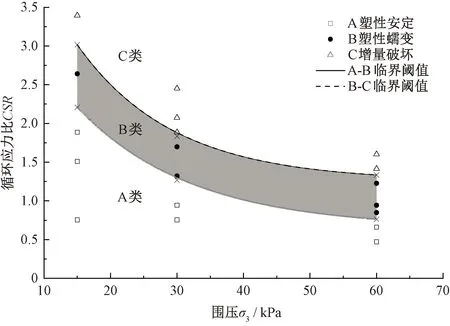
图17 填料动应力安定临界阈值曲线
由图17可见,不同围压和动偏应力条件下,塑性安定、塑性蠕变、增量破坏三类变形状态间存在一临界循环应力比范围。处于A-B临界阈值曲线左下方为塑性安定状态,处于B-C临界阈值曲线右上方区域的即为增量破坏状态,处于两者之间阴影区域的为塑性蠕变状态。
利用指数函数形式对高铁路基粗粒土填料的临界循环应力比阈值曲线进行拟合,拟合计算式为
CSR=Aexp(-tσ3)+C0
( 8 )
式中:A、t、C0均为阈值曲线相关参数,A、t与临界循环应力比随围压的变化幅度及曲线倾斜程度相关,C0则代表了零围压的无侧限条件下的临界循环应力比阈值。对于本文所研究填料,相关参数取值见表2。

表2 临界循环应力比阈值曲线参数取值
由图17可见,虽然CSR量值随围压增大呈下降趋势,但实际上动应力安定临界阈值随围压仍然是增加的,根据换算关系,60 kPa围压条件下阈值较15 kPa围压下阈值增加约38%,这表明围压的增加将显著增加填料的动力安定性。因此,高铁路基基床临近表层的填料相较下部基础更易在较高的外部动荷载作用下诱发稳定性的降低和长期变形的累积;同时路基施工过程中需对填筑质量等严格控制,确保填料所处位置围压条件、压实度等满足要求。
同样的,对动应变幅值的临界阈值曲线进行分析,见图18。
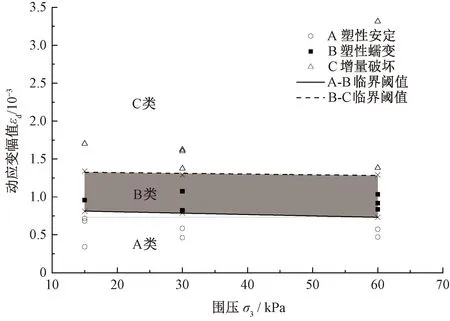
图18 填料动应变安定临界阈值曲线
利用线性函数形式对高铁路基粗粒土填料的临界动应变阈值曲线进行拟合,拟合计算式为
εd=kσ3+εd0
( 9 )
式中:k、εd0为阈值曲线相关参数,其中k与临界动应变阈值随围压的变化幅度相关,εd0则代表了零围压的无侧限条件下的临界动应变阈值。对于本文所研究填料,相关参数取值见表3。

表3 动应变安定临界阈值曲线参数取值
相对于动应力幅值,动应变的临界阈值曲线更趋向于线性,且斜率较小(10-3~10-4量级)。在本研究涉及的围压范围内,根据B塑性蠕变状态的阴影区域所处的动应变幅值范围,可以得出结论:引起高铁路基填料由稳定的安定状态向不稳定的增量破坏状态的临界动应变范围大致处于0.8×10-3~1.3×10-3。为确保高铁路基的长期耐久稳定,需要将基床填料的动应变量值控制在此临界值以下。
5 结论
本文基于循环动力作用下典型高铁路基粗粒土填料长期变形试验,研究了应力-应变关系、塑性应变率、耗散能变化等与不同安定状态之间的关联,分析了路基填料的长期变形发展模式,给出了基于等效单位体积耗散能的安定临界条件判别标准与动应力、动应变安定阈值。可得到以下结论:
1)循环动载作用下填料长期变形的三类发展模式分别对应于不同的永久变形收敛性、应变累积率曲线形态以及耗散能变化规律。其中A类试样应变累积速率随永久变形量的增加快速下降,单位体积耗散能稳定在较低水平;B类试样应变累积速率缓慢下降,单位体积耗散能一定循环次数后呈现轻微上升趋势;C类试样应变累积速率维持在较高水平,单位体积耗散能较大且随加载次数的增加呈现波动上升。
2)提出了以等效单位体积耗散能为指标的安定临界状态判别准则,对于本文研究的高铁路基粗粒土填料,等效单位体积耗散能判别准则临界值分别为4.25×10-3kJ/m3(A-B)以及22.36×10-3kJ/m3(B-C)。
3)围压的增加将增加填料的动应力安定阈值。动应变的临界阈值曲线更趋向于线性,且斜率较小(10-3~10-4量级)。在本研究涉及的围压范围内,引起高铁路基填料由稳定的安定状态向不稳定的增量破坏状态的临界动应变范围为0.8×10-3~1.3×10-3。

