基于集合神经网络的水文站洪水预报研究

戎丹雅，汤 斌

(1.浙江省水利水电勘测设计院有限责任公司，浙江 杭州 310000；2.浙江大禹信息技术有限公司，浙江 杭州 310000)

根据世界气象组织1970年至2019年统计数据，洪水是发生最频繁且最具破坏性的自然灾害之一，占全球气候相关灾害总数的44%。洪水预报是最有效的降低灾害影响的策略之一，因此准确可靠地预测洪水过程对于一个国家或地区来说极其重要。

模拟复杂的非线性暴雨-洪水过程，通常采用两类建模框架：传统水文模型和机器学习水文模型。谢尔曼在1932年提出流域单位线水文理论，为水文预报发展奠定了基石，新安江模型普遍应用于湿润和半湿润地区，TOPKAPI分布式水文模型被广泛用于无资料地区。传统水文模型中有诸多参数需要率定，无法直接获取，会影响预报的准确性。

随着水利信息化建设的推进，水文资料日益丰富，机器学习水文模型人工神经网络(ANN)因其在解决非线性问题方面的良好性能，在洪水预报、水位预报领域得到了广泛的应用。BP神经网络作为人工神经网络代表算法之一，在2014年于中国洪水预报系统应用中获得较高的预报精度。然而单一BP神经网络模型泛化能力较弱，结合集合预报技术，集合神经网络将增加预测结果的可靠度。

本研究致力于构建集合神经网络模型(EANN)，以浙江省钱塘江流域上游山区开化水文站为研究对象，以1966—2017年期间等6场降雨洪水资料为依据，尝试采用参数初始值扰动随机产生多组集合参数，每组集合参数计算求得洪水过程，再分别通过简单平均、贝叶斯平均和Stacking平均3种方法对洪水过程进行集合预报。相较于单一BP神经网络模型，集合神经网络模型在洪水预报效果方面有较大优势。

1 研究区域和数据资料

本文以浙江省衢州市开化县第一个国家基本水文站——开化水文站作为研究对象。开化水文站位于浙江省钱塘江流域上游马金溪，集水面积为816km2。地形以丘陵为主，整个地势由西北向东南逐渐变低。全年降雨主要集中在4—10月，最大月降雨一般出现在4—7月梅雨期，降水时间分布不均且降雨强度大，河道比降7.1‰，是洪水频发区，洪峰持续时间短，一场洪水历时5—7日。

为了更加准确地模拟洪水过程，本文采用3种不同集合神经网络模型对开化水文站洪水分别进行模拟。采用资料包括开化水文站6场洪水及其以上流域内雨量站降水资料等，率定期选定4场洪水，检验期选定2场洪水，时间尺度为小时。流域内雨量资料较为丰富，且域内分布合理，能反映流域暴雨特征。选取齐溪、燕溪、皇林坑、马金、大溪边和密赛6个国家基本雨量站降水数据，流域研究范围及站点位置分布如图1所示。

图1 研究区域站点分布图

2 研究方法

2.1 影响因子筛选及数据归一化处理

影响因子筛选准确、全面与否，是准确模拟洪水工作的前提。集合神经网络模型为黑箱模型，影响因子不考虑物理机制相关要素，综合考虑洪水成因及模型结构复杂情况，其次通过相关系数法筛选影响因子，即作为模型的输入项。模型输入项为开化站不同时刻流量Q(t-3、Q(t-2、Q(t-1、Q(t)和流域不同时刻面雨量P(t-4、P(t-3、P(t-2、P(t-1、P(t)，输出项为开化站Q(t+1)，t为小时单位。

收集筛选得到开化水文站历史大洪水共6场，挑选出4场洪水作为模型率定，2场洪水用于模型验证。流域逐时面雨量由6个雨量站点的泰森多边形法加权平均计算得到。为了方便计算所有数据统一归一化处理。

2.2 预报模型构建

集合神经网络模型是在BP神经网络对参数初始值进行扰动的基础上再分别用简单平均、贝叶斯平均和Stacking平均3种方法进行集合模拟。

步骤1模型结构及节点数确定。本文采用应用最广泛的BP神经网络结构，包含输入层、隐含层、输出层3层结构。输入层节点数9个，输出层节点数1个，目前没有成熟的理论依据计算隐含层节点数，一般采用试算法，若训练结果一直无法收敛，则增加节点数，若已收敛但仍达不到较好预报效果，则减少节点数，本研究试算得到隐含层节点数5个。

步骤2网络参数初始值扰动。训练函数选用trainlm函数，学习函数选用learngdm函数，传递函数选用tansig函数，训练次数设置在1000～10000区间，学习速率设置在0.001～0.1区间，目标误差设置为0.1。采用参数初始值扰动随机产生多组集合参数，多次反复试验并综合确定15组集合参数效果较佳。

步骤3洪水集合预报。使训练集不断率定每组集合参数到最佳状态，每组集合参数对应一组洪水模拟值。15组洪水模拟值分别通过简单平均、贝叶斯平均和Stacking平均3种方法进行集合预报，最终得到1组集合预报值。

步骤4网络模型验证。使验证集采用率定参数对2场洪水进行模拟，根据模拟精度评判模型预报效果。

2.3 贝叶斯模型平均(BMA)

贝叶斯模型平均(Bayes Model Averaging)是给每个模型赋予权重，并通过加权平均确定最终的预测值。BMA根据先验信息估计先验分布、根据样本信息构建似然函数，结合贝叶斯定理就得到后验分布，即得到每个模型赋予的权重，主要计算步骤如下。

第一步：通过BOX-COX函数对实测值和预测值进行正态变换，以便后续计算。

第二步：计算神经网络模型后验概率，即模型权重：

(1)

式中，D={y1，y2，…yn}—实测资料即流量数据，y—预报变量；M={m1，m2，…mk}—模型空间，即包含k个模型集合成员；P(mi)—最优模型的先验概率，一般取均匀分布，P(y|mi)—似然函数。各模型权重之和为1。

第三步：计算预报变量概率密度函数：

(2)

式中，P(y|mn，D)—模型mn和数据D条件下预报变量的后验概率。

第四步：计算集合预报结果：

(3)

式中，E(y|D)—集合预报值，模型的权重可代表对集合预报值的相对贡献程度，且权重具有动态性，随着实测资料的不断更新延长，使得预报精度不断提高。

2.4 Stacking平均

Stacking一般采用两层结构，第一层多个基学习器分别输出特征，第二层元学习器根据输出特征给出最终的预测结果。Stacking模型既能有效防止过拟合现象，又不会丢失原始数据集的特征。最初训练集和测试集分别作为m个基学习器的输入条件，进行交叉验证，然后对训练集的估计结果进行垂直合并，生成新训练集；对测试集进行多次预测相加取平均，生成新测试集。将新训练集输入元学习器中进行训练，使用新测试集评估模型。

元学习器使用实测值与预测值之间的平方相对误差进行评估，即采用下式：

(4)

(5)

式中，ck—用于整合预报输出得到最终均值预报。

3 结果对比分析

3.1 洪水模拟结果分析

集合神经网络模型用简单平均、贝叶斯平均和Stacking平均3种方法进行集合模拟，对应3类模型工况分别为EANN1、EANN2、EANN3。选取的洪水样本具有一定代表性，既有单峰型也有双峰型、洪峰流量最小900m3/s，最大2000m3/s。率定期采用1974年6月14—20日、1983年5月29日—6月4日、1995年5月28日—6月3日和2010年6月16—23日共4场洪水训练模型参数，验证期采用2011年6月13—19日、2017年6月22—28日共2场洪水对开化水文站的洪水过程进行模拟。对比6个场次洪水的实测与模拟过程，如图2所示。可以看出，在率定期洪水实测过程与模拟过程演变趋势相似，且对峰值大小和峰现时间模拟效果较好，其中1974年和1995年模拟效果最好；但对低流量模拟不佳，低流量时模拟值时而偏大时而偏小。

图2 开化站洪水实测与模拟对比过程图

为了更精确地评价集合神经网络模型的准确性，本文采用3个集合神经网络模型对6场洪水逐一进行精度评价，选取确定性系数(Dc)和合格率(QR)2个精度评价指标，评价结果见表1。可以看出，在率定期和验证期流量峰值误差绝对值均小于20%，且EANN2在1974年场次中达到最小误差为5.19%；在率定期峰现时间错时介于2h以内；确定性系数均大于0.70，部分场次洪水确定性系数甚至高达0.96；合格率均高于70%，预报效果整体较好。

表1 集合神经网络模型计算结果

3.2 与单一BP神经网络模拟结果对比

为了充分验证集合神经网络模型预报效果优于单一BP神经网络模型，采用单一BP神经网络模型对同6场洪水数据进行参数率定和验证，且为了保证可比性，BP神经网络模型结构与集合神经网络模型结构一致。

选取3个精度评价指标为峰值绝对误差均值、确定性系数均值和合格率均值，对比结果见表2。从表里可以看出，集合神经网络的峰值绝对误差均值在率定期和验证期均小于20%且最小为6.8%，单一BP神经网络均大于25%；集合神经网络确定性系数均值在率定期和验证期均大于0.8且集合神经网络(贝叶斯平均)模型在率定期达到0.95，单一BP神经网络均小于0.65；集合神经网络合格率均值在率定期和验证期均大于70%且最高达到85%，单一BP神经网络均小于66%；相较于验证期，各模型均在率定期达到较好的预报效果，因洪水场次不足在一定程度上会影响预报效果，未来可增强洪水场次代表性。

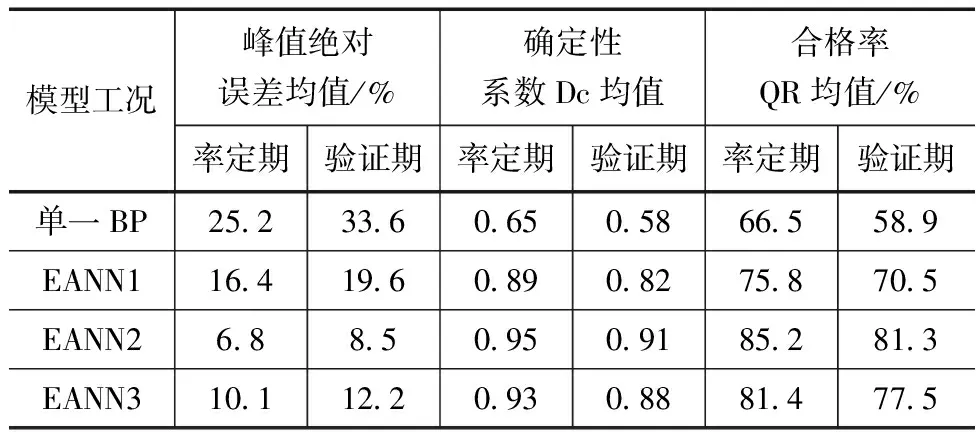
表2 模型精度对比结果

综上，对6场洪水进行模拟，单一BP神经网络模型的表现明显差于集合神经网络模型.集合神经网络(贝叶斯平均)模型模拟效果最佳，单一BP神经网络模拟效果最次。集合神经网络(贝叶斯平均)模型会给予较优模型更大权重，整合预报效果也会比简单平均和staking平均更优，合格率均值80.0%～85.0%，确定性系数均值0.91～0.95，根据GB/T 22482—2008《水文情报预报规范》中要求可达到甲级预报精度标准，可用于作业预报，相较于单一BP神经网络模型丙级精度有较大提高，分析原因是集合技术有效提高了BP神经网络泛化能力。

4 结语

本文以开化水文站为研究对象，采取神经网络与集合预报结合的思路对洪水预报进行研究，得到结论如下。

(1)根据洪水成因及模型结构复杂程度考虑，确定影响因子，对参数初始值的扰动基础上进行集合预报，构建3种集合神经网络模型，此模型应用简便，洪水预报效果较好，是一种值得继续研究的模式。

(2)相较于单一BP神经网络模型，集合神经网络模型洪水预报的整体效果较好。集合神经网络(贝叶斯平均)模型的合格率均值80.0%～85.0%，确定性系数均值0.91～0.95，可达到甲级预报精度标准，可用于作业预报。

(3)模型仍有诸多的提升空间。集合预报模型对低流量模拟效果不稳定，未来可尝试对低流量单独进行影响因子识别筛选；另外，本文模型是针对开化水文站及上游流域特征而建立的洪水预报模型，较适合山区性小流域洪水预报，若应用于其他类型区域，必须重新调整模型，未来可考虑增加平原地区模块，以增强模型的通用度。