系统性金融风险对宏观经济运行的非线性影响研究

曾骁昳

在全球经济和金融综合化、我国金融对外开放深化的大背景下，系统性金融风险逐渐成为影响经济稳定的重要因素［1-2］。从20世纪末的亚洲金融危机到2008 年的全球次贷危机，再到2015年的我国股市暴跌，每次金融领域的动荡都直接冲击到了我们的实体经济［3-4］。因此，防范和处理系统性金融风险成为国内外研究者和金融监管部门的首要任务。但是，在瞬息万变的金融环境中，如何准确地量化和评估系统性金融风险仍是一大挑战［5-6］。再者，还需要对系统性金融风险对宏观经济产生的影响有一个全面深入的认识，这样才能在宏观经济发展遇到困扰时做出正确的应对策略。大多数关于系统性金融风险和宏观经济的研究是通过格兰杰因果检验来研究二者之间的关系。此外，对于经济韧性大多研究区域、省域或城市经济韧性水平，研究整体宏观经济韧性并将其作为宏观经济重要指标来研究系统性金融风险对宏观经济的非线性效应的较少。因此，研究计划通过各金融子市场选取的18个关键指标，运用CRITIC法和因子分析法，构建系统性金融风险指数（Systemic Financial Risk Index，SFRI），以此定性和定量地评估我国系统性金融风险的水平。同时，采用MS-VAR模型探讨系统性金融风险对宏观经济的非线性影响，对防范系统性金融风险、完善宏观调控政策具有重大意义。

一、研究方法

（一）系统性金融风险与宏观经济韧性水平指数构建

在进行系统性金融风险对宏观经济运行的非线性影响研究时，首先构建一个系统性金融风险的衡量系数以及一个宏观经济的抗压能力的衡量指标。然后使用MS-VAR 模型分析系统性金融风险对宏观经济运行的非线性影响。为了构建SFRI，研究选择了六大金融子市场：银行、股票、债券、外汇、保险和房地产，并选取了这些市场的18 个具有代表性的指标［7］。系统性金融风险指标如图1所示。

图1 系统性金融风险构建指标

宏观经济抗压能力，就是指一个经济体对外界打击的抵抗力和恢复力。它不仅和一个国家的经济增速和经济规模有关，而且和经济结构是否合适、经济创新活力和对新情况的适应能力等多个方面都息息相关。本研究从经济稳定性、经济多样性、经济创新性以及经济恢复能力四个维度选择了13个关键指标来构建宏观经济抗压水平指标［8-9］。通过构建各维度指数并进行赋权，进而综合测算出宏观经济韧性水平指数（Macroeconomic Resilience index，MR）。宏观经济韧性水平指标如图2所示。

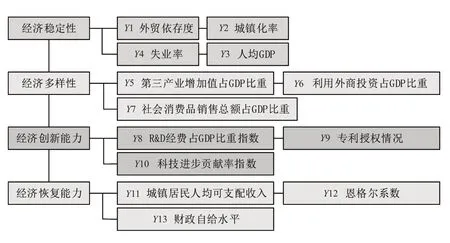
图2 宏观经济韧性水平构建指标

在进行指数计算时，不仅要考虑到指标体系的选取，还需要综合考虑各指标的权重。本研究采用CRITIC 法与因子分析相结合的方法，对系统财务风险和宏观层面的影响因素进行测算。CRITIC 法考虑了变量之间的内在冲突，因此更为合理。CRITIC法通过指标间对比强度和指标冲突性来衡量指标的信息量，即单个指标在整个指标体系中的作用，然后根据信息量的大小进行指标赋权。指标间对比强度也叫指标间的变异程度，主要用标准差来表示，如公式（1）所示。

公式（1）中，xij为第i个样本第j项指标的数值，n为样本的数量。 -xj为第j项指标的均值，Sj为第j项指标的标准差。指标冲突性Rj的计算如公式（2）所示。

公式（2）中，p为指标的数量，rij为第i个指标和第j个指标的相关系数。使用CRITIC法计算第j个指标的权值如公式（3）所示。

公式（3）中，wj和Cj分别是第j个指标的权重和信息量。因子分析法是对主成分分析法的进一步发展，它可以将具有重叠信息或错综复杂关系的变量简化为少数几个无关的综合因子。该方法构建多个具有较高权重但彼此独立的因素，有效解决了多变量共线性的问题。此外，因子分析更加注重各指标之间的相关性，其优势之一是可以减弱因素之间的相关性，从而减少因素数量。研究对指数的测算分为两部分：第一部分运用因子分析方法，对各因素进行衡量和测度，确定各因素对风险的影响程度。第二部分运用CRITIC 赋权方法计算各维度的权重，并得到SFRI和MR。在此基础上，使用两倍标准差作为界限，计算风险识别系数，如公式（4）所示。

公式（4）中，CFS2t是两倍标准差代表的风险识别系数。若系数大于1，则表明发生系统性金融危机的风险水平为重度，极有可能或已经发生金融危机；若结果在［0，1］之间，则表示系统性金融危机的风险水平为中度，有较小的可能发生危机；若系数小于0，则表明风险水平为轻度，发生系统性金融危机的可能性极小。

（二）基于MS-VAR模型的宏观经济非线性效应研究

MS-VAR 模型是在马尔可夫区制转移模型的基础上结合向量自回归模型建立的。该模型可以反映多时间序列变量间的非线性因果关系，模型参数估计结果会随变量系统的状态改变而变化，从而能够更好地描述变量之间在不同区制状态下的动态关联，这也更符合经济学领域变量间非线性特点的实际［10］。在MS-VAR模型中，引进状态参数St来控制各状态之间的切换，同时也是对变量之间的非线性关系进行建模的核心点。MS-VAR 模型的一般形式如公式（5）所示。

公式（5）中，yt表示时间序列向量，μ(st)表示截距项，用来描述参数对实现的状态st的依赖性。Aj为自回归系数矩阵。εt表示误差项，服从多元正态分布。st∈(1,2,…,M)表示不可观测的区制变量，服从一个不可约的、遍历M区制的马尔可夫随机过程。从区制到区制的转移概率pij，如公式（6）所示。

研究借助Givewin2.0 软件进行MS-VAR 模型的估计，利用极大似然估算法进行模型参数的估计。该方法不但可以求出模型各时期的参数和转移矩阵，而且可以计算各时期处在某种状态的可能性，并绘制出状态转移概率图。研究将建立SFRI、MR与宏观经济景气指数（Macro-economic Climate Index，MCI）三变量的MS-VAR模型，来探讨在不同区制状态下，系统性金融风险对宏观经济的非线性效应。MCI是取对数后的宏观经济景气一致指数。

二、研究过程

在SFRI和MR的基础上，本文将主要围绕系统性金融风险对宏观经济影响的非线性效应进行实证研究。实证分析过程中，系统性金融风险指标和宏观经济韧性指标的样本数据来源于Wind 数据库和国家外汇管理局官网，研究选取了2004 年1 月—2021 年4 月的月频指标数据。在使用MS-VAR 模型分析不同风险状态下系统性金融风险对宏观经济的非线性影响时，首先需要确定模型的最佳滞后阶数和区制数量。研究使用对数线性准则（log-Likelihood，LogL）、赤池信息准则（Akaike information criterion，AIC）、最终预报误差准则（Final Prediction Error Criterian，FPE）、施瓦茨准则（Schwarz criterion，SC）和汉南·奎因准则（Hannan Quinn，HQ）等信息准则作为判断依据，进行MS-VAR模型的最佳滞后阶数选择，如表1所示。

表1 不同阶数的MS-VAR模型信息准则评价结果

根据表1可知，当选择4阶时，FPE和AIC都是最好的，所以MS-VAR模型的最佳滞后阶数确定为4 阶。国内外对经济周期不对称问题的研究常采用两区制的MS-VAR 模型，将其分为“低风险”和“高风险”两种状态。图3展示了二区制MS-VAR模型的区制概率。

图3 MS-VAR模型不同区制的概率分布

从图3可以观察到，系统性金融风险对宏观经济的影响存在明显的两区制结构，并将样本期划分为高风险状态和低风险状态。在区制1 的时间段（主要包括2005—2008年、2010—2016年的大多数月份以及2017—2021 年的大部分月份），SFRI较低，MR和MCI波动平稳，宏观经济运行平稳。而区制2的时间段（主要包括2005年汇率改革后、2008—2009 年、2010 年、2013 年的个别月份，2015—2017年股市崩盘、汇率制度改革和熔断机制、美元加息等金融波动期，以及2018 年中美贸易战、2019 年和2020 年个别月份），金融业发生了一些震动，风险传染效应使系统性金融风险水平升高，并进一步传导到宏观经济层面，MR和MCI波动较大。因此，可以认为这两个区制对应着不同的系统性金融风险状态，且自2013年以来我国经济进入高风险状态的频率显著增加。不同区制间的转换概率如表2所示。

表2 不同区制间的转化概率

从表2 中可以看出，在区制1（风险水平低）的情况下，持续处于危险状态的概率为0.918；而在区制2（风险水平高）的情况下，保持在高风险状态的概率为0.625。这表明，对于这两个不同的区域体系，在没有发生重大的外部影响的情况下，体系将保持相对稳定的状态。此外，从图3 中可以看出，高风险区主要集中在2008 年次贷危机后，尤其是2013 年之后。随着国际形势的变化，我国经济步入了“新常态”，金融风险频繁发生，这会对我国宏观经济的恢复能力、人们的预期以及经济运行情况产生一定影响，进而导致宏观经济波动加大。为了更加清晰地对比不同风险状态下系统性金融风险水平对宏观经济的影响是否具有非线性效应，研究将MSVAR 模型按不同区制分别进行参数估计。MSVAR模型区制1的参数估计结果如表3所示。

表3 MS-VAR模型区制1的参数估计结果

从表3 可以看出，在低风险状态下，系统性金融风险对MCI和MR的影响都没有显示出显著性。然而，SFRI、MR和MCI三者对自身的影响都表现出了显著的正向联系。具体而言，从结果可以看出，滞后1 期的SFRI对当期SFRI有显著的正向影响（系数为0.479，在1%置信水平下显著）。这意味着，在低风险状态下，金融风险在过去一段时间的表现在一定程度上影响了其在现期的表现。同时，滞后1 ∼3期的MCI对当期MCI都有显著的影响，但是影响的方向取决于滞后期数。特别的，滞后1期时，MCI对当期是显著的正向影响（系数为1.702），而在滞后2期和滞后3 期时为显著的负向影响（系数分别是-0.655和-0.308）。这一结果表明，经济景气因素在短期内可能通过正向反馈机制进行自我强化，但在中长期则可能存在反向调节。此外，滞后1期的MR对当期MR有显著的正向影响，系数为0.575。这表明在低风险状态下，经济韧性有一定的持续性，即过去的经济韧性能够在一定程度上影响现期的韧性。MS-VAR 模型区制2 的参数估计结果如表4所示。

表4 MS-VAR模型区制2的参数估计结果

从表4中可以看出，区制2状态下，系统性金融风险对宏观经济运行有明显的影响。从SFRI、MR、MCI三变量的方程系数来看，1%显著性水平下，无论是滞后1期还是滞后3期的SFRI对当期自身都具有正向显著影响，系数分别是0.925 和0.760。滞后1 期和滞后4 期的MR对当期自身的正向影响也都具有显著性，系数分别是0.641和0.701。滞后1期的MCI也对当期自身存在显著正向影响，系数为1.227。区制2 参数估计的结果说明，SFRI、MR和MCI在高风险水平下仍然具有一定的惯性。研究对MS-VAR 模型进行了有效性验证，模型结果的拟合与残差分布如图4所示。

图4 MS-VAR模型结果的拟合与残差分布

从图4 中可以看出，MS-VAR 模型能很好地反映系统性金融风险与宏观经济两变量的变化。其中，图4（a）、4（c）、4（e）描述了SFRI、MR、MCI的实际值、平滑值和一步预测值的关系。图4（b）、4（d）、4（f）描述了MS-VAR 模型实际残差的正态分布拟合结果。验证结果证实了MSVAR 模型被运用在研究系统性金融风险对宏观经济非线性效应中的有效性。

三、结论

为了分析我国经济的系统性金融风险水平和变化，并探讨该类风险对宏观经济的非线性影响，研究使用CRITIC法和因子分析法，综合应用18 个关键指标来构建SFRI，并使用MS-VAR 模型分析不同区制状态下系统性金融风险对宏观经济的影响。结果显示，在区制1（风险水平低）的情况下，持续处于危险状态的概率为0.918；而在区制2（风险水平高）的情况下，保持在高风险状态的概率为0.625。此外，高风险区主要集中在2008年次贷危机后，尤其是2013年之后，金融风险频繁发生，这会对我国宏观经济的恢复能力、人们的预期以及经济运行情况产生一定影响，进而导致宏观经济波动加大。而在区制1的滞后1期，SFRI对当期SFRI有显著的正向影响，影响系数为0.479，在1%置信水平下显著；MCI对当期同样具有显著的正向影响，影响系数为1.702；滞后2 期和滞后3 期时为显著的负向影响，影响系数分别是-0.655和-0.308。在区制2状态下，无论是滞后1期还是滞后3期的SFRI对当期自身都具有正向显著影响，影响系数分别是0.925和0.760；滞后1期和滞后4期的MR对当期的影响系数分别是0.641 和0.701。上述结果表明，这两个不同的区域体系在没有重大外部影响的情况下会保持相对稳定的状态，而经济景气因素在短期内可能通过正向反馈机制进行自我强化，但在中长期则可能存在反向调节；此外SFRI、MR和MCI在高风险水平下仍然具有一定的惯性。综合研究结果来看，系统性金融风险对宏观经济具有时变的特征。在短期内，它对宏观经济造成负向冲击，但及时采取预防和控制措施，并通过政策引导和市场自发调整，有序处置突出风险，可以提高经济的韧性，促进经济向高质量发展迈进。总体来讲，研究通过运用CRITIC法和因子分析法，构建系统性金融风险指数，以此定性和定量地评估我国系统性金融风险的水平。另外研究还将经济韧性这一指标加入对宏观经济抵御风险和冲击的评价中，为宏观经济的发展提供了一个新的研究视角。而通过对系统性金融风险和宏观经济的关系进行分析，不仅为如何提高经济的风险抵抗能力提供了思路，还为促进经济健康和高质量发展提供了有力指导。