基于模型不确定性自适应估计的工业机械臂改进TDE控制策略*

高舒芳,张 文,吴 凯

(1.山西工程科技职业大学 智能制造学院,山西 晋中 030619;2.太原理工大学 机械与运载工程学院,山西 太原 030024;3.合肥通用机械研究院有限公司,安徽 合肥 230031)

0 引 言

工业机械臂是数智化时代先进制造业中的关键执行单元,其被广泛应用于汽车零部件制造[1-2]、高精密电子元器件制造[3]、光学元件精密制造[4]等领域。对机械臂进行高精度、强鲁棒性的运动控制是工业机械臂有效服役的关键前提。

工业机械臂动力学包含了重力、科氏力、离心力、摩擦力和其他干扰项,是一种高度非线性系统,因此,机械臂的精确运动控制难度极大。过去几十年来,国内外学者广泛开展了基于模型的机械臂运动控制方法研究[5-8],取得了良好的效果。然而,由于识别机械臂动力学参数存在很大难度,且模型参数的数量随着机械臂自由度的增大而显著增加,因而大多数基于模型的机械臂运动控制器都非常复杂,且对参数变化非常敏感。

为避免上述控制方法(基于模型控制)的缺陷,近年来国内外学者广泛研究了智能化的无模型机械臂控制方法[9]。

VO A T等人[10]设计了固定时间滑模控制律,同时结合径向基神经网络,估计了机械臂动力学特性的不确定项,其可以有效控制抖振现象的产生。DENG Fu-wei等人[11]引入了无模型控制思想,建立了机械臂动力学超局部模型,并利用时延估计逼近超局部模型中的未知项,最后设计了改进的滑模控制律,在完成精确位姿控制的同时减小了控制器抖振。王建平等人[12]提出了一种基于深度强化学习的机械臂运动控制方法,进行了二连杆机械臂无模型数据驱动控制,该方法具有高效、适应性强的优点。

基于时延估计的控制(time-delayestimation-basedcontrol,TDEC/TDC)是一种能够对存在外部扰动和模型不确定性的非线性复杂系统进行有效控制的无模型方法,其具有简单、高效和强鲁棒性的优点,被广泛应用于工业机械臂控制领域[13-16]。TDEC方法基于样本延迟信息对未知的动力学参数和模型不确定性进行建模和消减。实际应用证明,被控系统越复杂、不确定程度越高,TDEC方法的控制效果越显著[17]。

然而,当系统摩擦力、有效载荷或轨迹等存在突变时,采用TDEC会存在较大估计误差(即“TDE误差”),因此,许多学者将辅助控制器集成到TDE控制器中,开展了广泛的研究。

LEE J等人[18]提出了一种基于自适应积分滑模控制和TDE的鲁棒控制器,采用TDE来估计具有参数变化和干扰等不确定性的机械臂动力学响应,并采用积分滑移面替代了传统滑模控制中的到达相位和噪声敏感切换动作,控制效果鲁棒性较强。KIM J等人[19]基于TDE方法设计了模糊PID控制器,并证明了在离散时域内,所提出的模糊PID控制器是TDE控制器的扩展集,最后利用PUMA型机械臂验证了该控制器的有效性。WANG Yao-yao等人[20]将TDE与分数阶非奇异终端滑模控制相结合,提出了一种新的非线性自适应控制律,其具有稳定性高、控制精度好的优势。

但是,现有的多数方法采用了传统的TDEC技术,因此,控制效果在很大程度上依然受到TDEC方法的限制,无法较好地平衡TDE误差和控制输入抖振现象,尤其是当系统受到间歇性扰动或存在较大不确定性时,已有基于TDEC方法的控制策略容易出现严重问题。文献[21]、[22]试图通过在每个采样点寻找适当的TDEC控制增益来解决上述问题,但控制效果的不确定性依然较大。

基于TDEC方法的上述缺陷,笔者提出一种改进的TDEC方法,即将模型不确定性自适应估计器集成到经典TDEC中,并融合滑模控制,形成完整的多级控制策略框架,对机械臂输入扭矩进行鲁棒控制;利用Lyapunov方法对改进的TDEC控制策略的稳定性进行证明;最后,通过仿真分析和实验的方式,以此来验证该控制策略的有效性和优越性。

1 多自由度机械臂TDEC方法

1.1 多自由度机械臂动力学模型

具有n自由度的机械臂动力学方程可表示为:

(1)

(2)

上述动力学系统式(1)满足如下性质和假设[24]。

(3)

式中:‖·‖为矩阵诱导范数运算符。

(4)

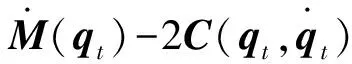
(5)

式中:Fc为库伦摩擦系数;Fv为黏滞摩擦系数;sgn(·)为符号函数。

1.2 机械臂TDEC方法基础

(6)

式中:Nt为集总不确定性扰动项,表示为:

(7)

为消去式(6)中的Nt,将控制输入力矩表示为:

(8)

上述误差控制项ut如下所示:

(9)

式中:qd,t为机械臂关节参考轨迹(转角)向量;et为轨迹跟踪误差向量;Kd,Kp为常系数对角阵,Kd=diag(kd,11,…,kd,nn),Kp=diag(kp,11,…,kp,nn)。

(10)

式中:L为采样周期。

将式(8)和式(10)代入式(6),得到:

(11)

对于TDE误差Γt,当其满足下式的稳定性条件[16]1711-1712时,有Γt<Γ*(Γ*为常向量),此时跟踪误差et收敛,公式如下:

(12)

式中:I为单位矩阵。

由此可见,基于TDE的控制方法总是存在TDE误差与抖振之间的权衡。

基于TDE控制方法的权衡曲线示意图如图1所示。

图1 基于TDE控制方法的权衡曲线示意图

由图1可知:由于采用了固定的控制增益,经典TDEC的控制效果为权衡曲线上的固定点;而自适应TDEC(adaptive time-delay estimation based control,ATDEC)的控制效果动态权衡TDE误差和控制输入抖振之间的相对值。

因此,笔者的目的是在已有方法的基础上,通过引入模型不确定性自适应估计,同步降低TDE误差和控制输入抖振,从而实现更为优良的基于TDEC的机械臂轨迹控制目的。

2 模型不确定性自适应估计方法

对工业机械臂进行控制的目标是使其关节实际轨迹能够精确跟踪期望的参考轨迹。

为设计一种能够有效减小跟踪误差的自适应控制方法,笔者引入了滑动变量。对于滑动变量st∈Rn,采用如下线性滑模面:

(13)

式中:Λ为正定对角阵,Λ=diag(Λ11,Λ22,…,Λnn),Λ决定了跟踪误差在滑模流形上收敛于0的速度。

2.1 模型不确定性自适应估计器设计

参考式(10),针对Nt设计了如下基于延迟信号及其梯度的自适应估计模型:

(14)

式中:Wt为梯度效应调节系数矩阵,Wt=diag(W11,t,…,Wnn,t)∈Rn×n。

基于引入的滑模变量,Wt的元素由如下公式进行自适应计算:

(15)

综合式(8)、式(13)及式(14),给出如下输入力矩的控制律:

(16)

式中:Ks为开关增益矩阵,且Ks=diag(ks,11,…,ks,nn)。

将式(16)代入式(6),得到如下所示的误差动力学方程:

(17)

与经典的TDEC相同,该控制方案的第一辅助控制器起到了稳定名义模型式(6)的作用,而第二辅助控制器则起到进一步抑制残余误差、稳定控制效果的作用。

此外,因为TDE控制器相互独立,所以模型不确定性自适应估计器能够进一步集成到自适应TDEC方法中,形成更为有效的控制策略。

最后,虽然改进的TDEC控制方法依然在TDE误差与控制输入抖振现象之间进行权衡,但权衡曲线相较于基于经典TDEC方法更低。

改进的TDEC控制算法整体结构如图2所示。

图2 改进的TDEC控制算法整体结构

2.2 稳定性分析

笔者为说明改进的TDEC控制方法的稳定性,考虑如下的Lyapunov函数:

(18)

对上式取时间导数,并将式(17)代入,可得出:

(19)

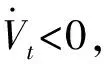
首先,根据式(9)和式(11),TDE误差Γt可以改写为:

(20)

根据文献[25]中的方法,关于Γt的闭环动力学方程可表示为:

(21)

其中:

(22)

因此,当时延L足够小时,上述η1,t和η2,t为有界量。结合条件式(12),可以得出TDE误差Γt有界。

(23)

因此,可以得出:

(24)

由上述过程可以看出,TDE误差Γt以及Wii,t均有界,此时有:

W+·Γ*

(25)

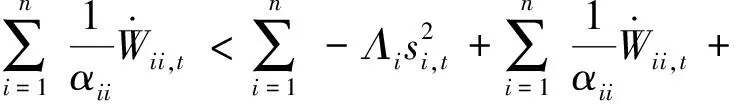
(26)

将开关增益ks,ii设置为:

(27)

则有:

(28)

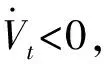
(29)

综上,对于非零si,t,Lyapunov函数的时间导数总为负。因此,当式(12)和式(27)成立时,可以保证闭环系统在滑模面st=0上渐近稳定。此外,算法的调节参数γii决定了Lyapunov函数的收敛速度。

2.3 参数调节策略

针对改进的TDEC控制方法,笔者设计了如下的参数调节策略:

步骤1。确定第一辅助控制器中的Λ,使下述特征方程具有所期望的极点:

(30)

值得注意的是,根据标准的二阶系统理论,可以选择式(30)中的两个极点,以获得理想的上升时间、调节时间、超调量等;

步骤4。选择式(16)中第二辅助控制器的ks,ii。由于ks,ii的取值同时影响跟踪性能和抖振效应,而自适应时延估计在一定程度上保证了跟踪性能,因此,可以选择较小的ks,ii值以避免抖振。

3 仿真分析

笔者采用简化版三连杆PUMA型机械臂[26]进行了仿真分析。

仿真机械臂构型及其参数如图3所示。

图3 仿真机械臂构型及其参数

仿真机械臂动力学参数如表1所示。

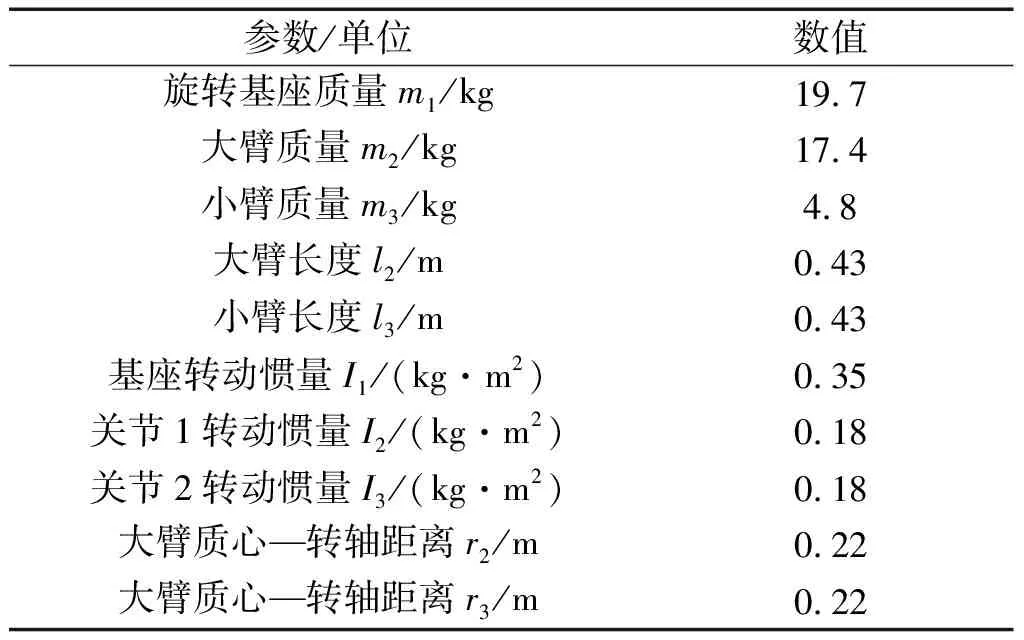
表1 仿真机械臂动力学参数

仿真案例中给定的参考关节轨迹为qd,t=[sin(t),cos(t),0.8·sin(t)],采样周期L为1 ms,仿真时间为30 s。

仿真分析在如下两类条件下开展:

1)变频条件。为证明改进的TDEC算法的有效性,令参考轨迹频率在12 s后增大为原值的二倍;

2)变载荷条件。利用前述变频条件下的参考轨迹,在10 s～12 s之间对机械臂施加5 kg载荷。

为定量评价控制性能和抖振,笔者计算了跟踪误差的均方根值(root mean square value of error,RMSE)和测量能耗的平方值积分(integral square value,ISV)。其中ISV的计算公式为:

(31)

式中:T为计算时间。

为节省篇幅,此处笔者仅针对末端关节的跟踪误差和抖振情况进行分析。

各方法对于末端关节控制的跟踪误差对比曲线如图4所示。

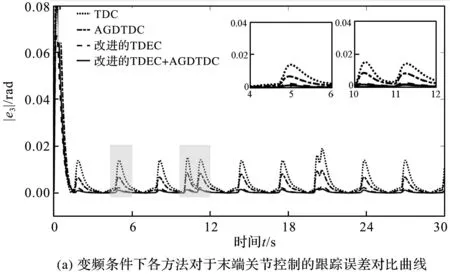
图4 各方法对于末端关节控制的跟踪误差对比曲线

仿真分析中,各方法的RMSE和ISV定量对比结果(RMSE/ISV)如表2所示。

表2 仿真分析中各方法的RMSE和ISV定量对比结果(RMSE/ISV)

由图4及表2可以看出:改进的TDEC算法不仅优于经典的TDEC方法,而且控制输入抖振也显著降低。同时,即使参考轨迹变化频率或有效载荷发生变化,在不失鲁棒性的情况下,改进的TDEC算法依然可以获得较小的跟踪误差。此外,与AGDTDC方法相比,集成了模型不确定性自适应估计器的改进AGDTDC获得了更好的轨迹控制效果。因此,改进的TDEC算法具有良好的灵活性。

然而,改进的AGDTDC的输入抖振较高,这是因为AGDTDC在提高控制精度与抑制输入抖振的权衡中选择了前者。

4 实验验证

为了进一步验证改进的TDEC算法的实用性,笔者采用六自由度Indy-7机械臂进行了实验[29]。

机械臂质量为28 kg,其中关节1～3的电机齿轮比为1∶121,关节4～6的电机齿轮比为1∶101,角度测量采用16位编码器,重复性为100 μm。

在不失一般性条件下,实验过程仅针对关节1～3进行控制。为了施加扭矩,第一、第二轴和第三关节分别使用了两台PUCK驱动器,驱动器可产生的额定扭矩分别为117.73 N·m和47.5 N·m,最大峰值扭矩分别为431.97 N·m和193.27 N·m。采样周期L为0.25 ms。控制算法在Ubuntu 12.04上采用C++编写,计算出的信号通过CAN总线传输到采用转矩模式控制的PUCK驱动器中。同时,实验在加载/零载两种条件下进行,实验时间为30 s。

实验采用的机械臂控制系统框图如图5所示。

图5 实验采用的机械臂控制系统框图

Indy-7机械臂的结构及关节期望轨迹如图6所示。

在未施加有效载荷的条件下,改进的TDEC方法与经典TDC的控制效果对比如图7所示。

图7 未施加有效载荷的条件下改进的TDEC方法与经典TDEC的控制效果对比

在施加有效载荷条件下,各方法的控制效果对比(以关节1为例)如图8所示。

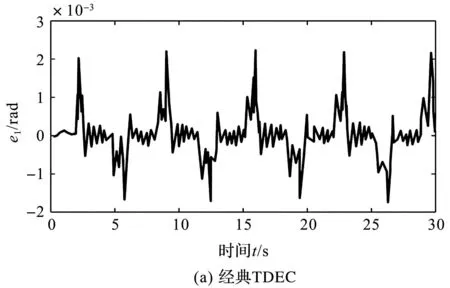
图8 施加有效载荷下各方法的控制效果对比(以关节1为例)

实验中各方法控制误差RMSE(未加载/加载)定量对比结果如表3所示。

表3 实验中各方法控制误差RMSE(未加载/加载)定量对比结果

实验中各方法控制过程中(未加载/加载)测量计算的ISV定量对比结果如表4所示。

表4 实验中各方法控制过程中(未加载/加载)测量计算的ISV定量对比结果

由图7、表3及表4可以看出:在未对机械臂施加有效载荷的条件下,改进的TDEC方法的轨迹控制性能优于经典的TDEC及AGDTDC方法;通过对TDEC方法分别与TDC、AGDTDC两种方法的数据对比分析,分别计算了三个关节轨迹控制精度提升的百分比,再求三个百分比的平均值,改进TDEC方法相较于经典TDEC、AGDTDC两种方法对于三个关节的轨迹控制精度平均分别提升了45.38%及36.40%。这是由于改进的TDEC方法在经典TDEC方法基础上完成了更有效的模型不确定性估计任务。同时,与已有AGDTDC方法相比,改进的AGDTDC方法的轨迹控制性能更为优良,且输入抖振抑制效果也有所提升,说明了改进的TDEC模型不确定性自适应估计器的灵活性与有效性[30-31]。

5 结束语

笔者提出了一种基于模型不确定性自适应估计的改进TDEC方法,并利用Lyapunov理论分析了该控制策略的稳定性,最后通过仿真分析和实验验证了改进的TDEC方法的有效性和优越性。

结论如下:

1)模型不确定性自适应估计器充分考虑了机械臂动力学模型扰动项的时延估计值及其梯度,将其与TDE控制器结合,能够有效提升控制精度并减少控制输入抖振现象。实验结果表明,在相应降低控制输入抖振程度的同时,在机械臂三个关节未加载/加载的条件下,相较于经典TDEC方法,改进的TDEC控制策略的控制精度平均分别提高了45.38%及62.29%;相较于AGDTDC方法,该控制策略的控制精度平均分别提高了36.40%及23.31%;

2)基于TDE的控制方法均不可避免地需要在控制精度与输入抖振现象间进行平衡;相较于经典TDEC以及已有的AGDTDC方法,改进的TDEC控制方法的平衡曲线更低;

3)改进的TDEC模型不确定性自适应估计器与TDE控制器相对独立,能够有效地与已有自适应TDC方法相结合,并取得更为良好的控制效果。

在后续研究中,笔者将围绕改进的TDEC模型不确定性自适应估计方法与其他控制技术相结合,为高度不连续、非线性系统提供更为有效的控制方案。