面向类不均衡数据的多任务博弈概率分类向量机*

潘海洋,李丙新,郑近德,童靳于

(安徽工业大学 机械工程学院,安徽 马鞍山 243032)

0 引 言

滚动轴承作为机械设备不可或缺的组成部分之一,被广泛应用于工业领域中。由于很多滚动轴承处于高速、重载等复杂工况下,致使其成为最易发生故障的零件之一。根据CERRADA M等人的统计,滚动轴承故障在旋转机械总故障中占比40%左右[1-3]。因此,开展滚动轴承状态监测与诊断对提高机械设备的可靠性与安全性具有重要意义。

近年来,基于数据驱动的智能故障诊断方法在滚动轴承故障诊断中得到广泛应用[4-5],如人工神经网络(artificial neural network,ANN)算法、支持向量机(support vector machine,SVM)、相关向量机(relevance vector machine,RVM)等方法。人工神经网络是一种基于人体大脑神经的复杂网络系统,拥有较强的容错性和判断能力,被广泛应用于故障诊断领域。但是,ANN及其改进算法基于经验风险最小化建立优化目标,容易陷入局部最优。SVM不同于神经网络算法,其基于结构风险最小化原则,通过求解凸优化问题可以获得全局唯一解,从而解决了局部最优问题[6]。

由于SVM具有优越的分类能力,相关学者提出了多种SVM演生算法,如,LI Yan-meng等人[7]提出了一种孪生支持向量机(twin support vector machine,TWSVM)方法,其通过构造一对非平行超平面,解决了SVM中计算复杂度过高的问题;但处理大规模数据集时,TWSVM存在耗时的问题。CHEN Su-gen等人[8]提出了一种基于最小二乘支持向量机的故障诊断模型,其采用免疫算法克服了易陷入局部最优的不足;但其对离群点仍较为敏感,导致模型泛化性能下降。此外,SVM及其改进算法易受Mercer定理的限制,且预测结果缺少后验概率,使其不具统计意义,制约着算法的进一步发展。

在理想情况下,研究者通常希望模型能够用于估计条件分布,以更好地捕捉预测中的不确定性。但是,SVM提供的是“硬”的二元决策,只能给出明确的分类结果,难以利用结果观测获得分类的理想准确度[9-11]。基于此,相关学者提出了一种基于贝叶斯理论的统计学分类算法,即相关向量机[12]。RVM既可以实现概率性预测,也不受制于Mercer定理,且稀疏性和泛化能力明显优于SVM;但RVM仍存在一些不足[13],如大量样本下训练时间过长,使得模型训练学习速度下降;噪声对模型构建造成影响,降低分类精度,使得模型鲁棒性变差;使用单一核函数对全部数据进行映射时存在局限性等。

为了解决上述问题,YANG Zheng-rong[14]提出了一种快速训练方法,其采用Gram-Schmidt算法剔除一些依赖性点以减少训练样本的数量,解决了RVM在大规模训练集上训练时间过长的问题;但易受数据集影响而导致分类性能下降。王波等人[15]提出了一种基于多核多分类相关向量机的多特征融合智能故障诊断方法,其采用加权求和融合多种特征信息的方法,解决了不同特征直接融合导致的维数增高的问题;但其迭代运行时间较长,时效性有待提高。此外,RVM及其改进算法仍存在使用零均值高斯分布导致基样本不可靠的问题,增加了模型的不稳定性[16]。针对上述问题,CHEN Huan-huan等人[17]进一步提出了概率分类向量机(probabilistic classification vector machine,PCVM),采用了截断高斯先验方法,不仅使得样本参数的正负与对应的标签信息相同,而且使权重向量产生稀疏估计,降低了模型的复杂性。因此,相比于SVM和RVM,PCVM的输出结果不仅具有概率统计意义,而且还具有稀疏性和稳定性;但面对数据不平衡分类问题时,PCVM的分类性能表现欠佳。

工程实际中,机器运行大多处于正常工作状态,故障样本的获取极为困难,呈现出不均衡特点。由于SVM、RVM和PCVM方法在建模时没有考虑类不均衡分类问题,致使其建立的模型出现偏向性,即分类倾向于多数类样本[18-20]。

针对上述问题,基于稀疏贝叶斯理论、模糊隶属度等理论,笔者提出一种MGPCVM模型。

通过在目标函数中构建博弈约束项,基于样本质心和样本不平衡比等信息,给出一系列不同样本质心敏感值,使不同类别的样本点具有不同的样本质心敏感值;并利用两个不同的滚动轴承故障数据集进行实验分析,最后对MGPCVM方法的故障诊断分类性能进行验证。

1 多任务博弈概率分类向量机

MGPCVM是一种基于稀疏贝叶斯理论的核函数学习方法,其通过引入截断高斯先验、模糊隶属理论等使模型实现稀疏性,并为不同类样本点赋予不同的样本质心敏感值,消除了数据不平衡对模型构建造成的影响。

(1)

式中:Φθ(x)为基函数(核函数)向量,表达式为Φθ(x)=(φ1,θ(x),…,φN,θ(x));ω为模型权重向量,ω=(ω1,…,ωi)T,每个元素ωi均服从截断高斯先验;b为偏置,服从零均值高斯先验。表达式如下:

(2)

对上式进一步化简可得:

(3)

式中:α为截断高斯分布的逆方差;β为标准高斯分布的逆方差。

笔者采用高斯核函数作为基函数,其一般形式表示如下:

(4)

式中:θ为基函数(核函数)的参数。

为了使数值输出转化为概率输出,MGPCVM使用了标准高斯累积分布函数作为概率链接函数,将实数映射到[0,1]之间。其公式表示如下:

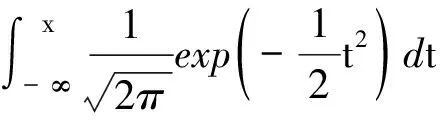
(5)

在概率模型中,笔者在稀疏预测模型Φθ(x)ω+b附加一个噪声ξ～N(0,1),以增强模型鲁棒性。模型hθ=Φθ(x)ω+b+ξ≥0时,样本属于正类的概率大于样本属于负类的概率,即样本属于正类的概率大于0.5;若hθ<0,则样本属于负类的概率大于0.5。由于ξ为一个观测不到的变量,故hθ为隐变量。

关于Hθ的似然函数表示如下:

p(Hθ|ω,b)=

(6)

式中:I为元素全为1的N维向量;sn为样本质心敏感值;sn(Hθ-(Φθω+bI))为博弈约束项。

其中:Φθ(xi)=(φθ(x1,xi),…,φθ(xN,xi)),Φθ=(Φθ(x1)T,…,Φθ(xN)T)T,Hθ=(hθ(x1),…,hθ(xN))T。

(7)

式中:IR为负类样本数与正类样本数的比值,表示不平衡比;d1为样本点与正类(少数类)样本质心的欧氏距离;d2为样本点与负类(多数类)样本质心的欧氏距离;d为两类样本质心之间的欧氏距离;r2为负类样本与其同类样本质心之间的最大距离;C0为一个常数,决定了指数函数的尺度。

由式(7)可以看出:根据负类样本点相对于两类样本质心的位置,负类样本质心敏感值取值范围为1/(1+IR)到1,大小与IR有关;当d2=0时,负类样本质心敏感值等于1,这使得d1=d;当样本点最接近正类样本质心时,即d1=0,导致d=r2,且离负类样本质心最远时,即d2=r2,负类数据点的样本质心敏感值等于1/(1+IR)。

为了获得完整的后验分布,将α和β视为隐变量,此时存在hθ,α,β三个隐变量,则参数ω和b的后验分布表达式表示如下:

(8)

取后验分布的对数形式,公式表示如下:

logp(ω,b|y,Hθ,α,β)∝logp(Hθ|ω,b)+

logp(ω|α)+logp(b|β)∝-[sn(Hθ-(Φθω+

bI))]2-ωTAω-βb2

(9)

式中:A为对角矩阵,A=diag(α1,…,αN)。

为了求解参数ω和b的极大后验估计,笔者采用期望最大化算法求解参数ω和b的后验概率估计,并在此过程中使用共轭梯度法获得最优θ值。

因此,得到Q函数表示如下:

Q(ω,b|ωold,bold)=EHθ,α,β[logp(ω,b|y,Hθ,α,β)|y,

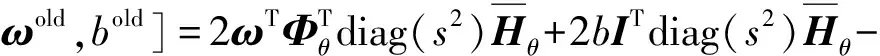
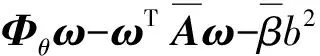
(10)

进一步获得Q函数的偏导,表示如下:

(11)

(12)

(13)

式中:⊙为元素的哈达玛矩阵乘法符号,表示矩阵对应位置的元素相乘。

令式(11)和式(12)等于0,求解得到的ω和b更新式表示如下:

(14)

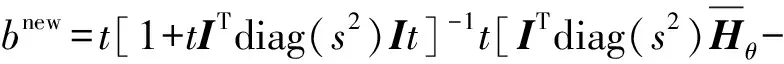
ITdiag(s2)Φθω]

(15)

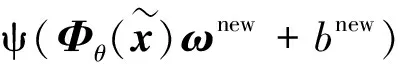
(16)

2 MGPCVM方法分类流程

为验证MGPCVM方法的有效性,笔者将滚动轴承故障振动信号作为具体的研究对象。

MGPCVM方法分类流程图如图1所示。

图1 MGPCVM方法分类流程图

诊断过程可以分为以下几个环节:

1)滚动轴承振动信号由传感器进行测量,并由数据采集系统进行采集;

2)对数据进行特征提取后,随机分为训练样本和测试样本;

3)对训练样本采用“一对一”策略完成多分类模型的构建,然后利用测试样本验证模型准确性,并给出诊断结果。

3 实验与结果分析

笔者采用两种不同的实验台获得实验数据:1)湖南大学锥齿轮-滚动轴承实验平台数据集;2)安徽工业大学滚动轴承故障模拟实验台数据。

笔者在滚动轴承正常、内圈故障、外圈故障和保持架故障(滚动体故障)4种类型中选取6种不同状态进行实验验证。

两种实验台的滚动轴承数据信息如表1所示。

表1 滚动轴承数据信息

3.1 湖南大学轴承故障实验

为了验证MGPCVM方法的优越性,笔者首先采用湖南大学滚动轴承故障实验数据集进行验证。

湖南大学锥齿轮-滚动轴承实验台如图2所示。

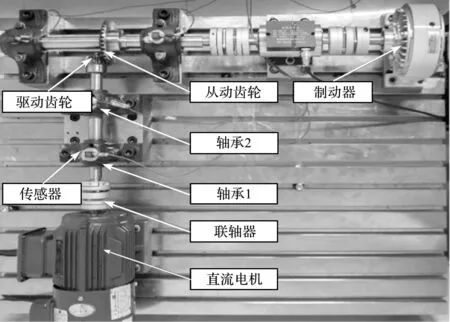
图2 湖南大学锥齿轮-滚动轴承实验台

湖南大学滚动轴承数据集如表2所示。

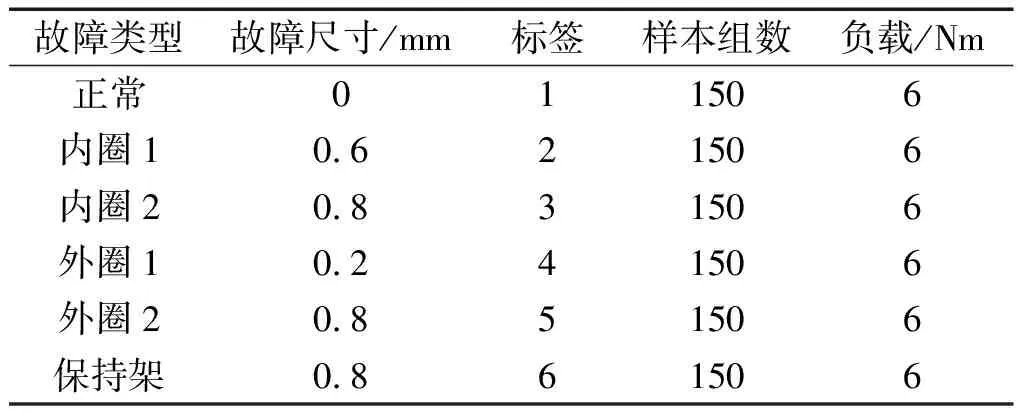
表2 湖南大学滚动轴承数据集

滚动轴承每种运行状态有150组数据,笔者将数据按2∶1划分为训练集和测试集。

为避免诊断结果的偶然性,笔者采取随机选取训练集的策略,在每种故障类型的150组样本中,随机抽取100组样本作为训练集,50组样本作为测试集。

湖南大学轴承数据IR设置如表3所示。

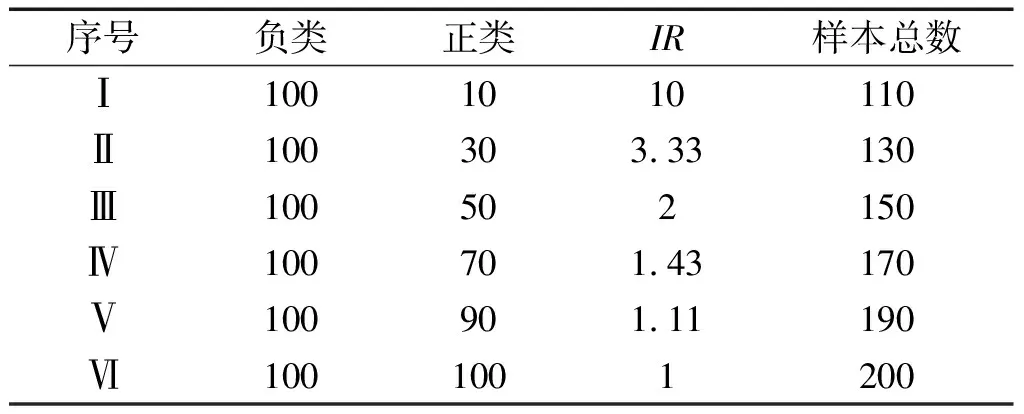
表3 湖南大学轴承数据IR设置

为了客观评价MGPCVM方法的性能,笔者将MGPCVM与SVM、TWSVM和PCVM进行了对比,并选择准确率、F1-score、Kappa、Precision、Recall等评价指标来综合评价模型的分类性能。在不同IR下进行5次实验,并取平均值。

4种分类方法在不同评价指标下的对比如图3所示。

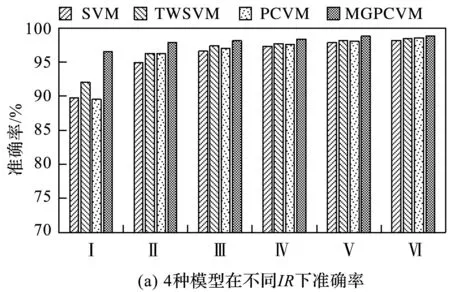
图3 4种分类方法在不同评价指标下的对比

从图3(a)～图3(e)可以看出:在5个模型评价指标下,IR值较大时,SVM、TWSVM和PCVM均未达到理想效果,而在样本失衡时,MGPCVM仍具有较高的识别率。在不同IR实验条件下,MGPCVM方法的分类性能均表现最好,优于其他对比方法。其中,不平衡比最大时,即IR为10时,MGPCVM相较其他方法的效果最为显著,MGPCVM平均分类准确率达到96.534%,而SVM、TWSVM和PCVM分类准确率为89.800%、92.066%和89.532%,分别提升了6.734%、4.468%和7.002%。随着IR的降低,即类间平衡度提高,总体呈现上升趋势,且4种分类方法分类性能的差距逐渐减小。

产生上述结果的原因在于:MGPCVM模型考虑到了每个样本对样本质心的敏感度,并使用基于距离的博弈约束项,对样本赋予不同的样本质心敏感值,少数类样本敏感值为1,而多数类样本综合考虑其与同类样本质心的距离以及异类样本质心的距离,然后赋予不同的敏感值,进而能够考虑并改善不平衡样本对分类模型构建产生的影响。SVM、TWSVM和PCVM三种方法默认对所有样本设置为1的敏感值,并未考虑到样本的数量和距离等因素,使分类器的性能更偏向于多数类,降低了分类效果。

因此,实验结果表明,该MGPCVM方法在样本不均衡条件下的效果更加明显。

3.2 安徽工业大学轴承故障模拟实验

为了再次验证MGPCVM方法的有效性,笔者拟选择安徽工业大学滚动轴承故障模拟实验数据进行实验。

安徽工业大学滚动轴承故障模拟实验台如图4所示。

图4 安徽工业大学滚动轴承故障模拟实验台

安徽工业大学滚动轴承数据集描述如表4所示。

表4 安徽工业大学滚动轴承数据集描述

在每种故障类型的150组实验数据样本中,笔者随机抽取100组样本作为训练集,50组样本作为测试集。

安徽工业大学轴承数据IR设置如表5所示。

表5 安徽工业大学轴承数据IR设置

SVM、TWSVM、PCVM和MGPCVM 4种方法在不同IR下分类准确率如图5所示。

图5 4种方法在不同IR分类准确率

从图5可以明显看出:在不同的IR下,MGPCVM方法分类准确率保持在95%以上。当IR=10时,MGPCVM方法效果最为明显,随着IR降低,4种分类方法的准确率均呈现上升趋势,且4种方法的准确率值之差逐渐缩小。

为了对MGPCVM方法进行综合评价,笔者仍选择准确率、F1-score、Kappa、Precision、Recall等评价指标评价的分类性能。

4种方法对比结果如表6所示。

表6列出了4种分类器在不同评价标准下的对比结果。

由表6可以看出:当IR=10时,MGPCVM平均分类准确率为95.868%,SVM、TWSVM和PCVM分类准确率为90.800%、91.800%和89.534%,分别提升了5.068%、4.068%和6.334%。

在F1-score、Kappa、Precision、Recall等评价指标下,PCVM的分类性能在4种方法中的表现最差,面对不平衡数据分类时,PCVM难以建立具有平衡性的预测模型,进而制约着分类性能;SVM的表现次之,其最优超平面更加偏向于少数类,使得分类结果表现一般;TWSVM方法构造了两个非平行的超平面,其优化问题是使每个超平面更接近自己的类别而远离另一个类别,故处理不平衡数据时,分类性能要优于SVM,但忽略了不平衡样本质心敏感值;MGPCVM模型综合考虑样本质心距离和不平衡比等信息,赋予不同样本以不同的样本质心敏感值,故分类表现理想且均为最优。

综上所述,在不同指标下,SVM、TWSVM、PCVM和MGPCVM的准确识别率均呈现上升趋势,并且MGPCVM在不同的IR下表现最好,显著优于其他三种对比方法。

因此,通过以上两个实验分析,分析结果证明了MGPCVM分类方法的可行性和优越性。

4 结束语

针对传统分类模型对不平衡样本数据分类难以达到理想效果的问题,笔者提出了MGPCVM模型,通过设计样本质心博弈约束项,综合考虑了样本点距离及不平衡度等信息;为了验证MGPCVM模型的有效性,针对湖南大学和安徽工业大学两个轴承实验台数据进行了实验。

研究结论如下:

1)MGPCVM模型通过赋予各类样本不同的样本质心敏感值,充分利用样本间质心博弈信息,解决了传统分类器针对不平衡数据集较弱的问题;

2)在贝叶斯推理过程中使用截断高斯先验,不仅可以获得概率输出结果,同时确保了样本参数正负与标签保持一致,且使样本质心敏感值具备了稀疏性;

3)通过两种实验台的滚动轴承故障数据实验分析,在F1-score、Kappa、Precision、Recall等评价指标下,MGPCVM方法分类性能保持在95%～99%,优于SVM、TWSVM和PCVM分类方法,有效地提高了非平衡数据分类精度。

然而,该模型存在训练较长等不足之处,在后续的研究方向中,笔者将针对该模型的时间成本等问题进行研究,进一步提升分类模型的效率。