基于有限时间观测器的光储系统母线电压互补滑模控制

皇金锋 杨振宇

（陕西理工大学 电气工程学院，陕西 汉中 723001）

随着能源危机与环境问题的日益凸显，可再生能源的发展越来越受重视.直流微电网［1］作为一种高效的能源利用措施，因其结构简单、控制方便、效率高等优点，在各行业中的应用越来越广泛.其中采用太阳能发电的光伏微网［2］，减少了对传统能源的依赖，具有节能环保的优点.但由于太阳能资源的随机性，系统运行常受到电压质量问题的影响.因此，有必要接入储能装置［3-4］，补偿光伏间歇性的功率波动，增强光伏直流微网系统运行的稳定性.蓄电池和超级电容分别作为高能量密度和高功率密度的储能元件，具有互补的工作特性，构成的混合储能系统（Hybrid Energy Storage System，HESS）在光储直流微网［5-6］中得到了广泛应用.

光储直流微网不需要考虑无功，只有有功功率，母线电压［7-8］作为反映功率平衡的唯一标准，成为当前的研究热点.直流微电网运行中常受到能源间歇性输入、负载随机性扰动以及功率流向切换等干扰，这些干扰都会对母线电压的稳定运行产生影响.为提高母线电压运行的稳定性，研究人员提出了多种非线性控制策略，如微分平坦控制［9］、自抗扰控制［10-11］、滑模控制等.其中滑模控制因其鲁棒性强，响应速度快，对系统扰动、参数摄动具有完全的自适应性等优点，在非线性系统控制中取得了良好的控制效果，如四旋翼无人机［12］，永磁同步电机［13］，机械臂［14］等.但滑模控制本身存在抖振问题，成为实际应用中的主要障碍.为优化滑模控制器参数，提升系统控制性能，有学者提出将滑模控制与人工智能结合的思想.杨旭红等［15］针对Vienna 整流器对参数扰动敏感，抗干扰能力差等问题，提出将神经网络与滑模控制相结合的策略，改善了系统的动静态性能.金鸿雁 等［16］将互补滑模（Complementary Sliding Mode Control，CSMC）与迭代学习控制相结合，提高了永磁同步电机［17］的控制性能.

裴斯诺等［18］针对传统PI 控制下，储能变流器跟踪滞后以及抖振幅度大的问题，提出一种超螺旋滑模控制，提高了变流器的响应速度和鲁棒性，但由于电网运行情况复杂，微源以及负荷的扰动会造成系统抗扰性能变差.张世欣等［19］针对自抗扰控制中的PD 控制鲁棒性差的问题，设计改进型滑模自抗扰控制，提升了直流微网系统的稳定性.董锋斌等［20］针对双馈风力发电机运行中的不确定性，引入扩张状态观测器（Expanded State Observer，ESO），通过估计系统总扰动并采用滑模控制进行补偿，减小抖振的同时也提高了系统抗干扰能力.但普通ESO 的观测能力有限，只能达到渐进收敛.为了提高观测器的收敛性能，沙磊等［21］为二质量系统设计了有限时间滑模控制策略，提高了系统的跟踪性能以及抗扰能力.

本文针对受外界扰动、不确定性影响的光储直流微网混合储能系统，提出一种基于有限时间观测器的互补滑模控制.通过设计有限时间扩张状态观测器来估计系统总扰动，实现系统全局有限时间稳定，并将总扰动输入到控制端进行补偿，设计互补滑模控制器，提高系统的控制性能，并通过仿真验证了本文所提控制方法的有效性.

1 光储直流微网系统

1.1 系统结构

本文采用的光储直流微网系统如图1 所示.该系统包括光伏（PV）、超级电容（SC）、蓄电池（Bat）、直流负载、直流母线和相连接的变换器.光伏电源处于放电状态，向直流母线提供能量，并输出功率.直流负载是电源终端，吸收功率.蓄电池和超级电容形成HESS，通过双向变换器吸收或释放能量，抑制可再生能源的波动性和间歇性，提高系统的稳定性.

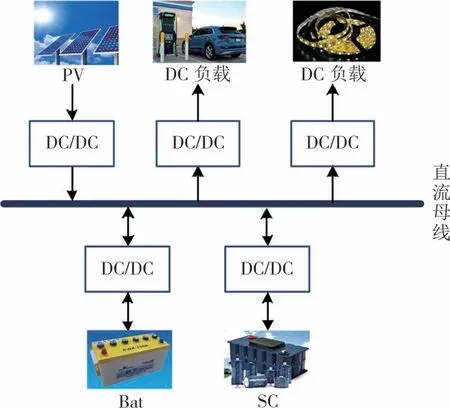
图1 光储直流微网系统结构图Fig.1 Structure diagram of optical storage DC microgrid system

1.2 功率分配

在光储直流微电网中，各单元间的关系如下.

式中，PPV是光伏提供的功率；PES是HESS 提供的功率；PL是负载所需的功率.

混合储能系统的功率关系为

式中，Pbat是Bat提供的功率；Psc是SC提供的功率.

因蓄电池和超级电容是并联接线，当不考虑线路阻抗时，功率分配可等效为电流分配.其电流分配关系为：

式中，Iref为总输出电流参考值；Ibat为蓄电池输出电流；Isc为超级电容输出电流.

根据超级电容快速性的特点，通过总输出电流Iref减去超级电容实际电流Isc，可得到蓄电池参考电流Ibatref为

将未补偿的蓄电池电流添加到超级电容电流参考值中，从而得到超级电容参考电流Iscref为

式中，YLPF为低通滤波值；增益n用于限制蓄电池电流误差，其大小为为n=Ub/Usc；Ub、Usc分别为蓄电池和超级电容的端电压.

通过保持光储直流微网中母线电压的稳定，可以维持系统的功率平衡.利用LPF 实现HESS 功率分配的控制框图如图2所示.

图2 基于LPF电流分频结构图Fig.2 The structure diagram based on LPF current

2 系统控制策略设计

2.1 有限时间扩张状态观测器

一般的，对于二阶系统有

式中，u为系统输入；y为系统输出；ω为外部扰动；a1、a2为系统参数；b为系统增益；a1、a2、b未知；且有b0≈b.

假设1：对单输入单输出系统的任意可行解，广义扰动f一致有界，且其对时间的导数有界，即

以电压环为例，根据ESO 的设计准则，定义母线电压Udc为状态变量x1，其一阶导数为x2，并将扰动项f扩展为系统新的状态变量x3.则可得系统的状态方程为

定义v1、v2和v3分别为状态变量x1、x2和x3的观测值；e1=v1-x1，e2=v2-x2和e3=v3-x3为相应的观测误差.设计三阶FTESO为：

式中，ξ1＞0；ξ2＞0；ξ3＞0；sig（kφ）=|φ|ksign（φ），k≥0；0.5＜α＜1；ρ=diag（|e1，1|α-1，…，|e1，n|α-1）.

联立式（7）和式（8）得到FTESO的误差方程为

通过选取合适的参数，可以实现对各状态变量的有限时间跟踪.为方便参数整定，根据带宽法［22］将ξ1、ξ2、ξ3分别设计为其中ω0为观测器带宽.

2.2 互补滑模控制器

定义母线电压跟踪误差φe为

式中，Udcref为母线电压参考值.

对式（10）分别求一阶和二阶导数得

广义滑模面Sg设计为

式中，η＞0.

互补滑模面Sc设计为

两个滑模面之间的关系为

式中，S为滑模面之和，即S=Sg+Sc.

依据所选滑模面，互补滑模控制率u设计为

式中，ueq为等效控制器，ure为鲁棒控制器.

等效控制器ueq设计为

鲁棒控制器ure设计为

式中，k1＞0；k2＞0.为了保证快速趋近［23］的同时削弱抖振，在增大k1的同时减小k2.

故完整的CSMC控制率u为

综上所述，光储直流微网混合储能系统总体控制框图如图3 所示.图中，Ipv、Upv、Lpv、Cpv、D和Spv分别为光伏电源侧的电感电流、端电压、电感、滤波电容、二极管和开关管的占空比；Ibat、Ubat、Lbat、Sbat1和Sbat2分别为蓄电池侧电感电流、端电压、电感和开关管的占空比；Isc、Usc、Lsc、Ssc1和Ssc2分别为超级电容侧电感电流、端电压、电感和开关管的占空比；Udc、C和PL分别为母线侧电压、电容和直流负载.

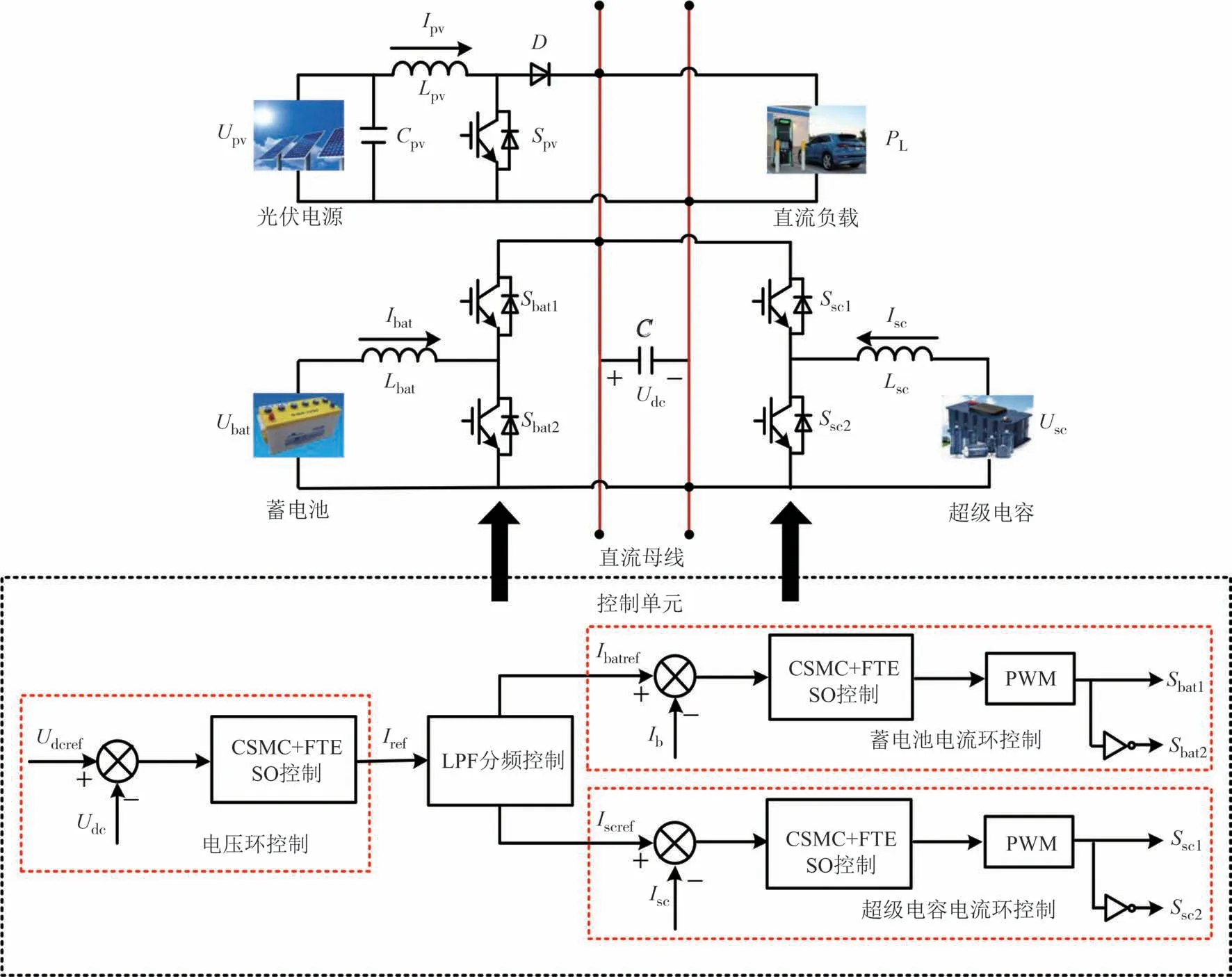
图3 光储直流微网系统控制框图Fig.3 Control block diagram of the optical storage and DC microgrid system

3 稳定性与收敛性分析

引理1：假设非线性系统等式（8）存在一个Lyapunov函数V（x），其中V（x0）表示初值，若满足：

式中，q∈(0.5，1)；a＞0；b＞0；c＞0.

那么系统的轨迹将在有限时间内收敛于以下稳定区域：

式中，μ1∈(0，δ)；μ2∈(0，β).其收敛时间Tr满足［24］：

引理2：给定一个连续可微且正定的函数V（x）：ℝn→ℝ，若对于所有的非零状态x，满足

则系统的状态可以在有限时间内收敛到平衡点，且收敛时间Te满足［25］

式中，V（x1）为Lyapunov函数V（x）的初始值.

3.1 观测器收敛性分析

证明：选择Lyapunov函数V1为

式中，χ=[siga(e1)+e1，e2，e3]T；P为正定对称矩阵.

对χ求导得

矩 阵Ai1的特征 方程为λ3+αξ1λ2+0.5αξ2λ+0.25αξ3ρ-1，其中λ为上述特征方程的特征值.特征方程的Hurwitz矩阵为

根据Routh-Hurwitz 准则，如果选择观测者增益满足ξ1＞0；ξ2＞0；ξ3＞0 且ξ1ξ2-ξ3＞0，则矩阵Ai1为Hurwitz 矩阵.同理，矩阵Ai2为Hurwitz 矩阵。因此，存在对称的正定矩阵P、Qi1和Qi2，满足以下方程：

根据引理1，观测误差在有限时间内收敛到一个小区域，收敛时间T1满足：

式中，σ1∈(0，λ1)；σ2∈(0，λ2).

3.2 控制器稳定性分析

证明：定义Lyapunov函数V2为

对式（33）求导数得

将式（11）、（12）、（18）代入式（34），整理可得

将式（36）代入式（35）得

由引理2可知，总存在两个常数l1、l2，使

式中，l1≤k1+η；l1≤k2.

跟踪误差φe将在有限时间内沿滑模面S收敛到平衡点，有限时间T2满足

综上，电压环在控制率u的作用下能在有限时间T≤T1+T2内收敛到给定参考位置.

4 仿真验证

为验证本文控制策略（FTESO+CSMC）的可行性，基于MATLAB/Simulink 仿真平台，搭建光储直流微网混合储能系统仿真模型，并与其他控制策略进行仿真对比，系统模型参数如表1所示.

系统初始条件设定为：环境温度25 ℃，光照强度1 000 W/m2，低通滤波TLPF为0.005.控制器仿真参数取值如下：

1）FTESO+CSMC 控制，电压环参数：k1=140，k2=10，η=55，α=0.95，ω0=3 140，b0=240；电流环参数：k1=300，k2=10，η=100，α=0.95，ω0=31 400，b0=240.

2）ESO+CSMC 控制，电压环参数：k1=140，k2=10，η=55，ω0=3 140，b0=240；电流环参数：k1=300，k2=10，η=100，ω0=31 400，b0=240.

3）CSMC 控制，电压环参数：k1=140，k2=10，η=55；电流环参数：k1=300，k2=10，η=100.

（4）PI 控制，电压环参数：kp=0.5，ki=15；电流环参数：kp=100，ki=0.5.

4.1 负荷输出功率变化仿真对比

当光照强度维持1 000 W/m2不变，光伏输出以恒功率3 kW运行时，负荷输出功率如图4所示.在电路参数不变的情况下，将不同控制策略进行如下对比分析.

图4 负荷输出功率波动Fig.4 Load output power fluctuation

4.1.1 母线电压仿真对比

图5为负荷扰动时不同控制策略母线电压波形.分析图5 仿真结果可知，在0.7 s 时，负荷功率上升为5 kW，3 kW 的光伏输出不足以满足负荷需求，母线电压下降，此时混合储能单元补偿差额功率，稳定母线电压.在1.0 s 时，负荷功率下降为2 kW，光伏输出功率大于负荷需求，母线电压上升，此时混合储能单元吸收差额功率，稳定母线电压.与其他控制策略相比，FTESO+CSMC 控制在母线电压超调量以及调节时间上均优于其他控制策略.可以有效抑制母线电压波动，提升系统稳定性，验证了FTESO+CSMC控制策略的有效性.

图5 负荷功率扰动时不同控制策略母线电压波形Fig.5 The bus voltage waveform of different control strategies during load power disturbance

4.1.2 蓄电池荷电状态仿真对比

图6 为负荷功率扰动时不同控制策略下蓄电池荷电状态（State of Charge，SOC）容量变化对比图.分析图6 仿真结果可知，当遭到负荷功率扰动，母线电压发生波动时，混合储能系统补偿差额功率.由于蓄电池循环次数有限，为减小蓄电池充放电次数、保护电池寿命，蓄电池的容量变化应越小越好.当蓄电池初始SOC 为80%时，FTESO+CSMC 控制策略下的蓄电池SOC容量变化最小，优于其它控制策略.

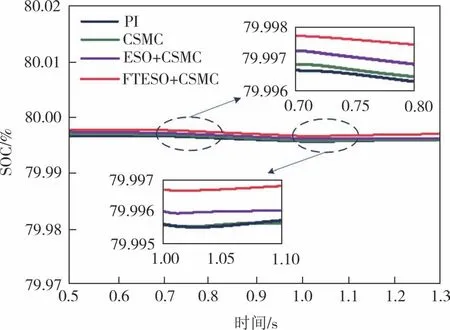
图6 负荷功率扰动时不同控制策略蓄电池SOC容量变化Fig.6 Battery SOC capacity changes in different control strategies during load power disturbance

4.2 负荷功率恒定光照强度变化仿真对比

当负荷以恒定功率2 kW 运行，光照强度发生改变时，光伏电源输出功率如图7 所示.对于光伏功率波动，在电路参数不变的情况下，将不同控制策略进行如下对比分析.

图7 光伏输出功率波动Fig.7 Photovoltaic output power fluctuations

4.2.1 母线电压仿真对比

图8 为光伏扰动时不同控制策略下的母线电压波形.分析图8 仿真结果可知，在0.7 s 时，光照强度从1 000 W/m2降为500 W/m2，输出功率为1.5 kW，小于负荷所需，母线电压下降，此时混合储能单元补偿差额功率，稳定母线电压.在1.0 s 时，光照强度从500 W/m2上升至1 200 W/m2，输出功率为3.6 kW，大于负荷2 kW 的需求，母线电压上升，此时混合储能单元吸收差额功率，稳定母线电压.通过对比母线电压超调量以及调节时间，体现出FTESO+CSMC 控制策略在光伏输出功率扰动下优于其他控制策略，可以有效抑制母线电压波动，提升系统稳定性，验证了FTESO+CSMC控制策略的有效性.

4.2.2 蓄电池荷电状态仿真对比

图9 为光伏功率扰动时不同控制策略下蓄电池SOC 容量变化对比图.分析图9 仿真结果可知，当光伏功率扰动使母线电压发生波动时，混合储能系统补偿差额功率.当蓄电池初始SOC 为80% 时，FTESO+CSMC 控制策略下的蓄电池SOC 容量变化最小，可以更好保护蓄电池寿命，优于其它控制策略.

图9 光伏功率扰动时不同控制策略蓄电池SOC容量变化Fig.9 Battery SOC capacity changes in different control strategies during photovoltaic power disturbance

4.3 电路参数摄动仿真对比

在实际运行工况下，随着运行时长的增加以及系统温度等因素的改变，系统运行元件参数往往会发生变化.为验证FTESO+CSMC 控制策略的有效性，本节对混合储能系统以不同电感电容值运行情况进行仿真对比，以此模拟实际工况下的参数摄动.

4.3.1 电容参数摄动仿真对比

分别使母线电容运行在正常值4 mF 以及3 mF和5 mF，模拟实际运行中的电容参数摄动.电容参数摄动时母线电压仿真波形如图10 所示.仿真条件为：在0.5 s 时，母线电压参考值下降为660 V；1.0 s时，母线电压参考值上升为740 V.通过图10（b）和图10（c）可知，当母线电压参考值发生变化时，FTESO+CSMC 控制策略在不同电容参数下均能稳定追踪期望电压，体现了该策略的动态性和鲁棒性.

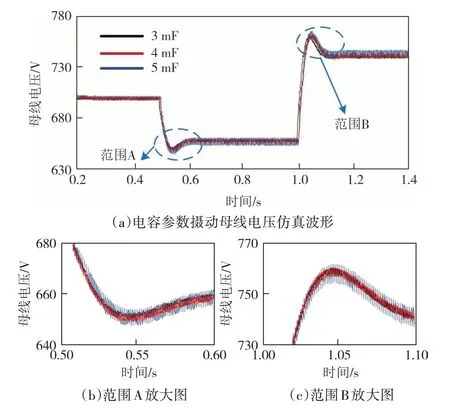
图10 电容参数摄动时母线电压仿真波形Fig.10 The bus voltage during capacitor parameter perturbation

4.3.2 电感参数摄动仿真对比

通过对蓄电池以及超级电容侧分别采用不同数值的电感参数，模拟实际运行中的电感参数摄动，当电感参数为正常值4 mH 以及3 mH 和5 mH 运行时，母线电压仿真波形如图11 所示.仿真条件为：在 0.5 s时，母线电压参考值下降为660 V；1.0 s时，母线电压参考值上升为740 V.通过对比图11（b）和图 11（c）仿真结果可知，当母线电压参考值发生变化时，不同电感参数下该系统均能稳定追踪期望电压，体现了FTESO+CSMC控制策略具有较好的鲁棒性.

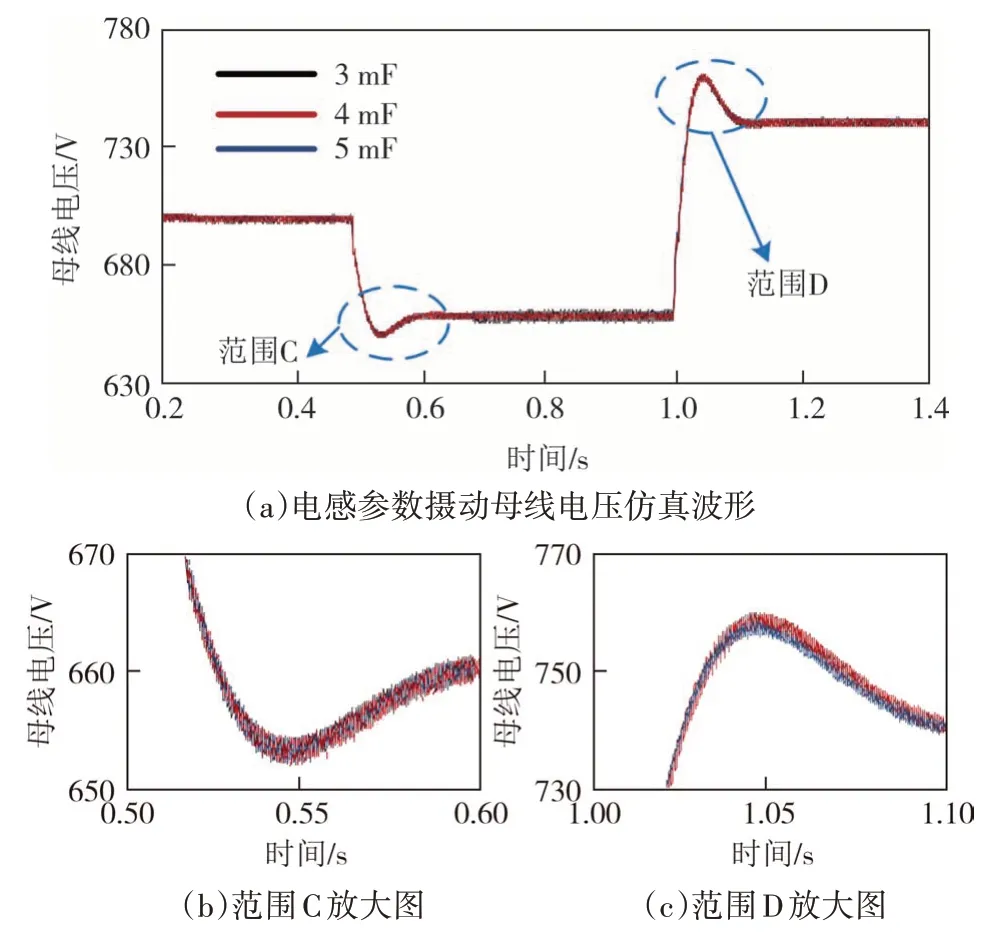
图11 电感参数摄动时母线电压仿真波形Fig.11 The bus voltage simulation waveform during inductance parameter perturbation

5 结论

本文以光储系统母线电压为研究对象，结合有限时间扩张状态观测器和互补滑模，设计控制器，并与其他控制策略进行仿真对比，得到以下结论：

1）有限时间观测器确保了母线电压能在有限时间内实现参考信号的跟踪，提高了扰动估计速度.

2）将扰动观测值作为前馈输入互补滑模误差反馈控制中，既提高了系统的动态响应性能，又提高了系统的抗扰能力.

3）仿真结果表明，本文所提策略在多种工况下的表现均优于其他策略，体现了FTESO+CSMC 的优越性.