基于多目标协调的混合储能功率自适应分配方法

陈燕东 ，刘燕军 ，张松 ，谢志为 ，2，王自力 ，2，桑勇 ，张龙

（1.湖南大学 电气与信息工程学院，湖南 长沙 410082；2.湖南大学深圳研究院，广东 深圳 518000）

以风电和光伏为主的分布式微网在海岛电源、铁路供电、野外供电等场景应用广泛［1-3］.分布式电源受限于可再生资源的时空零散分布，出力具有间歇性.同时，负荷的随机投切也会导致微网母线功率供需失衡［4］.将混合储能接入微网，可以调控母线的功率潮流，增强孤岛电力的运行稳定性［5-7］，但储能的功率控制及子单元的功率分配问题带来了新的挑战.通过电能的吸收释放，储能向孤岛电力提供功率补偿［8］，例如在发电功率突减时放电、突增时充电，实现母线功率的“降余补缺”［4］.谢志佳等［9］认为电池储能具有的动态吸收并释放能量的特性能补偿母线功率缺额，是孤岛电力的必要功率补充.Liu 等［10］、叶小辉等［11］、陶琼等［12］详细叙述了分布式电力中储能的作用，分析了各类储能的优缺点及应用性，肯定了储能的响应速度快、稳定性高、可控性强等优点，同时指出储能的最大出力受其SOC（荷电状态）影响.

混合储能对外的整体功率响应能增强微网对母线功率潮流的调控，但对内的子单元功率响应决定混合储能的整体输出性能.针对子单元功率分配，文献［13-17］控制超级电容补偿失衡功率的高频分量与蓄电池响应低频分量，减少了母线的功率扰动，但未考虑子单元间的功率协调，并没有解决蓄电池频繁充放电与功率抵消问题.文献［18-19］通过SOC均衡控制有效平衡了各子单元出力.文献［20］基于深度学习不断优化容量与功率的关联函数，实现了功率的精确解算，但其浩大的计算量不适合微嵌入式工程.文献［21-23］通过约束超级电容电压来调节蓄电池的出力，极大简化了功率分配的计算流程.由上分析可知，在设计功率分配算法时，很容易忽略子单元的功率与能量特性对整体功率响应的影响，同时应简化控制流程，提高程序的容错率，无论是分频还是深度学习，其执行的容错率都较低.因此充分利用储能单元的固有特性，提高子单元间的功率协调控制仍值得深入研究.

对此，本文提出一种基于多目标协调的混合储能功率自适应分配方法，从功率和能量特性视角调控混合储能的功率响应.实现的功率分配效果符合子单元的功率响应特性；通过SOC 管理优化子单元的功率曲线，保障了超级电容作为主电源的功率输出能力，降低了蓄电池的充放电深度，提高了混合储能的整体功率响应能力.

1 微网结构

图1 给出了微电网的结构框架.分布式发电源和消耗源并联接入母线；超级电容和蓄电池经由变流器接入母线，组成混合储能；F2 为并网开关，非必要工况下不闭合（例如，仅在储能单元无法工作时闭合），这使微网处于类孤岛状态.图中箭头表示各单元的功率流动正方向.

忽略各级变流器损耗，如图1 所示微网稳定运行时各功率源间的功率平衡方程见式（1）.

式中，Pbat是蓄电池输出功率，Psc为超级电容功率；Pse为光伏并网功率，Pwe为风电并网功率；∑Pload表示总负荷能耗功率.

将储能作为主功率源，可将母线功率潮流分为储能与非储能性质功率流，式（1）可变换为式（2）.

式中：Pnet为母线净需求功率，表示储能补偿功率.由式（2）可知：混合储能的功率响应等于负荷能耗与分布式发电源并网功率之差时，母线功率平衡.

2 混合储能功率控制系统设计

2.1 混合储能的功率控制方案设计

孤岛工况下，微网缺少大电网支撑，可将储能设为电压源，用于电压调节和功率支撑［24］.

超级电容是功率型单元，能响应瞬时大功率需求，但其能量密度小，这限制了其持续输出性能.蓄电池是能量型单元，常在站点配置大容量组合，但其功率响应速度慢.针对储能的固有功率与能量特性，设计的功率控制方案如图2所示.

图2 混合储能系统功率控制模型Fig.2 Power control model of hybrid energy storage system

通过对不同储能特性的“优势整合，劣势互补”，上述功率控制方案的思路是发挥超级电容的瞬时大功率响应特性，维持母线功率动态平衡，通过功率管理单元将超级电容的功率响应转移至蓄电池输出，实现补偿母线功率的同时完成子单元间的功率分配.

2.2 混合储能主从并联功率控制

基于图2 描述的功率控制思路，设计了主从并联型混合储能功率控制方案，超级电容作为主控电压源，采用V/f策略；蓄电池作为从控制器，采用直接功率控制.通过控制整体储能系统的功率响应，能满足母线的电压调节和功率补偿需求.

图3 给出了采用PI 控制的简化控制系统电路，变流器的控制参数见表1.超级电容采用端电压为Udc1的电容和电阻Rsc的串联模型等效；Udc2为蓄电池电压；Qn、Kn（n=1～6）为开关管及开关信号；ea～c为变流器桥臂中点电压；iLai～Lci、ioai～oci（i=1，2）分别表示a、b、c 三相滤波电感电流和并网电流；ua～c为母线相电压；Lfi、Rfi和Cfi（i=1，2）表示LC 滤波器的结构参数.母线电压等级为380 V/50 Hz.

表1 变流器控制参数Tab.1 Parameters of converter control systems

图3 混合储能控制系统简化电路Fig.3 Simplified control circuit for hybrid energy storage system

蓄电池侧的P/Q 控制形式为双层功率外环和电感电流内环，表现为电流源特性.kppob和kipob、kppb和kipb、kpib和kiib分别表示外层功率环、内层功率环和电流环的PI 控制器的比例、积分参数；id2和iq2、iod2和ioq2、ud2和uq2表示电感电流、并网电流和母线电压的dq分量；ω0、θ为对母线电压锁相所得的频率与相角；外层功率环以并网电流（iod2、ioq2）为计算因子，内层功率环以电感电流（id2、iq2）为计算因子，外层功率环控制并网功率，内层功率环输出作为电流环指令，可使电流指令变化更平滑.

由基尔霍夫电流定律（KCL）易推导出交流侧电路的功率表达.

式中，ioa2～oc2、iLa2～Lc2、iCa2～Cc2分别表示交流侧并网电流、电感侧电流和电容侧电流信号；Pbat和Qbat、PbL和QbL、PbC和QbC分别表示计算的并网功率、电感侧功率和电容侧功率.分析式（3）～式（4）可知，双层功率策略满足交流侧电路KCL 方程，补偿了LC 滤波器的功率损耗，能提高并网功率的控制精度.

超级电容侧的V/f控制形式为电压外环和电感电流内环，表现为电压源特性.kpis和kiis、kpus和kius分别表示电压外环和电流内环的PI 控制器的比例、积分参数；id1和iq1、iod1和ioq1、ud1和uq1分别表示电感电流、并网电流和母线电压的dq分量；ud1*和uq1*、ω和f*表示用于构造电压特性的电压幅值与频率参考.

式（5）计算超级电容的并网功率Psc、Qsc.

3 基于多目标协调的功率自适应分配

图4 给出了基于多目标协调的混合储能功率自适应分配方法，实现了四个维度的功率协调：

图4 基于多目标协调的子单元功率自适应分配模型Fig.4 Adaptive power allocation method with multi-objective coordination for hybrid energy storage

1）基于SOC状态的最大功率响应协调，对应Pbm（s）模块.

2）判断功率指令充放电状态的超级电容功率协调，对应Pscb（s）模块.

3）考虑超级电容SOC 优化的蓄电池功率协调，对应Pbf（s）、Pbs（s）模块.

4）混合储能子单元的功率自主分配设计，对应Pi（s）、H（s）模块.

3.1 储能最大输出功率协调设计

3.1.1 储能SOC状态的分层设计

相较于大电网，储能的可用容量很小，长时以最大功率充放电易发生SOC 越限，造成不可逆的使用损害.因此有必要对SOC 特性分层管理，约束不同SOC 状态下的充放电能力，这可以有效保护储能单元，延长使用寿命.

图5定义了储能的SOC区间及其分界值：

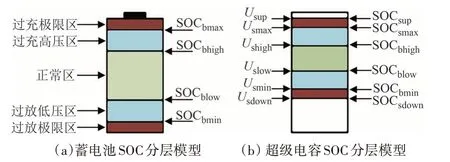
图5 储能SOC特性区间示意图Fig.5 Schematic diagram of SOC characteristic interval

在典型的三分区管理（过充警戒区、正常区和过放警戒区）基础上［24］，本文将警戒区细分为高/低压区和极限区，既能有效防止SOC 越限，又能备用部分极限容量，提高SOC利用率.

超级电容作为主电压源，要求其在SOC 处于警戒区甚至极限区时仍满足母线电压的调控需要求，因此将其SOC分为7大区间，增加了顶层区（＞SOCsup）和底层区（＜SOCsdown）为限制区间.

3.1.2 基于蓄电池SOC的最大功率协调系数设计

超级电容是物理型储能，SOCscn状态约束其功率响应强度，对使用寿命的影响较小；蓄电池是电化学储能，SOCbn越限会造成内部介质的化学活性降低，严重缩短其使用寿命［18，25］.因此，需限制不同SOCbn下蓄电池的最大充放电功率，式（6）通过设置协调系数λ约束蓄电池的最大功率响应：

式中，Pbm、Pbatm分别表示蓄电池的额定最大功率与协调后的可用最大功率；λ为最大功率协调系数，表征最大功率响应的约束状态.

蓄电池的端电压与其SOCbn表现为非线性关联［25］，据此选用幂函数特性表征其最大功率与SOCbn的关联，λ的数学表达如下：

式中，SOCbmid=（SOCbhigh+SOCblow）/2；SOCbn为蓄电池当前SOC 状态；λ1、λ2表示放电与充电功率协调系数.由式（7）可绘制λ曲线，见图6，其左纵坐标轴对应λ1，右坐标轴对应λ2.

图6 基于SOCbn的功率系数λ曲线Fig.6 λ curve based on SOCbn state

图6 表征蓄电池在不同SOCbn下对应的λ曲线，SOCbn与λ1、λ2表现为 一一对应.观察λ1可知：当SOCbn减小至SOCbmid时，λ1从1开始下降，λ1的变化表现为幂函数趋势（与蓄电池电压特性一致），当SOCbn减小至SOCbmin时，λ1降为0，此时蓄电池的可用放电功率为0.λ2特性同理分析.

3.2 判断指令充放电状态的超级电容功率协调设计

3.2.1 超级电容SOC的二次计算

超级电容的SOC 状态与其端电压近似为正相关特性，常采用开路电压法估算SOCscn［25］.

式中：Uscn为超级电容端电压，Usc_max、Usc_min为超级电容额定的最大与最小电压.

作为主控电压源，要求超级电容在极限SOCscn状态下具有正常的充放电功率响应能力，而式（8）通过剩余容量与额定容量的比值定义SOCscn，显然在较低SOCscn时超级电容的放电能力弱，较高SOCscn下的充电能力不合要求，与设计要求相悖.

本小节优化了SOCscn的计算过程，式（9）重构了式（8）中的关键变量：二次配置Usc_max、Usc_min参考值，使超级电容满足设计要求.

SOCscn二次计算是按需将Usc_max、Usc_min缩小和放大为Usup和Usdown，见图7，通过重构相关的电压参考，使之具备极限SOC下的充放电能力.

图7 超级电容的最值电压二次配置Fig.7 Reconfiguration of voltage reference for SC

3.2.2 超级电容功率协调模式

蓄电池频繁切换充放电状态将严重缩短其使用寿命，但超级电容几乎无此限制［25］，因此通过判断蓄电池功率指令的充放电状态，在满足SOCscn约束下允许超级电容协调蓄电池的部分功率响应，能有效降低蓄电池的功率响应深度.

图8 描述了超级电容协调模式的SOCscn约束：SOCcoo表示功率协调模式下超级电容的SOC约束值，SOCscn≥SOCcoo时超级电容允许放电协调，SOCscn≤SOCcoo时允许充电协调.

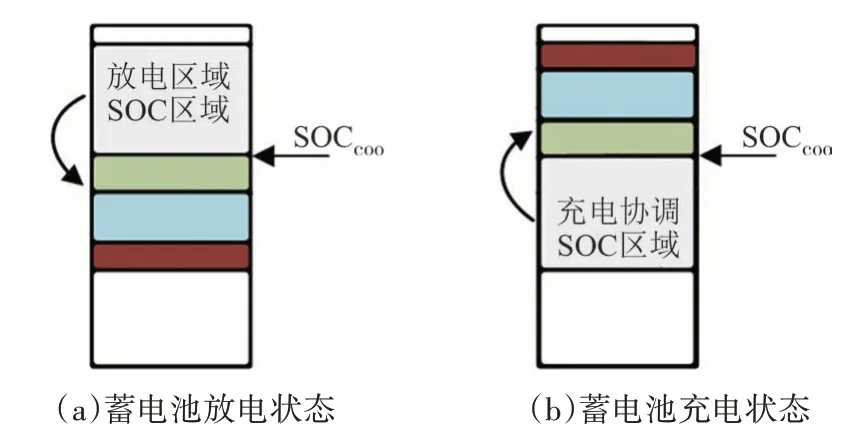
图8 超级电容功率协调示意图Fig.8 The diagram of power coordination of SC

用式（10）表示图8，其中Pscb2、Pscb1为充电与放电协调功率，Pgbbi（i=1，2）为协调功率计算值.

超级电容SOCscn与其端电压近似为正相关特性［25］，可采用正比例特性描述协调功率Pgbbi（i=1，2）随SOCscn的变化，设Pb为蓄电池的一次功率指令.

式中：Pgbb1表示放电协调时，超级电容的放电功率指令；Pgbb2表示充电协调下的充电功率指令.

根据式（11）绘制Pgbb曲线，见图9.

图9 Pgbb随SOCscn变化特性曲线Fig.9 Characteristic curve of Pgbb changing with SOCscn

超级电容的功率协调控制发挥不同SOCscn下的超级电容的充放电的输出优势，以释放蓄电池的部分功率响应，同时调节自身SOCscn状态.

3.3 考虑超级电容SOC 优化的蓄电池功率协调设计

储能充放电能力随其SOC 变化为反特性［25］，如过充时其放电能力增强而充电能力减弱；过放时其充电能力增强而放电能力减弱.超级电容作为电压源，其功率响应决定混合储能的瞬时功率输出，直接影响微网的运行，因此需要优化SOCscn状态，保障其正常的充放电能力.

设SOCscn处于正常区时，蓄电池进入常态模式，常态功率指令为Pbatr，当SOCscn偏离正常区时，蓄电池进入协调模式，协调功率指令为Pbs.令全状态SOCscn下的蓄电池功率指令为Pbf.

式中，P1=Pnet-Pscmax；P2=Pnet-Pscmin.Pscmax、Pscmin是超级电容的最大放电与充电功率.结合式（13），绘制了Pbs特性曲线，如图10所示.

图10 Pbs随SOCscn变化特性曲线Fig.10 Characteristic curve of Pbs changing with SOCscn

当SOCscn偏移正常区，蓄电池进入功率协调模式，Pbs的强度取决于SOCscn的偏移深度；当SOCscn进入极限区，蓄电池以功率P1（或P2）作为协调功率指令，此时超级电容的响应功率为Pscmax（或Pscmin），SOCscn能以最快速度回到正常区.

3.4 混合储能子单元功率自主分配方法

图2 描述的功率控制方案中，功率管理单元实现储能子单元功率分配.以积分器为控制单元，设计了如图11所示的功率自主分配方法.

图11 中，Psc为超级电容的并网功率；Pbatr为蓄电池的一次功率指令；PH为超级电容余功率指令；Pb为过程指令.现分析各函数具体内容.

式中：功率分配函数Pi（s）的本质为积分器.

式中：对应Pbm（s）函数，Pbmax、Pbmin为蓄电池可用最大放电与充电功率，对应式（6）中Pbatm.

式中：该式对应函数H（s），表示余功率函数，当蓄电池满功率输出也无法补偿母线净需求功率Pnet时，超级电容承担余下的功率缺额PH.

建立图11对应的传递函数.

假设母线功率平衡且Pb未超调，可得H（s）=0，此时图11处于开环状态，式（17）可简化为式（18）.

积分器对输入信号具有时间累加和空间调零作用，简称“时空调零”特性，频域上表现为高频滤除和时域上表现为延时，即：经式（18）若干周期调节后，稳态下Pbatr（s）以Psc（s）输入的满幅输出，且Psc（s）=0，调节周期由Ki控制.

结合式（2）可导出功率自主分配下的储能子单元的功率指令表达：

t1时刻母线净需求功率Pnet发生单位阶跃增变化，子单元的功率响应如图12所示.

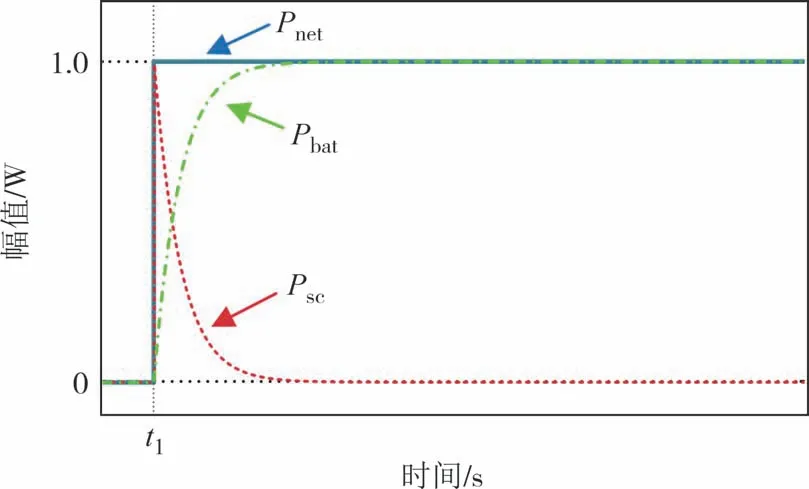
图12 Psc和Pbat的功率响应曲线Fig.12 Power response of Psc and Pbat

t1时刻Pnet阶跃突变，超级电容迅速响应，提供峰值功率补偿，再渐减为0，蓄电池功率Pbat则从0 渐增为1，承接了超级电容的功率转移.

综上可知，当母线功率失衡，超级电容补偿瞬时Pnet缺额，等效为Pnet的高频分量，经过Pi（s）调节后高频响应Psc以低频化信号Pbatr转移至蓄电池输出，等效为Pnet的低频分量.表明在该功率控制方案下，子单元的功率响应能自主分配.

4 仿真验证

基于Matlab/Simulink 平台，搭建基于多目标协调的混合储能功率自适应分配方法仿真模型.

参数定义：设系统总需求功率为200 kVA，允许发生20%波动，可设母线功率波动为±40 kW；选取A123-ANR26650M1 型锂电池，单体参数为3.3 V/ 2.3 Ah，通过360 节串联成列作为一组蓄电池；选取HCCap-48 V/200 F 模组串并联，得到额定电压为 1 248 V 的超级电容单体，据此设置混合储能的仿真模型（小容量仿真有助于监测SOC动态变化）.

储能单元的参数如表2 所示.仿真对比如图13所示.设置三种功率分配策略仿真对比，1 号策略仿真子单元功率自主分配模式，见图13（a）；2号策略仿真子单元功率自主分配+超级电容功率协调模式，见图13（b）；3 号策略仿真基于多目标协调的功率自适应分配模式，见图13（c）.

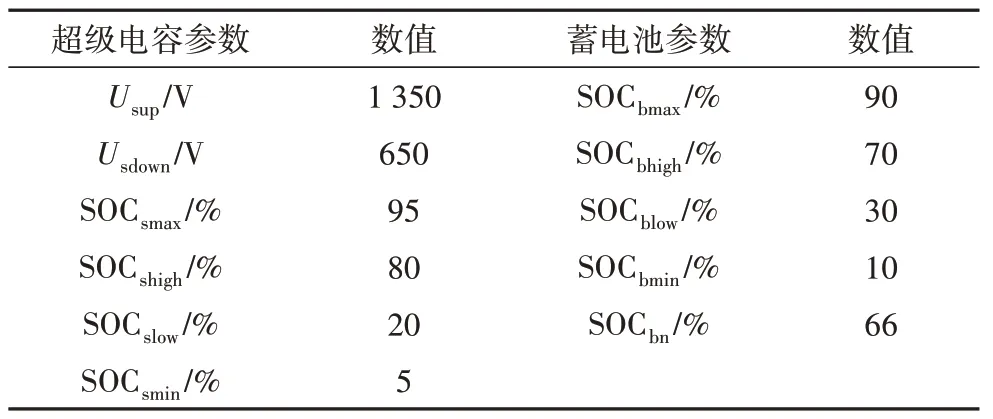
表2 储能单元设置参数Tab.2 Parameters of the energy storage

图13 仿真设置的三种功率分配策略Fig.13 Three power allocation strategies for simulation

将t0时刻定义为3 号策略中超级电容的首动作时刻，仿真波形图中的小号蓝色圆圈及文字表示此刻功率分配模式发生切换.

工况1：当分布式发电单元新能源受实况条件影响而造成出力骤减，母线净需求功率Pnet表现为突增变化.设t1时刻Pnet由平衡状态阶跃增为35 kW.设置超级电容SOCscn在全状态下进行仿真，波形输出见图14～图18.

图14 初始SOCscn=97%时输出波形Fig.14 System waveform when initial SOCscn=97%

图14 中初始SOCscn=97%，t1时刻净需求功率Pnet由0 突增为35 kW.在稳态下，图14（a）表明三种策略均能稳定补偿Pnet缺额，由蓄电池承担全部功率缺额，超级电容不发生功率交互；从图14（b）中可知，2 号与3 号策略中SOCscn最终维持在设定的安全区，而1号策略中超级电容始终处于过充状态.

在暂态调节中，1号策略输出的功率曲线符合自主分配设计原则：在t1时刻，超级电容输出35 kW 功率补偿母线功率的瞬时缺额，在自主分配控制下Pnet平滑转移至蓄电池，稳态后超级电容进入待机状态，对应图14（b）中SOCscn维持在过充极限区.2 号策略进入超级电容功率协调模式（协调蓄电池放电）：在t1～t3时刻，SOCscn≥SOCshigh，超级电容承担全额Pnet需求，SOCscn下降，蓄电池处于待机状态；t3时刻后，SOCscn＜SOCshigh，蓄电池开始承担Pnet需求，此时Psc随SOCscn降低而减小，Pbat随SOCscn降低而增加，SOCscn的负变化率逐渐减小，至Psc=0、Pbat=Pnet，此时SOCscn=SOCsmid，超级电容退出功率协调模式，系统进入稳态.3 号策略中：超级电容处于过充极限状态，在t0～t2时刻，SOCscn≥SOCshigh，蓄电池进入充电协调模式，该模式下蓄电池的充电功率由SOCscn约束，不受Pnet强度影响，此时超级电容以大功率放电，使SOCscn快速下降，t1时刻Pnet阶跃突增后超级电容迅速动作，在Psc曲线上表现为功率尖峰；t2时SOCscn=SOCshigh，蓄电池退出功率协调模式；t2时刻后3 号策略进入超级电容功率协调模式，该过程与2 号策略一致.图14 表明：在功率自主分配策略基础上，多目标协调策略与仅考虑超级电容协调策略都能调节超级电容SOCscn状态，但前者对SOCscn优化的能力更强.如在t3时刻，后者仅将SOCscn优化至80%，而前者将SOCscn优化至71.92%，其SOCscn优化性能相较后者提高了10.10%.

图15 中初始SOCscn=83%，在t0～t2时刻，3 号策略中蓄电池进行充电协调，t2时刻后超级电容进入放电协调.2 号策略中超级电容一直处于放电协调模式。t3时刻，2 号与3 号策略中SOCscn=SOCshigh，t3时刻后两种策略的运行过程一致.由于（t1-t0）很小，因此相比于2号策略，3号策略对SOCscn的差额优化有限，仅为1.24%.

图15 初始SOCscn=83%时输出波形Fig.15 System waveform when initial SOCscn=83%

图14～图15 表明：SOCscn偏移越深，多目标协调策略的SOCscn优化能力越强，如图14～图15 中的SOCscn偏移深度加大，在仅考虑超级电容协调策略将SOCscn优化至SOCshigh时，所提多目标协调策略对SOCscn的差额优化效果从1.24%提高至10.10%.

图16中初始SOCscn=53%，2号与3号策略进入超级电容功率协调模式，运行过程一致.1 号策略的暂态调节最快，但超级电容SOCscn状态最差.

图16 初始SOCscn=53%时输出波形Fig.16 System waveform when initial SOCscn=53%

图17 中初始SOCscn=23%，处于正常区，系统进入功率自主分配模式，3种策略输出一致.

图17 初始SOCscn=23%时输出波形Fig.17 System waveform when initial SOCscn=23%

图18 中初始SOCscn=3%，处于过放极限状态.在放电模式下，2 号与1 号策略进入功率自主分配模式，但无法调节SOCscn状态；3 号策略进入蓄电池放电协调模式（协调优化SOCscn状态），将SOCscn调节到正常区（SOCscn≥20%）.图18 表明：设计的SOC 管理和多目标功率协调使超级电容具备了极限SOC 状态下的功率输出与SOCscn优化能力.

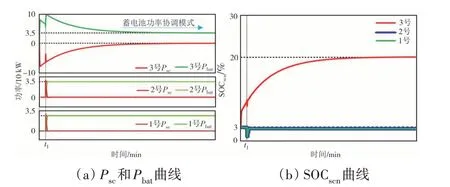
图18 初始SOCscn=3%时输出波形Fig.18 System waveform when initial SOCscn=3%

上述结果验证了基于多目标协调的混合储能功率自适应分配方法的可行性，仿真输出的功率响应曲线中所表现出的功率特性符合超级电容和蓄电池的功率响应特性；在功率自主分配策略的基础上，多目标协调策略加强了对不同SOCscn状态下的超级电容的功率响应性能的利用，降低了蓄电池的总电能输出强度；所设计的SOC 特性分层管理，加强了对超级电容SOCscn状态的优化调节，使超级电容在全SOCscn状态下具备充放电能力.这有效增强了混合储能的整体功率响应能力.

工况2：模拟母线净需求功率Pnet脉动式突变场景，见图19（b），t1时刻Pnet从+10 kW 突变为-30 kW后快速恢复为+10 kW，t2时刻Pnet从+10 kW 突变为+50 kW 后快速恢复为+10 kW.设置超级电容SOCscn处于正常状态.仿真1号和3号策略如图19（a）所示.

图19 工况2下系统输出波形Fig.19 System output waveform of simulation 2

图19 中，Pnet发生正负极性变化的高频脉动突变.t1时刻Pnet突变过程发生了两次极性切换，3 号策略中Pbat未发生充放电状态转换，而1 号策略发生了两次状态切换.t2时刻Pnet突增中伴随高频变化的小扰动功率信号，相比1 号策略，3 号策略的Pbat曲线中，功率调整时间从t3增至t4，蓄电池的最大功率深度从39.4 kW 降至21 kW，降低了46.70%.图19 表明，多目标协调策略有效减缓了蓄电池的功率变化，降低了蓄电池的功率响应深度.

在功率协调模式下，混合储能在响应高频过零变化的功率时，有效减少子单元正负性功率抵消造成的功率浪费情况，这降低了子单元的功率响应深度，增强了混合储能的功率补偿性能.对蓄电池而言，实质上是加强其使用性能，延长其使用寿命.

5 结论

本文对应用于孤岛微网中的混合储能的整体功率响应控制及子单元功率分配问题开展研究，提出一种基于多目标协调的混合储能功率自适应分配方法，实现了子单元功率在4 个维度协调的自适应分配控制，总结如下：

1）设计了一套可应用于孤岛电力系统中的混合储能整体功率控制方案，能调节母线的功率潮流和自适应分配子单元功率.

2）所提自主分配策略下的功率输出符合子单元的功率响应特性，超级电容响应瞬时功率需求，蓄电池承担超级电容的转移功率，其功率曲线缓慢变化，等效于承担稳态的功率需求.

3）在自主分配策略基础上，提出了多目标协调策略来加强子单元SOC 管理与功率协调.实现了当SOCscn处于极限区时，利用蓄电池优化SOCscn，相比于仅考虑超级电容功率协调，多目标协调下的SOCscn优化性能最大能提高10.10%；当SOCscn处于正常区时，利用超级电容协调蓄电池的功率输出，减小了蓄电池的充放电状态转换次数与功率深度，以工况2 为例，多目标协调下蓄电池的充放电转换次数减少2次和功率响应深度降低了46.70%.