基于新型相似日选取和VMD-NGO-BiGRU 的短期光伏功率预测
王瑞,张璐婷,逯静
(河南理工大学 计算机科学与技术学院,河南 焦作 454000)
太阳能是可再生能源中最丰富、发展潜力最大的清洁能源,其开发与利用已经成为我国能源结构调整的重要方向[1].光伏发电具有间歇性、随机性和波动性,由此给电网的安全运行带来了一系列问题,受到了各界的广泛关注[2-3].随着新型电力系统建立,电网建设滞后于光伏电力的生产,“弃光”、“限电”问题加重,可能降低原始数据在预测模型中的可信度,从而进一步增加短期的预测难度[4].在“碳达峰”“碳中和”的战略背景下,我国电力结构清洁化趋势将更加凸显[5],光伏并网对电网的影响也越来越显著.开展光伏发电功率超短期预测,能有效降低光伏出力不确定性给电网带来的影响,提高光伏发电系统的可靠性[6].
预测光伏功率的方法多种多样,叶林等[7]基于气象因素与光伏功率波动特征的关联性,将天气过程划分为5 种类型,并基于变分模态分解算法,将光伏功率分解为类晴空过程和波动过程,构建的预测模型提高了光伏功率预测准确性,验证了对天气进行划分的有效性.张金金等[8]通过模糊C均值聚类算法对数据进行聚类,获得较好的数据分类结果,但未考虑气象因素的影响.王福忠等[9]提出在第一阶段采用变分模态分解(VMD)分解原始功率并建立LSTM 模型进行预测,第二阶段对误差序列进行误差补偿预测,与上一阶段预测结果叠加,得到最终预测结果.孟安波等[10]考虑到不同天气因素影响,通过加权模糊聚类对天气类型进行划分,筛选相似日数据集,采用纵横交叉算法优化改进的高斯过程回归模型的超参数,对光伏功率进行预测.杨国华等[11]采用模糊C 均值聚类算法选取相似日,结合灰狼优化算法优化小波包神经网络和AdaBoost 算法,建立预测模型.
基于上述分析,虽然预测精度和效率与早期的预测模型相比有了很大的突破,但在处理不同气候条件时,光伏功率预测模型的预测性能和鲁棒性仍然存在不足.为了从大量数据中选取与预测日相似的历史日,以及考虑到相关性越强的影响因素对于光伏功率预测结果影响越大,本文提出一种基于相似日选取,结合利用北方苍鹰优化算法优化BiGRU参数的混合预测模型.首先,通过斯皮尔曼相关系数法筛选出影响最大的气象因子,通过VMD 分解将原始光伏功率和影响最大的气象因子分解重构为一系列子信号;其次,将气象因子分解后的分量重构,并对影响因素重新定义,根据构建新的评价指标筛选出相似日数据集;然后利用一组BiGRU,建立以相似日子信号为网络输入的深度学习模型,并利用NGO对每个BiGRU 网络的超参数进行有效优化.最后通过算例仿真,证明了该模型的有效性.
1 算法原理
1.1 光伏发电功率影响因素
光伏功率主要受到辐照度、环境温度、湿度、气压等多种气象因素影响[12],不同的气象因素对光伏发电功率的影响程度也不同.对影响光伏发电的变量进行相关性分析,筛选出主要特征.
通常采用的皮尔逊相关系数需要满足正态分布,但是对于波动性比较强的光伏发电功率,大多数影响因素并不符合正态分布.图1 是光伏功率的概率密度分布图,图中概率密度曲线为非正态分布,因此斯皮尔曼相关系数是相对较好的选择.斯皮尔曼相关系数的定义如下:
式中:di表示第i个数据对应的位次值之差,n表示总的观测样本数.
斯皮尔曼相关系数可以衡量两个变量之间的相关性,它将数据按序给出等级,若有数据数值相同时,则将计算数值等级的平均值作为等级数.同理,计算另一组数据的等级排序,得到等级大小,之后计算两组数据等级差,代入式(1),即可得出相关系数,可以方便应用于非正态性的数据.
本文选取2022 年江苏某光伏电站实际数据进行相关性分析,影响因素有总辐射、散射辐射、环境温度、气压以及湿度.根据斯皮尔曼相关系数计算出各因素与光伏功率的相关系数.具体数据如表1所示.

表1 各因素与功率的斯皮尔曼相关系数Tab.1 Spearman correlation coefficient between various factors and power
1.2 变分模态分解
VMD 为避免信号分解过程中出现模态混叠,在计算本征模态分量时舍弃了传统信号分解算法所使用的递归求解的思想,采用完全非递归的模态分解.与传统信号分解算法相比,VMD 拥有非递归求解和自主选择模态个数的优点,其核心思想是构建和求解变分问题[13].
1)构建变分约束模型:
式中:f(t)为原始功率信号;uk为各分量;ωk为各分量对应中心频率;δ(t)为脉冲信号.
2)通过引入拉格朗日算子λ和二次惩罚因子α,求解约束变分问题:
对各分量uk及ωk通过交替方向乘子法交替更新,完成分解.
式中:n为迭代次数分别代表f(t)、u(t)、λ(t)的傅里叶变换.
1.3 双向门控循环单元
BiGRU 模型采用了循环神经网络(RNN)的结构,其中每个RNN 单元都是由一对门控循环单元(Gated Recurrent Unit,GRU)组成.与长短期记忆网络(Long Short-Term Memory,LSTM)相比,GRU 不仅减少了网络参数,而且保持了LSTM 的良好性能[14].GRU的结构如图2所示,计算公式如下:

图2 GRU网络结构图Fig.2 GRU network structure diagram
式中,rt、zt表示重置门和更新门;σ为Sigmoid 激活函数;W和U表示权 重矩阵;表示中 间记忆状态;φ(·)表示非线性激活函数;⊗表示哈达马积;ht-1表示上一时刻的隐藏状态信息;xt表示输入序列中的第t个元素.
BiGRU 由两个方向相反的GRU 组成[15],在本模型中采用单层BiGRU.在BiGRU 模型中,输入序列首先被分别输入到两个方向的RNN 中.每个神经网络都包含一个隐藏层,用于存储序列中的信息.在前向RNN中,输入序列从左到右进行处理,每个时间步的输出结果都会被传递到下一个时间步.在后向RNN中,输入序列从右到左进行处理,每个时间步的输出结果也会被传递到下一个时间步.这样,每个元素在正向和反向的GRU 中都被处理了一次,以提取更全面的特征信息.BiGRU结构如图3所示.

图3 BiGRU网络模型Fig.3 BiGRU network model
BiGRU的计算公式如下:
式中:GRU(·)表示门控循环单元;xt为输入;分别为前向和后向隐藏层输出状态;αt和βt分别表示前向和后向隐藏层的输出权重;表示前向隐藏状态在前一个时刻的隐藏状态;表示后向隐藏状态在后一个时刻的隐藏状态;bt为偏置值.
1.4 北方苍鹰算法
北方苍鹰优化算法于2022 年提出,该算法模拟了北方苍鹰在捕猎过程中的行为,具体包括猎物识别与攻击、追逐及逃生等行为.北方苍鹰优化算法可包含两个阶段[16]:第一阶段,在识别出猎物后,它以高速向猎物移动攻击;在第二阶段,追逐猎取猎物.
1.4.1 初始化
初始化种群.以下矩阵代表的是北方苍鹰的种群数量矩阵:
式中:X为北方苍鹰的种群矩阵;Xi为第i个北方苍鹰的位置;xi,j为第i个北方苍鹰的第j维的位置;N为北方苍鹰的种群数量;m为求解问题的维度.
在北方苍鹰优化算法中,求解问题的目标函数可以用来计算北方苍鹰的目标函数值,表示如下:
式中:F为北方苍鹰种群的目标函数向量;Fi为第i个北方苍鹰的目标函数值.
1.4.2 识别猎物及攻击猎物
北方苍鹰在捕猎的第一阶段是随机选择一个猎物,并进行攻击.由于在搜索空间中对猎物的选择是随机的,因此这一阶段增强了NGO算法的勘探能力.该阶段对搜索空间进行全局搜索,以确定最优区域.在这一阶段,北方苍鹰进行猎物选择和攻击的行为,用式(12)~(14)描述:
式中:Pi为第i个北方苍鹰的猎物的位置;FPi为第i个北方苍鹰的猎物的位置的目标函数值;k是[1,N]范围内的随机整数为第i个北方苍鹰的新位置;为第i个北方苍鹰的第j维的新位置为基于第一阶段更新后第i个北方苍鹰的目标函数值;r是[0,1]范围内的随机数;I为1或2的随机整数.
1.4.3 追逐及逃生
猎物受到北方苍鹰攻击会试图逃跑.因此,在追逐猎物的收尾过程中,北方苍鹰需要继续追逐猎物.北方苍鹰高速追击并抓捕猎物行为的模拟,提高了算法的局部搜索能力.假设这种狩猎活动接近于一个半径为R的攻击位置.在第二阶段中,用式(15)~式(17)描述:
2 基于灰色关联度的相似日选取
2.1 灰色关联度
由于不同气象因素对光伏功率的影响程度不同,在构建新的综合评价指标时,应该对影响程度更大的气象因素赋予更大的权重.而灰色关联度就是一种有效确定权重的方法[17].
灰色关联度是基于各因素之间发展趋势的相似性和差异性,为衡量各因素之间的关联程度提供一种定量的度量.样本量多少、有无规律它都同样适用,而且计算量小,非常方便,并且量化结果与定性分析结果之间不会出现不一致的情况.定义关联系数为
式中:ρ为分辨系数,取0.5;min min 是两级最小差,max max 是两级最大差;x0k代表第k个时刻光伏功率序列的值,xik表示第k个时刻各个影响因素的值.
具体计算过程如下:
1)原始数据归一化处理.
2)求绝对差值矩阵.将高频分量、低频分量和复合天气因素与原始功率序列相应的元素做差后取绝对值,形成绝对差值矩阵.
3)求矩阵关联系数.
式中:Δmin与Δmax分别为绝对差值矩阵Δ的最小值与最大值.
4)计算关联度.根据关联系数确定关联度,即
式中:ri表示第i个影响因素与功率的关联度.
2.2 相似日的选取
首先,通过斯皮尔曼相关系数得到各天气因素与功率的相关系数,将相关系数最大的因素通过VMD 分解成多个分量.其次,熵值表示序列的复杂程度,熵值越高代表序列越复杂,熵值越低代表序列越紧凑[18].本文使用排列熵对最大影响因素分解的分量进行划分,并将熵值大于0.6 的划分为高频分量,熵值小于0.6 的划分为低频分量,将剩余天气因素组合在一起构成复合天气因素.
考虑高频分量、低频分量和复合天气因素对原始功率的影响程度不同,计算各因素与功率的灰色关联度,对影响功率更大的因素赋予更大的权重.将各个影响因素的结果进行加权得到最终结果.
由式(22)求出m个影响因素与原始功率之间的关联度r1,r2,…,rm,确定权重为
式中w1,w2,w3为权重,HFi为高频分量,LFi为低频分量,CIFi为复合天气因素,Ri为综合评价指数值.
计算出综合评价指标Ri的值,并将Ri由大到小排序得到相似日;本文选取前20 天的数据作为相似日数据集.
3 光伏功率预测模型
3.1 NGO优化BiGRU模型
为提升BiGRU 模型的预测精度,本文利用北方苍鹰算法对BiGRU 的超参数进行优化.考虑到学习率过低会使学习速度太慢,而学习率过高又很难收敛,因此采用LearningRateScheduler 调度器,对学习率进行动态设置,学习率设置在[0.001,0.01].NGO算法同时优化了BiGRU 的神经元个数和batch_size,神经元个数设置在[10,100],batch_size 设置在[20,50].相关参数具体设置如表2 所示,优化流程如图4所示.对预测模型的基体优化过程如下:

表2 参数设置Tab.2 Parameter settings
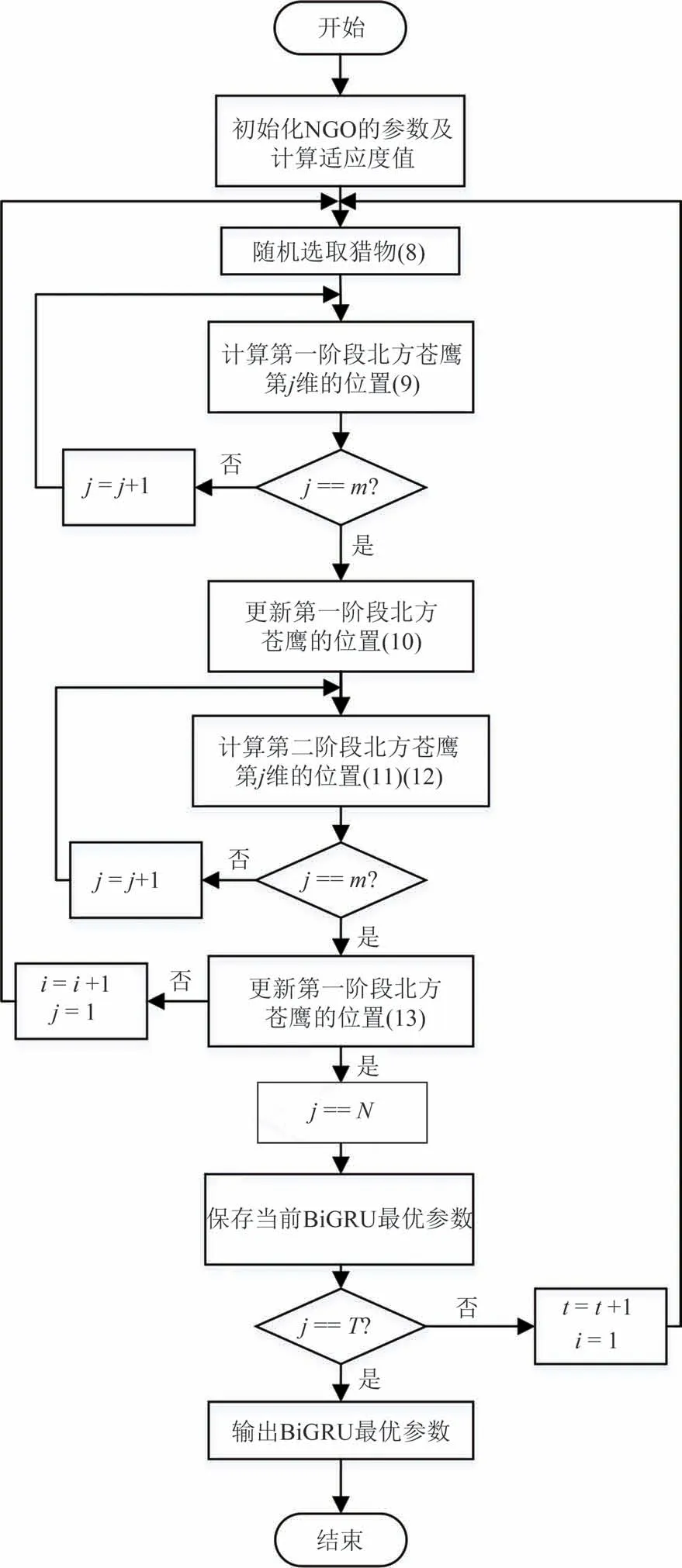
图4 NGO优化BiGRU流程图Fig.4 NGO optimization BiGRU flowchart
1)初始化北方苍鹰的种群数目和位置,并计算北方苍鹰的目标函数值;
2)首先对搜索空间进行全局搜索,确定最优区域.随机选取猎物,通过式(12)计算猎物的位置,再由式(13)计算第一阶段北方苍鹰的位置;
3)判断北方苍鹰是否攻击猎物.若没有攻击则由式(13)继续更新北方苍鹰的位置;若对猎物发动攻击则由式(14)更新北方苍鹰的位置并跳出循环,进入第二阶段;
4)第二阶段北方苍鹰对猎物进行追逐和抓捕.由式(15)和式(16)计算第二阶段北方苍鹰的位置;
5)判断是否抓获猎物,若没有抓获猎物,则继续更新第二阶段北方苍鹰的位置;若抓获猎物,则输出北方苍鹰位置,即输出最优参数.
3.2 基于相似日选取和VMD-NGO-BiGRU 的短期光伏功率预测
基于相似日选取和VMD-NGO-BiGRU 的短期光伏发电功率预测流程如图5所示,具体步骤如下:

图5 预测模型流程图Fig.5 Flow chart of this prediction model
1)利用斯皮尔曼相关系数选出主要的气象因素;
2)VMD 分解原始功率和影响最大的气象因素,并将影响最大的气象因素的分量通过排列熵划分为高频分量(HF)和低频分量(LF);
3)将其它较不重要的气象因素表示为复合气象因子(CIF),构建新的综合评价指数,计算各因素与功率之间的灰色关联度ri,得到权重wi,使用 式(24)计算Ri的值,并将Ri由大到小排序得到相似日;
4)将分解后的原始功率序列的子分量分别输入经NGO优化的BiGRU网络模型中进行训练;
5)将各分量的预测结果进行叠加重构,得到最终预测结果.
为验证本文所提方法的有效性,采用三种评价指标对预测模型进行评价.分别是均方根误差(root mean square error,RMSE)、平均绝对误差(mean absolute error,MAE)和平均绝对百分比误差(mean absolute percentage Error,MAPE),具体公式如下:
4 算例分析
本文选取2022 年江苏某光伏电站一整年的数据进行分析.将天气划分为三种天气类型:晴天、阴天和雨天.每种天气类型都由综合评价指数选取前20 天的相似日作为数据集,其中前18 天作为训练数据,剩余2 天作为测试数据.每日选取数据时间为 7∶00~18∶45,每隔15 min 记录一次,一天共有48 条数据.为验证不同天气类型下相似日的效果,选取2022 年8 月26 日(晴天)、2022 年8 月29 日(阴天)和2022 年9 月20 日(雨天)三天为待预测日进行实例分析.
4.1 VMD分解结果
VMD 有两个重要的参数分解个数k和惩罚因子α,分解个数过大会造成过拟合,分解个数过小不能提取出有效信息,因此分解个数的选取要适中.以功率分解为例,如表3 所示,观察中心频率可得,当k=6时IMF3 和IMF4 比较相近;当k=7 时IMF4 和IMF5 比较相近,由于中心频率相近会产生模态混叠现象,不利于信息的提取,因此分解个数为5 比较适当.同理可得总辐射分解个数应为6.VMD分解相似日功率和总辐射的结果分别如图6和图7所示.

表3 不同k值下分解相似日功率的中心频率Tab.3 The center frequency of decomposed similar daily power under different k values
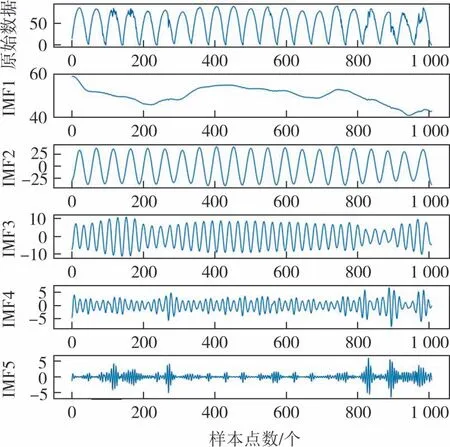
图6 VMD分解相似日功率Fig.6 VMD decomposition similar daily power
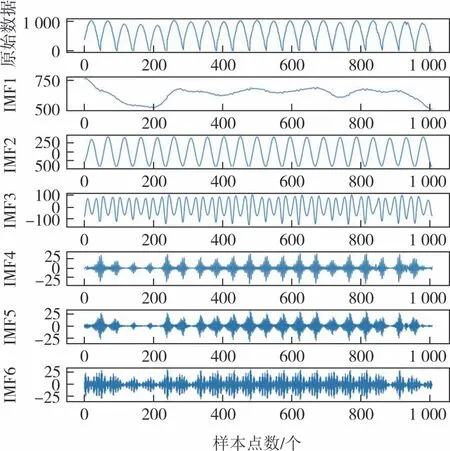
图7 VMD分解总辐射Fig.7 VMD decomposition total radiation
4.2 相似日的选取结果
重构VMD 分解总辐射的分量,将熵值小于0.6的划分为低频分量,大于0.6 的划分为高频分量.由表4 可知,将IMF2 和IMF3 重构划分为低频分量,剩余分量重构为高频分量.其余天气影响因素则通过归一化处理,加和求平均重构为复合天气因素.

表4 VMD分解总辐射的分量熵值Tab.4 Component entropy value of VMD decomposition total radiation
本文旨在通过计算灰色关联度的值进行权重的分配,由式(22)计算出低频分量、高频分量和复合天气因素与功率的灰色关联度,如表5 所示.由式(23)计算出各影响因素的权重如表6所示.

表6 各影响因素的权重Tab.6 Weights of various influencing factors
以2022 年8 月26 日(晴天)为例,通过构建新的综合评价指数Ri,由式(24)计算出Ri的值并以降序排列的方式,筛选出前20 天的相似日,前20 天相似日的综合评价指数值如表7所示.
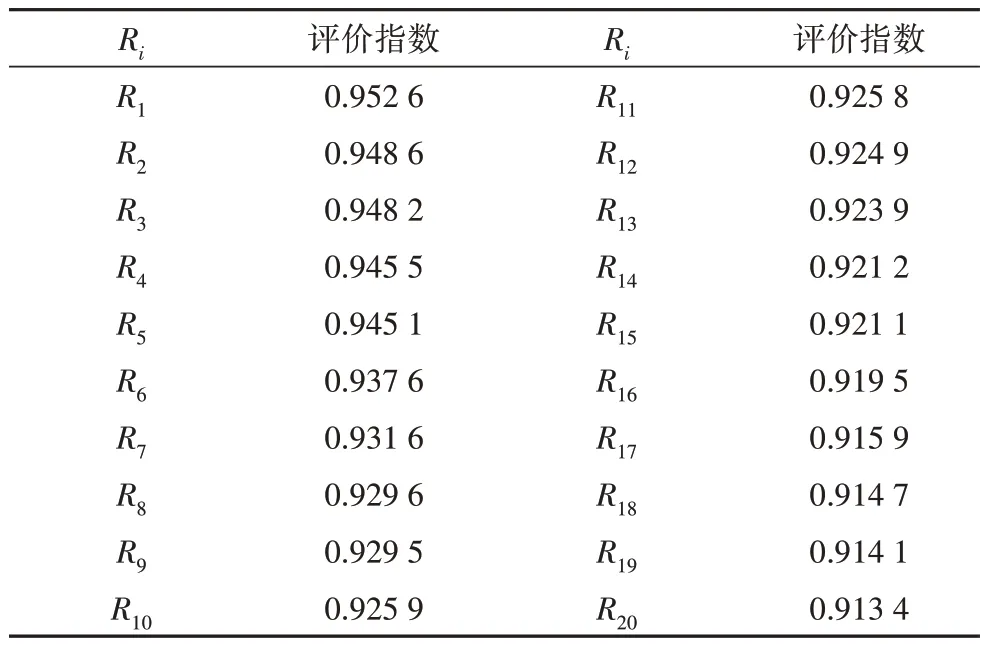
表7 相似日综合评价指数Tab.7 Comprehensive evaluation index for similar days
为了验证选取的相似日与待预测日是否具有相似性,绘制如图8 所示的20 个相似日与待预测日的功率趋势图.图中虚线代表的是待预测日的功率曲线,由图可知所选取的20 个相似日功率曲线的趋势与待预测日基本保持一致,验证了所提方法选取相似日的有效性.

图8 相似日与待预测日的功率趋势图Fig.8 Power trend graph of similar day and day to be predicted
4.3 优化算法结果对比
为检验NGO 优化算法的性能,将NGO 优化算法与粒子群算法(Particle Swarm Algorithm,PSO)和鲸鱼优化算法(Whale Optimization Algorithm,WOA)进行对比.设置PSO 个体最优系数c1=1.0,全局最优系数c2=1.5,惯性系数w=0.8.初始化设置三种优化算法的种群数量为30,迭代次数设置为50.从图9 可以看出,PSO 算法虽然收敛速度相对较快,但在三种优化算法中,适应度值最大,寻优能力最差;WOA 算法是三种优化算法中收敛速度最慢的,适应度值相对于PSO 较小,寻优能力次之;NGO 算法在三种优化算法中收敛速度是最快的,适应度值也是最小的,寻优能力最强.

图9 优化算法迭代图Fig.9 Optimization algorithm iteration diagram
4.4 整体预测结果对比
本文从单一模型和组合模型两个方向进行实例验证,逐步验证在不同天气类型下所提方法的有效性.选用的数据集是通过综合评价指数选取的与待预测日相似的前20天的数据.
在单一模型预测中,选取极限学习机(Extreme Learning Machine,ELM)、BP 神经网络(Back Propagation,BP)、支持向量回归(Support Vector Regression,SVR)、LSTM 和BiGRU 五种网络模型进行对比试验.由图10 可知,在不同天气类型下,BiGRU 模型预测值与真实值的拟合程度更好,三种误差均是最小的.由表8 可知,在晴天情况下,BiGRU 模型的RMSE、MAE 和MAPE 比LSTM 分别提升了12.29%、19.93%和2.11%;在阴天情况下,BiGRU 模型的RMSE、MAE和MAPE 比LSTM 分别提升了6.08%、13.78% 和10.47%;在雨天情况下,BiGRU 模型的RMSE、MAE和MAPE 比LSTM 分别提升了6.37%、29.02% 和19.31%.说明筛选过相似日后,使用BiGRU 模型进行功率预测效果会更好.

表8 单一模型评价指标Tab.8 Single model evaluation index

图10 单一模型不同天气类型下预测结果对比Fig.10 Comparison of forecast results of single model under different weather types
在组合模型预测中,选取NGO-BiGRU(方法1)与本文方法进行对比,证明对原始功率分解能够更大限度地提升模型的预测精度;为验证NGO 算法的优越性,将本文方法与VMD-PSO-BiGRU(方法2)、VMD-WOA-BiGRU(方法3)进行对比.
晴天时,由图11(a)可知,晴天时的光伏功率波动比较小,各方法预测曲线与真实功率曲线的拟合程度都比较好.从图12(a)可以看出,本文方法的三种误差最小,准确度最高.为了更加清晰的展示本文方法的精度,由表9 可知,在晴天情况下,经过NGO优化的BiGRU 比单一模型BiGRU 的RMSE、MAE 和MAPE 分别提升了2.27%、6.31% 和43.05%,说明NGO 优化BiGRU 模型是有一定效果的;本文方法比未经过VMD 分解的方法1 的RMSE、MAE 和MAPE分别提升了11.56%、6.31%和38.91%,说明分解原始功率能够提取更多重要信息;本文方法与方法2 相比RMSE、MAE 和MAPE 分别提升了5.5%、2.13%和11.03%,说明NGO 算法优化BiGRU 模型要优于PSO算法;本文方法与方法3 相比RMSE、MAE 和MAPE分别提升了3.11%、2.37%和7.40%.

表9 组合模型误差指标Tab.9 Combined model error indicator

图11 组合模型不同天气类型下预测结果对比Fig.11 Comparison of prediction results of combined models under different weather types

图12 组合模型不同天气类型下评价指标Fig.12 Evaluation indicators of combined models under different weather types
阴天时,由图11(b)可知,阴天时的光伏功率波动略大,各方法的预测曲线与真实功率曲线的拟合程度相较于晴天略差.从图12(b)可以看出,虽然本文所提方法的三种误差仍是最小的,但是相对于晴天来说误差有所增大,这是由于光伏功率的发电受到天气因素的影响.由表9 可知,在阴天情况下,经过NGO 优化的BiGRU 比单一模型BiGRU的RMSE、MAE和MAPE分别提升了4.12%、8.79%和14.92%;本文所提方法比未经过VMD 分解的方法1的RMSE、MAE 和MAPE 分别提升了36.16%、21.46%和31.83%;本文方法与方法2 相比RMSE、MAE 和MAPE 分别提升了8.99%、8.32%和11.05%;本文方法与方法3 相比RMSE、MAE 和MAPE 分别提升了2.88%、2.19%和9.32%.
雨天时,由图11(c)可知,雨天时的光伏功率波动较为剧烈,各方法预测曲线与真实功率曲线的拟合程度也相对较差.从图12(c)可以看出,在误差评价指标中,本文所提方法的误差仍是最低的,但整体预测效果相较于晴天和阴天的预测效果略差一些.由表9可知,在雨天情况下,经过NGO 优化的BiGRU比单一模型BiGRU 的RMSE、MAE 和MAPE 分别提升了23.70%、13.12%和41.52%;本文方法比方法1的RMSE、MAE 和MAPE 分别提升了18.65%、12.91%和19.49%;本文方法与方法2 相比RMSE、MAE 和MAPE 分别提升了8.10%、8.99%和8.19%;本文方法与方法3 相 比RMSE、MAE 和MAPE 分别提升了5.99%、7.02%和7.38%.
通过实例分析,验证了在各类天气类型下,组合模型的预测效果比单一模型的预测效果要好.通过BiGRU 与方法1 对比可知,经过NGO 优化算法选取的参数进行功率预测,结果更为准确;通过本文方法与方法1 对比可知,功率经过分解的模型预测精度要比未分解的精度高.将本文方法与方法2 进行对比,可知NGO 优化算法优化BiGRU 的参数是优于PSO 和WOA 优化算法的。在晴天、阴天和雨天三种天气类型下,本文所提方法的MAPE 分别为1.8925%、2.7190%和4.1671%,均在5%以内,由此说明,经过NGO 优化的BiGRU 模型有更强的鲁棒性和预测性能.
为验证所提选取相似日方法对模型的预测精度是有所提升的,以2022 年8 月26 日(晴天)的数据为例,将本文筛选相似日方法与未筛选相似日和用模糊C 均值聚类(Fuzzy C-Means Algorithm,FCM)筛选相似日的方法进行对比.未筛选相似日的数据集为2022年江苏某光伏电站一整年中晴天天气类型的前20 天的数据.FCM 选取相似日的数据集为筛选出的数据集中前20 天的数据.三者均通过VMD-NGOBiGRU 模型进行预测,未筛选相似日(No_Similar_Day)、FCM 筛选相似日(FCM_ Similar_Day)和本文方法筛选相似日(Similar_Day)的预测结果如图13所示,评价指标如表10所示.由表10可知,FCM 筛选相似日比未筛选相似日的RMSE 提升了8.52%,MAE提升了10.8%,MAPE提升了2.19%;本文筛选相似日方法比FCM 筛选相似日的RMSE 提升了14.96%,MAE 提升了9.99%,MAPE 提升了3.04%.由此可知,FCM 选取相似日相对于未筛选相似日的数据来说,预测结果精度有所提升;相较于FCM选取相似日,本文所提筛选相似日的方法对模型的预测精度有更大的提升.

表10 未筛选相似日和筛选相似日误差指标Tab.10 Unscreened similar days and screened similar day error indicators

图13 未筛选相似日预测结果Fig.13 Unscreened similar day prediction results
5 结语
针对不同天气条件下,模型的预测性能和鲁棒性仍然存在不足的问题,本文提出了一种基于相似日选取和北方苍鹰算法优化双向门控循环单元的短期光伏功率预测模型,并得到如下结论:
1)本文构建的新的筛选相似日的评价指标筛选出的相似日相较于传统聚类方法更加适合待预测日,对模型预测精度有一定提升.
2)NGO 算法与PSO 优化算法相比具有更强的寻优性能,可以为BiGRU获取更优参数解,提高了模型的预测性能.
3)本文模型在不同天气影响下,对应的RMSE、MAE 和MAPE 均有较大幅度提升,预测误差值也比较小,充分凸显了该模型良好的预测精度.
仿真结果表明,经本文构建的筛选相似日的评价指标有效地筛选出了相似日数据集,通过模型进行训练,在不同天气类型下的误差评价指标均优于其他模型,具有良好的适应性.

