基于串并对称式液冷流道的锂电池散热分析

刘霏霏 ，虞帮强 ，秦武 ，程贤福 ，曾建邦

（1.华东交通大学 机电与车辆工程学院，江西 南昌 330013；2.华东交通大学 载运工具与装备教育部重点实验室，江西 南昌 330013）

随着电动汽车的日益发展，动力电池的热安全问题逐渐引起广泛关注，而工作温度显著影响电池的性能［1］.对于锂离子动力电池，其最佳工作温度为25～40 ℃，同时需保证小于5 ℃的温差［2］.电池模组在大电流充放电下运行时，由于焦耳热和内部化学反应而产生大量热量，会导致局部热量积累，致使电池模组内部产生较大的温差和严重的温升，并削弱电池的工作性能，加速电池老化，缩短电池寿命［3］.在严重的情况下，将产生热失控事故［4］.

国内外学者针对锂离子液冷散热系统设计方面做了大量研究.Monika 等［5］比较了蛇形、U 形、直形、南瓜形、螺旋形和六边形结构液冷板对电池温度的影响，发现蛇形和六边形结构的液冷板可以显著提高电池的温度均匀性.Lu 等［6］分析相邻特斯拉阀之间的角度、相邻特斯拉阀之间的距离、相邻通道之间的距离以及冷却剂入口速度对电池温度的影响.结果表明，角度为120°，特斯拉阀距离为23.1 mm，通道距离为28 mm，入口速度为0.83 m·s-1的反向特斯拉阀式通道液冷板在热交换性能和能耗之间具有良好的平衡.Zhang 等［7］分析了冷却通道的布置形式，出入口数量以及结构参数对电池温度的影响.与原始模型相比，电池的平均温度和液冷板的压降分别降低了1.17 ℃和22.14 Pa.Siruvuri 等［8］分析了体积流量、流向和接触面积对电池散热的影响.结果表明，在0.25×10-6m·s-1和1.6×10-6m·s-1的冷却流量下，电池5C倍率放电的最高温度分别为319.31 K 和316.93 K.与顺流相比，逆流能够将电池的最高温度降低2.77 K.Gao 等［9］对比了三进三出、六进六出、三进六出的液冷通道，在入口流量为360 mL/min时，与三进三出对比，使用六进六出和三进六出的液冷通道能够将电池最大温差降低69.4%和41.3%.Ran等［10］设计了一种八进四出的树形通道，研究了冷却水温度和电池放电倍率对电池模组的散热效果.结果表明，该液冷通道可将电池模组的最高温度、最大温差和电池内最大温度梯度分别维持在40 ℃、1 ℃和5 ℃以下.Guo 等［11］比较了一进一出的蛇形流道、两进两出的蛇形流道和四进一出的X 型流道，研究发现，与一进一出的蛇形流道对比，两进两出的蛇形流道和四进一出的X 型通道分别将电池的最高温度降低了4.1 ℃和5.8 ℃.

针对锂离子电池均温性差和液冷系统能耗高问题，以方形三元锂电池作为研究对象，在单体模型验证的基础上，设计了5 种流道的液冷散热结构，仿真分析了在5 种流道形状下电池单体间的温差，在优选串并对称式液冷流道形状的基础上，同时保证铝板的总质量不变，调节铝板厚度的分布，讨论了液冷系统启动时间，进一步优化了冷却系统的温度均匀性，得出最佳优化方案.

1 模型建立

1.1 锂离子电池热模型

锂离子电池的发热主要包括四个部分：反应热、极化热、焦耳热和副反应热.通常，副反应热因其比例较小而被忽略［12］.方程式如下［13］.

式中：V为电池体积，m3；I为电池电流，A；R为电池总内阻，mΩ；T为电池温度，K；UOCV为电池开路电压，V；dUOCV/dT表示电池的熵系数，V·K-1，其是电池荷电状态SSOC（SOC的值）的函数［14］.

考虑到锂离子电池内部结构复杂，由正极、负极、铝箔层和隔膜组成.在进行数值计算时，假设电池内部材料均一，同一方向导热系数相同；电池的密度、比热、导热系数不随温度变化；热量均匀地在电池内部产生.基于上述假设建立如下电池热模型.

式中：ρ为电池的密度，kg·m-3；λ为电池导热系数，W ·(m · K)-1；cp为电池比热容，J ·(kg · K)-1；q为电池的平均生热率，W·m-3；T为温度，℃；t为电池放电时间，s.

1.2 控制方程

对于一个电池单体，考虑到热量的产生，热传递由电池内部传递到表面，并与液冷板表面进行热传导.对于液冷板，不考虑其自身的发热，其内部冷却液采用水作为冷却介质，电池与液冷板壳体之间存在导热，而液冷板与冷却水之间存在对流换热，相应的质量、动量、能量守恒方程如下.

式中：ρw代表液态水的密度，kg·m-3；c为比热容，J ·(kg · K)-1；v为速度矢量，m·s-1；k为液体的导热系数，W ·(m · K)-1，P代表压强，Pa.

1.3 边界条件

求解控制方程的边界条件如下，设置冷却液的入口温度为25 ℃，入口为速度入口，出口为压力出口，冷却液的动力黏度为0.001 003 Pa·s.流动状态由雷诺数决定，计算方程如下.

式中：v为流速，m·s-1；D为等效直径，m；μ为动力黏度，Pa·s.入口流速为0.1～0.16 m·s-1，对应的雷诺数为334～534，小于2 300，故选择层流模型.

液冷系统的能耗计算如下［15］.

式中：W为液冷系统的能耗，J；P为压力，Pa；Q为冷却液的质量流量，kg/s.

1.4 网格无关性验证

网格划分和数值求解是在商业软件ANSYS Fluent 软件中完成的.选用的网格类型为Poly-Hexcore网格，设置入口流速为0.13 m·s-1，入出口温度和环境温度均为25 ℃.图1 是网格无关性验证结果，当网格数量在1 240 420到2 499 079之间变化时，电池模组的最高温度Tmax保持在一个相对稳定的水平，说明仿真结果与网格数量无关.在保证数值计算精度和计算负荷前提下，本文选择1 240 420的网格数.

图1 网格无关性验证结果Fig.1 Mesh independence results

2 锂离子电池热特性实验

2.1 研究对象

以某3.75 V5.8 Ah 方形三元锂电池单体作为研究对象，电池单体参数如表1所示.

表1 电池单体参数Tab.1 Battery cell parameters

2.2 电池热特性实验

为了获得锂离子电池的发热和温度分布，需要进行电池热特性实验，包括混合功率脉冲特性测试（Hybrid PulsePower Characteristic，HPPC）和温升测试，为锂离子电池热模型的建立和验证提供数据，进而用于电池热模型的验证.

2.2.1 实验设备

实验平台由SC-80-CB-2 型恒温恒湿箱，CE-6002n-30V100A-H 型新威电池测试仪，控制电脑，K型热电偶和CA-4008-1U-VT-TX 型数据记录仪搭建，如图2 所示.恒温恒湿箱，东莞市三木科技有限公司产，控制电池测试的环境温度.电池测试仪，深圳市新威电子有限公司产，对电池进行充/放电测试.计算机记录电池的电压、电流和容量等数据.数据记录仪，深圳市新威电子有限公司产，连接热电偶检测电池的表面温度.电池测试仪的电流精度达到 0.1%RD±0.1%FS，恒温箱的可测温度为-20～150 ℃，温度误差在±0.2 ℃以内，热电偶的测温范围为-200～350 ℃，精度为 ±1.5 ℃.将电池放置在25 ℃下恒温箱内，先以恒流恒压充电，将充满电的电池在恒温箱中搁置2 h，再对其进行HPPC 和温升测试并记录其数据.

图2 电池热特性实验平台Fig.2 Experimental platform for thermal characteristics of battery

2.2.2 测试结果

电池以1C放电10 s，搁置40 s 后，再以0.75C充电10 s，形成一个脉冲循环，即HPPC 测试，然后再以1C放10%的SSOC，继续下一个脉冲循环，直至SSOC为0.图3是电池总内阻随Ssoc变化图.当电池处于低SSOC范围（SSOC＜20%）时，电池总内阻随SSOC增加而减小.当SSOC处在20%～70%时，总内阻随SSOC增加而增加.当电池处于高SSOC范围（SSOC＞70%）时，电池总内阻几乎不变.为了得到更精确的模型，采用最小二乘法，对25 ℃放电的总内阻进行多项式拟合，得到图3的拟合曲线及以式（8），输入到编译UDF 的生热模型中.

图3 电池总内阻随SSOC变化图Fig.3 Variation of total internal resistance of battery varying with SSOC

图4 为电池热电偶的布置图.4 个热电偶分别连接到电池的正极（T1）、负极（T2）、表面中心（T3）和电池负极底部（T4）.图5显示了电池在2.5C时的电池表面温度.电池的最高温度Tmax为43.1 ℃，最大温差ΔTmax为4.1 ℃.根据图3 的SSOC变化曲线可知，在放电初期，电池处于高SSOC范围，电池的内阻较大，电池发热量较大.随着温度的升高，电池的内阻降低，电池的发热量降低.当电池的SSOC降低到0.2以下时，电池的内阻升高，电池的发热量上升.因此，电池的温度曲线先上升再平缓后又上升，如图5 所示.由于在放电初期，电池内部的化学反应较慢，此时电池的正负极呈现一定的电阻，当电流通过时，电池正负极处会产生相应的焦耳热，因此，电池的正负极温度略高于电池中心表面和负极底部温度.随着放电深度的增大，电池内部电化学反应剧烈，产生大量的热，此时电池表面的中心温度将高于其他位置的温度.

图4 电池热电偶布置图Fig.4 Layout of thermocouple for battery

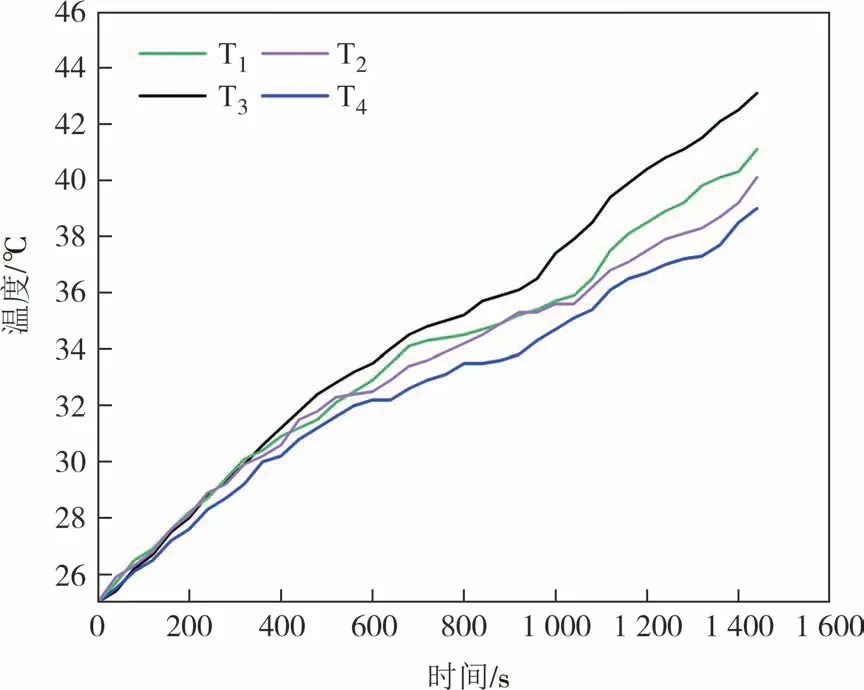
图5 2.5C放电时电池表面温升Fig.5 Temperature rise of battery surface during 2.5C discharge

2.2.3 仿真结果验证

图6 为2.5C放电结束时电池表面温度云图.由图6 可知，电池表面中心的温度最高，温度次高的区域在电池正极附近，且电池温度由中间向边缘逐级递减，这与温升测试下热电偶的测量结果基本一致.仿真监测了电池表面中心点T3的温度和电池负极底部T4的温度，并与实验数据进行了对比，如图7 所示，2.5C放电结束时，仿真监测电池表面中心点T3和电池负极底部T4的温度分别为42.2 ℃和40.1 ℃，而实验测得的温度分别为43.1 ℃和39.5 ℃，电池在整个放电过程的最大相对误差均在5%以内，说明所建立的电池热模型具有较高的准确性，可用于电池模组液冷散热的研究.

图6 2.5C放电结束时电池表面温度云图Fig.6 Nephogram of battery surface temperature at the end of 2.5C discharge

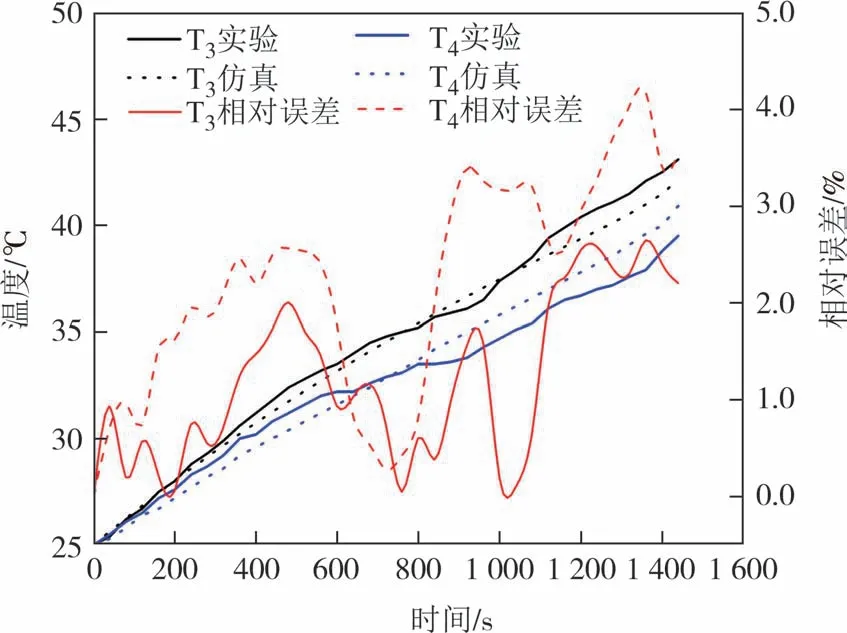
图7 电池表面温度仿真和实验对比Fig.7 Simulation and experimental comparison of battery surface temperature

3 冷却系统结构建立

图8是液冷板和电池模组的几何模型.由图8（a）可知，电池模组由10 个电池单体串联而成，沿x轴正方向，分别命名为电池单体1 至电池单体10，每相邻两个电池单体间放入一块铝板（长×宽=122 mm× 88 mm），且电池与铝板在y-z平面紧密接触，初步设定铝板的厚度为2 mm.两个液冷板沿z方向分别置于电池模组的两端，且铝板与液冷板表面接触，忽略两者间的接触热阻.由图8（b）可知，冷却液的入口和出口分别布置在液冷板沿z方向并且入口夹角和出口夹角分别为3°，其入口和出口由10 个通道并行连接，相邻通道之间的间距相等，沿z轴方向流道的厚度为2 mm，其他参数如图8 所示.考虑到经济性和导热性，冷却液采用25 ℃的水，液冷板采用铝.各材料的热物性参数如表2 所示.

表2 材料热物性参数Tab.2 Thermophysical parameters of materials

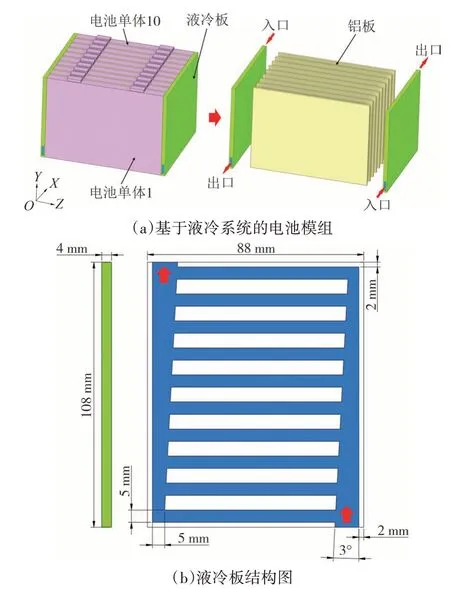
图8 液冷板和电池模组的几何模型Fig.8 Geometric model of liquid cooling plate and battery module

4 仿真结果与分析

4.1 方案分析

在初始流道S0（如图8 所示）的基础上，设计了5种方案的流道形状，设置流速v=0.13 m·s-1，流道S0和流道S2的入口流速为v，流道S1、流道S3及流道S4入口流速为v/2，如图9 所示.方案一即初始流道S0，10个通道并行连接的结构；方案二即流道S1，在初始流道S0基础上，将前三个通道并行连接，后两个通道并行连接，呈对称式布置结构；方案三即流道S2，将初始流道S0向左旋转90°布置，8个通道并行连接；方案四即流道S3，前四个通道两两并连；方案五即流道S4，前三个通道并行连接.考虑到结构的对称性，本文仅对电池单体1～5 进行分析，仿真结果如图10 所示.图10（a）是不同流道形状下各单体间的最高温度，从图中可知，5 种流道对电池单体间的最高温度影响均较小，其中流道S3各单体的最高温度最低.图10（b）是不同流道形状下的各个单体间的温差，可以观察到，流道S0中电池单体的ΔTmax为3.9 ℃，由流道S2可知，减少通道的数量会使得电池的Tmax和ΔTmax均升高，这是因为通道数量降低会导致液冷板和电池的接触面积减小，从而降低电池的换热效果.与初始流道S0对比，流道S1中电池单体的Tmax和ΔTmax均降低了，因此合理分配串并数量可以降低电池的温度，即设计了流道S3和S4，流道S3相比于S0，电池模组中电池单体的ΔTmax降低了15%，流道S4则降低了12.8%.

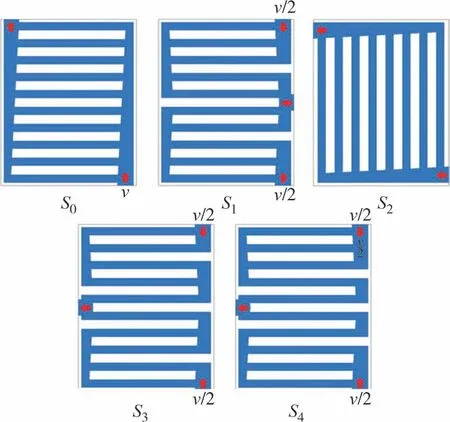
图9 5种流道形状示意图Fig.9 Schematic diagram of five flow channel shapes

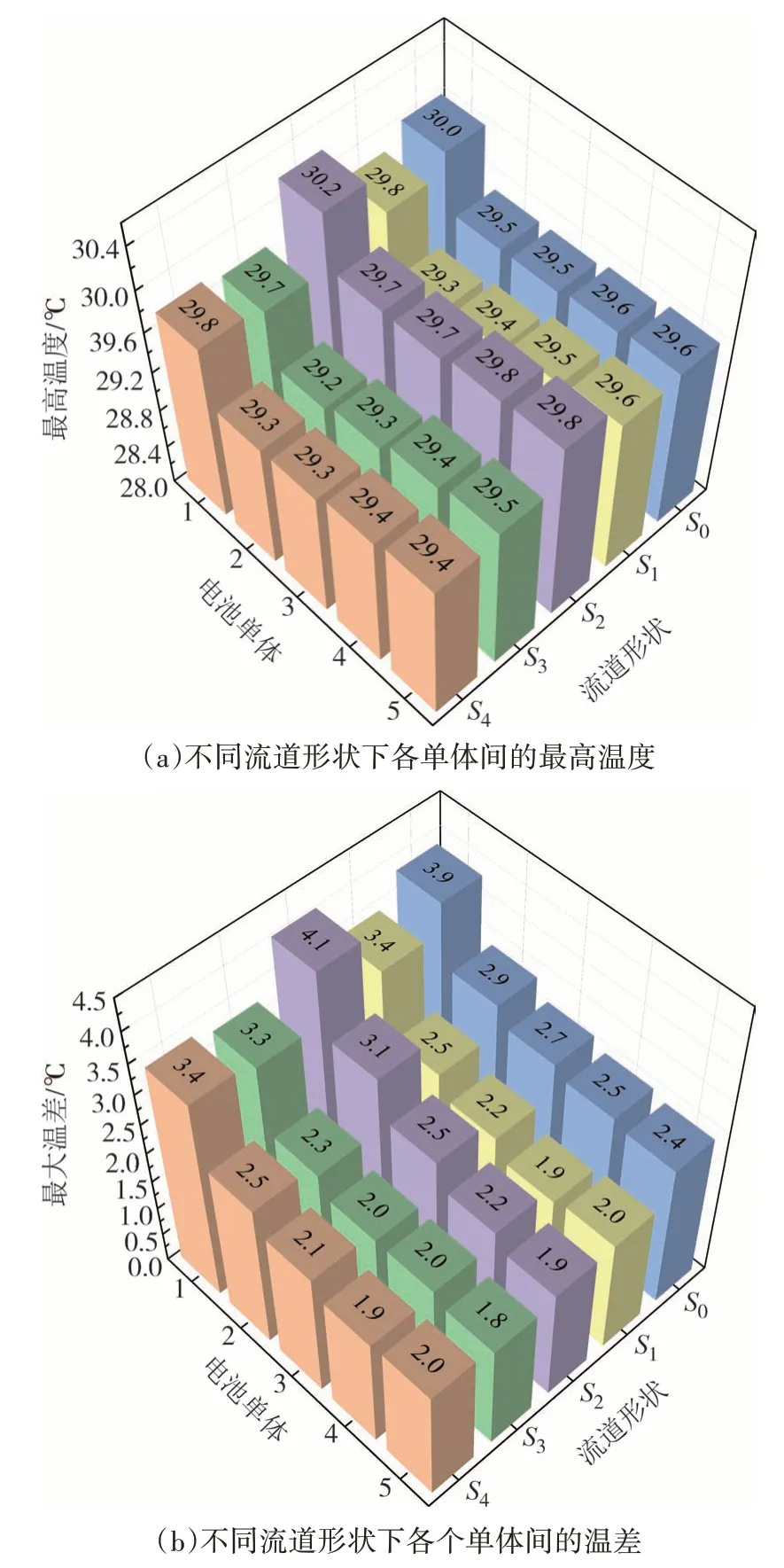
图10 不同流道电池单体的最高温度和最大温差Fig.10 Maximum temperature and maximum temperature difference of battery cells with different flow channels

图11为液冷板的温度云图，图中显示，流道S0和S2中液冷板的温度较高，热量无法及时散出，这是因为并行通道数量较多时，分配到各个通道的流量不均.沿流动方向的前两个通道和最后一个通道中的冷却液温度为25.4 ℃，处于较低的水平，说明此处的流速较高，而中间通道温度为26.1 ℃，冷却液流速较低，导致热量无法及时散出.与流道S0相比，流道S1中沿流动方向的前三个通道和后三个通道中的冷却液最低温度降低至25 ℃，改善了通道中流量不均的问题，但中间通道的最高温度为27.4 ℃，主要是因为冷却液在流动初期温度较低，随着流动时间的延长，冷却液的温度逐渐升高.流道S3中沿流动方向的前后两个通道最高温度为25.7 ℃，热量得以及时散出，但液冷板中间区域最高温度仍为27.4 ℃，且温度高于27.9 ℃的区域较大.相比于流道S3，流道S4中沿流动方向的前三个通道和后三个通道中液冷板的最高温度为26.7 ℃，液冷板高温区域明显减小.如图12和图13 所示，流道S4的压降最大，为157.9 Pa，流道S2的压降最小，为75.3 Pa.综上所述，在5种方案的流道形状下，方案四中流道S3的电池单体最高温度和最大温差均最小，压降为140.3 Pa.考虑到经济性，在后续的研究中，基于流道S3对电池单体的均温性能进一步优化.

图11 5种流道形状下液冷板的温度云图Fig.11 Temperature contour of the liquid cooling plate with five flow channel shapes

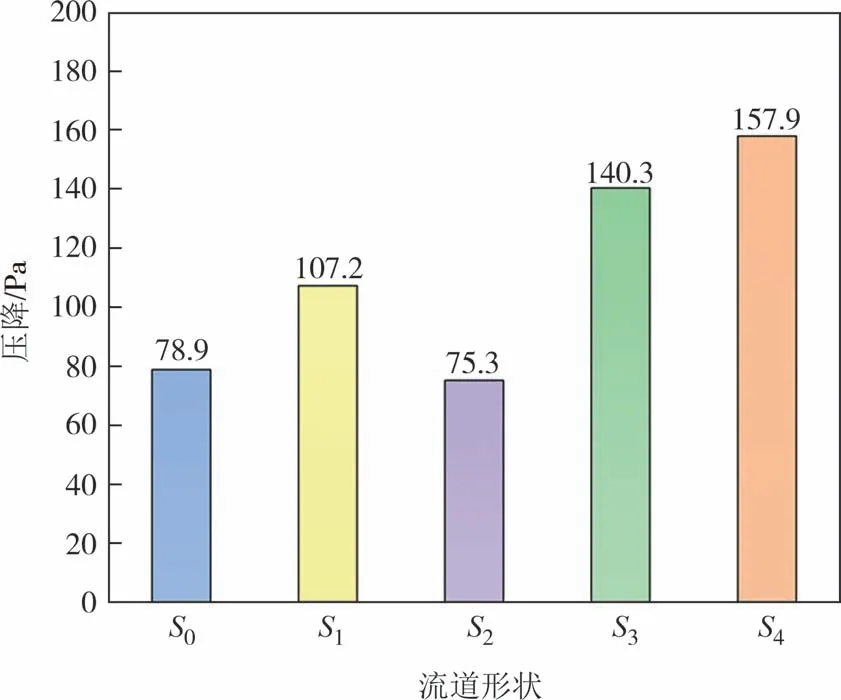
图12 5种流道形状下液冷板的压降Fig.12 Pressure drop of liquid cooling plate with five flow channel shapes

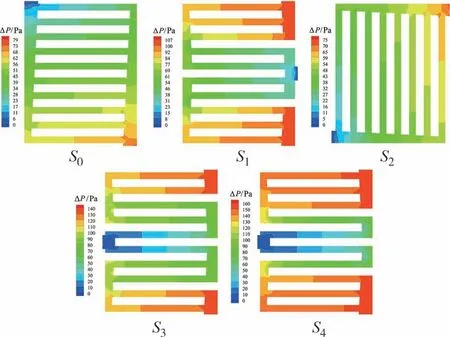
图13 5种流道形状下液冷板的压降云图Fig.13 Pressure drop cloud diagram with five flow channel shapes

4.2 影响因素分析

4.2.1 流速v

在基于液冷板的电池热管理系统中，铝板厚度组合h和液冷启动时间t的初始值分别为5 mm和0 s，流道形状使用最初的流道S0.图14 为不同流速下电池的冷却效果和压降，从图中可以看出，随着v的值从 0.01 m·s-1增加到 0.16 m·s-1，电池模组的最高温度Tmax下降了9.1 ℃，而模组的最大温差ΔTmax均在5 ℃内.v=0.01 m·s-1时，液冷板的流速较低，电池模组的热量无法及时散出，导致电池模组的Tmax较大，ΔTmax较大.电池的最高温度随着v的增加而降低，这是因为v的增加会导致努塞尔数增大，提高冷却液与液冷板之间的传热系数，电池散出的热量越多，液冷系统的冷却性能越好［16］.随着v的增加，流道中的冷却液流速加快，通道的压降ΔP将增加.当v增加到一定值时，Tmax和ΔTmax变化很小（趋于平缓），但压降仍然上升很快.因此，考虑到Tmax和ΔP的影响，液冷系统后续的研究是基于v=0.13 m·s-1这一条件的.

图14 流速对冷却效果和压降的影响Fig.14 Influence of flow rate on cooling effect and pressure drop

4.2.2 铝板厚度组合h

考虑到上述研究中单体间温差较大的原因主要是模组两端的电池散热不均.在保证液冷系统总质量不变的前提下，调整电池中铝板的厚度分布.所有铝板的初始厚度组合表示为h0，沿x轴正方向各铝板的厚度均为2 mm，h3和h4是分别在电池两端（x轴方向）增加了0.5 mm厚度的铝板，调整后的厚度分别定义为h1、h2、h3、h4，具体如下：

图15 是不同铝板厚度组合下电池模组的最大温差，从图中可知，模组使用铝板厚度组合h4，能够有效地降低电池模组的温差，降低了约12%，这是因为模组温度较高的区域主要是电池单体1 和电池单体10，增加铝板使其一侧对流换热的部分转换成导热，提高了换热强度，能够使热量有效散出.由图16可知，与初始铝板厚度组合h0相比，模组使用铝板厚度组合h4，电池单体的最高温度波动范围由0.5 ℃降低到0.1 ℃，提高了电池的均温性.图17 是h0和h4电池模组的温度云图，由图可知，模组温度较高的区域主要是电池单体1、单体5、单体6、单体10，而温度较低的区域是单体2、单体3、单体8、单体9，因此可以适当地缩减单体2、3，单体8、9 之间的铝板厚度，增加单体5、6 之间的铝板厚度，并在单体1、10 的两侧增加铝板，使其导热增加，从而降低电池模组的最高温度.因此，将基于h4进行后续的研究.

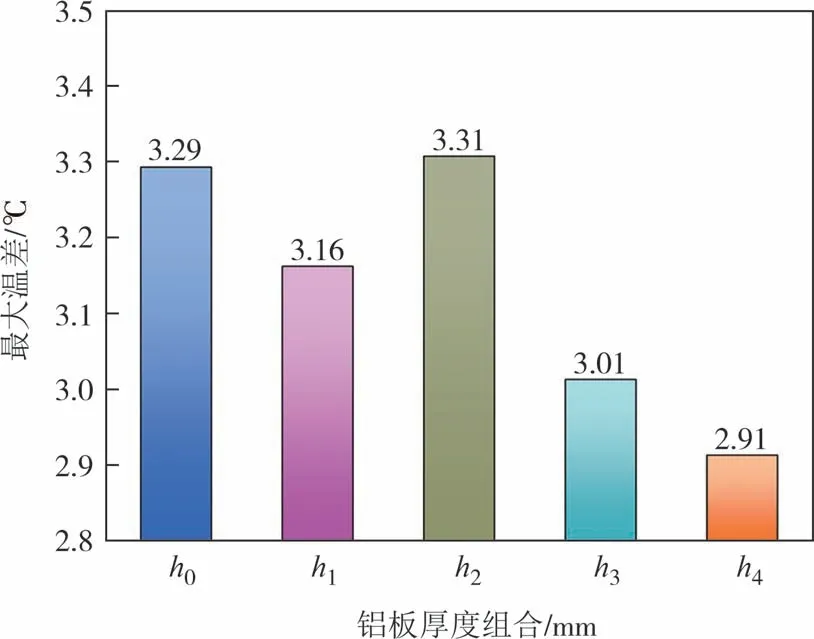
图15 不同铝板厚度组合下电池模组最大温差Fig.15 Maximum temperature difference of module with different combined aluminum plate thicknesses

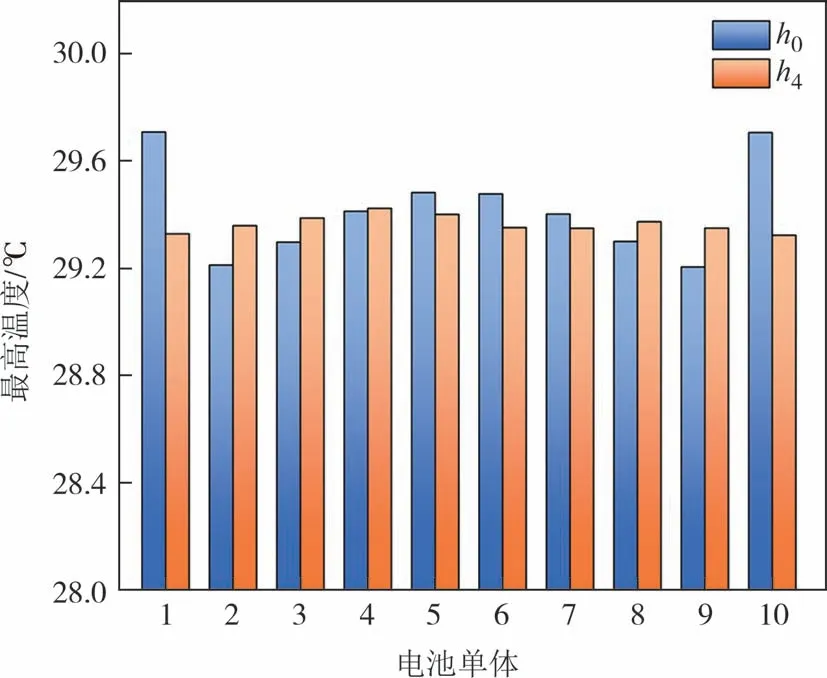
图16 h0和h4电池单体最高温度Fig.16 Maximum temperature of cells with h0 and h4

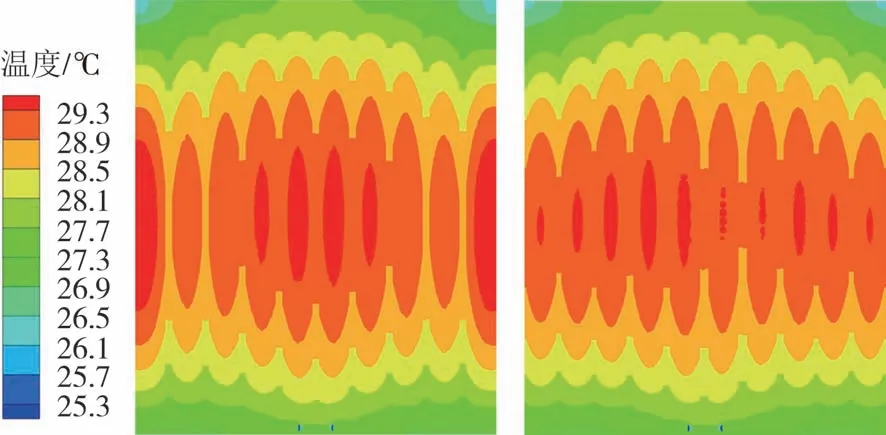
图17 h0和h4电池模组的温度云图Fig.17 Temperature nephogram of battery module with h0 and h4

4.2.3 液冷系统启动时间t

液体冷却的启动时间对于满足电池模块热管理的要求至关重要，因此在冷却过程中，适当选择冷却液启动时间有利于降低液冷系统的能耗.电池在2.5C放电下，设置液冷系统启动时间t为0 s、310 s、393 s、477 s、563 s 和651 s（对应电池模组的最高温度为25 ℃、29 ℃、30 ℃、31 ℃、32 ℃和33 ℃），此时液冷系统整体的工作时间分别为1 440 s、1 130 s、1 047 s、963 s、877 s和789 s.图18显示了电池模组在2.5C下电池模组的仿真结果，图18（a）显示，液冷系统一开始启动时，电池模组的温度一直处于较低的水平，随着t增加，电池模组的Tmax急剧上升.当t=563 s（此时电池最高温度为32 ℃）时启动液冷系统，整个放电过程电池模组的Tmax为32.2 ℃.图18（b）显示，Tmax随着t的延迟而增加，当t延迟到563 s 的操作时间（此时电池最高温度为32 ℃）时，ΔTmax在5.0 ℃内，整个放电过程电池的Tmax在32.5 ℃内.当t延迟到651 s 的操作时间，电池在整个放电过程中，电池模组的Tmax为5.2 ℃，超过了电池正常工作的范围.如图19所示，随着触发时间的延迟，液冷系统的能耗W在逐渐降低，当t=563 s 时启动液冷系统，此时液冷系统的W为167 J，这时电池的Tmax和ΔTmax均处于合适的范围内，相比于t=0 s 时启动液冷系统能够节约39%能耗成本，这意味着此时的启动时间对于电池模块冷却系统是最佳的.

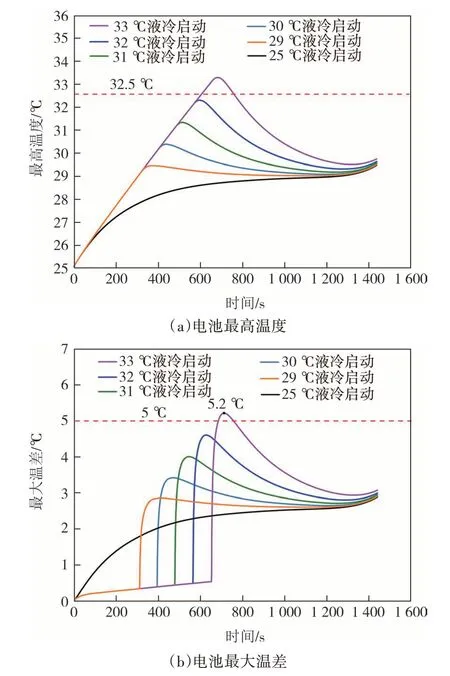
图18 不同启动时间对电池模组的冷却效果Fig.18 Cooling effect of different start-up time on battery module

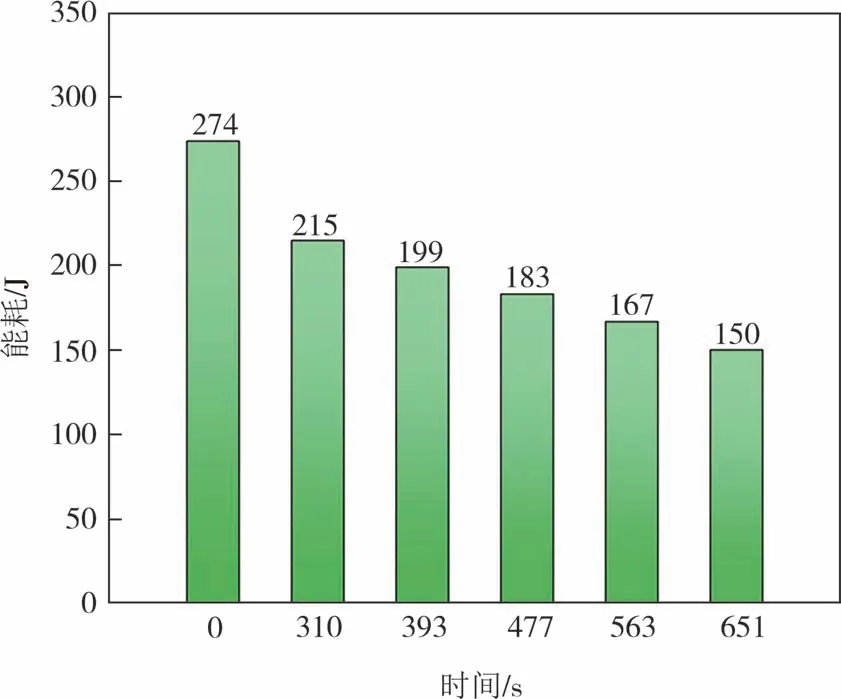
图19 不同触发时间液冷系统的能耗Fig.19 Energy consumption of liquid cooling system with different start-up time

5 结论

在单体模型验证的基础上，针对10 个电池单体串联的电池模组，设计了5 种流道的液冷散热结构，仿真分析了在5 种流道形状下电池单体间的温差，在优选串并对称式液冷流道形状的基础上，同时保证液冷系统总质量不变的前提下，分析了不同铝板厚度组合、不同液冷系统启动时间对电池均温性和液冷系统能耗的影响，优选出适用于电池模组的热管理方案，具体结论如下：

1）在不增加液冷系统质量的前提下，与方案一的初始流道S0对比，方案四的流道S3能够使液冷板通道中流量均匀性达到最佳，电池单体间的ΔTmax降低15%，提升了电池的均温性.因此，流道S3液冷散热系统具有更高的经济性和热均衡性.

2）电池的Tmax随着液冷流速的增加呈现先迅速减小后趋于平缓的趋势.流速增加，会导致努塞尔数增加，提高冷却液与液冷板之间的传热系数，电池散出的热量更多，液冷系统的冷却性能越好.但当流速增加到一定值时，随着v的增加，Tmax和ΔTmax变化很小，但压降仍然上升很快.

3）在保证液冷系统总质量不变的前提下，调整铝板厚度，能够大大地减低电池模组的ΔTmax，研究结果显示，与初始厚度组合h0对比，调整后的铝板厚度组合h4能够将电池模组的ΔTmax降低约12%.

4）电池在2.5C放电下，延迟液冷系统的启动时间至563 s，此时电池模组的Tmax和ΔTmax均处于最佳工作范围内，液冷系统的能耗为167 J，与未延迟液冷系统启动对比，能够节省液冷系统约39%能耗成本.