智能网联车辆节能自适应巡航控制研究

边有钢 ，何庆 ，李崇康 ，金馨 ，秦洪懋

（1.湖南大学 机械与运载工程学院，湖南 长沙 410082；2.湖南大学 无锡智能控制研究院，江苏 无锡 214115；3.山东省科学技术情报研究院，山东 济南 250101）

在世界范围内，公路交通的规模正迅速增长，为人员与货物的运输带来了极大便利.然而，一系列挑战随之而来，如交通事故日益频繁、交通拥堵更加严峻、能源消耗不断加速等［1］.作为缓解上述问题的重要方案之一，智能网联汽车（Intelligent Connected Vehicle，ICV）技术近年来获得了广泛研究与发展.通过搭载先进的传感器、控制器和执行器，并引入现代网络与通信技术，智能网联汽车不仅可以实现部分或完全自动驾驶，还可以利用车联网（Vehicle-to-Everything，V2X）实现协同工作.

通过V2V 与车-路（Vehicle-to-Infrastructure，V2I）通信，智能网联汽车可以获取附近车辆行驶状态、道路信息、交通流速和信号灯相位等信息，并基于这些丰富的交通状况信息进行更好的自车轨迹规划与控制［2-4］.

早期针对自适应巡航控制技术（Adaptive Cruise Control，ACC）的研究较多只考虑轨迹跟踪问题，即自身车辆根据前方领航车辆的状态信息计算自身控制输入，以保持期望的车辆间距［5］.常用的控制算法有PID 控 制［6-7］、滑模控 制（Sliding Mode Control，SMC）［8-9］、深度强化学习（Deep Reinforcement Learning，DRL）［10］和线性二次型调节器（Linear-Quadratic Regulator，LQR）［11-12］等.在轨迹跟踪方面，现有方法取得了良好的效果.

随着智能网联汽车技术的发展，汽车用户对ACC 技术的性能提出了更多期待，如较低的能源消耗率、较少的污染物排放和较好的乘坐舒适性等.为了实现多型性能目标的综合保证，基于优化的算法逐渐得到了更多关注.Lei 等［13］利用动态规划（Dynamic Programming，DP）算法，设计了以动力性、能耗和平顺性为目标的车辆驱动方案，但由于该方案采用了全局路径最优解，只能用于离线计算.为减小计算规模，Dib等［14］将已知全局路径分为多段短距离路径，以能源消耗量和通行时间为代价，使用动态规划设计了局部最优速度曲线求解器；作为改进，Dib等［15］通过分析汉密尔顿函数提出了一种可以实时应用的最优控制律.但动态规划方法通常基于离线道路信息求解最优轨迹，对环境的变化不能做出及时反馈，且计算负担较重，限制了实时应用.

模型预测控制（Model Predictive Control，MPC）是一种基于最优控制思想的算法，适合处理多输入多输出模型并允许施加状态及控制输入约束，可以考虑多种性能目标显式设计代价函数，且滚动求解优化问题，方便用于实时控制，在车辆工程领域得到了广泛研究与应用［16-18］.在基于MPC 方法进行节能ACC 算法设计的研究中，常见的方案是将车辆加速度作为经济评价指标，即将加速度绝对值作为最优控制问题的一项代价，使车辆以更平滑的速度行驶.但由于没有采用精确的显式能源消耗模型，上述方案的经济最优性通常较差［19］，基于能耗模型设计代价函数可以有效提高模型预测控制方法的经济最优性［20］.在对电动车辆（Electric Vehicles，EV）进行控制算法设计时，有研究人员考虑了驱动电机与动力电池的效率MAP 图，并将制动时的能量回收纳入优化问题，进一步提高了节能效果［21］.考虑到强非线性能耗模型造成的求解速度的降低，Schwickart 等［22］在分段线性模型的基础上，采用多个线性函数的极大值近似能耗，提高了ACC 算法的实时性.Weißmann等［23］基于能源消耗量及通行时间设计了代价函数，采用DP 离线求解全局路径的最优速度参考轨迹，并利用MPC 进行实时控制，通过结合DP 与MPC 提高了节能效果.考虑到真实行驶场景，一些研究采用更多的环境信息设计了优化问题，如道路坡度［24］、交通信号灯［25］和路段限速［26］等，提高了算法对不同路况的适应性.

自适应巡航控制通常使用传感器来获取前方车辆的状态信息，如毫米波雷达和激光雷达等，但是由于传感器的测量误差和噪声等因素的影响，所获取到的状态信息可能存在一定的误差，尤其是前方车辆加速度无法精确量测.前方车辆的运动状态变化会对后方车辆控制系统稳定性和安全性造成较大影响.因此有些研究对前车的加速度进行了简化处理，直接假设领航车辆在预测时域内以匀速或匀加速度行驶，如文献［19-22］.此外还有些研究利用预测方程进行计算，常见的方法有非线性自回归（Nonlinear Auto Regressive，NAR）模型［16］和马尔可夫链蒙特卡洛（Markov Chain Monte Carlo，MCMC）仿 真［27］等.Morlock 等［28］利用交通历史数据，设计了基于高斯过程（Gaussian Process，GP）的未来交通流速度预测方法.上述预测方法的准确度均较低，易导致实际控制精度不理想.

随着V2V通信技术的成熟与应用，通过实时接收邻居车辆广播的运动状态信息和未来驾驶行为信息，参考轨迹的准确度有望得到显著提高.Anselma［29］利用V2V 通信获取前方车辆瞬时位置、速度和加速度信息，以能耗和行驶平顺性作为最优控制问题代价函数.但Anselma［29］采用了动态规划求解整个循环工况全局最优解，无法作为实时控制算法，且只对位置跟踪误差做了有界约束，无法保证误差的严格收敛.Spano等［30］基于前车的通信信息，采用等效能耗最小化策略（Equivalent Consumption Minimization Strategy，ECMS），设计了瞬时代价函数，所提出方法可用于实时控制，然而其同样未能保证跟踪误差的收敛性.

综上所述，基于V2V通信技术，在考虑能耗优化的同时，能够保证轨迹跟踪误差严格收敛至零点的ACC 算法目前还较少.因此，针对上述问题，本文研究智能网联车辆节能自适应巡航控制方法，主要贡献如下：

1）以轨迹跟踪为目标，设计了时变增益线性反馈控制律，并将反馈增益作为优化变量，构建一个经济最优控制问题以求解能耗代价最低的控制参数，基于模型预测控制方法设计了节能自适应巡航控制器，能够同时保证跟踪误差收敛性与燃油经济性.

2）通过构造共同Lyapunov 函数，分析了误差系统的渐近稳定性，给出了保证跟踪误差渐近收敛的控制参数选取条件.

本文按以下结构组织：在第1 节对车辆纵向动力学以及车辆能源消耗率进行建模，并给出自适应巡航控制轨迹跟踪目标；第2 节进行控制器设计和系统稳定性分析，并给出保证跟踪误差渐近收敛的控制参数选取条件；第3 节在MATLAB 中搭建系统模型进行仿真验证；第4节对本文进行总结.

1 系统建模

在本节中，首先建立智能网联车辆的纵向动力学模型和智能网联车辆的能源消耗率模型.然后，确定智能网联车辆自适应巡航控制的轨迹跟踪目标.

1.1 车辆纵向动力学建模

为简化问题分析，本文将车辆的行驶场景限定在平直路面上，因此只需对车辆纵向运动进行控制.考虑如图1 所示的车辆非线性纵向动力学模型，其描述如下：

式中：下标i为车辆索引；pi(t)和vi(t)分别表示车辆i在t时刻的位置与速度；Ti(t)和Tdes，i(t)分别表示实际与期望的驱动或制动力矩；mi为车辆的质量；rw，i为车轮半径；为集总空气阻力系数，其中CD为名义空气阻力系数，ρa表示空气密度，Av，i表示迎风面积，ζi(t)为阻力修正系数，如式（2）所示，其中表示车辆i与其前方车辆的距离，ξ1和ξ2为估计系数，其反映了由于车辆间距变化引起的空气阻力系数的变化，通过参数辨识获取［33］；ηT，i和fr，i分别为传动系统效率与滚动阻力系数；g为重力常数；τ表示动力系统时滞.为简化书写，时间标记(t)在下文中被部分省略.

为方便控制系统的分析，这里引入反馈线性化技术，其已经在诸多相关研究中被采用［34-35］.反馈线性化的表达式为：

其中，ui将被设置为线性化后的系统控制输入.实际控制时，系统确定ui后将根据式（3）计算期望力矩Tdes，i并据此控制执行机构动作.将线性系统状态向量记为xi=[pi，vi，ai]T，其中为车辆加速度.结合式（1）与式（3），可将车辆节点动力学转化为如下紧凑形式：

1.2 车辆能源消耗率模型

本文采用弗吉尼亚理工大学研究人员提出的基于功率的综合燃油消耗率模型（Virginia Tech Comprehensive Power-Based Fuel Consumption Model，VT-CPFCM）对车辆的能源消耗建模.瞬时燃油消耗率FC，i，g/s.采用二次多项式形式描述［36］：

其中，θ(·)，i为常数系数，Pd，i为车辆驱动系统的输出功率，kW.其根据车辆速度和加速度进行计算：

1.3 自适应巡航控制轨迹跟踪目标

本文考虑智能网联车辆可以依靠V2V通信交换车辆状态xi信息.

下文中使用下标“f”作为ACC 车辆的索引，即需要部署自动控制算法的车辆，下标“0”表示领航车辆.本文将ACC 轨迹跟踪目标设置为与前方领航车辆保持期望间距，并维持速度、加速度与领航车辆一致，数学描述如下：

其中，df(t)为期望车辆间距.

恒定时距策略（Constant Time Headway，CTH）有利于稳定性的设计，因此本文采用该策略定义车辆间距目标.将自适应巡航控制期望车辆间距设置如下［37-38］：

其中，h为车头时距常数，d0为静止间距，即速度为0时自身车辆与领航车辆的期望间距.

定义一个向量Df(t)=[df(t)，0，0]T，则自适应巡航车辆相对于领航车辆的跟踪误差向量可描述为：

2 控制器设计与系统稳定性分析

在本节中，首先针对式（9）设计了一个时变增益线性反馈控制律.其次，将反馈增益作为优化变量，构建一个经济最优控制问题以求解能耗代价最低的控制参数.再次，基于模型预测控制方法设计节能自适应巡航控制器.最后，构造共同Lyapunov 函数，并分析误差系统渐近稳定性，给出保证跟踪误差渐近收敛的控制参数选取条件.

2.1 切换增益线性反馈控制律

自适应巡航车辆基于如下线性比例反馈控制律计算控制输入：

其中，Kf(t)=[kp，f(t)，kv，f(t)，ka，f(t)]为时变的切换反馈增益，kp，f(t)、kv，f(t)和ka，f(t)分别为在t时刻的位置、速度和加速度反馈增益，其取值将由2.2节中的经济优化问题的解确定.

根据零阶保持假设（Zero-Order Hold Assumption）将连续时间动力学模型精确离散化，即在某一采样时刻，将连续系统控制输入uf(t)设置为与对应的离散系统控制输入uf(k)相同，并在下一采样时刻前保持不变［39］.结合式（10）与式（4），可得到离散车辆动力学模型，使用如下紧凑形式描述：

2.2 经济最优控制问题设计

本小节设计一个基于模型预测的经济最优控制问题，以优化式（10）中的反馈增益Kf(t).

使用Np表示模型预测控制的预测时域.在建立优化问题前，首先给出几个状态轨迹相关的定义：在t时刻，分别使用代表t+k时刻的自车预测状态轨迹和领航车辆假设状态轨迹，其中领航车辆假设状态轨迹在每个采样时刻通过V2V 通信接收.不同于基于前车速度预测的方法，自适应巡航车辆直接从前车接收其未来一段时间的假设状态轨迹，提高了参考轨迹准确性，有利于改善实际控制效果.本文中，自身预测状态轨迹基于动力学模型推算，用于参数化优化问题；领航车辆假设轨迹将被发送至自适应巡航车辆，其代表了领航车辆的运动趋势，取值由其自身预测状态轨迹确定.t时刻的预测反馈增益和最优反馈增益分别使用表示，其中最优反馈增益为经济最优控制问题的解.在整个预测时域内，采用同一个预测反馈增益

自适应巡航车辆的基于模型预测的经济最优控制问题描述为：

经济最优控制问题Pf(t)：

其中，lf为阶段代价函数，其代表了自身车辆在每个采样时刻单位位移的燃油消耗量：

在问题Pf(t)中为最小化车辆燃油消耗量，代价函数设置为整个预测时域内基于预测状态计算的各采样时刻每单位位移（m）燃油消耗量的累加.式（13）要求初始预测状态与当前时刻真实状态xf(t)相同；式（14）为车辆动力学约束；式（15）为反馈增益约束，考虑到系统稳定性，其将在2.4 节被详细设计与分析；考虑到驱动系统性能限制与乘坐舒适性，式（16）约束了控制输入的上界与下界.

2.3 节能自适应巡航控制算法设计

本小节基于上一小节设计的基于模型预测的经济最优控制问题和滚动优化策略设计节能自适应巡航控制算法.

节能自适应巡航控制算法流程如下：

算法1：（1）在t=0 时刻，初始化最优反馈增益和最优控制输入用于车辆实际控制.

（2）在任意t＞0的采样时刻：

（2.2）求解最优控制问题Pf(t)，获得最优反馈增益

重复步骤（2）至控制结束.

算法1的流程图如图2所示.

2.4 闭环误差系统的渐近稳定性分析

本小节基于上小节提出的反馈控制律，对式（9）的渐近稳定性进行分析.结合式（10），式（9）求导可得：

若u0可被自适应巡航车辆获取，则领航车辆的控制输入u0可被视为误差系统的参考输入，否则u0将被视为外部扰动.无论u0是否可知，针对式（18）的问题始终为控制综合问题.为降低理论难度，本文将控制综合问题简化为系统稳定性分析问题，为此需要对领航车辆行驶状态做出如下假设：

假设1：领航车辆的控制输入和加速度均为零，即u0(t)=0，a0(t)=0，∀t≥0.

采取以上假设，式（18）转化为：

其中，Af(t)=A-BKf(t)+H.可以发现式（19）为线性时变自治系统，且该系统的一个平衡状态为本节将采用Lyapunov方法判断此平衡点的稳定性.

记λ(M)为矩阵M的特征值，用A＜0 表示矩阵A的所有特征值均具有负实部.

在给出渐近稳定性结论前，首先给出如下引理：

引理1［40］：式（20）存在对称正定解P的充分必要条件为矩阵A∈Rn×n所有的特征值均具有负实部.

引理2（Comparison lemma）［41-42］：式（21）的解满足式（22）中的条件.

引理3：对于切换系统式（23），若存在正常数δ使得对于所有的切换信号σ，式（23）在初值条件|x(0)|＜δ下的解满足不等式（24），则称式（23）一致指数稳定：

其中，c＞0，λ＞0，e为自然常数.

利用上述引理，下面给出式（19）的渐近稳定性定理及证明.

定理1：采用算法1，若P是线性矩阵不等式组（Linear Matrix Inequalities，LMIs）式（25）和式（26）的对称正定解，Kf设置为式（27）形式，则式（19）是全局一致指数稳定的.

其中，r、α和β为正实数，且α＞β＞0.φf为反馈增益系数.

证明：首先设计一个式（19）的共同Lyapunov 函数.已知H为上三角矩阵，且其对角元素均为0，由三角矩阵特征值的性质可以得到：

根据引理1，式（29）总存在对称矩阵解P＞0：

即式（26）总有解.

取一个二次型函数如式（30）：

不难验证Vf(t) ＞0.

采用符号He(A)表示矩阵A和其转置矩阵的和，即He(A)=A+AT.结合定理1中的条件，对式（30）进行求导：

即Vf(t)随时间增加呈指数趋势衰减.

接下来，证明随着时间T趋向于无穷，误差向量收敛至零点.

记‖x‖p为向量x的p范数（p-norm）.通过提取二次型矩阵特征值，可以得到：

结合式（32）、式（33）和式（34），可得到如下不等式：

根据引理3 以及式（36）的结论，式（19）是全局一致指数稳定的.

上述证明构造了式（30）所示的共同Lyapunov 函数，且反馈增益Kf(t)的切换不会影响其取值大小和衰减速度，因此实现了任意切换条件下式（19）的渐近稳定性.

3 数值仿真验证

设置领航车辆的初始状态为p0(0)=0 m；v0(0)=15 m/s；自适应巡航车辆的初始状态为pf(0)=-df(0) m；vf(0)=15 m/s；af(0)=0 m/s2.车辆模型参数和控制参数如表1 所示，本文中部分模型参数参考文献［43］中的2010 款Nissan Micra 车型参数.

表1 节能自适应巡航控制模型及控制参数Tab.1 Energy-saving adaptive cruise control model and control parameters

本节采用的式（25）和式（26）的解为：

3.1 跟踪性能验证

首先，基于定理1，验证自适应巡航控制跟踪目标式（7）的实现.为更贴近真实行驶工况，考虑领航车辆的速度存在变化，即假设1非恒成立.

在此场景中，领航车辆的加速度以正弦规律变化，如下式所示：

其中，加速度变化的幅度为Aa=1 m/s2；加速度变化的频率为ωa=2π/15 rad/s.

自适应巡航车辆的状态与跟踪误差仿真结果如图3 所示，其中Δpf=p0-pf-l0为自适应巡航车辆与领航车辆的相对距离.时变反馈增益变化曲线如图4 所示.可以观察到，在领航车辆速度变化期间，即假设1 不成立时，各个状态跟踪误差虽无法严格收敛，但仍保持在零点附近，此时算法的跟踪性能是可以接受的.在领航车辆结束速度变化后，各个状态跟踪误差逐渐收敛至零点，即达到式（7）条件，此结果验证了算法1 的渐近稳定性.且时变反馈增益的变化趋势与领航车辆速度的变化基本一致，并最终收敛在约束下界，也说明了选取反馈增益作为优化变量求解经济最优控制问题的合理性.

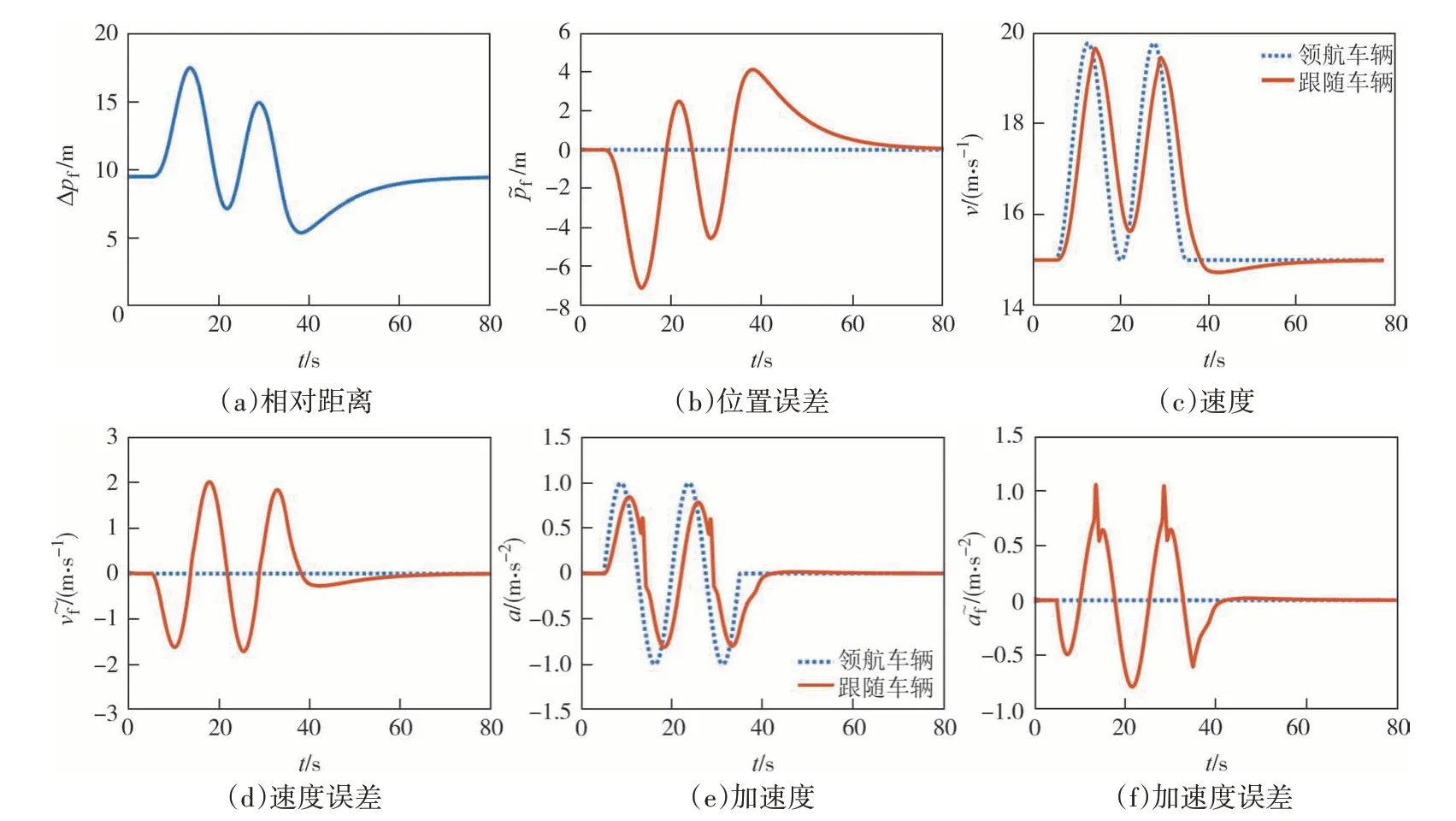
图3 节能自适应巡航控制车辆状态与状态跟踪误差曲线Fig.3 Energy-efficient adaptive cruise control vehicle status and status tracking error curves

图4 时变反馈增益变化曲线Fig.4 Time-varying feedback gain curve

系统模型式（4）是经过线性化处理之后的模型，可能会导致实际控制性能和仿真结果在跟踪精度方面出现偏差.图5 为考虑不精确的线性化引起的模型不匹配和外部扰动的自适应巡航车辆的状态与跟踪误差仿真结果.仿真中，动力系统时滞τ=0.4 +0.2 ×w，其中w∈[0，1]为均匀分布的随机变量.另外车辆受到均匀随机输入干扰ud∈［-0.1，0.1］，m/s2.与图4 的仿真结果进行比较，跟踪性能基本一致，表明了所提出的方法在线性化处理的情况下的有效性.

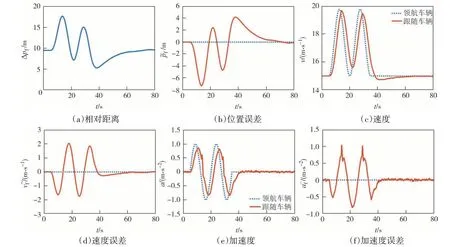
图5 模型不匹配和输入扰动情况下的仿真结果Fig.5 Simulations results with model mismatches and input disturbances

3.2 节能性能验证

本小节将节能自适应巡航控制算法1，经济模型预测控制算法（Economic Model Predictive Control，EMPC）与两个基准算法的控制性能作对比，验证所提出算法在提高燃油经济性方面的效果.基准算法1为静态反馈增益控制算法（Static Feedback Gain Control，SFGC），即φf(t)被设置为固定值1.25；基准算法2参考文献［44］，设置为以跟踪为目标的模型预测控制算法（Tracking-oriented Model Predictive Control，TMPC），其最优控制问题阶段代价函数设置如下：

首先考虑与3.1 节相同的领航车辆加速度做正弦波动的工况.采用基准算法1 和基准算法2 时，自适应巡航车辆的位置跟踪误差如图6 所示.行驶过程中瞬时燃油消耗率FC，f(t)曲线对比如图7所示.总体来看，在速度变化期间，本文所提出的切换反馈增益节能控制算法具有更低的燃油消耗率.不同算法下自适应巡航车辆整个行驶过程的燃油消耗总量如表2 所示.与SFGC 算法和TMPC 算法相比，EMPC 算法的总油耗量分别降低了3.51%和4.01%.上述结果验证了本文的节能自适应巡航控制算法在降低燃油消耗量方面的有效性.不同算法加速度正弦波动工况下的位置误差如表3所示.比较表3位置跟踪误差与表2 总油耗量结果发现，本文算法虽具有更好的燃油经济性，但跟踪精度与基准算法相比有所下降，这在一定程度上体现了跟踪精度与节能性能之间的冲突性.

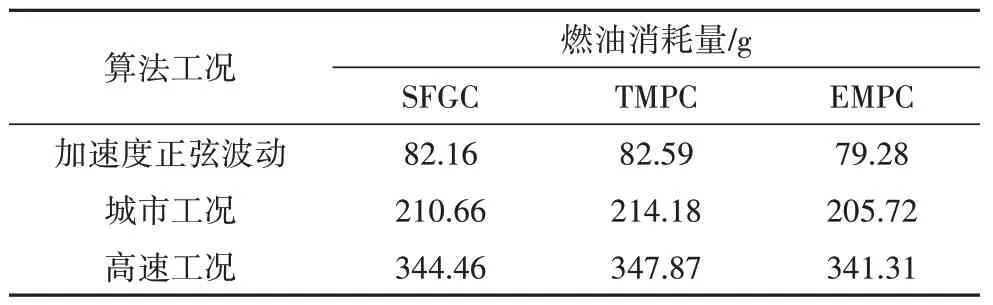
表2 不同算法与工况下自适应巡航控制油耗量Tab.2 Adaptive cruise control fuel consumption under different algorithms and operating conditions

表3 不同算法加速度正弦波动工况下位置误差Tab.3 Position error under sinusoidal fluctuation conditions of acceleration of different algorithms

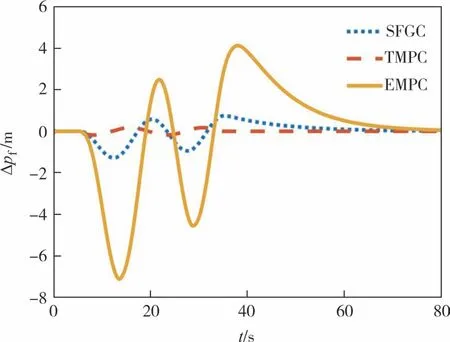
图6 不同算法下自适应巡航控制位置误差曲线Fig.6 Adaptive cruise control position error curve under different algorithms

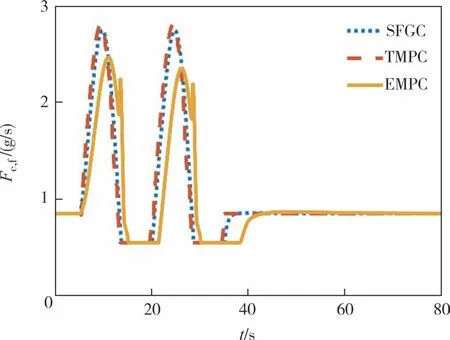
图7 不同算法下瞬时燃油消耗率对比Fig.7 Comparison of instantaneous fuel consumption rates under different algorithms

为验证本文所提出方法在更真实的循环工况中的性能，考虑领航车辆在城市工况和高速工况行驶，其速度曲线如图8所示.

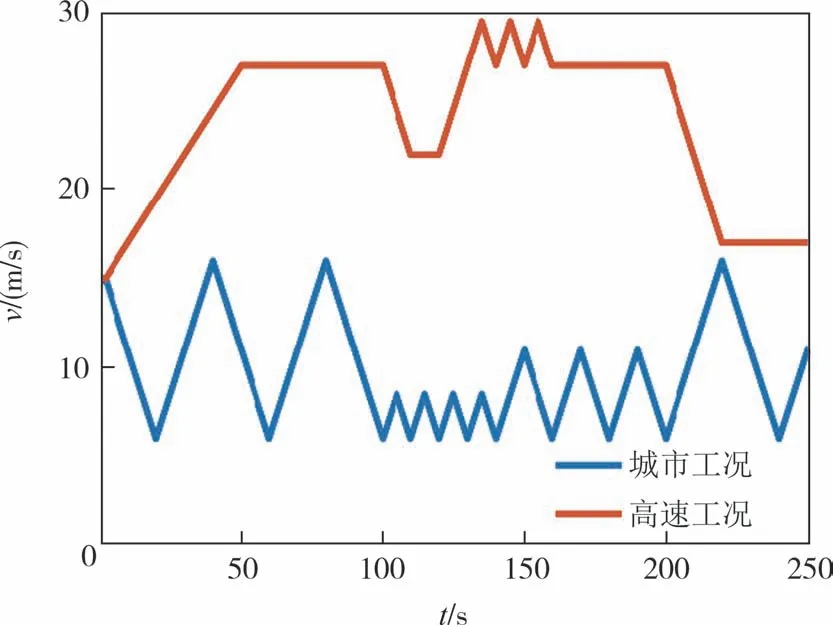
图8 城市和高速行驶工况的速度曲线［32］Fig.8 Speed curves for urban and high-speed driving conditions［32］

在不同控制算法下，跟随车辆的总燃油消耗量结果列于表2中.与SFGC算法和TMPC 算法相比：在城市工况下，EMPC 算法的能耗分别降低了2.35%和3.95%；在高速工况下，EMPC 算法的能耗分别降低了0.91%和1.86%.上述结果验证了本文所提出方法在真实工况下的有效性.另外，还可注意到在城市工况下，油耗量降低的比例更大，此现象说明车速波动较频繁时，EMPC 算法可能具有更佳的经济性提升效果.

所提出的EMPC 算法在领航车辆加速度正弦波动工况下的计算时间如图9 所示，求解平均计算时间为4.621 ms，明显小于采样时间，说明所提出的算法满足实时性要求.

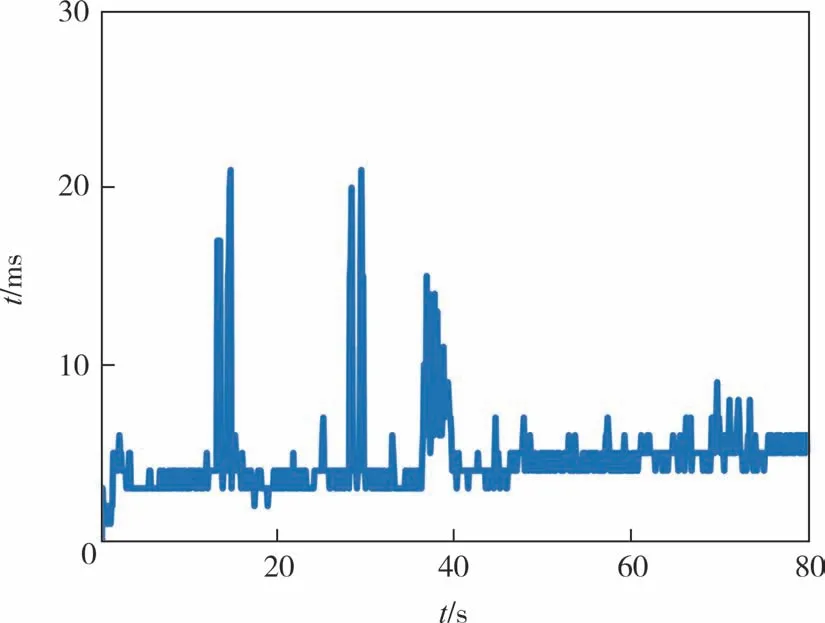
图9 EMPC算法计算时间Fig.9 The calculation time of the EMPC algorithm

4 结论

本文针对车辆自适应巡航控制设计了以降低燃油消耗量为目标的经济模型预测控制器；提出的方法直接将智能网联车辆的燃油消耗率作为代价函数，将时变反馈增益作为优化变量，能够直接显式地优化燃油经济性；并且基于Lyapunov 方法和切换系统理论给出了闭环误差系统的渐近稳定性条件.数值仿真结果表明，本文设计的车辆节能自适应巡航控制器能够在有误差严格收敛需求的场景中，保证可接受的跟踪精度的同时，提高车辆的燃油经济性.本文将车辆的行驶场景限定在平直路面上，其曲率较小，横向运动对燃油经济性能影响较小，因此忽略了横向运动的影响.如果将所提出的算法扩展到非平直路面，需要进一步考虑滚动阻力、纵向滑移率和偏航力矩等因素的影响［45］.