基于时空图注意力的短期电力负荷预测方法

李文英 ，杨高才 ，文明 ，罗姝晨 ，于宗超 ，姜羽 ，王鼎湘

（1.国网湖南省电力有限公司经济技术研究院，湖南 长沙 410000；2.湖南大学 电气与信息工程学院，湖南 长沙 410082）

电力系统需要满足负荷需求，不间断地稳定供应电力.通过分析电力负荷的历史行为、趋势及影响因素，预测未来需求，称为电力负荷预测.近年来，电力系统整合了多种电力资源（如可再生能源），其中具有较强波动性的风能和太阳能将负荷预测现象推向了一个更具挑战性的阶段.从电力系统的角度来看，可靠的预测结果可以有效减少风能和太阳能发电不确定性的不利影响，帮助调度部门及时制定和调整调度计划，降低运行成本.负荷预测是实现电力供需平衡的前提，在电力规划中起着至关重要的作用.

电力负荷的预测方法按时间尺度可分为四种：超短期预测［1］、短期预测［2-4］、中期预测［5］和长期预测［6］.其中，短期负荷预测结果可为电力系统调度方案的制定提供依据.

现有的负荷预测方法可分为两类：经典的基于模型的方法和基于机器学习的方法.基于模型的负荷预测是一种非黑箱模型［7］.常用的方法有回归分析［8］、指数平滑［9］、加权最小二乘［10］等.负荷预测结果与其驱动因素之间的对应关系是明确的，但在预测前需要了解负荷特性并明确模型类型，要根据场景选择预测方法，保证预测的准确性.基于模型的预测方法在使用时具有极大的局限性，并且模型主要是捕获线性关系，在处理较为复杂的时序数据时达不到理想的预测精度.

除了经典的基于模型的方法外，由于机器学习方法能拟合时序数据各时间戳的非线性关系，基于机器学习的方法近年来也越来越受到关注.该种方法主要使用支持向量回归、基于核的方法和前馈神经网络等，通过特征工程构造对预测结果具有因果的特征集合，最终得到时序预测模型.然而，这些模型中的大多数仅实现了静态建模预测，在单独的时间尺度上考虑信息，而不能挖掘多变量时序数据间的动态依赖关系.

深度神经网络具有较强的非线性拟合能力，能够学习复杂的多变量时序数据表示.目前，学者们已开发出不同的深度神经网络来解决时间序列预测问题，例如使用循环神经网络及其变体，自编码器、时间卷积和Transformer等.

由于同一街区内的住宅可能受到相似因素的影响，各住宅的电力负荷具有一定的潜在空间依赖性.然而，现有的大多数基于机器学习的方法仅利用电力负荷和天气信息等历史时间值，未能探索这种依赖关系，不同单位之间的空间相关性［11］通常被忽略［12］.图神经网络（GNN）能够挖掘单元间的潜在依赖关系，目前在交通流预测和风速预测等任务中的应用已经证明了其优越性.与深度神经网络不同，GNN 擅长对类似图的数据结构进行建模，这使得它们非常适合捕获电网中不同住宅之间复杂的潜在空间依赖性.然而，基于GNN 的时空模型却很少用于电力负荷预测问题研究，主要由于其在使用过程中可能遇到下述问题：

1）GNN 需要图结构作为基础，而电力负荷数据并没有显示的图结构.目前一些研究使用k-近邻来创建正则的图结构.然而当使用不恰当的k构建图结构时，会产生过平滑或冗余的问题.使用较小的k构建出来的图结构，为了聚合和更新图结构上的全部节点信息，需要增加后续GNN 的层数，然而GNN 是一种低通滤波器［13］，当GNN 的层数过多时，会产生过平滑的问题.使用较大的k构建出来的图结构，会将不存在的关系引入图结构，为后续耦合关系的提取带来误差［14］.

2）变量之间的耦合关系随着时间的推移而变化，如何动态地捕捉变量之间的关系是一个值得考虑的问题.

3）用于捕捉时序特征的RNN（循环神经网络）/GRU（门控循环单元）/LSTM（长短时记忆网络）虽然擅长描述非线性关系，但没有考虑到因果时滞效应，对于时序数据的记忆有限，难以捕捉长期依赖关系.

针对上述问题，本文提出了一种基于小世界理论的多变量时间序列预测方法——小世界时空图注意力网络（Small-World Spatio-Temporal Graph Attention Network，SWST-GAT）.在电力负荷预测中自适应的建模与捕捉同一街区内的住宅用电量间的潜在空间依赖性，解决了现有多变量多步负荷预测技术中的问题.主要贡献具体如下：

1）提出一种基于小世界特性的k-近邻网络构建技术，解决了GNN 在多变量时序分析中图建模时存在的过平滑或冗余的问题.

2）提出了一个基于节点重要性引导的注意力机制，与图注意层相结合，动态地捕捉变量之间的耦合关系.

3）使用门控扩张因果卷积层提取时间序列数据的因果时滞特征，捕捉长期依赖关系，并提出基于动态系统的复杂性和耗散性质的超参数时间跨度和扩张率估计，帮助门控扩张因果卷积层的超参数选取.

1 小世界时空图卷积网络模型

本文提出的SWST-GAT 模型的任务是对多变量时序X∈ℝN×n×d进行图结构构建后，将图结构与多变量时序数据X∈ℝN×n×d输入到ST-GCM 模块中，使用空间卷积层提取各个变量间的耦合关系，使用时间卷积层提取每一个变量在时间维度的因果时滞关系，时间与空间卷积层交替作用，以同时提取多变量时序数据的时空特征，对变量时序数据X∈ℝN×n×d进行拟合，预测下一时刻的目标变量yi，t+TS+1或下一段时间的目标变量Y=［yi，t+TS+1，yi，t+TS+2，…，yi，t+TS+pr］，使用最小正则化L2损失来训练网络，以构建从X到Y映射（f·）.

1.1 模型介绍

本文提出的多变量时序多步预测模型SWSTGAT的总体框架如图1所示，具体概括如下.

图1 SWST-GAT的网络架构Fig.1 Network structure of SWST-GAT

1）图结构构建模块：提出一种基于小世界特性的k-近邻网络构建技术，构建多变量时间序列的静态图结构G=（V，E），其中V为节点集合，每一个节点代表一个变量，E是边集，每条边表示边两端的节点间存在耦合关系.

2）ST-GCM：ST-GCM 为“三明治”结构，由NA、GCN 和GDCCN 组成.因此，NA 将度中心性引导的注意力机制（Degree Centrality Guided Attention，DCGA）和压缩激励模块（Squeeze and Excitation Networks，SENet）相结合来自动学习各个节点和连边的相对重要性，增加重要的节点和连边的权重，抑制无用的节点和连边的权重，同时使用GDCCN 捕捉变量的时间维度的因果时滞特征.

3）为了确定GDCCN 层的两个关键超参数的选择，提出了基于动态系统的复杂性和耗散性质的TS估计和dr估计算法.

1.2 图结构构造模块

由于k的选择关系到网络的拓扑结构是否能够反映多变量时间序列的分布，因此，邻近数k在网络构建过程中起着非常重要的作用［15］.目前讨论如何选择邻近数k的研究成果较少.当选择较小的k时，我们将得到一个极其稀疏的随机网络，此时图结构不连通，产生信息孤岛，多变量间的信息并不能共享.当k逐渐增大时，网络将开始向全连接网络演进，网络连接会逐渐变密，导致网络极度冗余.图结构的传播效率和稀疏性可通过复杂网络的网络平均一致性h和网络平均聚类系数ACC 进行描述，h用于衡量复杂网络的全局传输容量；ACC 用于量化复杂网络中节点之间的连接程度.其计算公式如下：

其中，h为全局效率（Global Efficiency，GE）的逆，GE与网络中节点之间的距离成反比.表示节点vi到节点vj之间的最短距离.

其中，ki（ki-1）/2 是ki相邻节点之间可能的边数，E（i）是节点vi的ki相邻节点之间的实际边数.

因此，本文拟通过h和ACC 对图结构传播效率和稀疏性的定量计算，寻找两者之间的平衡，从而确定邻近数k.基于小世界网络性质的自适应k-近邻选择算法的流程如图2所示.

图2 基于小世界网络性质的自适应k-近邻选择算法Fig.2 Adaptive k-nearest neighbor selection algorithm based on small-world network properties

根据小世界网络生成的过程，提出基于小世界网络的邻接矩阵生成算法，如算法1 所示.具体步骤如下：首先，根据多变量时序数据X计算任意两个变量间的相似性S=X·XT，并进行归一化，得到相似性矩阵S.随后，将邻近数k设为0，得到一个全断开的图结构；最后，逐渐增大邻近数k至N，在此过程中，图结构会逐渐变得稠密，此时ACC 逐渐变大，h逐渐变小，分别计算对应的h（A）和ACC（A），最终形成如图2 右侧所示的h（A）和ACC（A）曲线。选择h（A）和ACC（A）曲线的交（ratio，k）作为邻近数k，根据选择到的邻近数k，进行图结构A的构建，具体定义公式如下：

其中，Neighk（vi）为距离节点vi最近的k个节点的集合.最后针对每一个节点，随机选择两个未与其相连接的节点，以概率p进行连接.

1.3 时空图卷积模块

由于多变量时序数据具有强耦合和大时滞的特点，变量之间的时空关系是复杂且时变的，如图3 所示.因此我们提出一种新的ST-GCM 针对多变量时序数据的时空特性进行处理.

图3 多变量时序数据的时空特性Fig.3 The spatiotemporal characteristics of multivariate temporal data

1.3.1 时间卷积层

GDCCN 的架构如图4 所示，包含一个扩张因果卷积网 络（Dilated Causal Convolution Network，DCCN）［16］、一个门控线性单元（Gated linear units，GLU）［17］和一个 残差模 块［18］，GDCCN 层的计算公式为：

图4 GDCCN的架构Fig.4 Network structure of GDCNN

其中，X和XGDCNN为GDCCN 的输入和输出，WG、VG、cG和bG为GDCCN 层的可学习参数，*G和*D为门控卷积和扩展卷积核，σ为ReLU函数，⊗ 为哈达马积.

1）扩张因果卷积网络

不同于传统非线性动态过程系统建模包含较多的历史数据，本文使用DCCN 解决了长期预测结果精度降低的问题.在使用CNN（卷积神经网络）或者RNN 进行长距离时间序列预测时，不可避免地需要增加CNN 的层数或RNN 的卷积核大小，此时网络参数和计算量将大大增加.DCCN 使用具有空洞的CNN，可以在不增加网络参数的情况下扩大卷积核的视野，如图5 所示.扩张卷积的核心思想是将原本紧密相连的卷积核参数按照设定的比值进行扩张.扩张卷积的计算公式为

图5 扩张因果卷积Fig.5 Dilated causal convolution network

其中，dr 为膨胀比，k为卷积核的大小，xt-dr·i为历史数据.

2）门控线性单元

GLU 是一种简化的门控机制，可以减少梯度分散问题，保持层的非线性，加速收敛，其结构如图6所示.

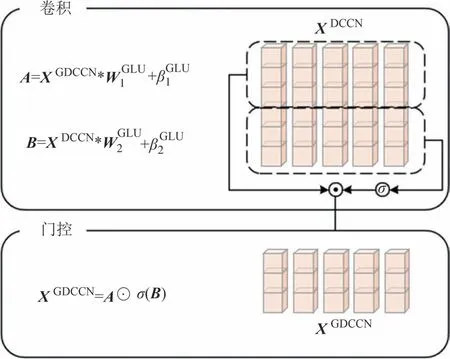
图6 GLU架构Fig.6 Structure of GLU

GLU利用CNN和并行处理时序数据的门控机制来实现RNN的功能.GLU在处理时序数据时，严格按照时序位置保存信息，以提高性能，并通过并行处理结构加快运算速度.GLU的公式如下：

其中，XDCCN和XGDCCN是GLU 的输入和输出矩阵，是可学习的参数，σ为ReLU函数，⊗ 为哈达马积.

1.3.2 空间卷积层

1）节点注意力层

NA 包含一个DCGA 和一个SENet［19］.NA 层的计算公式为：

其中，XNA为NA 层的输出数据，WSENet为SENet 模块的可学习参数，Fscale，Fex和Fsq为SENet 的缩放、激励和压缩操作，AttDC∈ℝN×N是根据节点嵌入计算出的度中心性引导的注意力：

其中，DC（·）为度中心性计算函数，矩阵E1和E2为随机初始化的节点嵌入，在模型训练期间可以学习，为可训练的模型参数.

作为软注意力机制的一种应用，SENet不同于传统的通过添加特征卷积层来细化特征提取任务的方法，而是根据特征响应显式，建模特征图通道之间的相互依赖性，自适应地重新校准通道.由于多变量时序数据是典型的时空数据，因此变量之间的耦合关系会随着时间而改变.因此，本文将使用SENet 自动学习不同通道特征的相对重要性，然后可以通过赋予不同的权重来增强或抑制相应的特征，从而提高网络模型的识别精度.SENet的结构如图7所示.

图7 SENet的架构Fig.7 Structure of SENet

SENet 分为挤压和激励两步操作.首先，SENet对输入节点变量执行挤压操作，将特征形状从N×1×TS压缩为N×1×1，得到该层输入节点变量的分布，其数学描述如下：

其中，x（1，t）∈ℝN×1是t时刻N个节点的数据，TS 为网络输入数据的时间长度.压缩操作通常采用全局最大池化或全局平均池化两种算法，最后将全局空间信息压缩成一个通道维度描述符xq，本文选择全局平均池化.

激励操作定义如下：

其 中，W1SENet∈ℝ（TS/β×TS）和W2SENet∈ℝTS×（TS/β），σ是ReLU 函数，β是维度变换率.

最后将得到的缩放矩阵sc的元素与图数据的通道一一相乘，SENet的输出定义为：

其中，sci是第i个节点向量xi的缩放系数.SENet 的运行充分利用了注意力机制，使模型在训练过程中会关注更重要的节点，从而提高模型的整体性能.

2）图卷积层

使用Chebyshev 多项式改进的GCN 提取空间特征［20］，其结构如图8 所 示.GCN 的卷积核为gθ=是i阶多项式，Λ为邻接矩阵A的特征值.Chebyshev 多项式通过递归计算得到，其计算公式如下：

图8 GCN的架构Fig.8 Structure of GCN

图卷积核的卷积操作的计算式如下：

其中，XNA和XGCN是GCN 层的输入和输出矩阵，WGCN是可学习的参数，*G为Chebyshev 多项式构造出的卷积核.

1.4 超参数估计

1.4.1 时间跨度估计

时间跨度TS 是时间卷积层GDCCN 的卷积核的大小.在前期研究准备过程中，我们发现现有文献中对TS 的选择是基于经验的.例如，交通流量预测中一般选择24（一天24 小时）×7（一周7 天），并且这种经验选择仍然用于文献［21］中的所有多变量时序数据集.但是对于不同领域内的数据集，例如工业或金融数据集，使用这个经验值是不合适的.为了解决这个问题，提出了一个时间跨度估计算子以估计GDCCN的卷积核的大小.

考虑到更有效地利用时间序列中包含的信息，使用信息论中的经典指标：CD 和LS，估计能够等效包含原始动态信息的时间维数的最小值［22］，将其作为时间跨度TS.CD 反映了动态系统中不规则变化的程度.系统变化越复杂，CD 越大，表示系统演化所需的数据维数也越高.此外，任何耗散系统的LS 中至少有一个维度应小于0，并且所有维度之和应小于0.因此，当选择的TS 不能覆盖时间序列数据的时间动态时，LS 各项之和大于零.基于此，本文提出了一种基于动态系统分析的时间跨度估计算法.伪代码如算法2所示.

1.4.2 扩张率估计

时间序列中的每一组收集到的多变量时序数据都是各种影响因素的综合结果，这些影响因素大致可以分为三种：趋势性、周期性和随机性.每一时刻多变量的实际变化通常是由若干影响因素的叠加或组合引起的.因为工业领域的变量具有不同的物理意义，所以每个变量的趋势和周期变化很可能是不同的.本节将变量的趋势和周期变化定义为时间节律.

基于此，本文采用基于动态系统分析的方法对节律时钟进行估计，以指导扩张率的选择.选择互信息（Mutual information，MI）来估计每个变量xi的时间节律T（i，i）.T（i，i）的计算公式如下：

T（i，i）是I（xi）的第一个局部最小值，表示系统获取信息的时间尺度.同时，我们计算T（i，j）得到变量xi和变量xj之间的延迟时间，并进行数据对齐.扩张卷积数据对齐流程图如图9 所示，右上角的子图是变量之间的对齐过程.xi是要预测的变量.xj的t+T（xi，xj）时刻和xk的t+T（xi，xk）时刻与xi的t时刻对齐.右下角的子图显示了不同扩张率的扩张卷积对不同变量的处理.

1.5 模型训练与测试

均方误差损失函数用于模型训练优化，损失函数的定义式为：

其中，n是时间序列中训练数据的总数，Y是真实值，是预测值.

根据上述SWST-GAT框架，利用Adam优化算法在反向传播中对每个权重参数求网络误差的梯度，通过参数更新过程得到新的权重.迭代计算模型权重，直到达到预定的小损失，并获得最佳预测值。选择Adam 作为优化算法的原因是它可以为不同的参数设计独立的自适应学习率，计算效率较高.训练算法具体细节在算法3中给出.

2 电力负荷预测实验分析

本节将在电力负荷数据EL上验证所提出的网络SWST-GAT 的预测性能，EL 数据集是新加坡某电站2012～2014 年间321 个客户的用电量（kWh），采样频率为15 min.数据集存放有26 304个变量数为321的样本，采样率为1 h.数据对应Lyapunov谱如图10（a）所示，根据基于小世界网络性质的自适应k-近邻选择算法，计算得到的h和ACC（G）曲线如图10（b）所示，因此，选定数据集时间跨度TS=4、近邻数k=83.本节所有实验均在Windows 系统上编译和测试（CPU：Intel（R）Core（TM）i9-10900K CPU @ 3.70 GHz，GPU：NVIDIA GeForce RTX 3 090）.

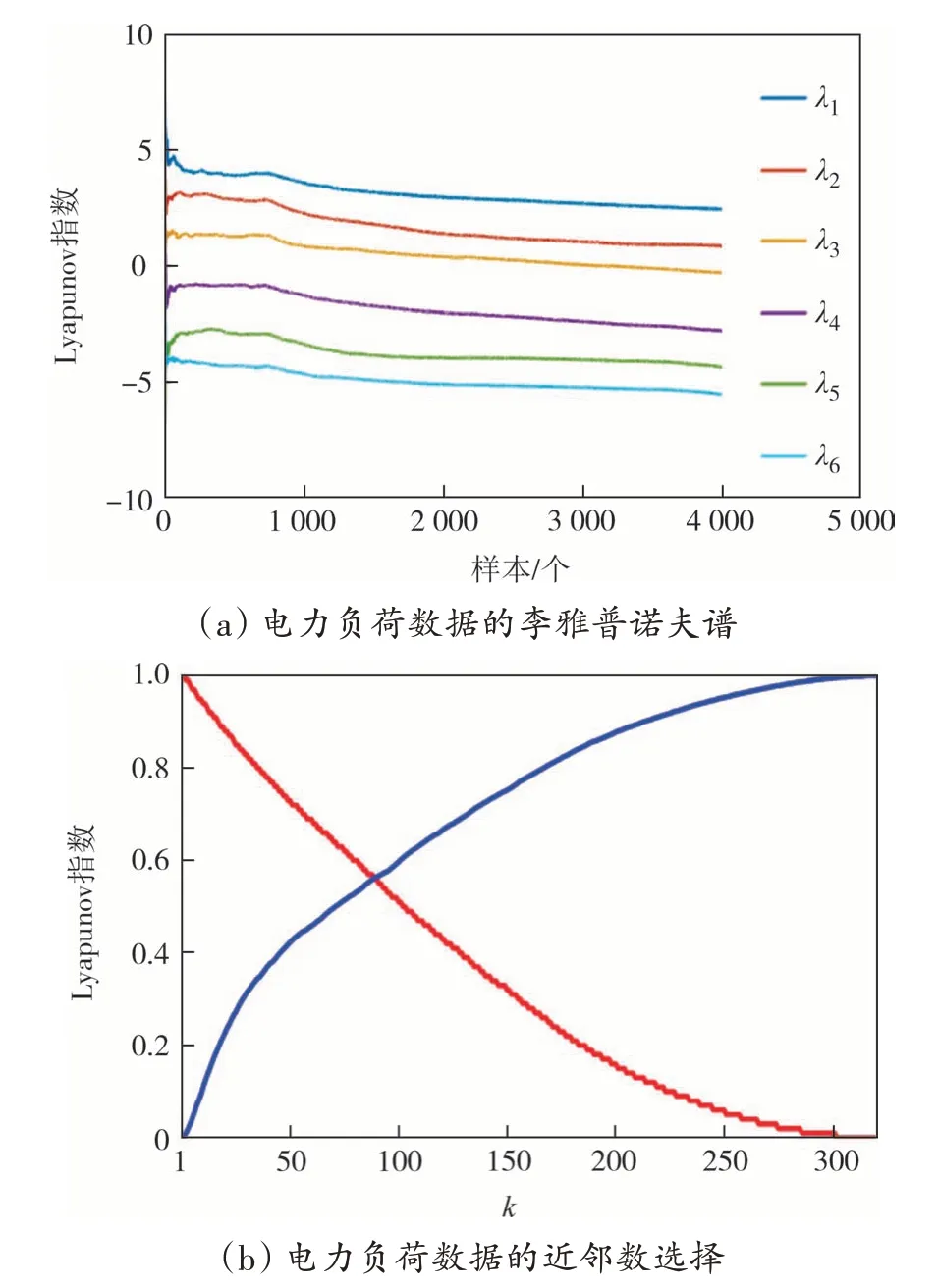
图10 新加坡某电站2012～2014年间电力负荷情况Fig.10 The power load of a power station in Singapore from 2012 to 2014

针对模型的预测精度，本文使用五个评价指标对预测性能进行评价，包括平均绝对误差（Mean Absolute Error，MAE）、均方根误差（Root Mean Square Error，RMSE）、平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）和相关系数（Correlation Coefficient，CC）.MAE，RMSE，MAPE的值越小，CC的值越大，所评价模型的预测精度越高.

2.1 实验结果

为了证明SWST-GAT 的有效性，将SWST-GAT与五个多变量时序预测模型进行比较，模型的简要描述在表1 中列出.五个对比模型分别为TPALSTM［23］、LSTNet［24］、DCGNet［25］、Graph WaveNet［26］和MTGNN［21］.TPA-LSTM 使用一组滤波器来提取时不变的时间模式.在此基础上，提出了一种新的注意机制来选择相关的时间序列，进行预测；LSTNet 使用CNN 来提取变量之间的短期局部依赖模式，并使用RNN发现时间序列趋的长期模式.同时，利用传统的自回归模型来解决神经网络模型的尺度不敏感问题；DCGNet使用深度CNN提取多变量的局部耦合特征和门控循环单元网络提取时间维度的非线性动态特征；Graph WaveNet 通过建立一个新的自适应依赖矩阵，对节点嵌入进行学习，捕获数据中隐藏的空间依赖，同时使用一维的CNN进行长序列的特征提取；MTGNN 提出一个单向图结构生成算法，并结合DCCN和GCN对多变量数据进行预测.

表1 对比模型的简要描述Tab.1 Brief description of the comparative model

所有比较的方法都使用滑动窗口输入，表2 总结了六种模型的评估结果，最优结果用红色字体加粗显示，次优结果用加粗显示.六种预测方法的真实值与预测值对比如图11 所示，对应的预测误差曲线如图12 所示.从评估结果可以看出本节提出的SWST-GAT 模型预测精度最好，RMSE 和MAE 最小，CC 最大，表明真实值和预测值之间变化趋势基本一致.

表2 模型评估结果Tab.2 Model evaluation results

图11 不同模型的预测值与真实值Fig.11 Predicted and true values of different models

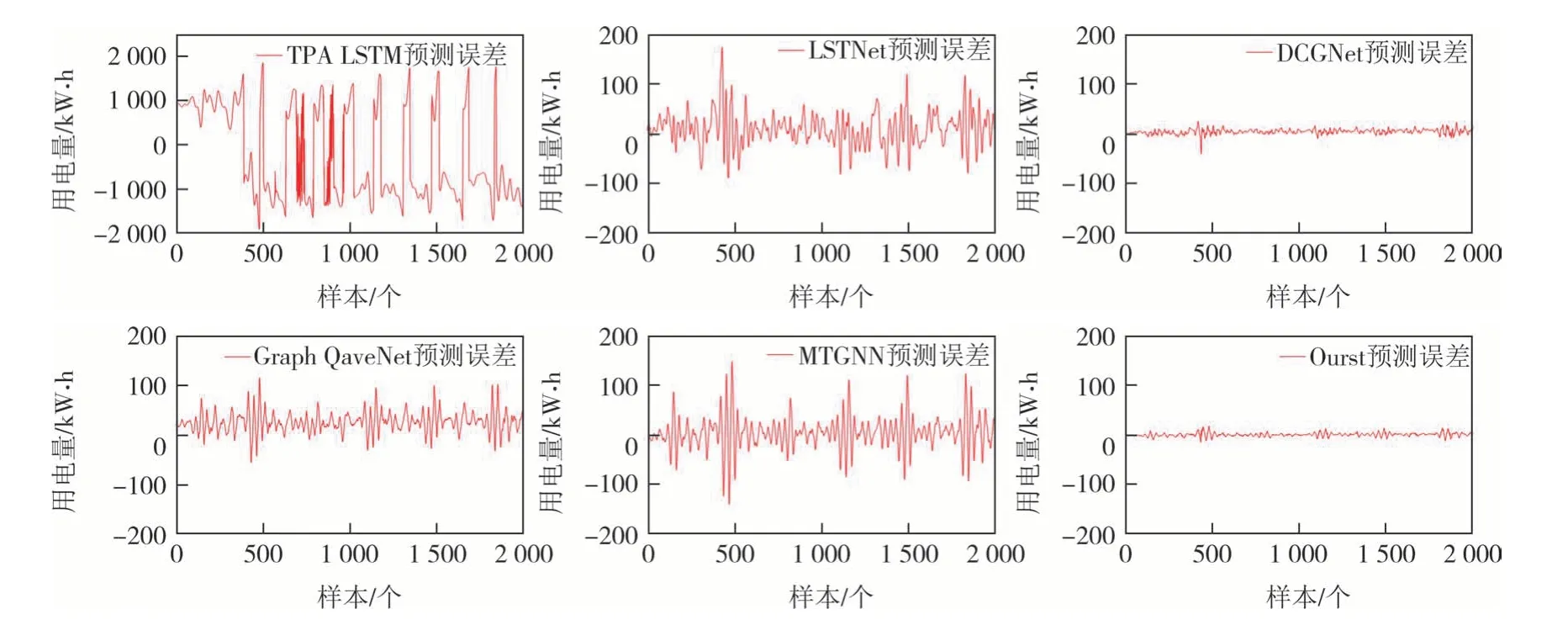
图12 不同模型的预测值与真实值的误差Fig.12 Error between predicted and true values of different models

基 于LSTM 的TPA-LSTM 和LSTNet 模型的MAE、RMSE 和MAPE 明显高于其他模型，预测精度最低，表明这类模型不能轻易地适应实际值的局部趋势.与上述两种模型相比，结合动态RNN 的DCGNet模型的预测精度有了显著提高，在部分数据集上取得了次优结果，如表2 所示，在混合模型DCGNet模型的短程预测中，预测曲线符合实际趋势.基于GCN 的Graph WaveNet 和MTGNN 与表2 中的静态和动态循环网络相比，进一步验证了GNN 在考虑变量间耦合关系的后处理多变量时间序列方面的有效性，尤其在长程预测方面.与所提出模型的预测性能相比，这些网络的预测性可以进一步提高.

此外，为了进一步评价不同预测模型的性能，引入了误差概率分布曲线.图13 为六种不同预测模型下预测残差的概率分布.与其他模型相比，本文模型得到的预测值的误差分布更接近于0，变化更小，进一步说明了本文方法的可靠性.

图13 不同模型的预测值与真实值的误差Fig.13 Error between predicted and true values of different models

2.2 模块有效性分析

为了证明邻接矩阵构建的近邻数k选择和GDCCN 的时间跨度选扩张率的选择的有效性，进行了消融实验.首先定义不同的模型如下.

1）our-0.1：选择连接最近的0.1N个邻居.

2）our-0.8：选择连接最近的0.8N个邻居.

3）our-nTS：不使用时间跨度估计模块.

4）our-nDCGA：不使用基于DCGA.

5）our-nSENet：不使用SENet模块.

6）our-ndr：不使用扩张率估计模块.

对于上述模型，评价指标测得的测试结果如表3所示.

表3 消融实验结果Tab.3 Results of ablation experiments

从这些实验结果得出的几个结论总结如下.

1）本文提出的基于小世界网络的邻接矩阵生成算法确实可以在保证预测精度的同时减少计算量.通过与our-0.1和our-0.8的结果相对比，可以看出当近邻数k足够大时，即使增大k，也不会提高整体算法的性能，有时反而会造成性能的衰退.造成这种情况的原因可能是大量无关的边相连后导致的图结构的扭曲，与真实的多变量间的耦合情况相去甚远，造成后续利用耦合关系进行预测的GCN 的性能的下降.若选择的近邻数k较小，则无法通过图结构详细的表示出多变量间的耦合关系，导致GCN 提取的网络耦合关系不足以完成高精度的预测.

2）SENet 和NA 确实可以增加对预测影响较大的变量的权重，抑制对预测影响较小的变量的权重，提高预测精度；

3）GDCCN 的超参数选择十分重要，当沿用经验设定值时，模型的效果大打折扣.造成这种情况的原因可能是时间序列中的每一组收集到的多变量时序数据都是各种影响因素的综合结果.每一时刻多变量的实际变化通常是由若干影响因素的叠加或组合引起的.因为来自不同系统的变量具有不同的物理意义，所以每个变量的趋势和周期变化很可能是不同的.

3 结论

本文针对电力负荷预测中多变量间的非线性耦合特性难建模问题，提出了一种基于小世界理论的模型SWST-GAT，用于多变量时间序列的动态长程预测.针对多变量时序数据没有清晰图结构的问题，设计了权衡网络全局效率和冗余度的图基本结构构建算法；针对多变量时序变量间存在时滞的问题，构建了一个全新的时间卷积层以捕捉较长历史数据内的非线性关联关系；针对网络超参数选取凭经验的问题，提出了一种基于复杂动态系统的超参数估计方法，避免经验值导致长程预测效果的减弱.得到结论如下：

1）相比于使用CNN 捕获多变量间关系的方法，多变量时序预测方法的精度更高；

2）使用GDCCN 能捕捉更加长的历史数据的非线性特征，一定程度上缓解了长程预测精度的下降；

3）GDCCN 的超参数选择十分重要，当沿用经典设置值时，模型的效果大打折扣；

4）使用DCGA 与SENet 相结合，从图数据的结构和属性两个层面进行动态拟合的效果要比单纯使用GCN的效果好.