计及马尔科夫链的能源社区产消者贝叶斯博弈策略

张 虹，孙书朋，李亚洲，孟庆尧，马泽群，刘 旭

（1.现代电力系统仿真控制与绿色电能新技术教育部重点实验室（东北电力大学），吉林吉林 132012；2.国网承德供电公司，河北承德 067000；3.大唐吉林发电有限公司长春第三热电分公司，吉林长春 130103；4.国网永康供电公司，浙江永康 321300）

0 引言

近年来，可再生清洁能源在电网中的占比日益增长[1]。越来越多的用电用户通过安装新能源发电设备，将自身角色转变为同时兼具生产和消费能力的产消者[2-3]。然而，由于产消者小而分散的特点，使其难以达到参与电力市场的门槛。为了整合过于分散的产消者资源，便于分布式能源就地消纳，以社区为单位对兼具生产和消费能力的社区用电用户进行研究，称之为能源社区产消者。与此同时，由此所引发的分布式可再生能源大量接入电网问题对于电力系统的安全稳定运行来说显得尤为重要。因此，能源社区产消者在社区内部进行能源交易，将分布式能源就地消纳，对于减少分布式能源频繁并网以及提高产消者的经济效益具有重要意义。

目前，国内外学者采用不同的预测方法对用户的决策行为进行预测分析。文献[4]针对电动汽车充电行为的决策问题，采用多维核密度估计和时间序列分析等方法进行预测分析。文献[5]售电商基于长短时记忆网络建立行为预测模型，对用户不同环境激励下的需求响应进行预测。文献[6]采用神经网络算法对光伏清洁能源输出功率进行预测，构建光伏清洁能源输出功率预测模型。然而，文献[4-6]中所提方法模型计算量较大，且需要较为精确的历史数据。为了减少计算量和对历史数据的依赖性，文献[7-8]利用马尔科夫链分别对储能功率和光伏电站出力进行预测分析。文献[9]通过马尔科夫决策对产消者负荷需求进行分析，进而计算最优交易价格。文献[10]采用马尔科夫链对住宅社区需求响应行为的概率特征进行描述，以降低社区能源消耗的成本。但是针对产消者交易身份不确定性的特性，能源交易过程中产消者的交易身份转换概率问题鲜有文献研究，未能充分考虑产消者参与电能交易的灵活性。

目前，博弈论[11-12]已被应用于分布式能源优化调度方面，用于解决能源交易问题[13-14]。文献[15-17]提出了运营商作为领导者，用户作为追随者的主从博弈模型，以促进两方收益的提升。文献[18]提出合作博弈机制，对产消者联盟的合作剩余进行公平分配。文献[19]建立演化博弈模型，实现产消者在多区域进行能源共享。以上论文均是围绕完全信息博弈理论进行研究，然而现实中一些博弈参与人的信息无法完全获知。因此，有必要研究参与人具有不完全信息[20]的博弈问题。文献[21]针对具有不完全信息的能源集线器，采用贝叶斯博弈方法对其进行建模分析。文献[22]将电动汽车的充放电成本建立为不完全信息，通过贝叶斯博弈方法优化社区间的能源消耗。然而，文献[20-22]针对贝叶斯博弈的研究，虽考虑了博弈参与人的不完全信息，但未对博弈参与人先验概率特征进行详细构建，难以确保不完全信息博弈中参与人类型的准确性。

根据目前研究的不足，本文针对产消者在能源交易过程中的身份转换问题，利用马尔科夫链构造其身份状态的概率特征，对其不同状态的可能性进行量化；针对产消者之间的能源交易问题，考虑产消者具有部分隐私信息问题，在能源社区内部通过贝叶斯博弈对交易过程进行优化，在保证了产消者隐私的情况下，提高其自身的收益。最后通过对含有多个产消者的能源社区为例进行算例分析，验证所提模型的有效性。

1 能源社区产消者能源交易框架

图1 为能源社区产消者能源交易模型框架。产消者包括光伏（Photovoltaic，PV），风力发电机（Wind Turbine，WT）、储能系统（Energy Storage System，ESS）和负荷。信息交互平台主要负责记录交易信息，不涉及功率交互。能源交易采用去中心化的点对点交易方式[23]，产消者在能源社区内部进行本地自主决策优化，信息交互主要通过信息交互平台进行，交易电量和价格通过贝叶斯博弈来确定。整个社区微电网通过一个公共连接点连接到配电网，与配电网进行能量交互。

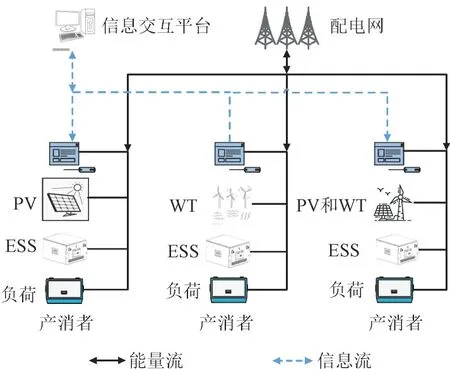
图1 产消者能源交易模型框架Fig.1 Framework of energy trading model for prosumers

能源社区产消者通过自身PV 或WT 产出电能，用以满足自身负荷需求，有能量剩余或缺额，与其他产消者进行社区内部能源交易。在此阶段，产消者首先通过信息交互平台查询历史交易信息，来预测其他产消者下一时刻身份状态概率分布，然后通过贝叶斯博弈模型求解出均衡解作为能源交易策略进行能源交易。若通过内部交易后仍有购售电需求或在某一时段选择不参与交易等情况，产消者可以利用ESS 进行充放电以实现自身功率平衡。

2 产消者身份状态马尔科夫链模型

在能源交易阶段，产消者交易身份具有不确定性，每个产消者都可以根据自己的需求和自身利益改变自己的身份，且某一时段的交易身份与前一天同一时段的身份状态有关。马尔科夫链对事物的状态的描述分析具备无后效性，与上述产消者的身份状态变化具有相同的特征。因此，可以采用马尔科夫链对产消者在能源交易过程中身份状态转换的概率进行分析。

在能源交易过程中，产消者可选交易身份共有出售、购买和不参与交易3 种，分别将其记为x1，x2和x3。因此，产消者在每一交易时段状态集合X均为[x1,x2,x3]。产消者i在t时段的状态转移概率表示为：

式中：p(Xi,t|Xi,t-1) 为产消者i在t-1 时段到t时段状态转移概率；Xi,t-1,Xi,t-2,...,Xi,0为初始时段至t-1时段状态所对应的状态空间。

相邻状态间的状态转移矩阵P∈R3×3表示如下：

其中，P中元素pmn表示产消者交易身份由t-1 时段状态pm转移到t时段状态pn的转移概率。矩阵中的元素满足2 个性质：1）每行的转移概率之和为1；2）下一时段状态只与当前时段状态有关，与过去其他时段状态无关。转移概率值可通过历史信息由极大似然估计法来确定，表示如下：

式中：hmn为历史数据中产消者身份状态由pm转移到pn的次数；hm为产消者身份状态由pm转移到其他状态的次数。

产消者i在t时段交易身份状态的概率为p(xi,t)，结合状态转移矩阵，产消者i在t时段的3 种交易身份状态概率集合表示为：

式中：p(Xi,t-1) 为产消者i在t-1时段每种状态的概率分布，其中列元素分别对应3 种状态可能发生的概率。

其他产消者通过产消者i的前1 d 的历史交易信息利用式（4）计算可以得到当前时段产消者i的状态信息，来选择自身在当前交易时段的状态。

3 产消者贝叶斯博弈模型

由于无法在交易之前获悉其他产消者的具体负荷用量及发电情况，也就无法确定产消者是否参与本次交易，即产消者的身份状态不能确定，这部分信息对于产消者来说属于私人信息。因此，本文采用贝叶斯博弈来描述考虑不完全信息的能源社区产消者间的能源交易行为。

3.1 产消者收益模型

3.1.1 目标函数

产消者i在能源交易过程考虑经济效益和环境效益，其每日收益函数表示如下：

式中：Ri,e为产消者i在能源交易中的经济效益；Ri,v为分布式能源就地消纳的环境效益；为产消者i储能充放电所需成本；T为优化调度时段，t=1,2,…,T。

产消者i在1 d 中的经济效益Ri,e表示如下：

式中：μi,t为产消者i在t时段购售电状态的系数，售电时为1，购电时为-1；分别为产消者i在t时段售电电价和购电电价；分别为产消者i在t时段售电电量和购电电量。

在能源交易过程中，在t时段产消者i为售电方时，其交易电价高于向电网售电电价，并且随着交易电量的增加，交易电价会逐渐提高；具体表示如下：

产消者i为购电方时，其他产消者为售电方，交易电价公式同理可得：

式中：-i为社区中除了产消者i以外的其他产消者；为产消者-i在t时段售电电价。

产消者通过新能源发电实现自发自用同时将剩余能量与其他产消者进行能源交易实现分布式能源就地消纳，减少碳排放量。因此，产消者i在1 d天中的环境效益Ri,v表示如下：

式中：r为碳排放权交易价格；ϖ为全国电网平均排放因子；为产消者i在t时段本地负荷功率。

储能充放电成本表示如下：

式中：cESS为储能系统运维成本系数；分别为产消者i的储能系统在t时段的充、放电功率。

3.1.2 约束条件

各产消者优化调度的约束条件主要有自身功率平衡约备约束、负荷约束、交易约束及储能设备约束等。

1）功率平衡约束为：

2）负荷约束为：

3）交易约束为：

对于交易价格和交易电量，应满足以下约束条件：

4）储能约束为：

在实际应用中，储能系统充放电及其容量应满足如下约束：

式中：Ei,t为产消者i在t时段所用储能容量；和分别为产消者i储能充、放电效率；分别为产消者i在t时段储能系统容量的最小值和最大值；Ei,0为产消者i储能每日初始容量；Ei,T为产消者i储能每日结束容量；为储能系统的充电状态，充电时为1，不充电时为0；分别为产消者i储能系统在t时段充、放电功率的最大值；分别为产消者i储能系统在t时段充、放电功率的最小值。

3.2 贝叶斯博弈模型

相较于具有3 个基本要素（局中人、策略集、收益）的完全信息博弈，贝叶斯博弈还需要引入博弈方类型和条件概率分布2 个要素。因此，一个完整的贝叶斯博弈描述为G={I,X,P,S,R}，其中的5 个元素分别为：参与人、类型空间、概率分布、策略空间及收益。

1）参与人：参与能源交易的社区产消者i。

2）类型空间X：为所有产消者类型的集合构成的类型空间，。产消者i的类型为xi∈Xi，Xi为产消者i所有类型的集合，共有3 个元素，对应于马尔科夫链中的3种状态，即|Xi|=3。

3）条件概率分布p(x-i|xi)，也称为信念，是产消者i的类型为xi的条件下产消者-i的类型为x-i的条件概率，产消者i在t时段的先验概率p(xi,t)即为式（4）马尔科夫链所求取的状态概率矩阵p(Xi,t)中的列元素。由于缺乏对其他产消者类型的了解，产消者i根据其类型的概率分布来推断其他产消者的类型。由贝叶斯公式可得：

式中：p(x-i,t,xi,t)为产消者i类型为xi,t及产消者-i类型为x-i,t同时发生的概率；为所有产消者-i类型为x-i,t和产消者i类型为xi,t的联合概率分布；X-i=X1×X2×···×Xi-1×Xi+1×···×XI为除了产消者i以外所有产消者的类型空间集合。

4）策略空间Si：为产消者i在自身类型集合下可以选择的全部策略，在本文中为产消者的交易电量。产消者所选择的策略受其类型所影响，不同的类型对应于不同的策略。一个不完全信息策略可以由不同类型组合对应的多个完全信息策略[24]表示，这些完全信息策略服从联合概率分布，表示为：

式中：si,t(xi,t)为产消者类型为xi,t时的策略。

5）收益Ri：为产消者i所有可选策略对应的收益集合。根据“海萨尼转换”[25]理论，贝叶斯博弈可以通过类型组合和相应的联合概率分布转化为完全信息博弈。因此，产消者的期望收益是这些完全信息博弈的所有收益的期望值，产消者i在t时段类型为xi,t的期望收益表示为：

式中：ERi,t(xi,t)为产消者i在t时段类型为xi,t的期望收益。

3.3 贝叶斯纳什均衡求解

在贝叶斯博弈中，产消者i根据其他产消者的策略来调整自身的交易策略，以最大化自己的收益，直到没有产消者愿意改变自身策略，即为纳什均衡。此时的产消者i策略为si,t*(xi,t)。

为了求得式（21）的纳什均衡解，可以将其转化为求解以下问题的全局最优解的最优问题：

对于式（24），贝叶斯纳什均衡解即为其全局最优解，因此，求解出纳什均衡解，即可得到产消者最优策略，进而求得最大收益。

因此，在贝叶斯博弈过程中，每个产消者都必须不断调整其策略，直到产消者之间达到纳什均衡。产消者i优化调度过程如图2 所示。图2 中n为常数，若n数值大于类型的数量|Xi|则结束循环，收敛判据为内点法中的对偶间隙小于误差，即Gap＜ε。

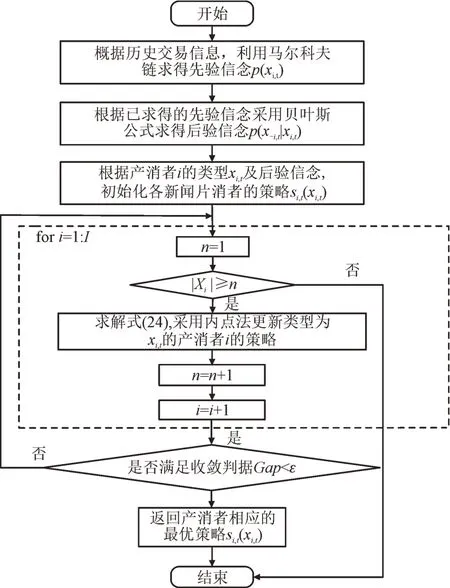
图2 产消者i优化调度过程Fig.2 Optimal scheduling process for prosumer i

4 算例分析

4.1 参数设置

本文对有10 个用户的新能源社区进行仿真分析，其中有6 个产消者配备了新能源发电装置，具体包括2 个安装光伏发电、2 个安装风力发电和2个同时安装光伏发电和风力发电，另外4 个为普通用电居民用户。每户产消者光伏设备装机容量约为25 kW。而对于小型风力发电设备，每户产消者装机容量为18 kW。优化调度时段为T=24 h，间隔周期Δt=1 h。

表1 中给出了不同时段电网的售电电价及上网电价。峰时段为：（11：00—13：00，18：00—20：00）；谷时段为：（23：00—次日6：00）；平时段为：除上述峰、谷时段外的其它时段。

表1 电网分时电价Table 1 Time-of-use price for power grid 元/kWh

产消者安装不同发电设备的电能产出时段具有功率互济的特点，相互之间进行能源交易具有可行性。图3 分别给出了每个社区产消者负荷与新能源发电情况，光伏出力及负荷数据来源于文献[26]。

图3 各产消者新能源出力情况Fig.3 Renewable energy output of each prosumer

4.2 优化调度结果分析

为验证本文所提模型的有效性，设定以下3 种算例：算例1，产消者直接与配电网进行交易，将所产出电能全额交易给配电网。算例2，产消者与其他产消者及用户通过传统的贝叶斯博弈进行电能交易，若有剩余或缺额，再与配电网进行交易。算例3，本文所提出的能源交易模型，产消者通过马尔科夫链对身份状态进行预测，然后与其他产消者及用户通过贝叶斯博弈进行能源交易，且每个产消者配备有储能装置，以满足自身功率平衡。

4.2.1 马尔科夫概率演化分析

图4 给出了某一时段产消者1 状态变化的马尔科夫链概率演化分析。产消者状态1 的概率由初始值0.2 逐渐演化为0.625，而状态2 的概率由初始值0.6 逐渐演化为0.312 5，通过不同状态的概率分布可以看出，这一时段产消者的交易身份由原来的状态2 转换为当前的状态1，即产消者身份状态实现了转变。因此对产消者状态进行概率演化分析可以预测产消者在下一时段的交易状态。将图4的结果作为先验概率，可以推导出贝叶斯博弈的联合概率分布，用于求解贝叶斯博弈的纳什均衡。

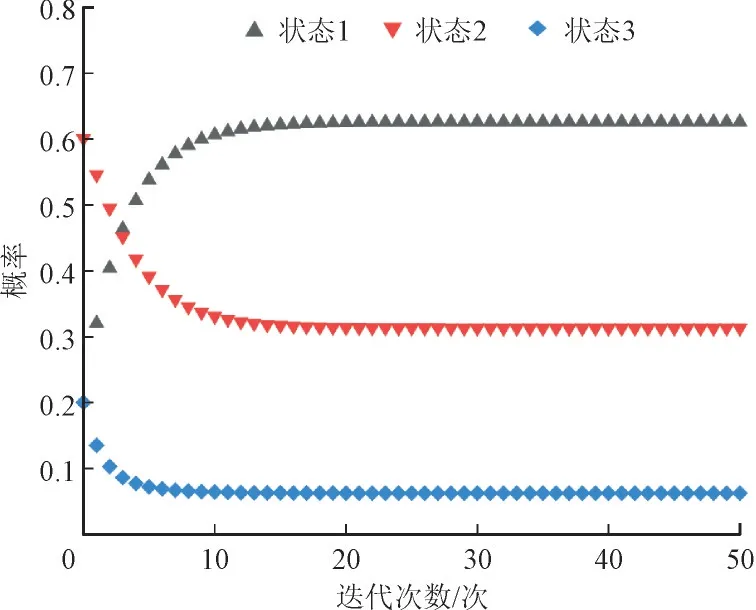
图4 产消者交易状态概率演化结果Fig.4 Diagram showing probability evolution of transaction status of prosumer

图5 给出了产消者1 在1 d 中各时段交易身份的预测状态与实际状态之间的对比。在图5 中给出的1 d 的24 个交易时段中，有2 个交易时段预测状态与实际交易状态存在差异，另外22 个交易时段预测状态均与实际交易状态相符，误差率小于10%。因此，说明采用马尔科夫链对产消者交易身份状态进行预测，预测结果准确率较高，能够满足预测期望，所提马尔科夫链身份状态预测模型能够在交易时段内有效预测产消者参与交易的身份状态。

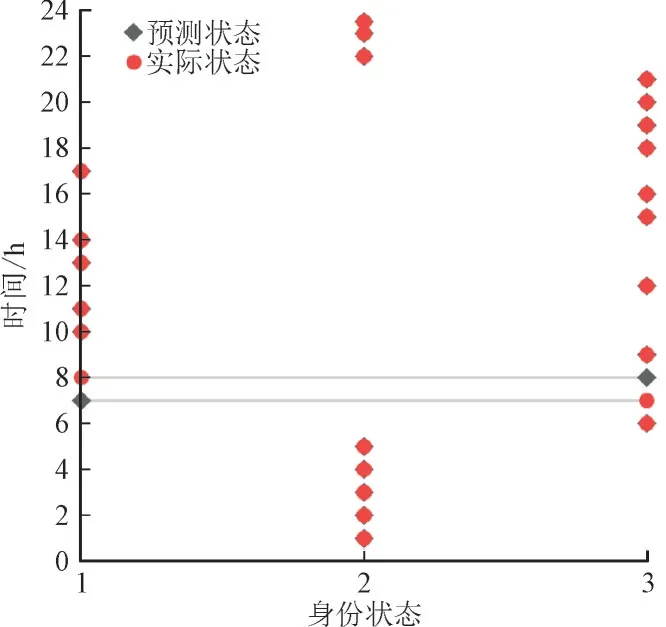
图5 产消者1预测状态与实际状态对比Fig.5 Comparison between predictive state and actual state of Prosumer 1

4.2.2 产消者能源交易调度结果

图6 给出了各产消者通过贝叶斯博弈进行能源交易的成交电量。其中，正值表示出售电量，负值表示为购入电量。图中其中部分时段产消者选择不参与能源交易，而是与自身储能系统进行充放电来满足自身功率平衡，这部分时段交易电量为0。

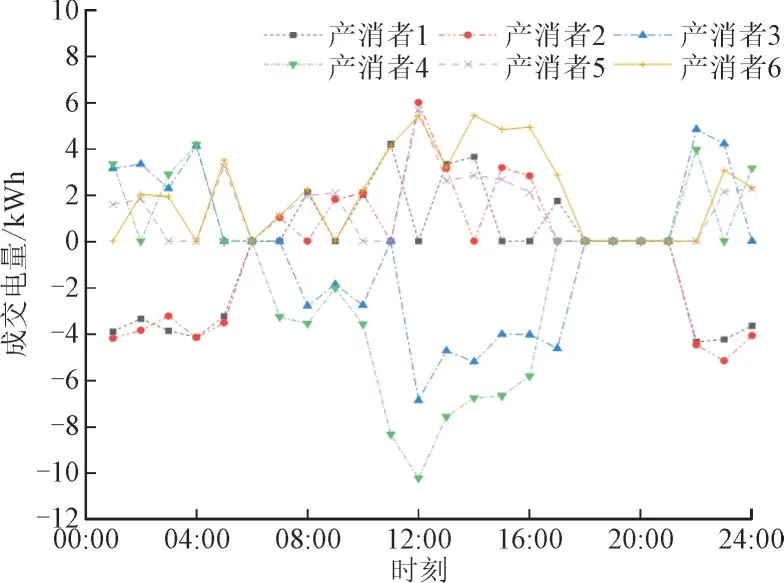
图6 各产消者博弈成交电量Fig.6 Transacted electricity quantity of each prosumer with game

对比产消者1 和产消者3 来看，由于产消者1安装光伏发电设备，白天发电量充足，产消者3 则安装有风力发电设备，在夜晚发电量较多，二者形成功率互济，说明相互之间进行能源交易具有可行性。同时，也更多地将新能源产出电能通过能源交易进行就地消纳，减少与电网进行能量交互的同时降低了弃风弃光率。

不同算例下产消者在1 d 中的买卖电价如图7所示。算例1 为电网售电电价，高于算例2 中的传统贝叶斯博弈交易电价和算例3 中的贝叶斯博弈交易电价，表明产消者有能量缺额时向电网购电所需成本较高，经济性较差。算例2 中的交易电价略低于电网售电电价，说明采用传统贝叶斯博弈进行能量交易经济性略优。算例3 中产消者通过贝叶斯博弈进行交易，并且产消者均安装了储能装置，在部分时段产消者通过与储能进行充放电来满足自身功率平衡所需。图中存在部分时段交易电价为0，其含义为在此时段产消者不参与能源交易，选择与储能进行充放电。

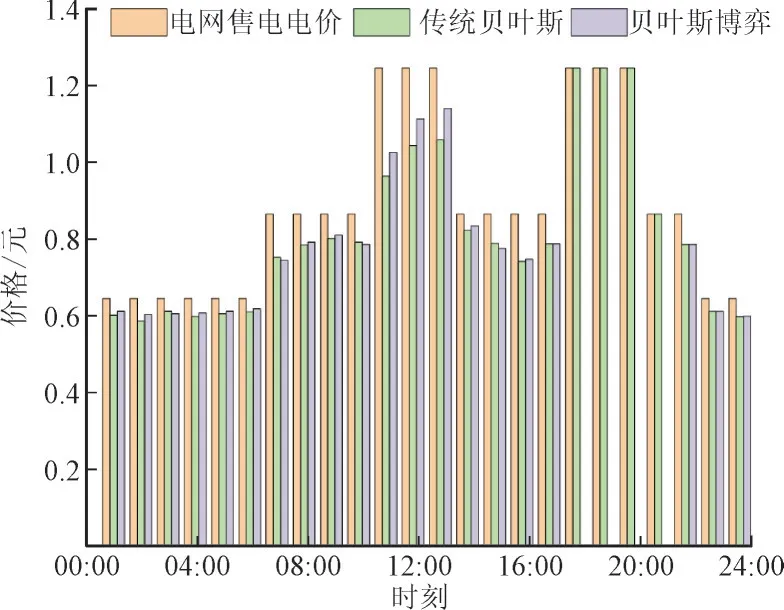
图7 不同算例下产消者的成交电价Fig.7 Transacted electricity price for prosumers in different examples

不计与储能充放电时段，算例3 中产消者1 天中共计20 个时段参与能源交易，其中有16 个时段算例3 中产消者的交易电价高于算例2 中产消者的成交电价，这部分交易时段约占总交易时段的80%。在13：00—14：00 期间，算例3 中的交易电价较算例2 中提高了约7.5%，这表明了采用贝叶斯博弈进行交易对于产消者售电的收益有所提高。

各产消者在不同算例下的收益对比如表2 所示。

表2 各产消者收益对比Table 2 Comparison of income among prosumers 元

算例1 中产消者全额与电网进行交易，对于电网调度压力较大，碳排放量较多，说明传统的交易模式不适用于分布式产消者消纳新能源，也不适应能源的低碳转型。算例2 中产消者通过传统贝叶斯博弈进行能源交易，交易剩余部分仍需与电网进行交易，实现了新能源部分消纳，减少了与电网交互次数。而在算例3 中，产消者安装有储能装置，能源交易剩余部分可以与自身储能进行充放电，与电网交互电量基本为零，表明可以将分布式能源进行全额消纳，大大减少了碳排放量的产生。

对比收益情况，以产消者2 为例，相比于算例1全额与电网进行交易，算例2 中采用传统贝叶斯博弈方法经济收益提高了53%。而相比于算例2，算例3 中产消者采用马尔科夫链对交易身份进行预测，产消者2 的经济收益提高了9.7%，由此可见，相较于传统的贝叶斯博弈，通过马尔科夫链对产消者身份状态进行预测，在提高贝叶斯先验概率准确性的同时，提高了产消者的收益。

表3 为各产消者在考虑环境效益下的综合收益。总的来看，以产消者1 和2 为例，二者之间环境效益相差不大，原因是环境效益仅与新能源发电量有关，产消者1 和2 均安装光伏设备发电，1 d 中发电量相差不大。因此，新能源发电量越大，环境效益越高。从表中可以看出，所有产消者总的环境效益之和为32.191 元，在综合收益中的占比为15.5%，经济效益占比84.5%。

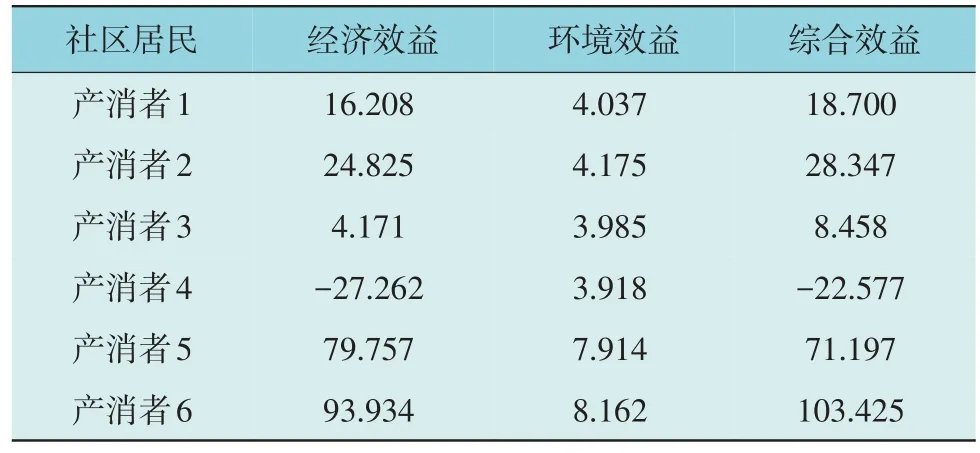
表3 综合收益Table 3 Comprehensive income of prosumers 元

5 结论

本文以兼具生产和消费能力的能源社区产消者为研究对象，针对产消者之间的能源交易，构建考虑马尔科夫链的贝叶斯博弈模型，并通过多个产消者之间的能源交易分析得出以下结论：

1）产消者在参与能源交易之前无法确定其他产消者的身份状态，通过马尔科夫链模型进行预测，从而确定其交易身份。全天预测准确率为92%，模型得到的概率分布更加符合实际情况，便于应用于实际电网调度中。

2）算例分析表明，采用本文所提出的贝叶斯博弈模型进行能源交易，最终获得的成交电量和成交价格均优于传统的贝叶斯博弈，产消者平均收益提高了30%。同时基本完全消纳了所产出的可再生能源，减少了产消者产生的碳排放量。

3）产消者在本文所提出的点对点能源交易机制下无需提供自身的新能源发电及负荷等隐私信息，仅需提供历史交易信息即可，充分保护了能源社区产消者的隐私性。

本文所建立的模型仅针对能源社区产消者为对象，下一步的研究将考虑针对微电网、区域综合能源等，对其所包含的不完全信息进行调度分析，可建立更全面的调度策略，以促进电力系统的总体优化。