构网型新能源场站环流产生机理研究

宋璐瑶，陈俊儒，程 静，陈雨田，张 龙，陈 军

（1.新疆大学，新疆乌鲁木齐 830000；2.国网新疆电科院，新疆乌鲁木齐 830000）

0 引言

为实现净零碳排放未来，人类正从传统化石能源向新能源转型[1-3]。随着光伏和风力等新能源发电技术不断进步，它们将逐步取代化石能源在电力系统中占据主导地位。新能源发电占比不断提高，日益减少对化石能源的依赖，但也为电力系统带来了低惯量低阻尼等一系列危害[4-6]。

目前，基于新能源并网控制技术主要分为跟网型（Grid-following，GFL）控制和构网型（Gridforming，GFM）[7-9]控制2 类。其中跟网型变流器对外表现为电流源特性，通过锁相环（Phase-locked Loop，PLL）跟踪电网相位。GFL 控制严重依赖PLL，若故障中PLL 失去跟随能力，电网暂态稳定性会降低[10]。构网型变流器对外表现为电压源特性，能够通过电力系统中功率同步环自行建立起系统的参考电压与相位[11-12]。此外，构网型变流器能够为电网提供惯量和阻尼，以支持高比例新能源渗透下电力系统的稳定运行[13-14]。

为增加电力容量，提高系统的可靠性和工作效率，新能源场站可运行在并联模式下[15-16]。在新能源场站并联系统中，2 个场站不同的输出电压幅值、相位、输出阻抗、载波相位和死区等都会产生环流。环流的存在导致系统损耗增加、效率降低，甚至导致电网崩溃[17-19]。

目前已经有了许多关于环流产生机理的文献。文献[20]在2 个三相电压源逆变器组成的系统中，从电压幅值不平衡与相角不平衡这两种情况对环流机理进行说明。文献[21]研究了当载波相位存在差异时环流的产生机理，并分析得到环流的表达式以及环流的特点。文献[22]将死区存在差异时对输出电压的影响作为一种谐波扰动，分析谐波扰动与系统传递函数的关系，从而建立起环流与死区差之间的关系，得到环流的表达式。文献[23]研究了虚拟同步机输出阻抗不一致导致并联虚拟同步机之间产生功率环流的问题。文献[24]说明了在电网不平衡时，并联系统中会同时出现正负以及零序的环流分量，并给出在不同旋转坐标下的环流控制策略。文献[25]通过分析2 台虚拟同步机并联模型，对下垂控制器进行小的修正以达到空载环流抑制的目的。

目前尚未有文章根据环流特征进行分类，从而无法捕捉到不同场景下环流的共性问题，增加了后续环流抑制的复杂性。为详细说明构网型新能源场站间环流的产生机理，本文将分为大信号环流和小信号环流2 部分进行详细阐述，为后续环流抑制工作提供有效指导。

1 环流的产生

为便于对环流产生机理进行详细分析，本文以图1 所示电路图来说明环流的产生：2 个构网型新能源场站并联，其发出20 Hz 的低频交流电通过低频交流线路、换流变压器后到达二极管整流站（Diode Rectifier Unit，DRU）。场站内变流器采用固定的低频20 Hz 来进行坐标变换。由于采用DRU模块，场站内功率环控制方式为：有功功率-电压（P-V），无功功率-相位（Q-δ）。

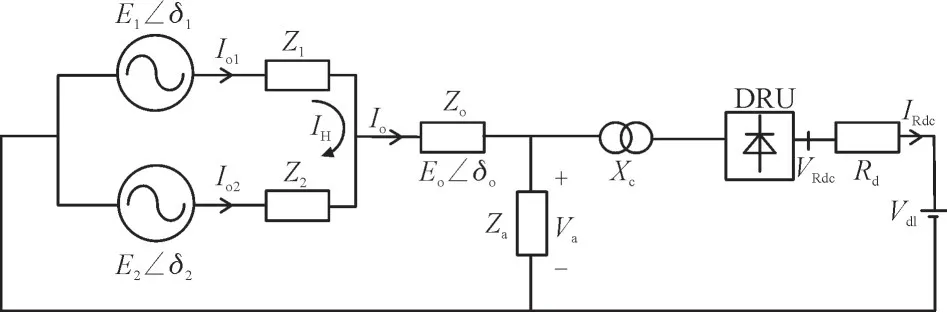
图1 环流机理分析等效电路图Fig.1 Equivalent circuit diagram for mechanism analysis of circulating current

图1 中，E1，δ1和E2，δ2分别表示2 个场站的输出电压幅值和相角，Z1=jωL1，Z2=jωL2表示每个场站的等效输出阻抗，L1和L2分别表示2 个新能源场站输出电感，Io1和Io2分别表示2 个新能源场站的输出电流向量，Zo为负载阻抗，Io为负载电流向量，uo为负载电压向量，δo为负载电压相角，IH为环流向量，Va为DRU 交流侧的交流母线电压向量，Za为环流通道阻抗，Xc为换流变压器漏抗，VRdc和IRdc分别为DRU 直流端电压和电流，VdI为直流电压源。

2 个场站的输出电流如式（1）所示：

定义环流IH如式（2）所示：

由式（2）可以看出，环流与2 个场站的输出电压的幅值、相位和输出阻抗密切相关。当其输出电压和阻抗相同时，不存在环流。若2 个场站输出电压幅值、相位以及输出阻抗存在差异，2 个场站之间会出现较大幅值的工频环流。将3 种条件下产生的环流定义为大信号环流。

当2 个场站逆变器的载波信号相位不平衡、死区存在差异或三相滤波电感参数不同，输出电压也会有所不同。从微观上来看，这3 种不平衡条件为2 个场站之间由于正弦脉宽调制（Sinusoidal Pulse Width Modulation，SPWM）或场站中电气参数存在微小差异从而导致产生了小幅值且具有谐波的环流，在此定义为小信号环流。第2 节和第3 节将分为大信号和小信号对环流产生机理进行详细阐述。

2 大信号下环流产生机理

考虑到所有可能的不平衡条件，即输出电压幅值不平衡、相位不平衡和输出阻抗不平衡去分析构网型新能源场站中环流的产生机理，在具体的数学分析过程中作非线性分析。

2.1 电压幅值不平衡

当2 个场站的参考有功功率不同时，由于采用P-V控制，其输出电压幅值将不平衡。假设本分析中输出相位和输出阻抗相同，可得环流如式（3）所示：

根据式（3），在电压幅值不平衡的情况下，2 台场站之间产生无功环流，其大小与2 个场站的电压幅值差成正比，与输出阻抗成反比。

2.2 相位不平衡

当2 个场站的参考无功功率不同时，其输出相位将不平衡。假设本分析中输出电压幅值和输出阻抗相同，可得环流如式（4）所示：

根据式（4），在相位不平衡的情况下，2 个场站之间主要产生有功环流，其大小与正弦相位角的差成正比，与输出阻抗成反比。

2.3 输出阻抗不平衡

当2 个构网型场站出口端线路长度不同时，其输出阻抗将不平衡。假设本分析中输出电压幅值和输出相位相同，可得环流如式（5）所示：

根据式（5），在输出阻抗不平衡的情况下，2 个场站之间将产生无功环流，其大小与阻抗的倒数差成正比。

3 小信号下环流产生机理

小信号主要引起三相电流不平衡以及SPWM的不同。在本节主要考虑了2 个构网型场站载波相位不平衡、死区不平衡以及三相滤波电感不平衡产生的环流，在数学分析过程中做线性化分析。

3.1 载波相位不平衡

当调制波相同，载波相位发生偏差时，将会影响SPWM 的生成，从而使开关管动作不一致，输出电压不同，导致产生高频环流。图1 中，令2 个新能源场站输出电感L1=L2=L，可得式（6）：

可得2 个场站之间环流变化量的斜率为(E1-E2)/2L。

图2 为调制波偏差电压示意图：将三角载波分别设为u1，u2，其相位差为θ，两载波相交点设为A，ωc，ωs分别为三角载波、调制波的角频率。M为调制比。设t1，t2，t3，t4分别为调制波与三角载波u1，u2上升段和下降段交点的时间。

图2 SPWM调制波偏差电压Fig.2 SPWM modulated wave deviation voltage

对Msin(ωst)＜A进行分析，当Msin(ωst)≥A时分析方法与Msin(ωst)＜A类似。在三角载波的第k个周期内，令调制波与载波相等得到调制方程，由调制方程可以得到正脉冲t4-t3、负脉冲t2-t1以及零脉冲t3-t2的宽度。

从图2 可以看出，当E1-E2为负脉冲时，环流的斜率为负，其大小为(E1-E2)/2L，反之，环流斜率为正，大小仍为(E1-E2)/2L。根据图2 可以得到正负脉冲宽度交替增大减小，在一个时刻2 个脉冲宽度相等之后，又开始进行交替，可以作出环流图像的上下包络线呈正弦变化，因此为了便于对环流进行分析，可以从数学角度将环流分解为下包络线与梯形分量之和。

令E1-E2=ud，结合式（6）以及1 个周期内的时间Δt=（t4-t3）-（t2-t1），可以得到A 相环流的下包络线表达式：

环流的梯形分量IHa2如图3 所示。

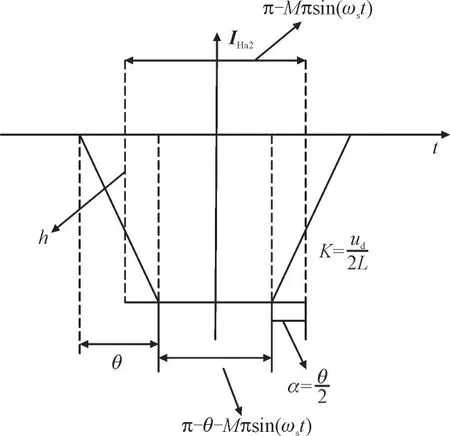
图3 环流梯形分量示意图Fig.3 Schematic diagram for trapezoidal components of circulating current

为了方便对环流的梯形分量进行分析，可以将其简化为环流矩形分量I′Ha2。环流矩形分量的宽度为π-Mπ sin(ωst)，高度为udθ/2Lωc。

对I′Ha2/(udθ/2Lωc)进行傅里叶分解及计算可得矩形分量的表达式为：

所以载波相位不同时，场站之间的环流可以表示为IH=IHa1+I′Ha2。

从式（7）和式（8）可以得到环流的直流分量为udθ/4Lωc。它与直流电压和载波相位差成正比，与输出电感和载波角频率成反比。将环流的下包络线与矩形分量中的基频分量相加可得环流中不存在基频分量。参考文献[21]通过对谐波分量进行研究，可以得到结论：谐波成分主要分布在角频率(nωc±kωs)处，且通过采用第n次Bessel 公式，将n分为奇数与偶数2 种情况，得到角频率(nωc±kωs)处的谐波振幅大小。

3.2 死区不平衡

新能源场站中的绝缘栅双极型晶体管（Insulate-Gate Bipolar Transistor，IGBT）上下开关管触发脉冲之前，进行一段时间的延迟来引入死区，可以避免电流过大或烧毁IGBT。将死区等因素所造成的SPWM波的偏差电压看作是一种谐波扰动[26]，在没有死区时系统传递函数的基础上，加入谐波电压的扰动，便可以得到谐波电压对场站输出电压带来的影响。与此同时，需保证场站中如滤波电感、电容等其他硬件参数相同。为便于分析，本文以2 台构网型逆变器为例，得到死区对输出电压的影响，同时采用电压电流双环控制，对死区产生的环流具有一定的抑制作用。1 台逆变器系统传递函数如图4 所示。

图4 系统传递函数Fig.4 System transfer function

令G1=GV，G2=GIGPWMKb，G3=1/sL，G4=1/sC。

分别对3 个输入求传递函数：

令2 台逆变器参考电压相同，2 台逆变器的输出电压相减可得：

令ue1-ue2=Δue，并结合式（1）、式（2）和（11）：

式中：Z为逆变器输出阻抗，且2 台逆变器输出阻抗Z1和Z2相同，即：Z1=Z2=Z。

由式（12）可以得到，若构网型场站参考电压相同，硬件电路参数一致的情况下，死区的差异会使两者之间存在电压差，环流的大小与死区的电压差成正比，电压差越大，环流越大。

3.3 三相滤波电感不平衡

由于工艺水平不够成熟以及环境的复杂，场站中硬件参数可能会存在差异，场站中每台机组的三相滤波电感不能够保证完全相同，这就容易使输出三相电压电流不平衡。为便于说明三相滤波电感不平衡对机组输出的影响，本节以2 台逆变器并联为例进行数学分析。由于滤波电感在环流通路上，不可避免的会对环流产生相应的影响。图5 为2台并联三相逆变器的拓扑结构。

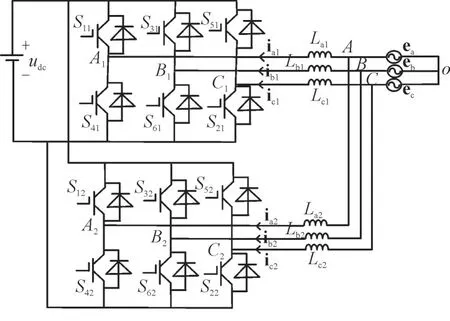
图5 2台并联三相逆变器的拓扑结构Fig.5 Topology of two parallel three-phase inverters

图中，udc为逆变器直流侧电压，设第n个模块的开关管为Skn（k=1，2，3，4，5，6），ijn（j=a，b，c）为电感电流向量，Ljn为每相输出电感，ej为相电压，o为公共连接点。

当电网三相平衡时，电压电流中只存在正序分量。当电网三相不平衡，除了正序分量，还有负序分量和零序分量的存在。用三相对称分量法对电网三相不平衡状态进行数学分析。设逆变器输出三相电压为Uoa，Uob，Uoc，将其分解为正序、负序、零序的叠加可得：

正序，负序分量三相对称，但其相位相反，零序分量三相相位相同。在实际控制中，一般采用在正序同步坐标系下将交流量转化为直流量经过比例积分（Proportional Integral，PI）控制器进行控制，将式（13）经过派克变换转为dq坐标系：

由式（14）可知，经过派克变换之后正序电压与ω无关，表现为直流分量，负序电压体现为二倍频分量。由于PI 控制不能对交流量进行无静差控制，因次需要对负序分量进行抑制。

在电网三相不平衡时，需要采用一定的控制策略达到三相平衡，才能保证系统的稳定运行，最终达到输出电压平衡的目的。此时，三相电压平衡，而三相电流不平衡。结合逆变器输出瞬时有功功率以及无功功率表达式可得：

由式（15）可知：在三相电网不平衡状态下，有功功率和无功功率均由直流分量和二倍频分量两部分组成。其中直流分量是由正序电压和正序电流共同作用的结果，而二倍频分量是有正序电压和负序电流共同作用的结果，零序电流分量与正序电压作用并不产生功率，这是因为正序电压三相对称而零序电流三相相位相同。相对于正序环流和负序环流，零序环流的分量远远低于正、负序环流，因此不再考虑零序电流分量。

4 大信号下环流机理的仿真结果

为了方便分析验证构网型新能源场站在大信号下的环流产生机理，以图1 作为拓扑结构，在MATLAB/Simulink 搭建了2 台逆变器的测试模型。仿真参数如表1—表3 所示。

表1 低频交流线路仿真参数Table 1 Simulation parameters of low-frequency AC line

表2 逆变器组仿真参数Table 2 Simulation parameters of inverter sets

表3 整流器侧DRU仿真参数Table 3 Simulation parameters of rectifier side DRU

4.1 电压幅值不平衡仿真结果

当2 台构网型逆变器的有功功率输出不平衡，而输出无功功率和阻抗保持平衡时，2 台逆变器输出电压幅值变得不平衡。图6 显示了电压幅值不平衡仿真结果，其中2 台逆变器的初始功率都是2 MW，而第2 台逆变器在3 s 时将其输出功率提高到4 MW。

图6 电压幅值不平衡仿真结果Fig.6 Simulation results of voltage amplitude imbalance

在图6 中，P1，P2和PT分别表示第1 台逆变器、第2 台逆变器及变压器侧输出有功功率。从图6 中可以看出，在平衡态开始时，2 台逆变器的输出电压幅值与其输出功率相同。而在第2 台逆变器将其功率提高到4 MW 后，其输出电压增加并打破了系统平衡。如图6（b）所示，无功功率输出在第2台逆变器中增加而在第1 台逆变器中减少，说明2台逆变器之间产生了无功环流，验证了2.1 中的理论分析，同时由仿真结果可得无功环流从较高的逆变器输出电压到较低的逆变器输出电压。

4.2 相位不平衡仿真结果

当2 台构网型逆变器的输出相位角不平衡，而输出电压幅值和阻抗保持平衡时，图7 显示了相位不平衡的仿真结果，其中2 台逆变器都具有相同的初始相位角，第1 台逆变器在3 s 时将其输出相位角从π/2 减小到π/3。

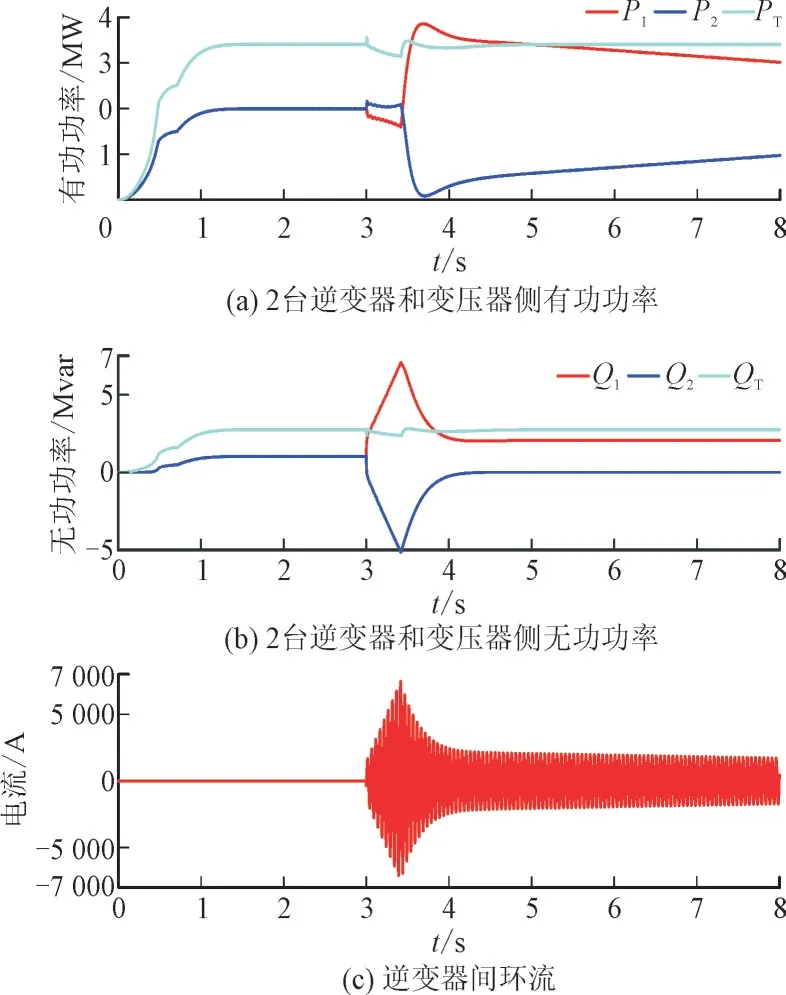
图7 相角不平衡仿真结果Fig.7 Simulation results of phase angle imbalance

从图7 中可以看出，逆变器的输出无功功率在平衡状态开始时是相同的。第1 台逆变器降低其相角后，打破了系统平衡。如图7（a）所示，第1 台逆变器中的有功功率输出减小，第2 台逆变器输出有功功率增加，说明2 台逆变器之间产生了有功环流，验证了2.2 节中的理论分析，同时由仿真结果可得有功环流从具有较高相位角的逆变器到较低相位角的逆变器。

4.3 输出阻抗不平衡仿真结果

当2 台逆变器输出功率也即输出电压幅值平衡，而输出阻抗不平衡时，图8 显示的是第1 台逆变器输出阻抗为20×10-3mH，第2 台逆变器输出阻抗为10×10-3mH 的仿真结果。

图8 输出阻抗不平衡仿真结果Fig.8 Simulation results of output impedance imbalance

如图8（b）所示，第1 台逆变器无功功率输出增加，在第2 台逆变器无功功率输出减少，表明2 台逆变器之间产生无功环流，验证了2.3 节中的理论分析，同时由仿真结果可得无功环流从具有较高输出阻抗的逆变器流向较低输出阻抗的逆变器。

4.4 载波相位不平衡仿真结果

由于整个系统都在20 Hz 的低频下工作，因此以20 Hz 为基本频率，载波频率设定为10 000 Hz，作出载波相位差为π/4，π/2 和π 时环流的快速傅里叶变换（Fast Fourier Transform，FFT）分析如图9所示，THD 代表环流的谐波失真。

图9 载波相位不同步时环流的FFT分析Fig.9 FFT analysis of circulating current when carrier phase is out of synchronization

将由图9 可以看出环流存在直流分量，并且谐波阶次分布在500 附近和1 000 附近，即谐波频率分布在10 000 Hz 与20 000 Hz 附近，验证了3.1 节理论分析中所说明的环流存在直流分量以及谐波成分主要分布在频率(nωc±kωs)。对比图9（a）、图9（b）和图9（c）可以看出，随着载波相位差的增大，谐波所占的百分比也在增加。

4.5 死区不平衡仿真结果

为了观察死区的加入对环流造成的影响，分别对2 台逆变器加入死区，设置3 组不同的实验对理论分析进行验证：（1）2 台逆变器均无死区；（2）2 台逆变器死区均为1 μs；（3）第1 台逆变器死区为1 μs，第2 台逆变器死区为3 μs。死区不平衡实验结果如图10 所示。

图10 不同死区差逆变器间的环流Fig.10 Circulating current between inverters with deadzone difference

由图10（a）可得2 台逆变器均无死区时，2 个场站之间的环流幅值小于10，当2 台逆变器都加入了1 μs 的死区后，环流谐波增大。由图10（c）可以看出，死区差增大，环流波形越嘈杂，震荡越剧烈，谐波含量越高，验证了3.2 节中的理论分析：环流的大小与死区的电压差成正比，电压差越大，环流越大。

4.6 三相滤波电感不平衡仿真结果

将2 台逆变器的滤波器电感设为三相不平衡电感，第1 台逆变器滤波器的a 相电感设为7×10-4mH，b 相和c 相设为1×10-4mH，第2 台逆变器的a 相电感设为3×10-4mH，b 相和c 相设为1×10-4mH。三相滤波电感不平衡仿真结果如图11 所示。

图11 三相滤波电感不平衡仿真结果Fig.11 Simulation results of three-phase filter inductance imbalance

图11 作出了第1 台逆变器输出电流、功率以及2 台逆变器之间的环流波形图。当三相滤波电感不平衡时，由图11（a），（b）可得逆变器输出电流不平衡，第2 台逆变器输出电流特点与其类似，因此不再作图说明。通过对逆变器输出有功功率以及无功功率的测量，可得其波动主要为二倍频波动，验证了三相滤波电感不平衡时负序分量会产生二倍频分量的结论。图11（c）证明了当三相滤波电感不平衡时，2 台逆变器之间会产生环流。

通过对2 个场站进行输出电压幅值、相角、输出阻抗、输出载波相位、死区以及三相滤波电感不平衡的仿真，可以总结出大信号下的环流具有大幅值、呈基频振荡的特点，小信号下的环流具有幅值小且含有大量谐波的特点，这些特点为后续环流抑制方式奠定了基础。

5 结语

本文针对构网型新能源场站内环流问题，以大信号下电压幅值不平衡、相位不平衡和输出阻抗不平衡以及小信号下载波相位不平衡、死区不平衡和三相滤波电感不平衡为场景，分析6 种场景下的环流产生机理，得到各场景下的环流特点：大信号下的环流为工频振荡且幅值较大；小信号下的环流含谐波分量且幅值较小。本文构网型新能源场站环流产生机理的研究为后续环流抑制策略奠定基础。