基于ARIMA 预测优补化货模策型略的研生究鲜类商品自动定价与——以蔬菜类商品为例

聂宇旋

(云南大学软件学院 云南昆明 650504)

1 引言

生鲜超市管理领域涉及供应链管理、定价策略及市场需求分析等重要问题。以蔬菜类商品为例，这些商品在生鲜商超中具有较短的保鲜期，其品质随着销售时间的推移而逐渐降低。如果商品当日未售出，次日销售将变得更加困难。因此，商超通常会根据具体情况进行每日补货。由于商超销售的蔬菜品种繁多，产地多样化，而且蔬菜的采购通常在凌晨三四点进行，使得商家必须在不完全了解特定单品和采购价格的情况下，制定当日各蔬菜品类的补货决策。一般而言，蔬菜的定价采用“成本加成定价”方法，商超通常会对由于运输损耗和品质下降而受影响的商品进行打折销售[1]。

在这个过程中，可靠的市场需求分析显得尤为重要。从需求方面来看，蔬菜类商品的销售量通常与时间存在一定相关性；从供给方面来看，4—10月期间蔬菜供应的品种相对较多，但由于商超的销售空间受限，因此制定合理的销售组合变得至关重要。在制定补货和定价决策时，商超需要对市场需求进行深入分析，确保能够满足消费者的需求，同时实现利润最大化。

2 商品销售量分布规律及相互关系

2.1 蔬菜品类销售量分布规律

根据某生鲜商超各蔬菜品类的商品信息、各蔬菜品类的销售与批发相关数据可获取蔬菜各品类的销售情况(见图1)。由蔬菜各品类的销售情况可以得知，蔬菜各品类中销量分布规律为：花叶类销售量最大，其次是辣椒类、食用菌，水生根茎类和花菜类的销售量几近相等，茄类的销售量最低。

图1 蔬菜各品类销售量分布

调查发现，销售量和销售定价之间存在一定的关系，即销售单价较低的蔬菜品类往往能够吸引更多消费者，从而实现较高的销售量和销售总价。在商超制定补货和定价策略时，考虑到季节因素势必对销售产生影响，因此以季度为周期，统计了如图2所示的蔬菜各品类的平均销售单价的变化趋势。由图2可知，蔬菜各品类利润变化与销售总价的变化大致相同，花叶类蔬菜的售卖由于销售量大，给商超带来的利润最多，其次是辣椒类和食用菌，茄类、花菜类和水生根茎类的利润大致相同。

图2 蔬菜各品类平均销售单价变化趋势

2.2 蔬菜各品类销售量的皮尔逊相关性分析

以季度为周期，我们利用皮尔逊相关系数计算蔬菜各品类销售量之间的关联关系，皮尔逊相关系数的计算方式如下[2]：

式(1)中：Xi和Yi是两个变量X和Y观测值和分别是X和Y的均值，n是观测值的数量。

根据式(1)可对蔬菜各品类销售量之间的相关性进行求解分析，得到如图3所示的销售量相关系数矩阵。相关系数矩阵是一个方阵，其中每个元素是两个变量之间的相关系数。在这个热力图中，每个单元格的颜色表示对应品类之间的相关系数大小，颜色越深表示相关性越强，颜色越浅表示相关性越弱。根据相关系数矩阵，我们可以看到不同蔬菜品类之间的相关性强弱不同，其中花叶类和茄类之间的相关性较弱，而花叶类和辣椒类之间的相关性较强。此外，水生根茎类和茄类之间的相关性也相对较弱[3]。

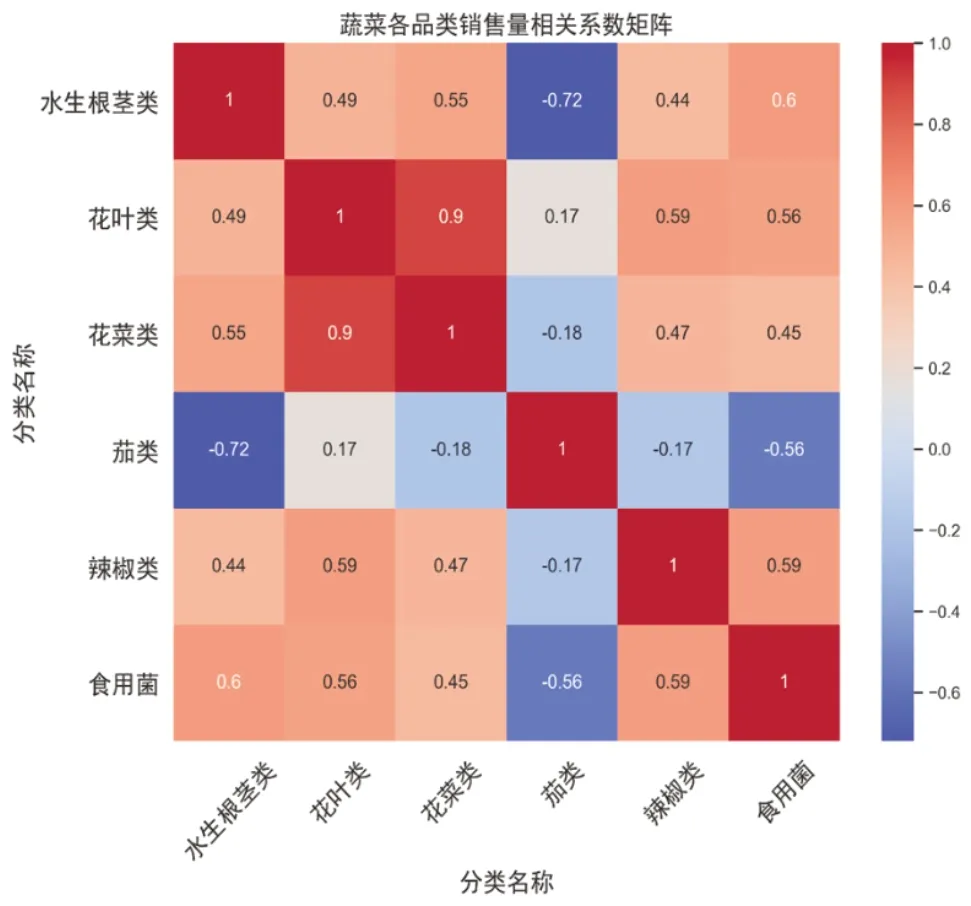
图3 蔬菜各品类销售量相关系数矩阵

不同的蔬菜品类具有不同的蔬菜单品，各个单品之间销售量的相关性也是制定蔬菜单品补货和定价策略的重要影响因素，因此求解得到如图4所示的各个蔬菜单品销售量相关系数矩阵。

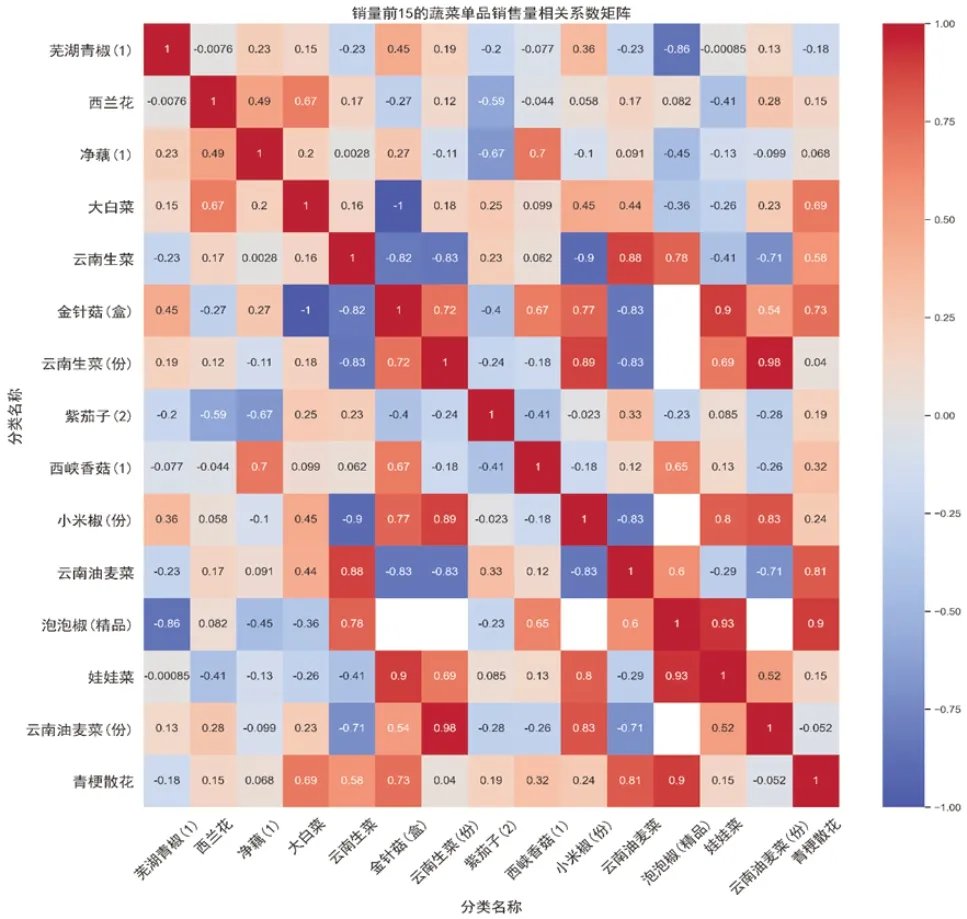
图4 单品销售量相关系数矩阵

由图四可知以下几种蔬菜单品之间的相关性关系，如云南生菜和云南油麦菜之间的相关系数为0.883445，相关性较强；云南生菜和金针菇(盒)之间的相关系数为0.724516，相关性较强；云南生菜和泡泡椒(精品)之间的相关系数为0.778169，相关性较强；云南生菜和云南生菜(份)之间的相关系数为-0.831510，呈现负相关性；大白菜和金针菇(盒)之间的相关系数为-1.000000， 呈现负相关性。当大白菜和云南生菜的销售量增加时，金针菇(盒)与云南生菜(份)的销售量会相应受到影响而下降。

3 蔬菜各品类的补货和定价模型

3.1 销售总量与成本加成定价的关系

考虑到不同函数用于拟合不同的蔬菜品类平均销售定价与销售总量的关系，包括线性函数、幂函数和对数函数，并选择拟合效果最佳的模型作为定价—销量模型展示了不同函数对六种蔬菜品种的拟合效果(见图5)，最终选择的最佳模型参数数据如表1所示。

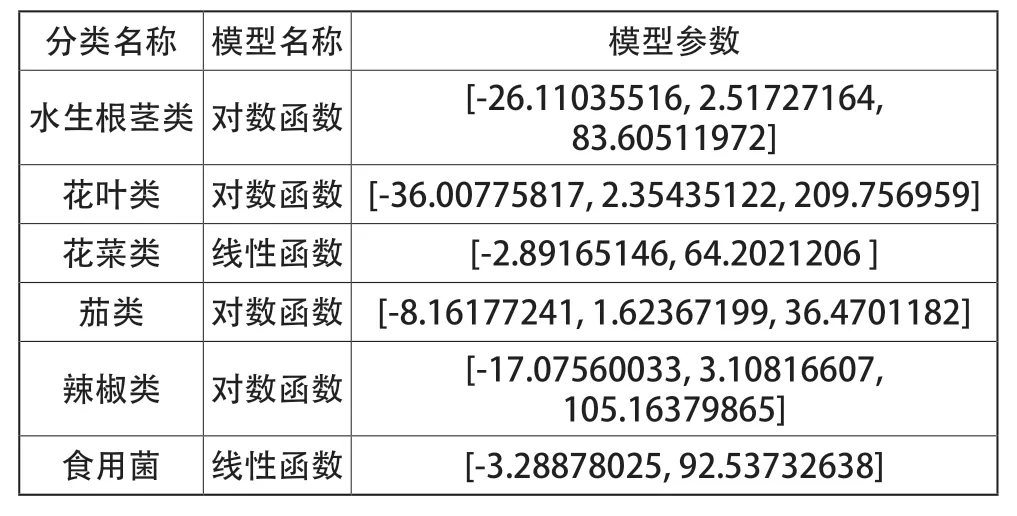
表1 最佳模型参数

图5 蔬菜品类平均售价与销售量的关系拟合曲线

3.2 ARIMA预测模型建立

为了获取商品利润，还需要对蔬菜品类的平均批发价进行预测，本文利用ARIMA模型对蔬菜品类未来7天的平均批发价进行预测(以花叶类商品为例)。ARIMA模型基于时间序列数据中的趋势和周期性，通过对数据进行自回归、差分和移动平均的操作进行捕捉和建模[4-5]。利用模型的AIC准则(Akaike Information Criterion)选择最佳的模型参数为(2，2，2)，对未来七天的蔬菜品类平均批发价格进行预测，预测结果如图6所示。

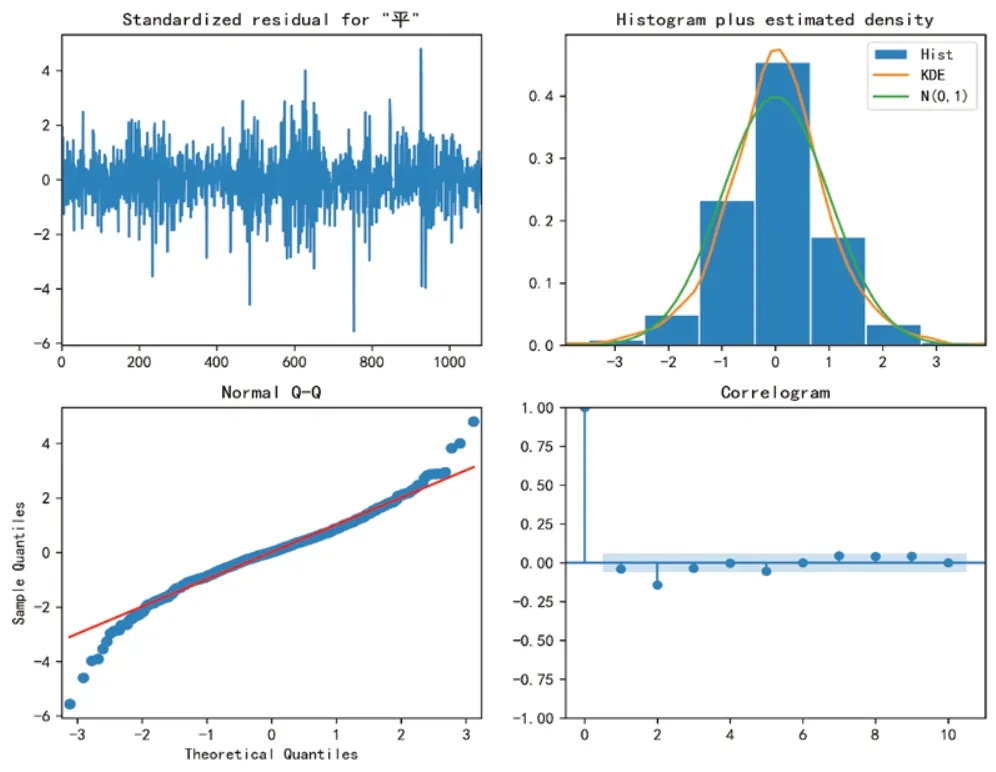
图6 花叶类ARIMA预测模型

3.3 最佳补货总量和定价策略求解

得到蔬菜品类平均批发价格和定价—销售量模型及各品类ARIMA模型后，构建出非线性规划模型，以求解最佳的补货总量和定价策略。所构建的非线性规划模型如下：

其中，目标函数为最大化商超第x天在蔬菜品类i上的利益，含义为销售总价批发总价，supplyi,d为商品i在x天的补货量，salei,x为商品i在x天的销售量；约束函数(3)为补货量大于销售量加损耗量，约束函数(4)为销售价大于成本批发价，约束函数(5)为补货量和销售定价大于0，约束函数(6)为定价—销售量函数，通过该函数可由销售定价确定销售量，带入数据，求解得到商超未来7天的蔬菜品类日补货量和定价策略如表2所示。

表2 未来7天日补货量和定价策略

4 蔬菜各品类的补货和定价模型

实际在商超补货时，由于蔬菜类商品的销售空间有限，每天能够出售的单品数量有限，蔬菜单品每次订购也有最小订购量的限制，所以考虑实际情况，我们需要得到单品的补货和定价策略，在满足市场各类蔬菜商品需求的前提下，使得商超收益最大。

先假设约束条件为单品订购最小需满足2.5kg，可售单品总数为27～33个。

为满足约束条件单品订购满足2.5kg，需对数据进行清洗。由于大部分蔬菜隔日变质无法出售，因此可建立损耗率与保鲜期的关系来剔除不满足约束条件的单品，可在阈值T=2.5的情况下，补入平均每日销量较小的蔬菜单品。

对数据处理的损耗率均值为 9.43%，标准差为 0.052，建立如下模型：

其中，Loss_rate 为蔬菜单品损耗率，Loss_ratem为单品平均损耗率，expirationdate为修正后的保鲜期。修正后的保鲜期可直接作用在每日平均销售量上，即保鲜期×每日平均销售量＞T。

总利润计算公式为：

基于贪心策略，在满足约束条件的情况下，尽可能向背包内装入单位利润高的单品[6]，流程如图7所示。本文首先计算了各蔬菜单品的利润，并进行了排序，对蔬菜单品进行初步筛选，可知满足单品陈列量不小于2.5kg的单品种类只有29种。此时单品已满足基本约束条件，即可售单品总数在27～33个，单品陈列量不低于2.5kg，满足各品类蔬菜均有陈列。为保证总收益最大，再根据贪心法则，优先选择日平均利润大的单品。在品类为背包的情况下，各品类的单品独立计算装填6个背包，即可得到蔬菜单品的最优补货和定价方案。

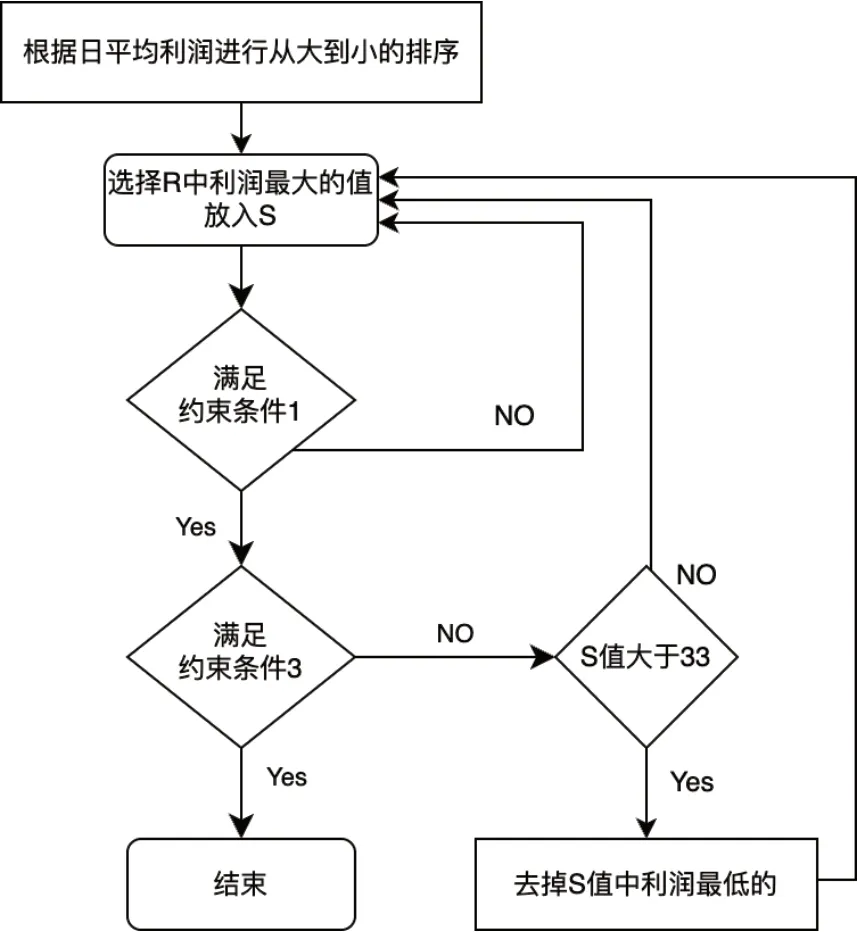
图7 贪心选择策略流程框图

5 结语

为保障生鲜市场持续稳定发展，本文建立了综合评价模型帮助商超做出最大收益化的蔬菜类商品自动定价与补货策略，根据商超市场的实际情况预测销售趋势、合理制定价格策略，以及有效制定补货计划。首先，对蔬菜各品类和单品的各项数据均以季度为周期进行分析，利用皮尔逊相关系数计算蔬菜各品类销售量之间的关联关系，以相关系数矩阵热力图展现蔬菜各品类及单品销售量的分布规律及相互关系；其次，分别用线性函数、对数函数、幂函数对蔬菜各品类销量与成本加成定价的关系进行函数拟合，并通过平均销售量与平均销售价散点图和拟合优度，发现花菜类与食用菌的成本加成定价与销售总量呈线性关系，水生根茎类、花叶类、茄类、辣椒类的成本加成定价与销售总量呈对数关系，再建立关于日销量和批发价的规划模型，目标函数为各品类最大日收益，决策变量为各品类日补货量和定价策略，使用拟合的回归方程预测日销量，并结合ARIMA模型预测求得最优补货量和定价策略；最后，为了增加模型的适用度，考虑销售空间和各单品订购量满足最小陈列量，建立背包模型。在满足题目其他约束条件下使用贪心算法向背包内装入单位利润高的蔬菜，求得每个单品的最佳补货量和定价策略，使商超在未来某一天实现最佳盈利。