GLOBAL SOLUTIONS TO 1D COMPRESSIBLE NAVIER-STOKES/ALLEN-CAHN SYSTEM WITH DENSITY-DEPENDENT VISCOSITY AND FREE-BOUNDARY*

(丁时进) (李颖花) (王喻)

School of Mathematical Sciences, South China Normal University, Guangzhou 510631, China E-mail: dingsj@scnu.edu.cn; yinghua@scnu.edu.cn; yuwang@m.scnu.edu.cn

Abstract This paper is concerned with the Navier-Stokes/Allen-Cahn system, which is used to model the dynamics of immiscible two-phase flows.We consider a 1D free boundary problem and assume that the viscosity coefficient depends on the density in the form of η(ρ) = ρα.The existence of unique global H2m-solutions (m ∈N) to the free boundary problem is proven for when 0 ＜α ＜ Furthermore, we obtain the global C∞-solutions if the initial data is smooth.

Key words Navier-Stokes/Allen-Cahn system;density-dependent viscosity;free boundary;global solutions

1 Introduction

In[1], Blesgen proposed a diffuse interface model for macroscopically immiscible two-phase flows.Compared with the classical sharp interface models, this can naturally describe topological transitions on the interface, such as droplet formation, coalescence or the break-up of droplets.A phase field variableφwas introduced to describe the interaction between two fluids.This model couples together Navier-Stokes equations and Allen-Cahn equations, and has been widely accepted and successfully used in numerical simulations [15, 28].

It is well known that the Navier-Stokes equations can be derived from the Boltzmann equation through a Chapman-Enskog expansion to the second order [13], where the viscosity coefficient depends on temperature.For the isentropic case, this dependence is transferred into the dependence on the density by laws of Boyle and Gay-Lussac for an ideal gas [22].From the deduction of the compressible Navier-Stokes/Allen-Cahn equations [1, 10, 16], we can see that the viscosity also depends on the density.In this paper, we consider the 1D compressible Navier-Stokes/Allen-Cahn equations with density-dependent viscosity and free boundaries

for(y,τ)∈(a(τ),b(τ))×(0,+∞),whereρ,uandφrepresent the total density,the mean velocity field and the concentration difference between two fluids, respectively.Moreover,μdenotes the chemical potential, the positive constantδis related to the thickness of the interfacial region,ηis the viscosity coefficient, and the pressure isP(ρ) =Aργwithγ ＞1.Without loss of generality, we assume thatA=δ= 1.Here,a(τ) andb(τ) are the free boundaries satisfying that

We supplement system (1.1) with the initial and boundary value conditions

Moreover, we assume that the viscosity is of the form

where ～ηis a positive constant.

In recent years, the compressible Navier-Stokes/Allen-Cahn system has attracted much attention on account of its distinct physical background, and there have been many valuable investigations of it.Here we recall some results on the 1D compressible NSAC system that are closely related to our study.For the initial boundary value problem (IBVP), for when the viscosity is assumed to be a constant, Ding-Li-Luo [8] and Chen-Guo [2] proved the global strong solutions both without a vacuum and with a vacuum.Later, Zhang [32] improved the regularity, and obtained theHi-solutions (i=2,4).Meanwhile, Chen-Zhu [3] assumed that

and proved the global existence of strong solutions for when 2≤α ≤γ,β=0, and established blow-up criteria for strong solutions for whenβ ≥1 with a vacuum.Under the hypothesis that

where ～ηis a positive constant, Su [25] established the existence of strong solutions.For 1D compressible NSAC equations with free boundary conditions, Ding-Li-Tang [9] considered a constant viscosity case, proved the existence and uniqueness of local solutions by using the Schauder Fixed Point theorem,and then extended the local solution to a global one by attaining global energy estimates.For when the viscosity depends on the density as

and the initial data is connected to a vacuum continuously, Li-Yan-Ding-Chen [20] obtained the existence of weak solutions by a line method.

For 1D non-isentropic NSAC equations, Chen-He-Huang-Shi [4, 5] simplified the original model and proved the existence of unique strong solutions to the 1D IBVP and the Cauchy problem with a constant viscosity and temperature-dependent heat conductivity

whereβ ＞0.Yan-Ding-Li [27] considered the phase variable dependent viscosity and the temperature-dependent heat conductivity

whereβ ＞0.They obtained the well-posedness of strong solutions under the hypothesis thatα ≥0 is small.Recently, Dai-Ding-Li [6] studied the density-dependent viscosity and the temperature-dependent heat conductivity

We will prove the existence and uniqueness ofH2-solutions, then improve these intoH2m(m ∈N)-solutions andC∞-solutions.Obviously, system (1.5) is of strong coupling and strong nonlinearity, and degeneracy will appear near the vacuum state.In addition, although Liet al.[20] dealt with the case of when the initial data is connected to a vacuum continuously, they only obtain the existence of weak solutions, and not the uniqueness.At the cost of the free boundary jump to the vacuum,we can study the case where the viscosity is proportional to the density, and obtain the uniqueC∞-solutions.

We now give the definition of anHi-solution.

Definition 1.1For any fixed constantT ＞0,(ρ,u,φ)is called a globalHi([0,1])-solution(i=2m) to problem (1.5)-(1.7) if it satisfies the condition (1.6) and that

We now state our main results.

Theorem 1.1If the initial data (ρ0,u0,φ0) is compatible with the boundary conditions and satisfy (A1), (A2), then problem (1.5)-(1.7) admits a unique globalH2-solution (ρ,u,φ)on [0,1]×[0,T].

Theorem 1.2If the initial data (ρ0,u0,φ0) is compatible with the boundary conditions and satisfy (A1), (A4), then problem (1.5)-(1.7) admits a unique globalH2m(m ∈N)-solution(ρ,u,φ) on [0,1]×[0,T].

Theorem 1.3If the initial data (ρ0,u0,φ0) is compatible with the boundary conditions and satisfy (A1), (A5), then problem (1.5)-(1.7) admits a unique globalC∞-solution (ρ,u,φ)on [0,1]×[0,T].

Remark 1.1In this paper, the initial density is assumed to be connected to a vacuum with discontinuities.Although in[20]the initial density is connected to a vacuum continuously,the formη(ρ)=1+ραcan provide the crucial estimate

With the help of this estimate,the bounds ofφ(x,t)can be derived directly.Then one can derive the bounds ofρ(x,t) and overcome the most important step in the globala prioriestimates.However, the formη(ρ)=ραconsidered in this paper can only supply the estimate

Remark 1.2Observing the relations ofu(x,t) andφ(x,t) in the equations (1.5), the globala prioriestimates and the proof of the uniqueness, we see that the regularity ofφ(x,t)is always one order higher thanu(x,t).Thus we retain this character in the definition of theHi-solution, which is different from [32], and this leads to some difficulties in terms of the induction.Fortunately, becauseρ(x,t) satisfies the transport equation, we can improve its regularity a little with the aid of the regularity ofu(x,t) and solve the problem (Lemma 3.3 Step 3).

The local existence of unique solutions is known from the standard method, based on the Schauder Fixed Point theorem via the operator defined by the linearization of the problem on a small time interval, as in [9].We omit the proof and just state the result here.

Lemma 1.1Suppose that (A1) and (A2) hold.Then there exists a small timeT*＞0 depending only on initial data such that problem (1.5)-(1.7) admits a uniqueH2-solution(ρ,u,φ) on [0,1]×[0,T*].

The structure of the rest of this paper is as follows: in Section 2, the global existence of uniqueH2-solutions to problem (1.5)-(1.7) will be proven by the method of extending the local solutions with respect to time based ona prioriestimates.In Section 3, we establish higher-order estimates by mathematical induction, then obtainH2m(m ∈N)-solutions andC∞-solutions.

2 Proof of Theorem 1.1

In this section, we will provide somea prioriestimates of theH2-solutions to (1.5)-(1.7),which enables us to extend the local solution to a global one.First,we give the energy estimate.

Then, by using Gr¨onwall’s inequality and (2.1), we arrive at (2.5).□

In what follows, we deal with the lower bound ofρand the bounds ofφ.This is the key lemma of this section.

Lemma 2.4It holds that

This completes the proof of Lemma 2.4.□

The rest lemmas are about higher order estimates for (ρ,u,φ).

Lemma 2.5For any 0≤t ≤T, the following inequality holds:

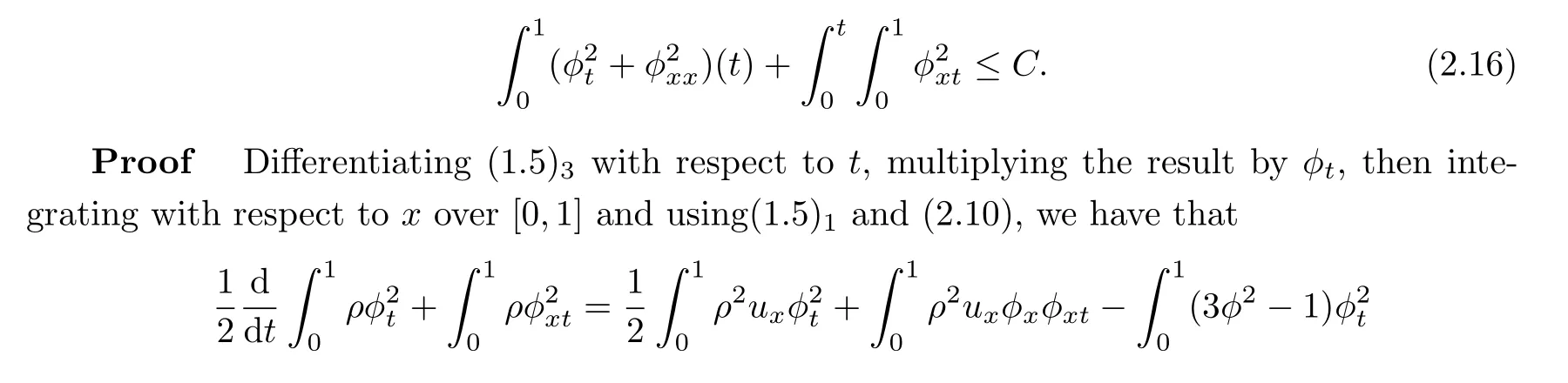
From (1.5)2, by using the above inequality and (2.1), (2.2), (2.7) and (2.16), we have that

Proof From (1.5)1, we see that

This, together with (1.5)3, yields (2.22).The proof of Lemma 2.8 is complete.□

Proof of Theorem 1.1Based on the local existence Lemma 1.1 and Lemmas 2.1 to 2.8,we can finish the proof the existence of theH2-solutions to problem (1.5)-(1.7) by standard procedure.It remains for us to prove the uniqueness of the solution.

Multiplying the above equation byφ1-φ2, integrating over [0,1], and integrating by parts,yields that

The proof of uniqueness is complete.□

3 Proof of Theorem 1.2 and Theorem 1.3

In this section, we will prove Theorems 1.2 and 1.3 by establishing somea prioriestimates.First, by virtue of the estimates in Section 2, we obtain the following lemma:

Lemma 3.1For any 0≤t ≤T, theH2-solution (ρ,u,φ) to the problem (1.5)-(1.7)satisfies that

ProofForm= 1,2, (3.1) has been achieved in Lemmas 3.1 and 3.2.Now we suppose that (3.1) is valid for all 1≤m ≤M-1, and we will prove that (3.1) is also valid form=M.

Step 1We prove that

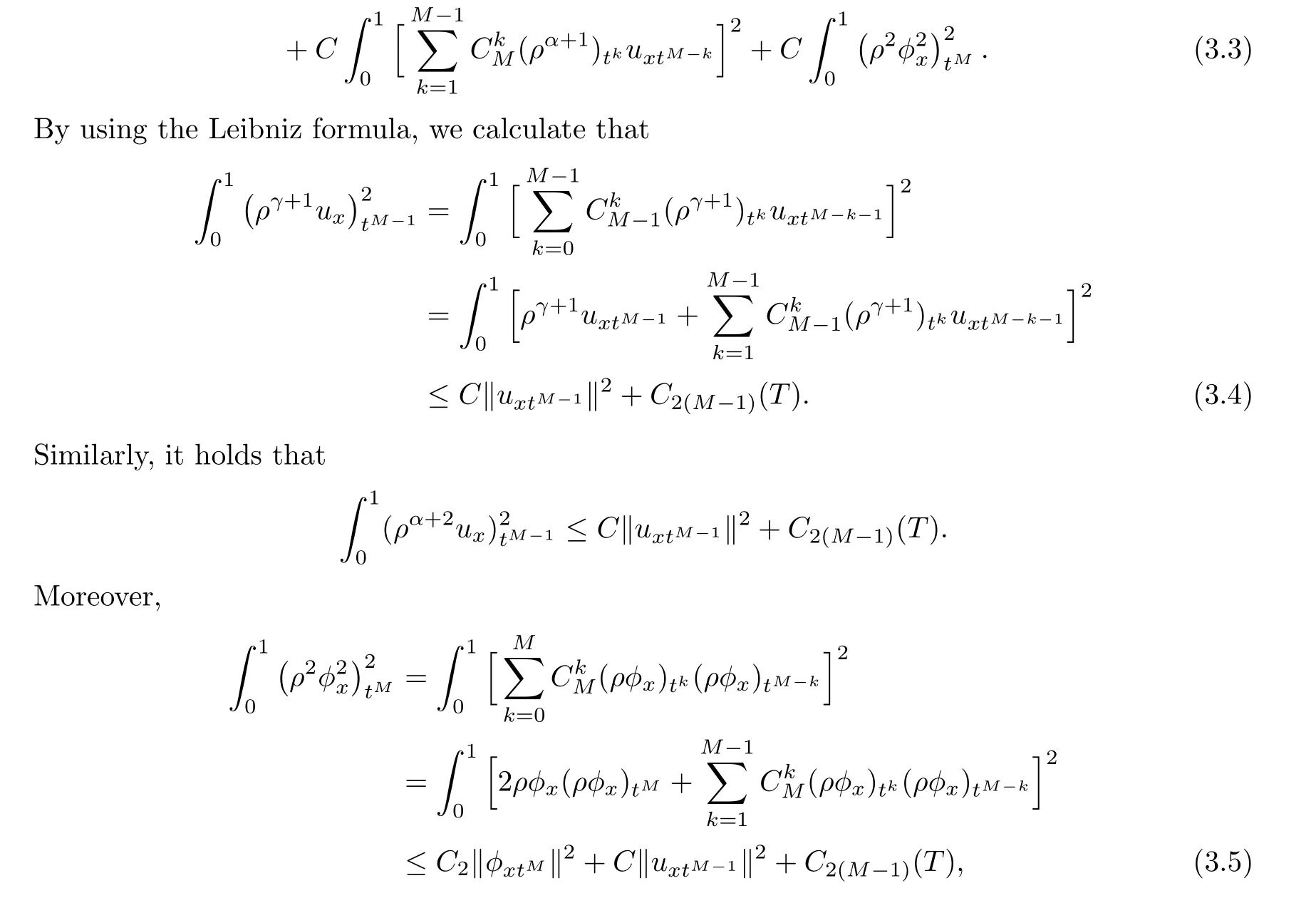
where we have used that

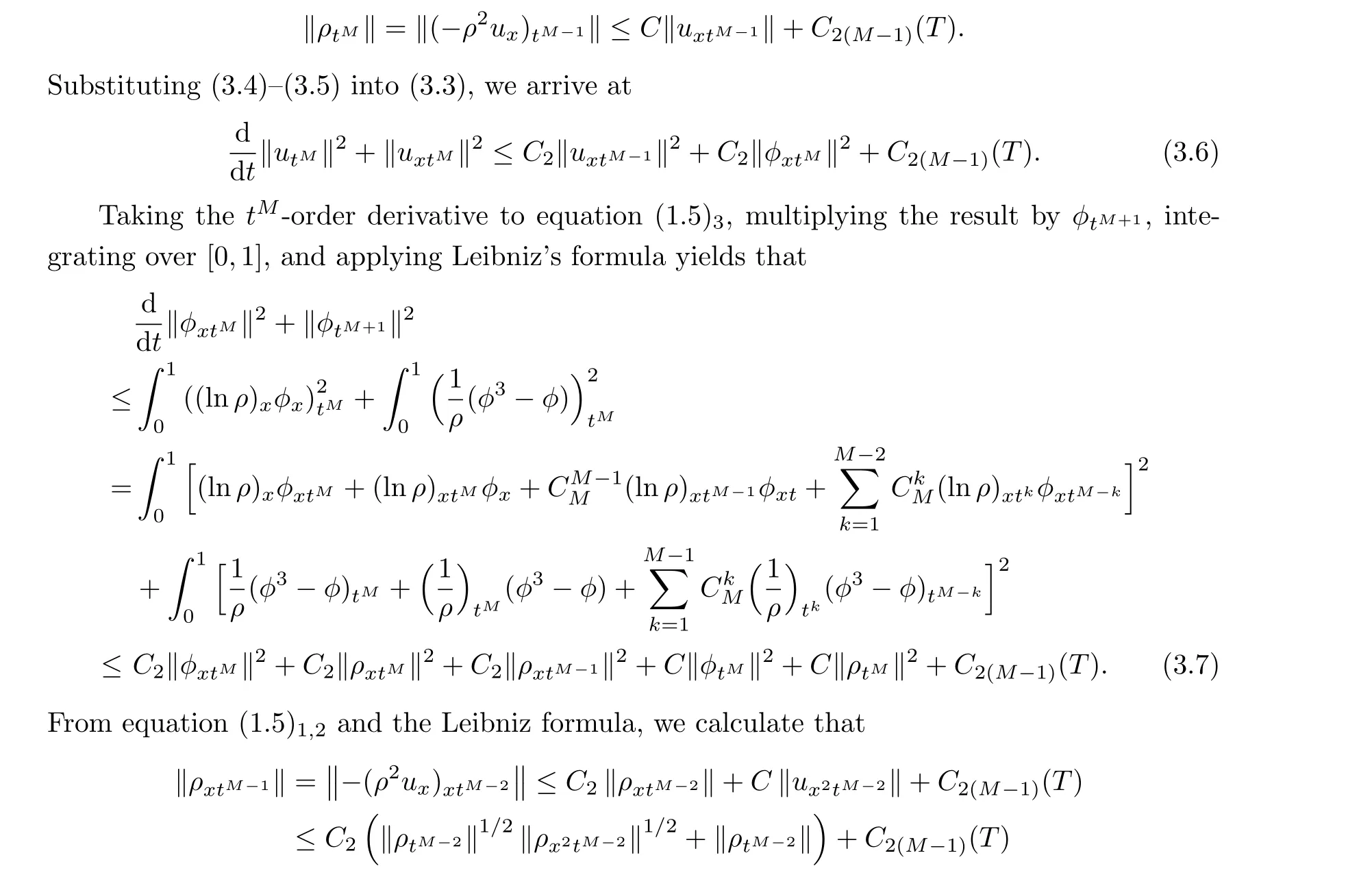
Proof of Theorem 1.2Applying Lemmas 3.1-3.4 and the interpolation inequality readily proves the theorem.□

Proof of Theorem 1.3The embedding theorem easily proves the theorem.□

Conflict of InterestThe authors declare no conflict of interest.